9.1.1 Einführung
Will man Objekte, wie Geraden oder Kreise, die in Kapitel 5 rein geometrisch betrachtet wurden, auch algebraisch (das heißt mit Hilfe von Gleichungen) untersuchen, so muss man zur eindeutigen Beschreibung von Punkten in der Ebene Koordinatensysteme einführen. Die grundlegende Idee von Koordinatensystemen ist sehr einfach: Will man den Ort eines Punktes von Interesse exakt angeben, so braucht man neben einem Referenzpunkt (in der Mathematik als Ursprung bezeichnet) eine bestimmte Längeneinheit (zum Beispiel Kilometer). Dann kann man den Ort des Punktes mit Hilfe von zwei Zahlen eindeutig benennen. Diese zwei Zahlen werden in der Mathematik als Koordinaten des Punktes bezeichnet. In der Praxis findet man dies zum Beispiel auf Schildern, die den Ort von Hydranten im Boden angeben:

In diesem Fall ist der Ursprung der Ort, an dem das Schild angebracht ist, die Längeneinheit ist Meter, und die beiden abzulesenden Zahlen
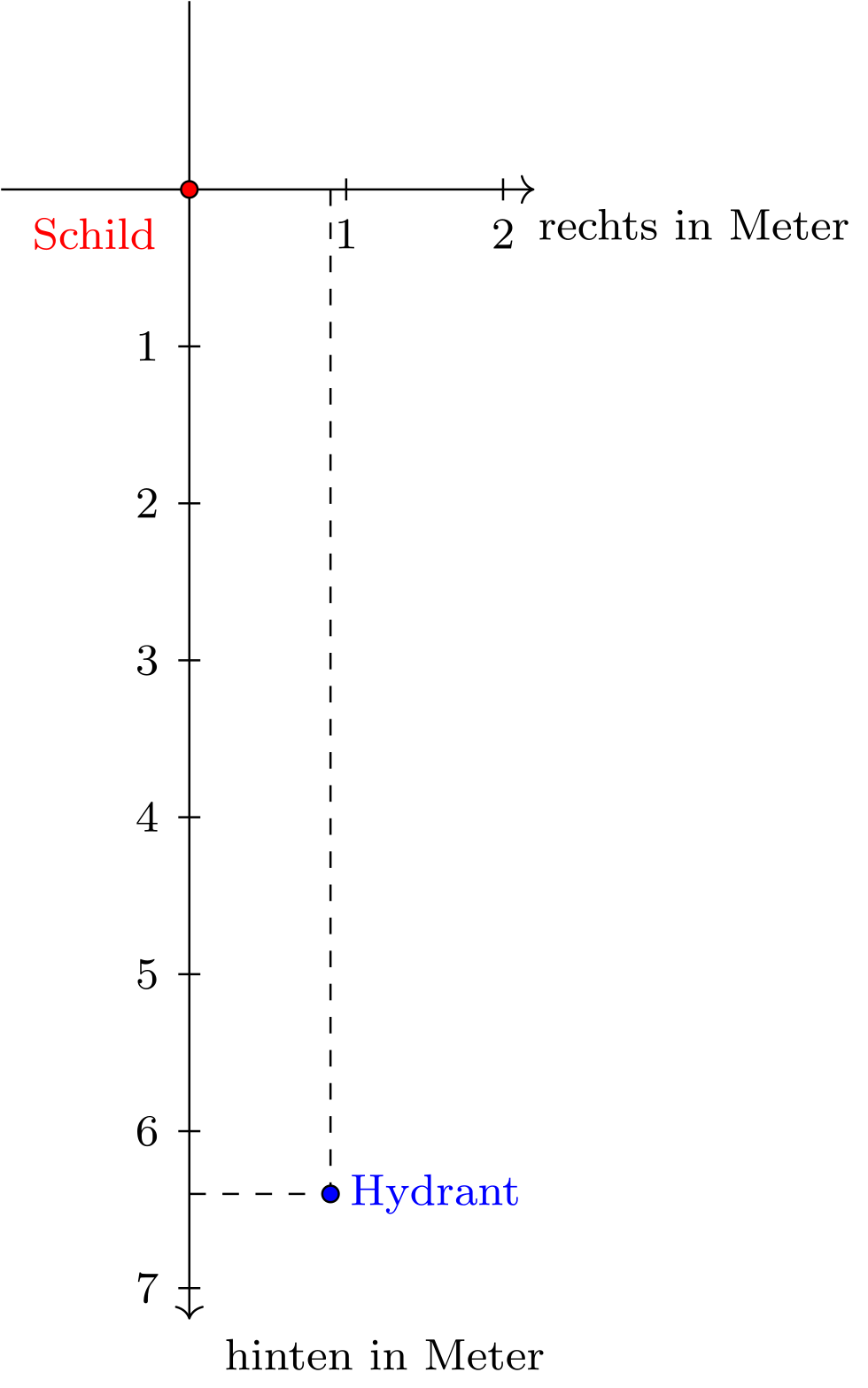
Abbildung 9.1.2: Skizze (C)
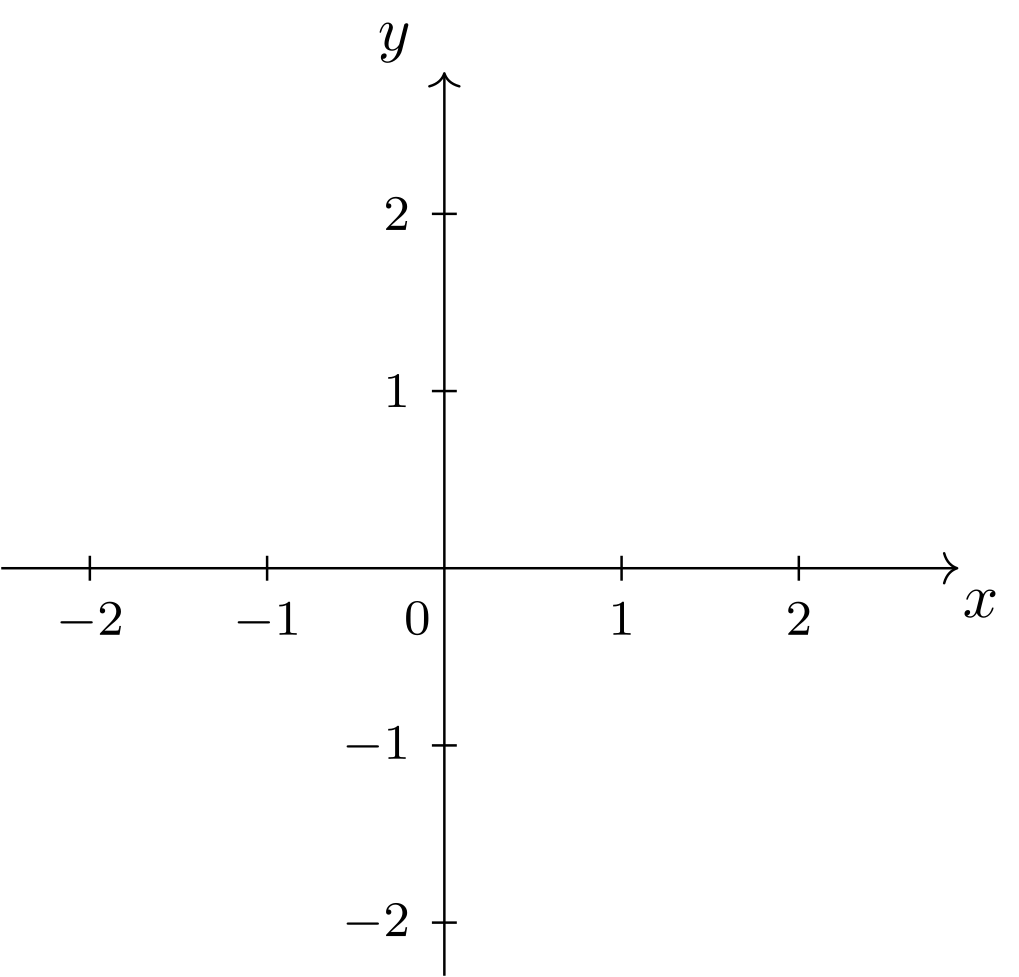
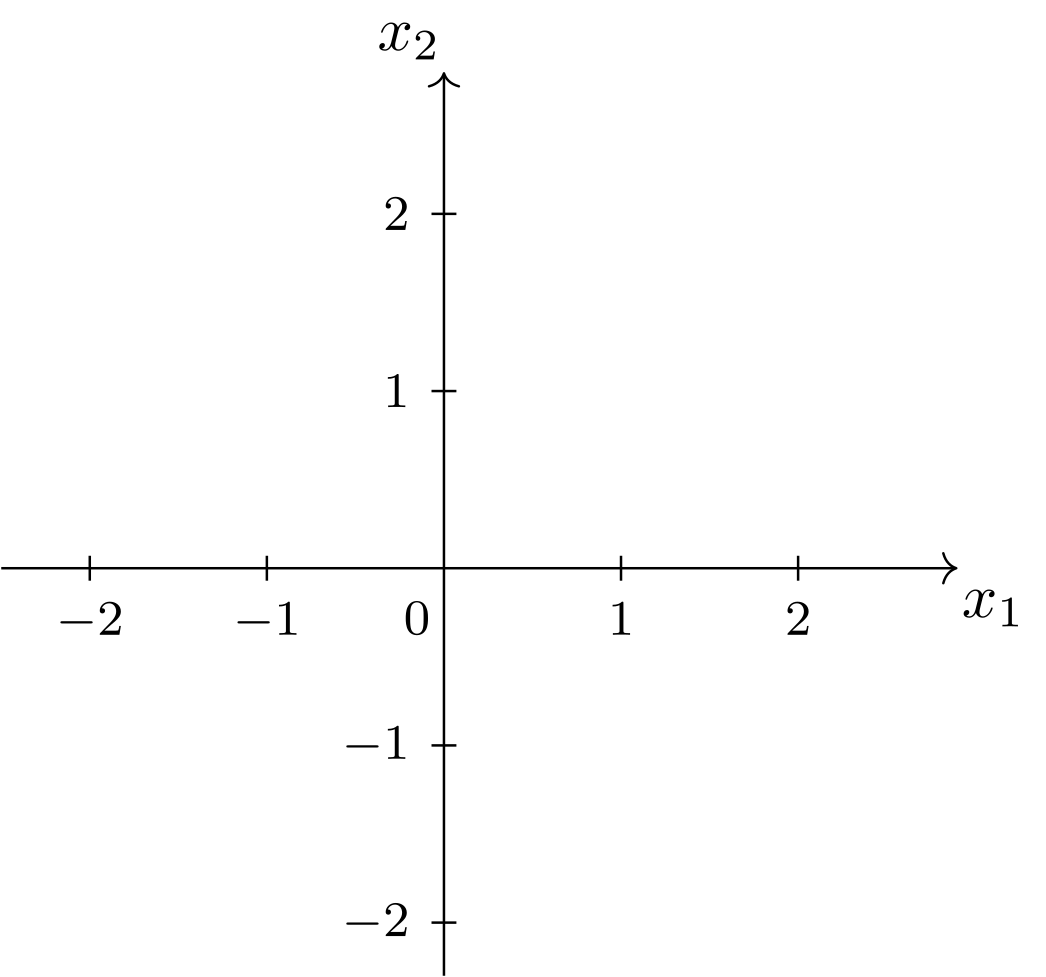
In der Mathematik werden die Richtungen in einem Koordinatensystem selten „rechts“ und „hinten“ genannt. Zeichnet man ein Koordinatensystem, so nennt man die horizontale Richtung oft -Richtung oder -Richtung und die vertikale Richtung -Richtung oder -Richtung. Die mathematische Konvention dabei ist außerdem, dass die Richtungen nach rechts und nach oben verlaufen sollen:
Die verwendete Längeneinheit kann hier noch zusätzlich angegeben werden, diese ist aber für rein mathematische Betrachtungen zunächst nicht wichtig. Beachtet werden sollte aber die Benutzung negativer Koordinaten „links“ und „unterhalb“ des Ursprungs. Die gezeichneten Achsen bezeichnet man schließlich entsprechend oft als -Achse oder -Achse und -Achse oder -Achse. Üblich sind weiterhin die Bezeichnungen Abszissenachse für die horizontale Achse (die Koordinatenwerte darauf heißen dann Abszissen) und Ordinatenachse für die vertikale Achse (die Koordinatenwerte darauf heißen dann Ordinaten).
Man erkennt nun, dass ein solches Koordinatensystem die Ebene in vier Bereiche teilt, die wiederum besondere Bezeichnungen tragen. Man spricht hier von den Quadranten I bis IV:

Abbildung 9.1.5: Skizze (C)
Weiterhin werden die oben beschriebenen Koordinatensysteme auch als kartesische Koordinatensysteme bezeichnet, da ihre Achsen senkrecht aufeinander stehen, sich also im Ursprung unter einem -Winkel schneiden. Es gibt also auch nicht-kartesische Koordinatensysteme, die in diesem Kurs allerdings nicht betrachtet werden. Deshalb wird im Folgenden oft einfach nur der Begriff Koordinatensystem für ein kartesisches Koordinatensystem benutzt.
Hat man nun das Konzept der Koordinatensysteme der Ebene verinnerlicht, so wird klar, dass man auf ähnliche Weise auch die Position von Punkten im Raum beschreiben kann. Will man zum Beispiel die Position eines Flugzeugs exakt angeben, ist dafür nicht nur seine Position relativ zum Tower relevant, sondern auch seine Flughöhe. Man braucht hierfür also eine dritte Koordinate und folglich ein Koordinatensystem mit drei Achsen. Solche Koordinatensysteme werden in Kapitel 10 eingeführt.