6.5.3 Kosinus und Tangens
Im Grunde genommen müssen wir für Kosinus- und Tangensfunktion die zur Sinusfunktion analogen Überlegungen
angehen, die wir aus dem vorigen Unterabschnitt 6.5.2 kennen. Da wir schon etwas Übung besitzen, können wir die
Diskussion etwas straffen. Beginnen wir mit der Kosinusfunktion und betrachten erneut unsere dem Einheitskreis
einbeschriebenen Dreiecke:
Wiederum besitzen alle Hypotenusen dieser so konstruierten rechtwinkligen Dreiecke die Länge , sodass die Kosinus der Winkel im Bild als Längen der Strecken auftreten. Bewegen wir wie zuvor den Punkt im Gegenuhrzeigersinn gleichmäßig um den Kreis und variieren so den Winkel , erhalten wir letztlich die Kosinusfunktion:
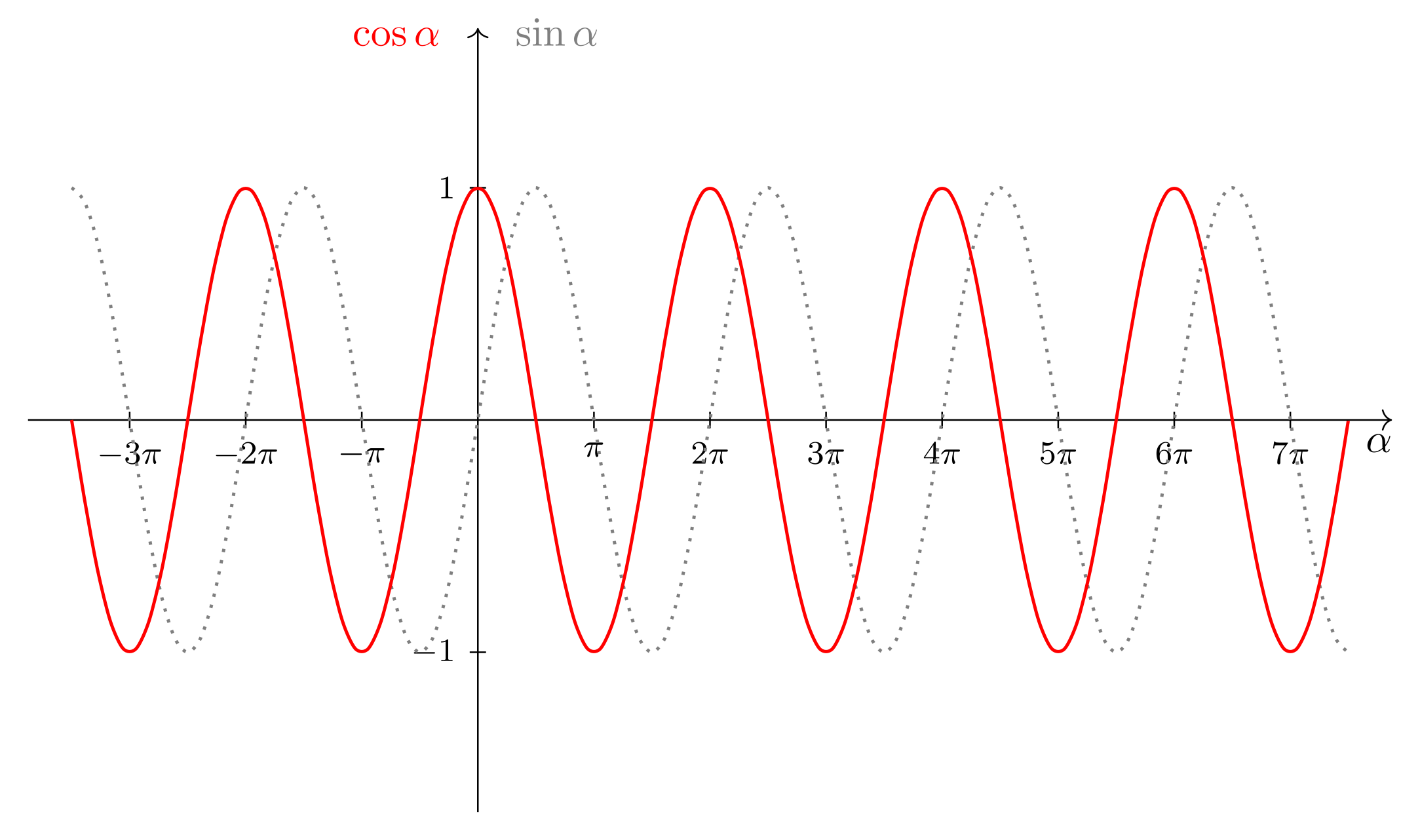
Das Schaubild gibt neben dem Graphen der Kosinus- (durchgezogene Linie) nochmals denjenigen der Sinusfunktion (gepunktete Linie)
zu Vergleichszwecken wieder; wir erkennen eine sehr enge Verwandtschaft, die wir noch thematisieren werden.
Welche wichtigen Eigenschaften besitzt die Kosinusfunktion?
Wiederum besitzen alle Hypotenusen dieser so konstruierten rechtwinkligen Dreiecke die Länge , sodass die Kosinus der Winkel im Bild als Längen der Strecken auftreten. Bewegen wir wie zuvor den Punkt im Gegenuhrzeigersinn gleichmäßig um den Kreis und variieren so den Winkel , erhalten wir letztlich die Kosinusfunktion:

Abbildung 6.5.2: Skizze (C)
Welche wichtigen Eigenschaften besitzt die Kosinusfunktion?
- Die Kosinusfunktion ist ebenfalls eine periodische Funktion. Die Periode ist wieder bzw. .
- Der Definitionsbereich der Kosinusfunktion ist ganz , , der Wertebereich das Intervall von bis
, die Endpunkte inbegriffen, .
- Aus dem obigen Bild der Graphen von und ergibt sich unmittelbar, dass
für alle reellen Werte von gilt. Ebenso richtig, aber etwas schwieriger einzusehen, ist
Wie im Falle des Sinus gibt es auch für den Kosinus eine allgemeine Kosinusfunktion, in deren Definition
zusätzliche Freiheiten in Form von Parametern auftauchen (Amplitudenfaktor , Frequenzfaktor sowie
Verschiebekonstante ); auf diese Art und Weise eröffnet sich wiederum die Möglichkeit, den Funktionsverlauf an
unterschiedliche Situationen (in Anwendungsbeispielen) anzupassen:
Aufgabe 6.5.3
In Beispiel 6.5.1 haben wir das Fadenpendel andiskutiert. Insbesondere kann man den zeitlichen Verlauf der Pendelauslenkung unter den Voraussetzungen bestimmen, dass die Schwingungsdauer gerade Sekunden beträgt, und dass zum Zeitpunkt das Pendel bei einer Auslenkung von losgelassen wird:
Kann man diese Situation auch mit Hilfe der (allgemeinen) Kosinusfunktion (anstelle der Sinusfunktion) beschreiben, und wenn ja, wie sieht dann aus?
In Beispiel 6.5.1 haben wir das Fadenpendel andiskutiert. Insbesondere kann man den zeitlichen Verlauf der Pendelauslenkung unter den Voraussetzungen bestimmen, dass die Schwingungsdauer gerade Sekunden beträgt, und dass zum Zeitpunkt das Pendel bei einer Auslenkung von losgelassen wird:
Kann man diese Situation auch mit Hilfe der (allgemeinen) Kosinusfunktion (anstelle der Sinusfunktion) beschreiben, und wenn ja, wie sieht dann aus?
Der Tangens ist gegeben als das Verhältnis von Sinus zu Kosinus. Damit ist sofort klar, dass die Tangensfunktion nicht auf allen reellen Zahlen definiert sein kann, denn schließlich besitzt die Kosinusfunktion unendliche viele Nullstellen, wie man z.B. in Aufgabe 6.5.2 sehen kann. In Aufgabe 6.5.2 wird auch die Lage der Nullstellen von bestimmt (); demzufolge ist der Definitionsbereich der Tangensfunktion .
Und wie sieht es mit dem Wertebereich aus? Bei den -Nullstellen wird die Tangensfunktion gegen positiv bzw. negativ unendliche Werte streben und Polstellen haben und bei den -Nullstellen wird Null. Dazwischen sind alle reellen Werte möglich, daher ist . Insgesamt ergibt sich für den Graphen der Tangensfunktion
folgendes Bild:
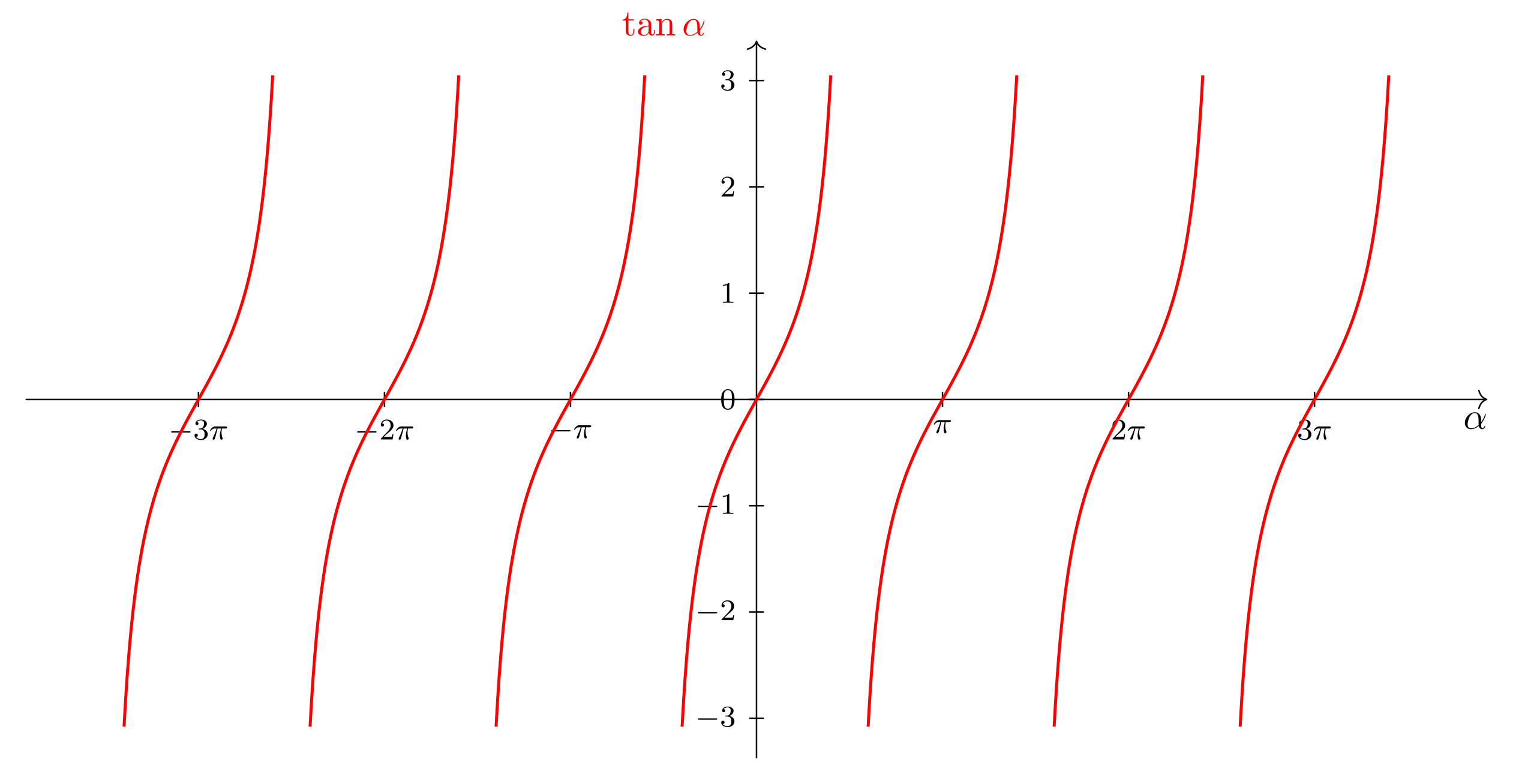
Abbildung 6.5.3: Skizze (C)
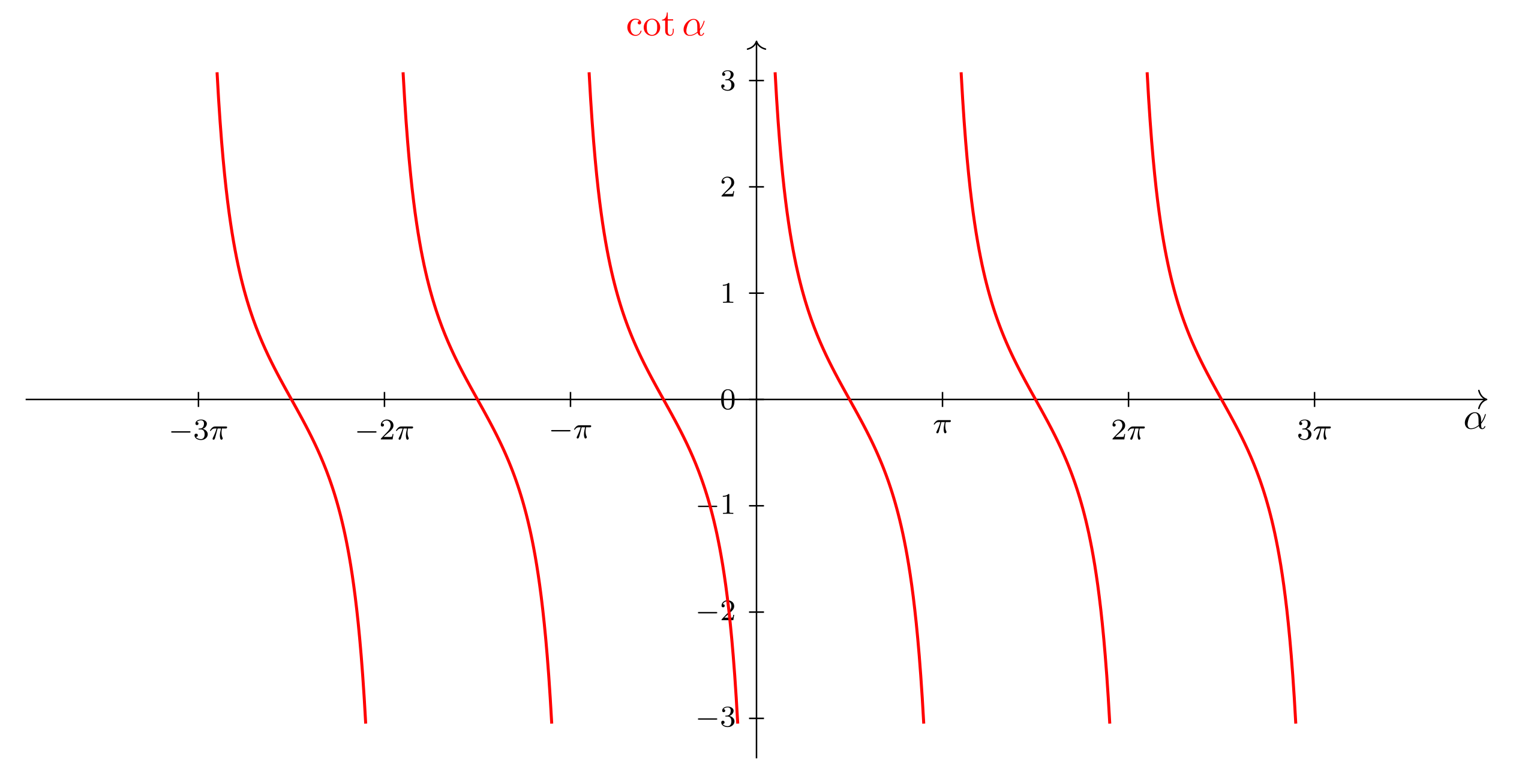
Aufgabe 6.5.4
Der sogenannte Kotangens (Abkürzung ) ist definiert durch .
Geben Sie Definitions- und Wertebereich der Kotangensfunktion an!
Der sogenannte Kotangens (Abkürzung ) ist definiert durch .
Geben Sie Definitions- und Wertebereich der Kotangensfunktion an!