4.2.1 Einführung
Man beschränkt sich zunächst auf Lineare Gleichungssysteme in zwei
Unbekannten.
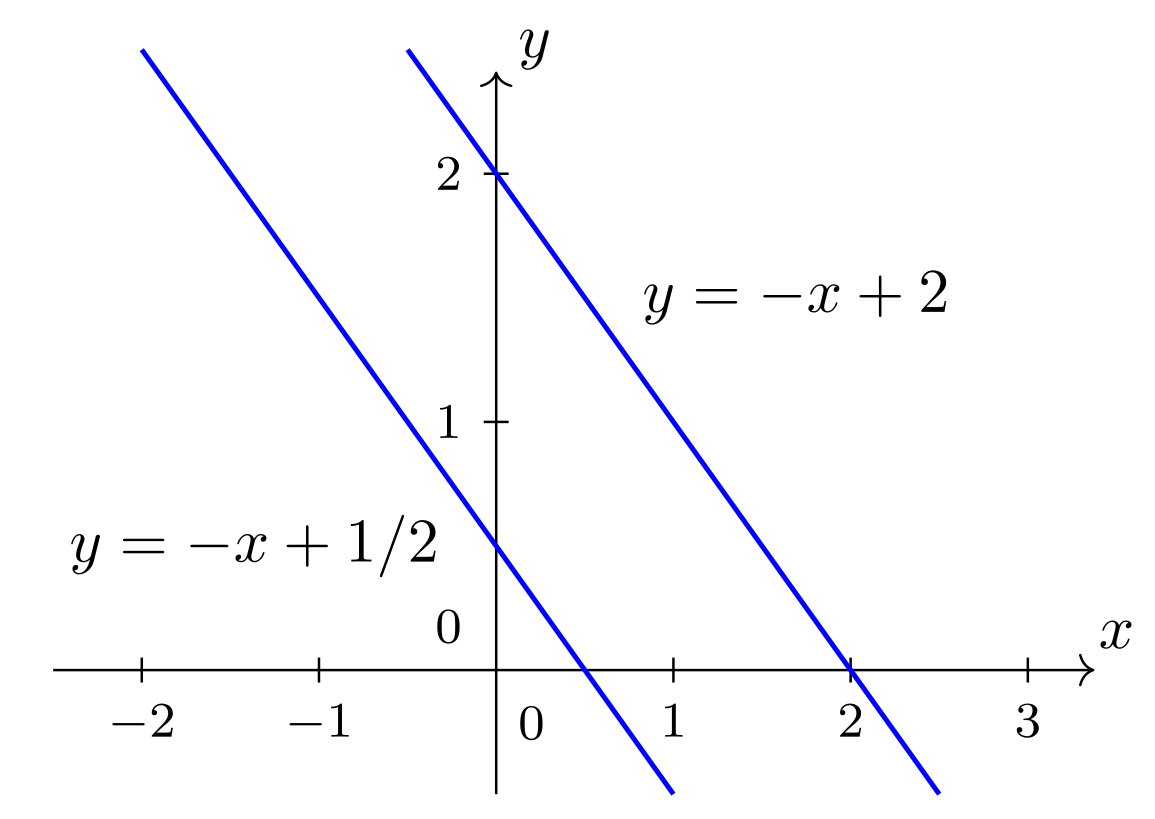
Aufgrund der Linearität kann jede der beiden Gleichungen des Systems in Infobox 4.2.1 für sich als Gleichung einer Geraden in der --Ebene interpretiert werden: Löst man z.B. die erste Gleichung nach auf,
so kann man aus dieser expliziten Form direkt ablesen, dass eine Gerade mit der Steigung und dem -Achsenabschnitt beschrieben wird.
Am Rande wird festgehalten, dass das eben erwähnte Freistellen nach natürlich nur funktioniert, falls ist. Ist , so lautet die erste Gleichung ; diese ist für äquivalent zu , was bedeutet, dass einen konstanten Wert annimmt; dies stellt ebenfalls eine Gerade dar, nämlich eine Gerade parallel zur -Achse im Abstand .
Und was, wenn sowohl als auch gilt? Nun, dann muss ebenfalls sein, da ansonsten die erste Gleichung von vornherein einen Widerspruch ergeben würde. Für ist aber die erste Gleichung (für alle Werte von und ) immer identisch erfüllt () und somit wertlos.
Im Fall der zweiten Gleichung in Infobox 4.2.1 geht man ganz entsprechend vor:
Insgesamt erhält man zwei Geraden als Repräsentanten der beiden linearen Gleichungen, und die Frage nach Lösbarkeit und Lösung des Linearen Gleichungssystems, also die Frage nach der gleichzeitigen Gültigkeit beider Gleichungen, liest sich als Frage nach Existenz und Lage des Schnittpunkts der beiden Geraden. Dazu schaut man sich ein konkretes Beispiel an:
Diese anschauliche Betrachtungsweise eignet sich hervorragend, alle Fälle zu
diskutieren, die überhaupt nur auftreten können: Denn entweder schneiden sich zwei Geraden in der --Ebene -
und dann ist der Schnittpunkt zwangsläufig eindeutig -, oder aber zwei solche Geraden verlaufen parallel -
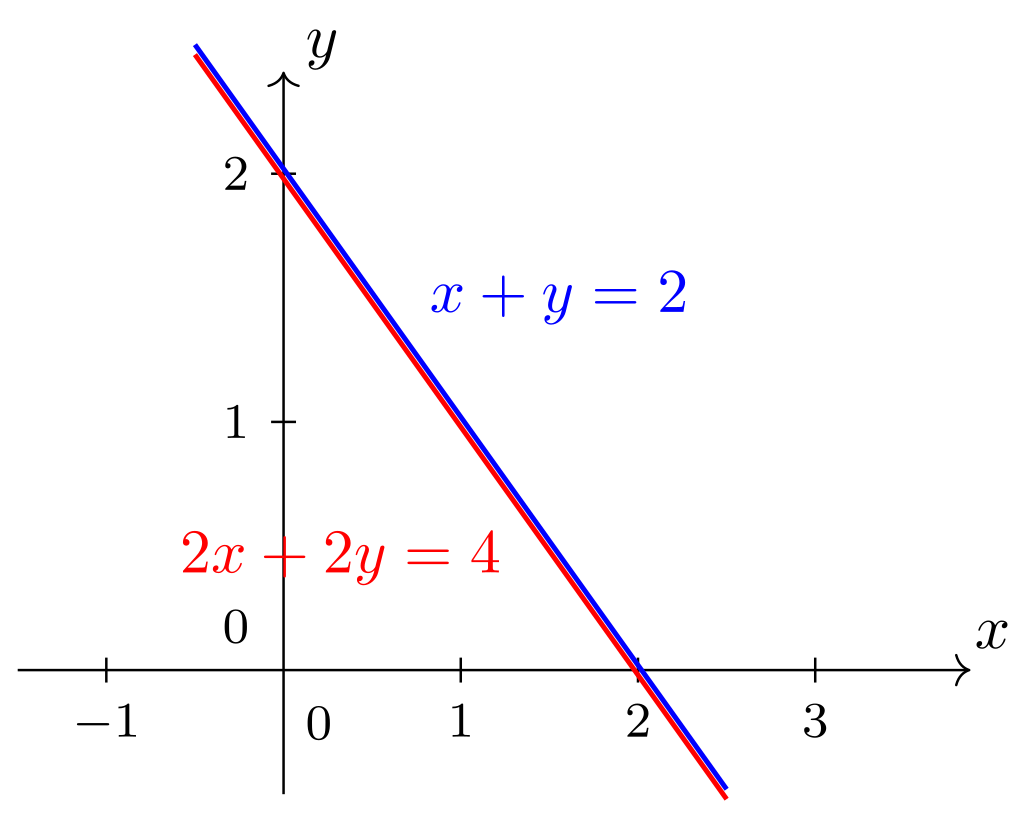
und besitzen somit keinen Schnittpunkt -, oder aber die beiden Geraden sind deckungsgleich -
und schneiden sich daher sozusagen in unendlich vielen Punkten. Andere Möglichkeiten sind nicht denkbar.
Demzufolge kann man im Hinblick auf die Mächtigkeit der Lösungsmenge des
zugehörigen linearen Gleichungssystems Folgendes festhalten:
Das Gesagte soll an zwei weiteren Beispielen, bei denen man direkt mit den
Linearen Gleichungssystemen startet, verdeutlicht werden:
Im Falle des Beispiels in der rechten Spalte sind andere Parametrisierungen der Lösungsmenge möglich und
erlaubt. Es kommt im Grunde nur darauf an, die Punkte der (deckungsgleichen) Geraden geeignet zu beschreiben.
Bei der obigen Angabe von wurde einfach die Geradengleichung selbst verwendet und die
Laufvariable statt genannt.
Und was hat es mit den oben erwähnten möglichen Einschränkungen wegen der Grundmenge auf sich? Auch hierzu ein Beispiel:
Info
4.2.1
Allgemein hat ein Lineares Gleichungssystem (LGS), bestehend aus zwei Gleichungen in den Unbekannten und , folgende Gestalt:
Dabei sind und die sogenannten Koeffizienten des Linearen Gleichungssystems, die ebenso wie die rechten Seiten und der Gleichungen meist aus den reellen Zahlen stammen und aufgrund der Problemstellung (weitgehend) vorgegeben sind.
Sind die rechten Seiten und beide gleich (), so spricht man von einem homogenen, andernfalls von einem inhomogenen Linearen Gleichungssystem.
Allgemein hat ein Lineares Gleichungssystem (LGS), bestehend aus zwei Gleichungen in den Unbekannten und , folgende Gestalt:
Dabei sind und die sogenannten Koeffizienten des Linearen Gleichungssystems, die ebenso wie die rechten Seiten und der Gleichungen meist aus den reellen Zahlen stammen und aufgrund der Problemstellung (weitgehend) vorgegeben sind.
Sind die rechten Seiten und beide gleich (), so spricht man von einem homogenen, andernfalls von einem inhomogenen Linearen Gleichungssystem.
Aufgrund der Linearität kann jede der beiden Gleichungen des Systems in Infobox 4.2.1 für sich als Gleichung einer Geraden in der --Ebene interpretiert werden: Löst man z.B. die erste Gleichung nach auf,
so kann man aus dieser expliziten Form direkt ablesen, dass eine Gerade mit der Steigung und dem -Achsenabschnitt beschrieben wird.
Am Rande wird festgehalten, dass das eben erwähnte Freistellen nach natürlich nur funktioniert, falls ist. Ist , so lautet die erste Gleichung ; diese ist für äquivalent zu , was bedeutet, dass einen konstanten Wert annimmt; dies stellt ebenfalls eine Gerade dar, nämlich eine Gerade parallel zur -Achse im Abstand .
Und was, wenn sowohl als auch gilt? Nun, dann muss ebenfalls sein, da ansonsten die erste Gleichung von vornherein einen Widerspruch ergeben würde. Für ist aber die erste Gleichung (für alle Werte von und ) immer identisch erfüllt () und somit wertlos.
Im Fall der zweiten Gleichung in Infobox 4.2.1 geht man ganz entsprechend vor:
Insgesamt erhält man zwei Geraden als Repräsentanten der beiden linearen Gleichungen, und die Frage nach Lösbarkeit und Lösung des Linearen Gleichungssystems, also die Frage nach der gleichzeitigen Gültigkeit beider Gleichungen, liest sich als Frage nach Existenz und Lage des Schnittpunkts der beiden Geraden. Dazu schaut man sich ein konkretes Beispiel an:
Beispiel
4.2.2
Das Lineare Gleichungssystem aus dem einführenden Beispiel 4.1.1 lautet:
(Hier nehmen die allgemeinen Koeffizienten und rechten Seiten des Systems 4.2.1 somit die Werte und an.)
Es werden zwei Geraden mit den Steigungen bzw. und den -Achsenabschnitten bzw. beschrieben:
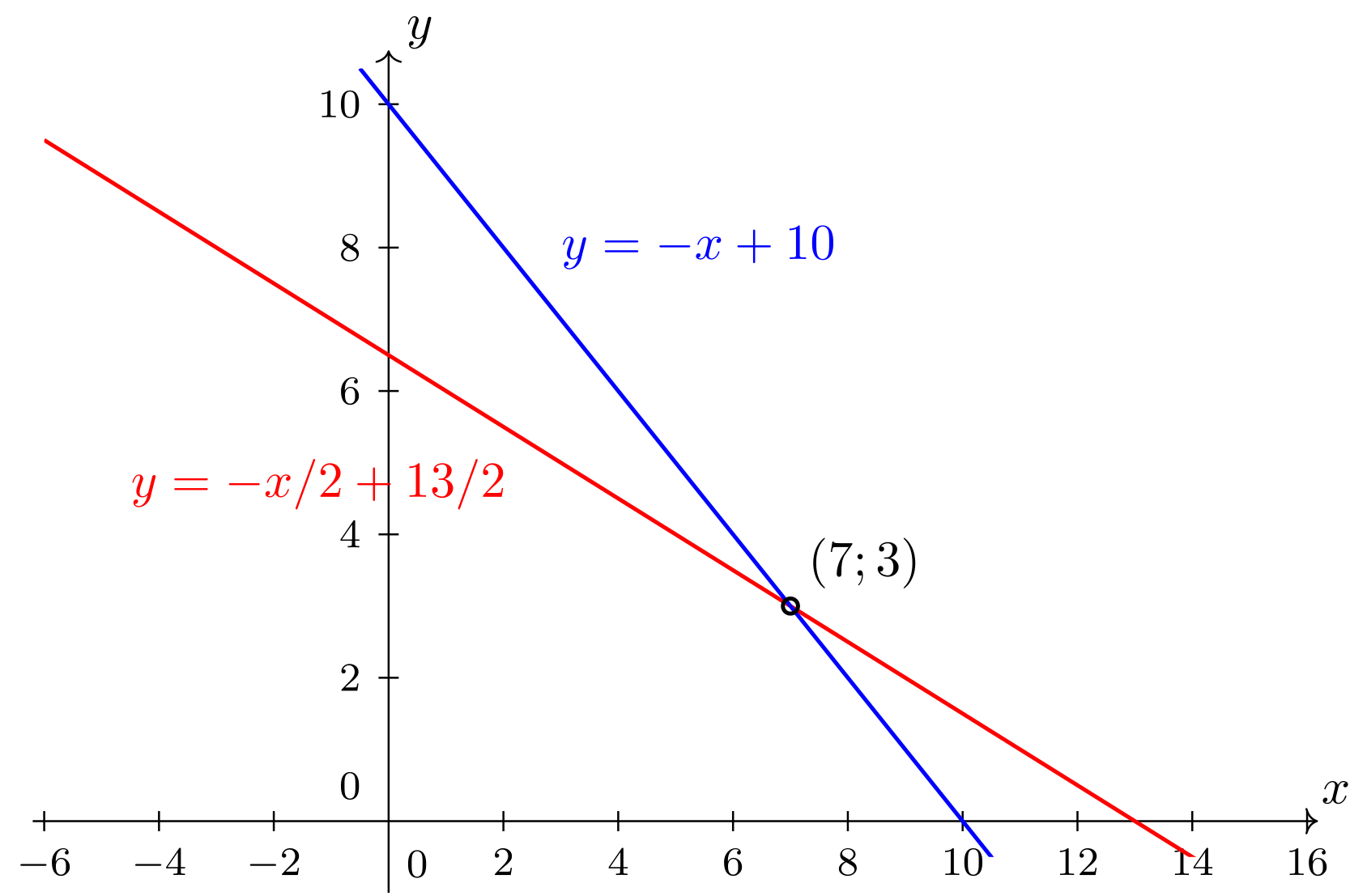
Man erkennt aus dem Schaubild, dass sich die beiden Geraden in der Tat schneiden, und liest
die Koordinaten des Schnittpunktes zu ab. Dementsprechend besitzt
das hier betrachtete Lineare Gleichungssystem eine eindeutige Lösung; die
Lösungsmenge enthält genau ein Zahlenpaar, .
Das Lineare Gleichungssystem aus dem einführenden Beispiel 4.1.1 lautet:
(Hier nehmen die allgemeinen Koeffizienten und rechten Seiten des Systems 4.2.1 somit die Werte und an.)
Es werden zwei Geraden mit den Steigungen bzw. und den -Achsenabschnitten bzw. beschrieben:

Abbildung 4.2.1: Skizze (C)
Info
4.2.3
Ein inhomogenes Lineares Gleichungssystem besitzt entweder eine eindeutige Lösung oder aber keine Lösung oder aber unendlich viele Lösungen.
Ein homogenes Lineares Gleichungssystem weist immer eine Lösung auf, nämlich die sogenannte triviale Lösung und . Darüber hinaus kann ein solches homogenes System auch unendlich viele Lösungen besitzen.
Ein inhomogenes Lineares Gleichungssystem besitzt entweder eine eindeutige Lösung oder aber keine Lösung oder aber unendlich viele Lösungen.
Ein homogenes Lineares Gleichungssystem weist immer eine Lösung auf, nämlich die sogenannte triviale Lösung und . Darüber hinaus kann ein solches homogenes System auch unendlich viele Lösungen besitzen.
Beispiel
4.2.4
In beiden Fällen wählt man als Grundmenge die Menge der reellen Zahlen .
In beiden Fällen wählt man als Grundmenge die Menge der reellen Zahlen .
|
| |||||||||||||
|
| |||||||||||||
|
|
Und was hat es mit den oben erwähnten möglichen Einschränkungen wegen der Grundmenge auf sich? Auch hierzu ein Beispiel:
Beispiel
4.2.5
Auf einem Volksfest verspricht ein besonders pfiffiger Standbesitzer geradezu traumhafte Preise und das gegen einen lächerlich geringen Spieleinsatz, wenn, ja wenn einer der Passanten ihm nur folgendes kleine Rätsel löst: Ich habe mit einem Würfel zweimal gewürfelt. Ziehe ich vom Sechsfachen der zweiten Augenzahl das Zweifache der ersten ab, so erhalte ich die Zahl . Addiere ich andererseits zum Vierfachen der ersten Augenzahl die Zahl , so bekomme ich das Zwölffache der zweiten Augenzahl. Welche beiden Zahlen habe ich gewürfelt?
Bezeichnet man die Augenzahl des ersten Würfelwurfs mit , diejenige des zweiten mit , so kann man die Aussagen des Standbesitzers sehr schnell in Gleichungen übersetzen:
Man stellt fest, dass das entstehende Lineare Gleichungssystem - anschaulich interpretiert - auf zwei deckungsgleiche Geraden führt. Vordergründig scheint es daher unendlich viele Lösungen zu geben.
Hier kommt jetzt allerdings die Grundmenge ins Spiel: Da sowohl als auch Augenzahlen eines Würfels repräsentieren, können beide Unbekannte jeweils nur einen Wert aus der Menge annehmen. Betrachtet man die Gerade in der --Ebene,
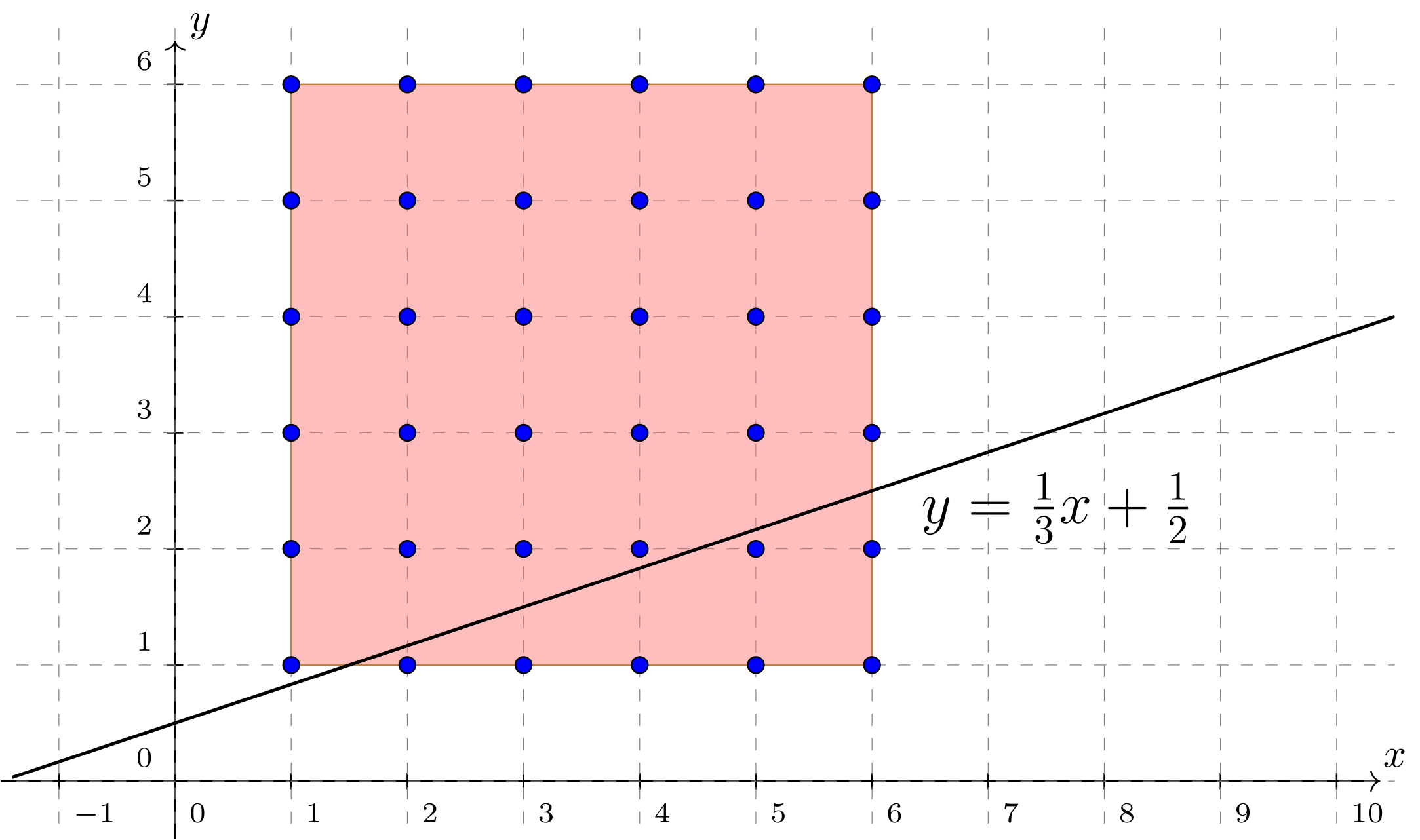
so erkennt man, dass
kein mögliches Augenzahlpaar auf dieser Geraden liegt; daher ist die Lösungsmenge hier tatsächlich leer,
.
Auf einem Volksfest verspricht ein besonders pfiffiger Standbesitzer geradezu traumhafte Preise und das gegen einen lächerlich geringen Spieleinsatz, wenn, ja wenn einer der Passanten ihm nur folgendes kleine Rätsel löst: Ich habe mit einem Würfel zweimal gewürfelt. Ziehe ich vom Sechsfachen der zweiten Augenzahl das Zweifache der ersten ab, so erhalte ich die Zahl . Addiere ich andererseits zum Vierfachen der ersten Augenzahl die Zahl , so bekomme ich das Zwölffache der zweiten Augenzahl. Welche beiden Zahlen habe ich gewürfelt?
Bezeichnet man die Augenzahl des ersten Würfelwurfs mit , diejenige des zweiten mit , so kann man die Aussagen des Standbesitzers sehr schnell in Gleichungen übersetzen:
Man stellt fest, dass das entstehende Lineare Gleichungssystem - anschaulich interpretiert - auf zwei deckungsgleiche Geraden führt. Vordergründig scheint es daher unendlich viele Lösungen zu geben.
Hier kommt jetzt allerdings die Grundmenge ins Spiel: Da sowohl als auch Augenzahlen eines Würfels repräsentieren, können beide Unbekannte jeweils nur einen Wert aus der Menge annehmen. Betrachtet man die Gerade in der --Ebene,

Abbildung 4.2.4: Skizze (C)