6.6.2 Symmetrie
Info
6.6.1
Eine Funktion heißt gerade oder achsensymmetrisch, falls für alle
gilt. Analog heißt die Funktion ungerade oder punktsymmetrisch, falls für alle
gilt.
Eine Funktion heißt gerade oder achsensymmetrisch, falls für alle
gilt. Analog heißt die Funktion ungerade oder punktsymmetrisch, falls für alle
gilt.
Diese beiden Symmetriebedingungen für Funktionen sagen also etwas über das Aussehen ihrer Graphen aus. Bei geraden Funktionen ändert sich der Graph bei Spiegelung an der Hochachse nicht, und bei ungeraden Funktionen ändert sich der Graph bei Spiegelung am Ursprung nicht. Wir listen einige Beispiele auf.
Beispiel
6.6.2
- Die Funktionen
und
also die Standardparabel (vgl. Abschnitt 6.2.6) und die Betragsfunktion (vgl. Abschnitt 6.2.5), sind Beispiele für gerade Funktionen. Es gilt und für alle . Die Graphen weisen die Spiegelsymmetrie an der Hochachse auf:
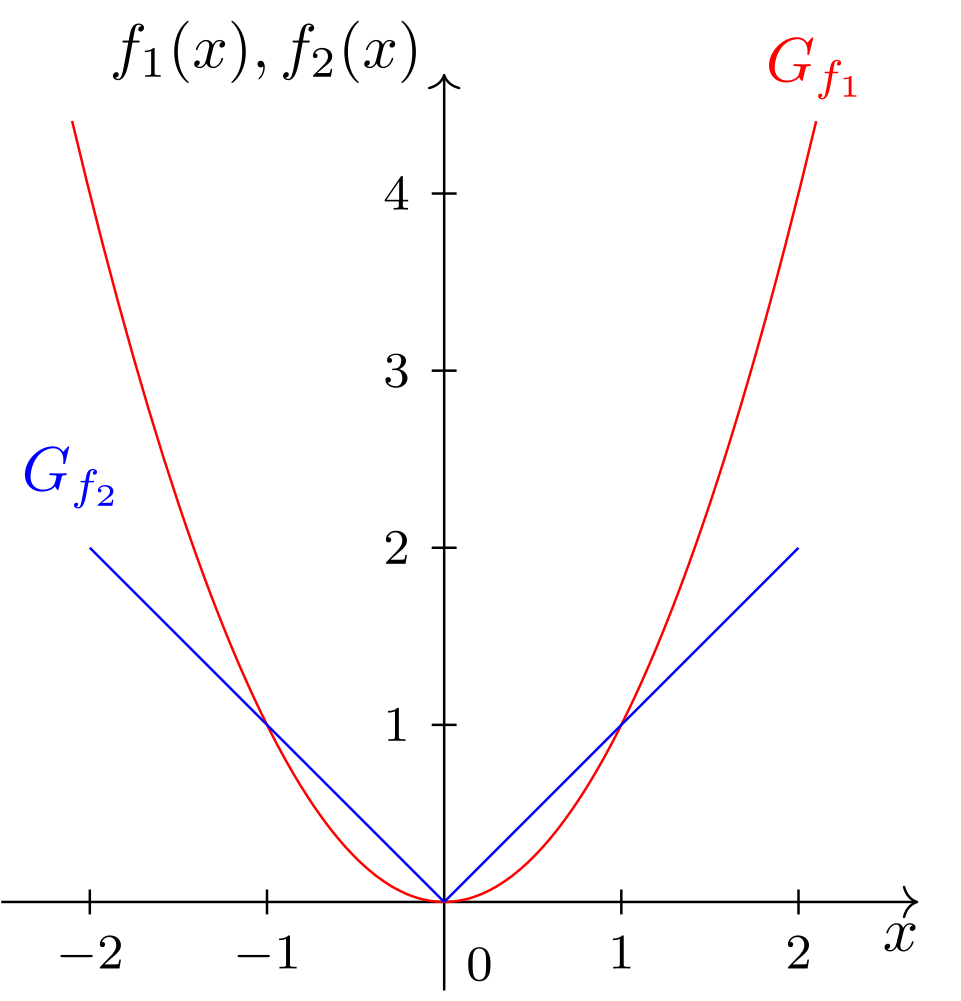Abbildung 6.6.1: Skizze (C)
- Die Funktion
also die kubische Parabel (vgl. Abschnitt 6.2.6), ist ein Beispiel für eine ungerade Funktion. Es gilt für alle . Der Graph ist punktsymmetrisch bezüglich des Ursprungs:
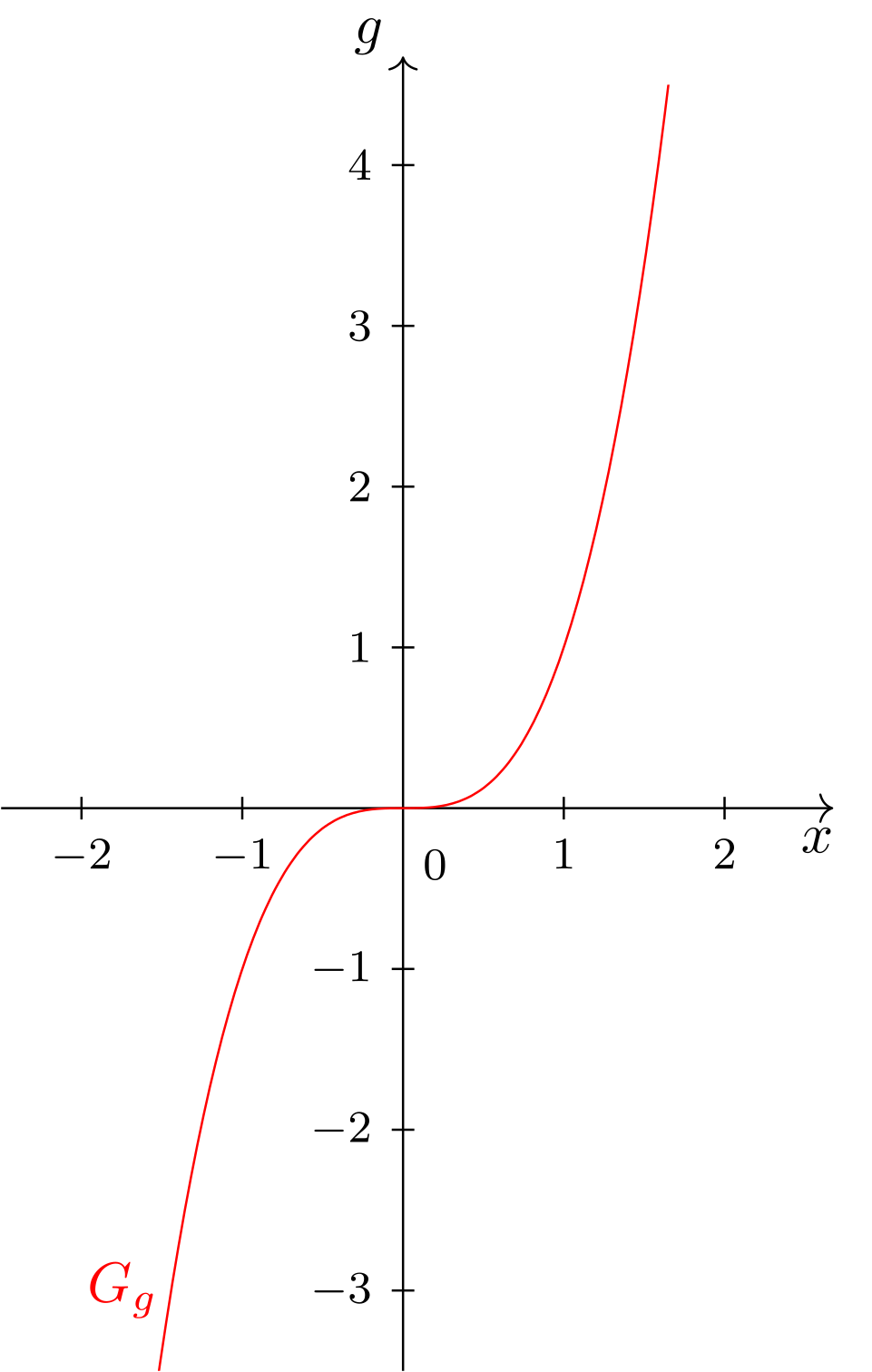Abbildung 6.6.2: Skizze (C)
Natürlich sind die Symmetrieeigenschaften von Funktionen auch benutzbar, wenn der Definitionsbereich der Funktion nicht die gesamten reellen Zahlen umfasst. Es muss dann aber eine Definitionsmenge vorliegen, die die in der Mitte des Intervalls enthält. Ein Beispiel dafür ist die Tangens-Funktion in der Aufgabe unten.
Aufgabe 6.6.3
Geben Sie von den folgenden Funktionen jeweils an, ob diese gerade, ungerade oder nicht-symmetrisch sind.
Geben Sie von den folgenden Funktionen jeweils an, ob diese gerade, ungerade oder nicht-symmetrisch sind.