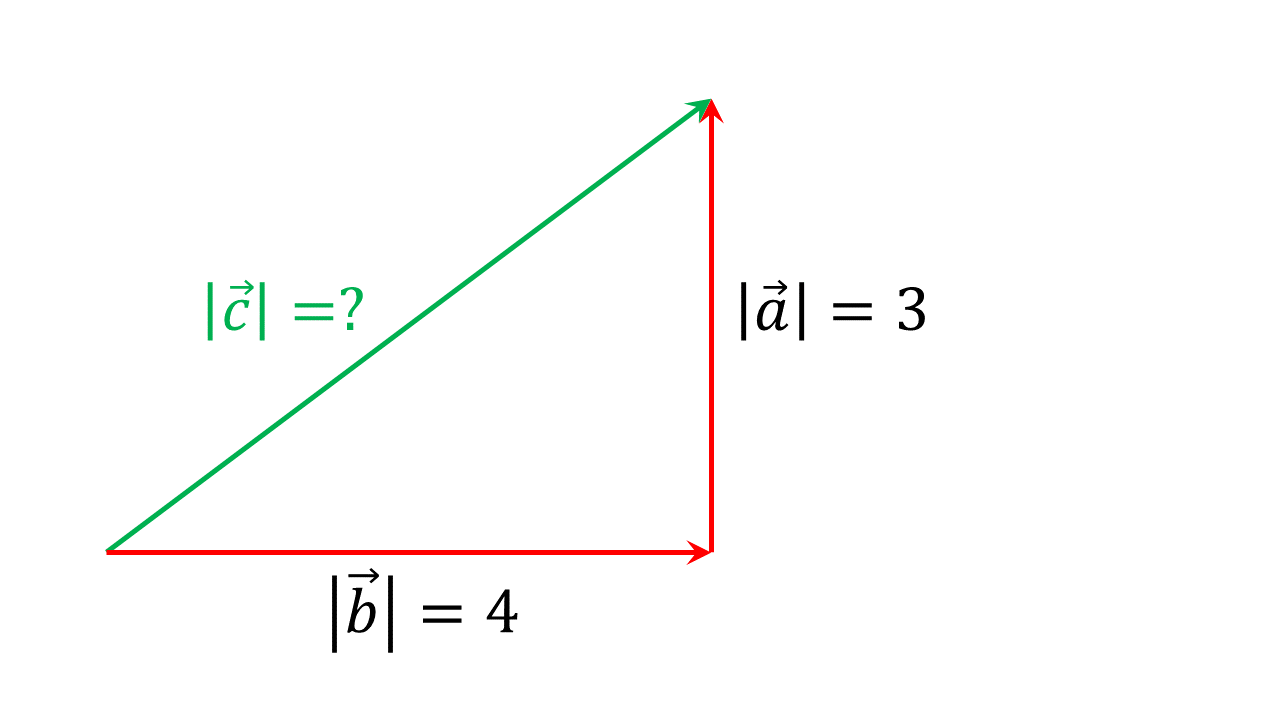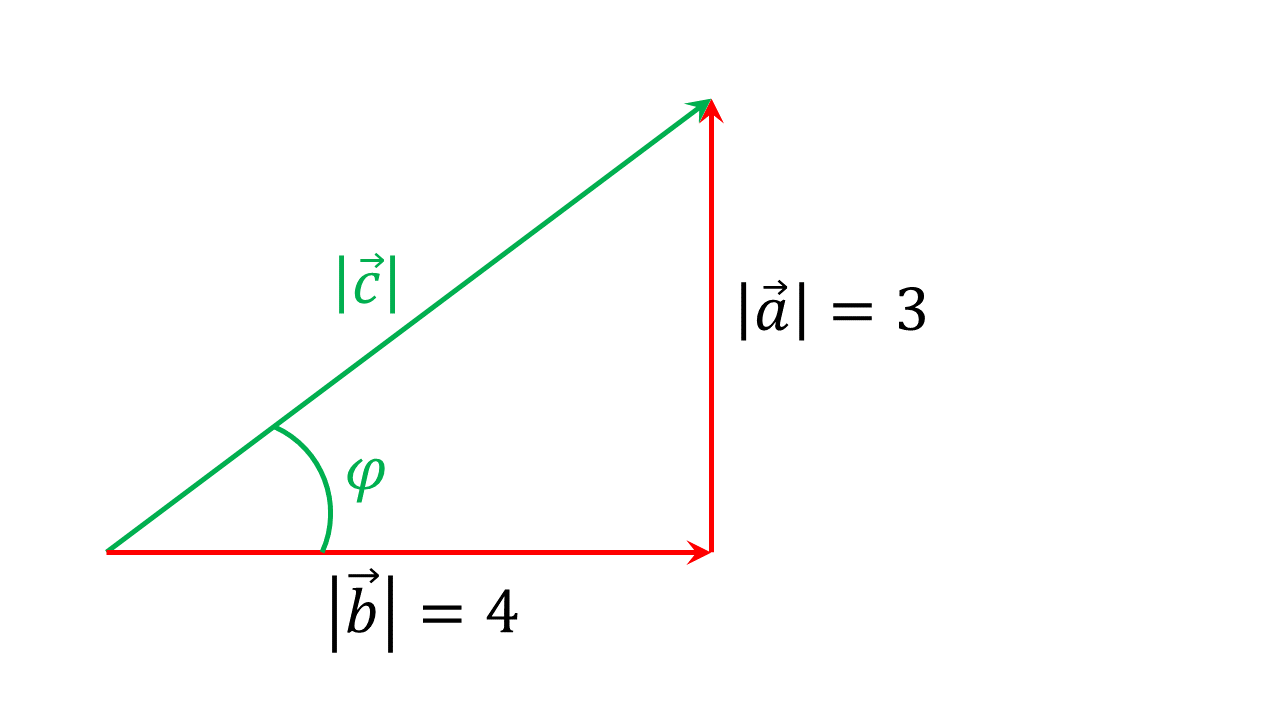3.1.2 Physikalische Vektorgrößen
Basiswissen „Skalare“
Größen, die durch die Angabe eines Zahlenwertes und einer Einheit vollständig beschrieben sind, bezeichnet man als Skalare. Dazu gehören zum Beispiel die Masse oder die Temperatur eines Körpers.
Beispiel
3.1.19
Gießt man in einen Topf mit Wasser noch Wasser hinzu, befinden sich Wasser im Topf: .
Gießt man in einen Topf mit Wasser noch Wasser hinzu, befinden sich Wasser im Topf: .
Beispiel
3.1.20
Entfernt man aus einem --Sack Kartoffeln , bleiben übrig: .
Entfernt man aus einem --Sack Kartoffeln , bleiben übrig: .
Basiswissen „Physikalische Vektorgrößen“
Neben den Skalaren gibt es jedoch auch Größen, die zusätzlich zu einem Zahlenwert und der zugehörigen Einheit noch eine Richtung besitzen, zum Beispiel die Geschwindigkeit eines Körpers oder auch Kräfte. Solche Größen werden als Vektoren bezeichnet. Vektorgrößen werden durch einen Pfeil über dem Buchstaben gekennzeichnet, z.B. , . In manchen Lehrbüchern werden vektorielle Größen auch fett gedruckt.
Anschaulich werden Vektoren in Skizzen durch Pfeile dargestellt. Dabei entspricht die Länge des Pfeils dem Betrag der Größe und die Richtung des Pfeils weist in die Richtung der Größe. Skizziert man ein fahrendes Auto, zeigt der Pfeil in die Richtung, in die das Auto fährt, und die Länge des Pfeils entspricht dem Betrag seiner Geschwindigkeit auf einer vorher festgelegten Skala (zum Beispiel ).
Vektoren können addiert oder subtrahiert werden. Anschaulich ist dies in der Skizze unten dargestellt. Zunächst soll der einfachste Fall dargestellt werden. Die beiden Vektoren und zeigen in dieselbe Richtung. Um diese beiden Vektoren zu addieren, wird der Fußpunkt des einen Vektors an die Spitze des anderen Vektors gesetzt. Das Ergebnis ist ein Vektor, der in die gleiche Richtung zeigt und so lang ist wie beide Vektoren hintereinander.
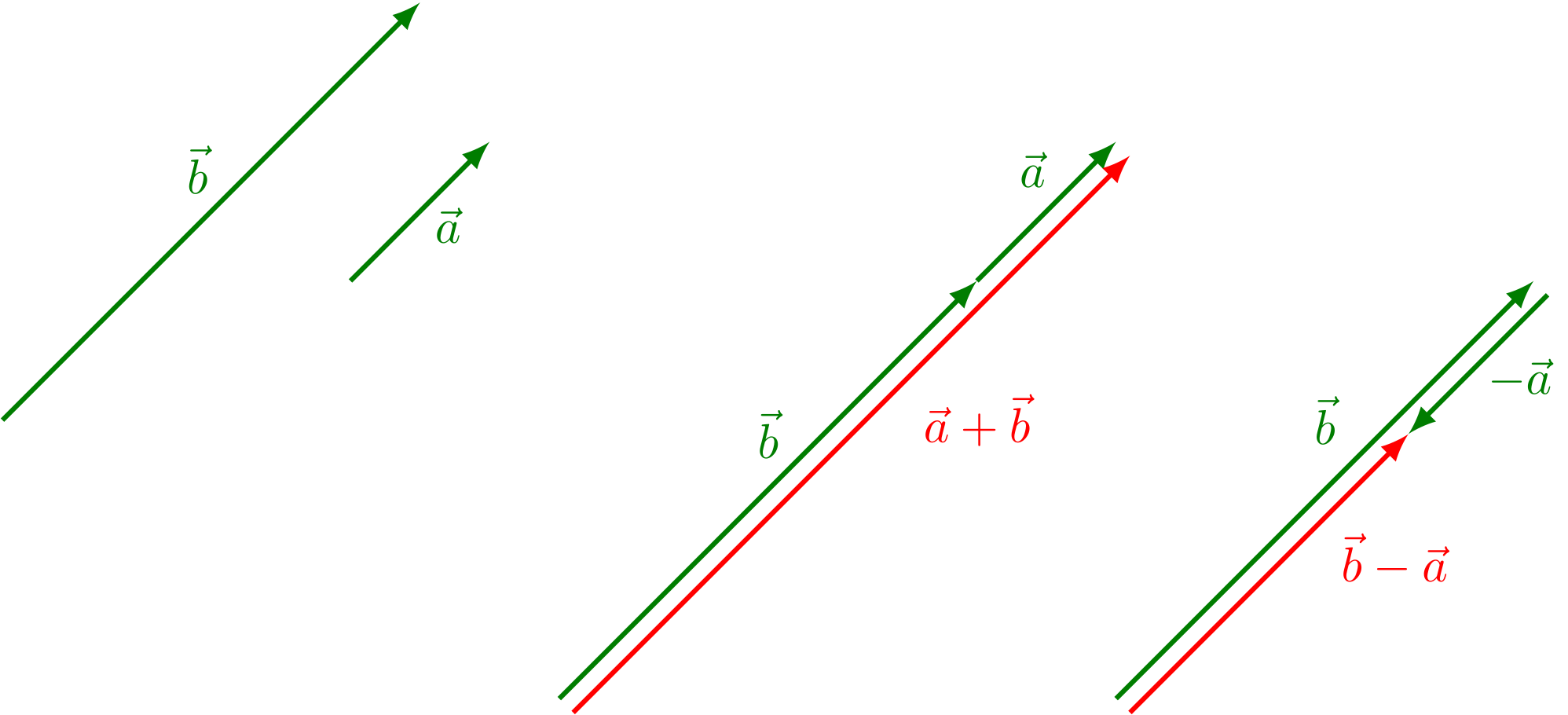
Abbildung 3.1.1: Addition und Subtraktion von Vektoren (eindimensional) (C)
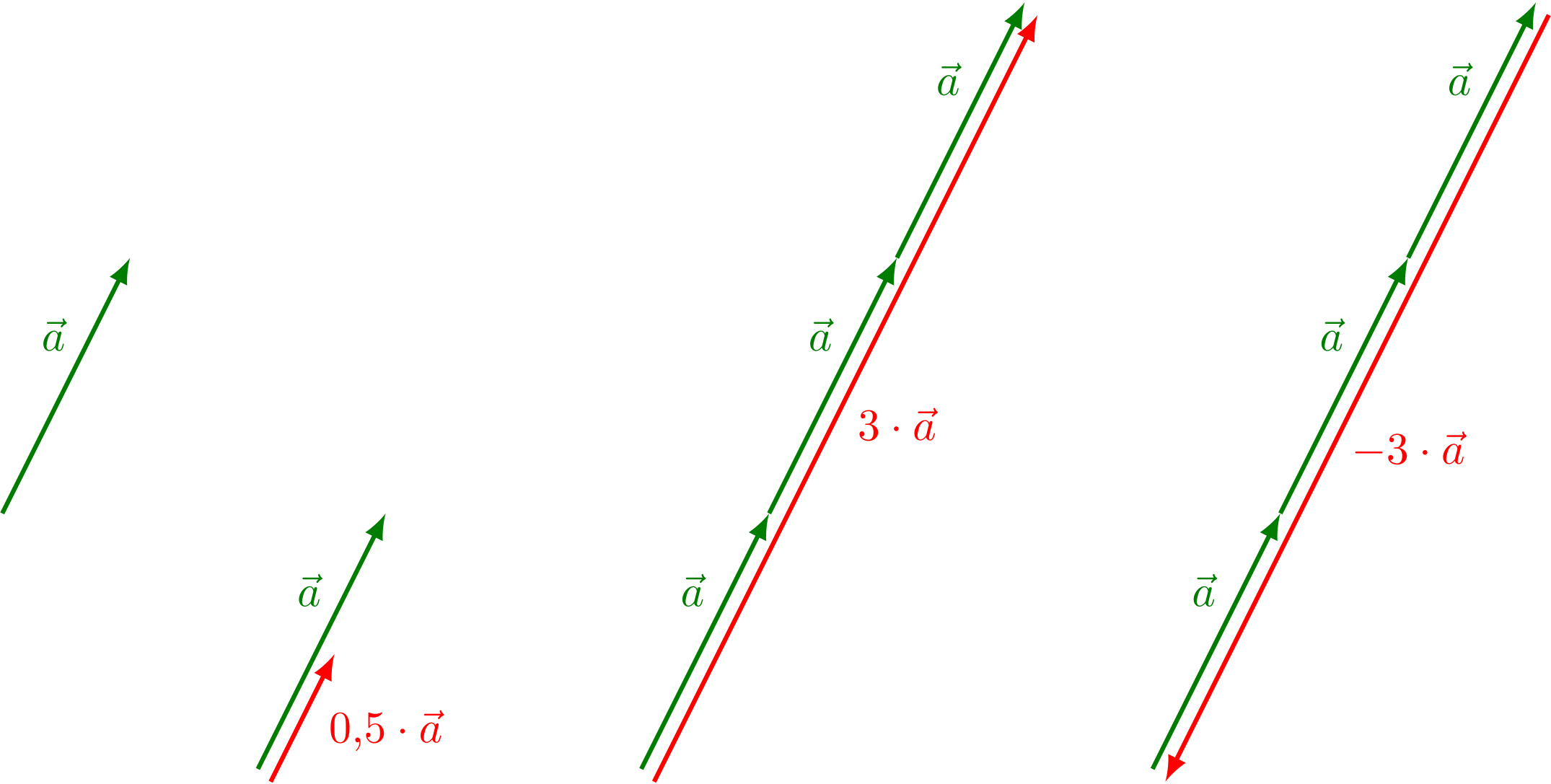
Abbildung 3.1.2: Vielfache von Vektoren: Multiplikation von Vektoren mit Skalaren (C)
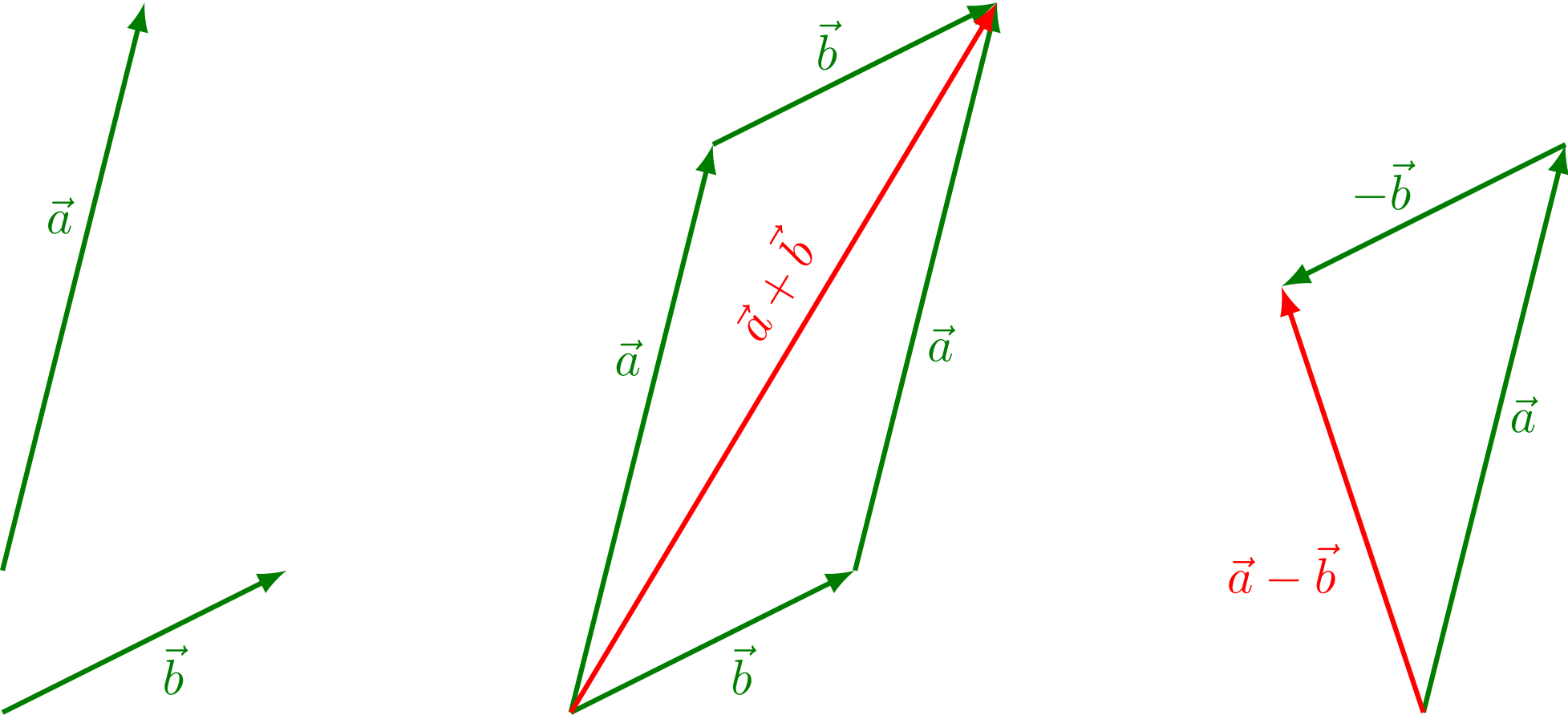
Abbildung 3.1.3: Addition und Subtraktion von Vektoren (C)
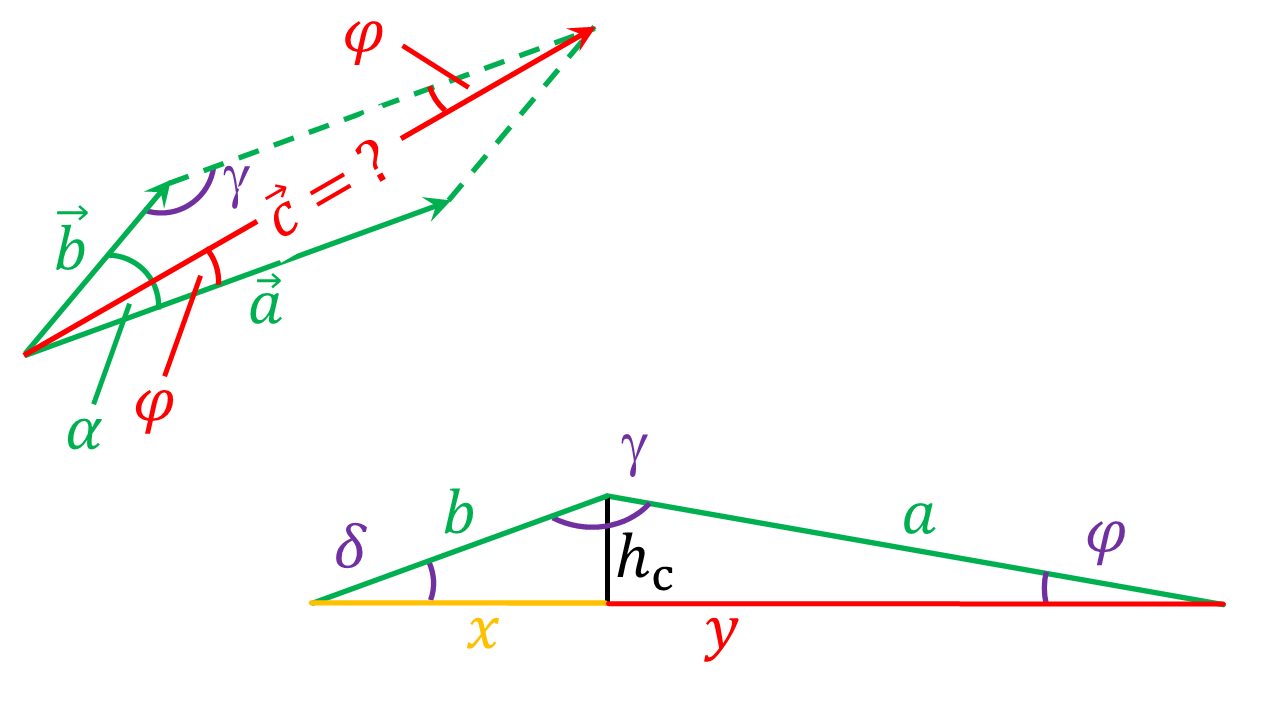
Die Richtung des resultierenden Vektors kann dann in Bezug zu den anderen Vektoren angegeben werden. Der Winkel , der zwischen Vektor und dem Vektor liegt, kann mit den Winkelfunktionen bestimmt werden:
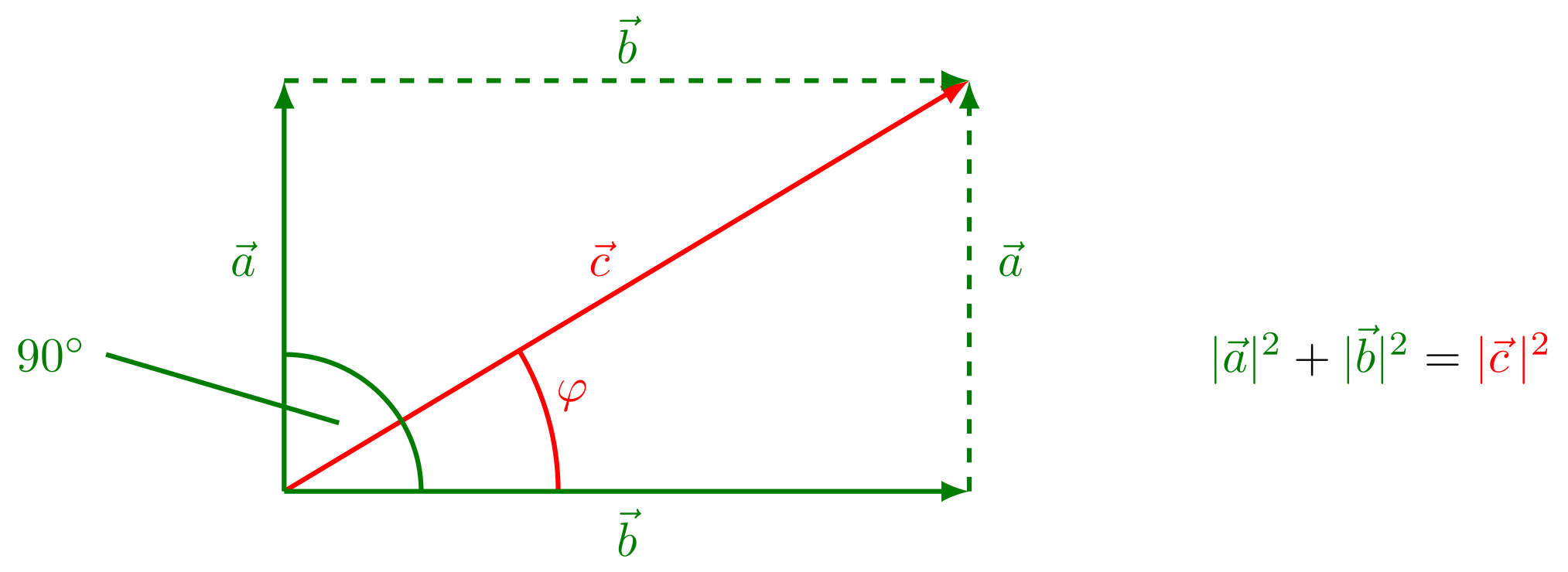
Abbildung 3.1.4: Betrag des resultierenden Vektors in rechtwinkligem Dreieck (C)
und der Kosinussatz ergibt:
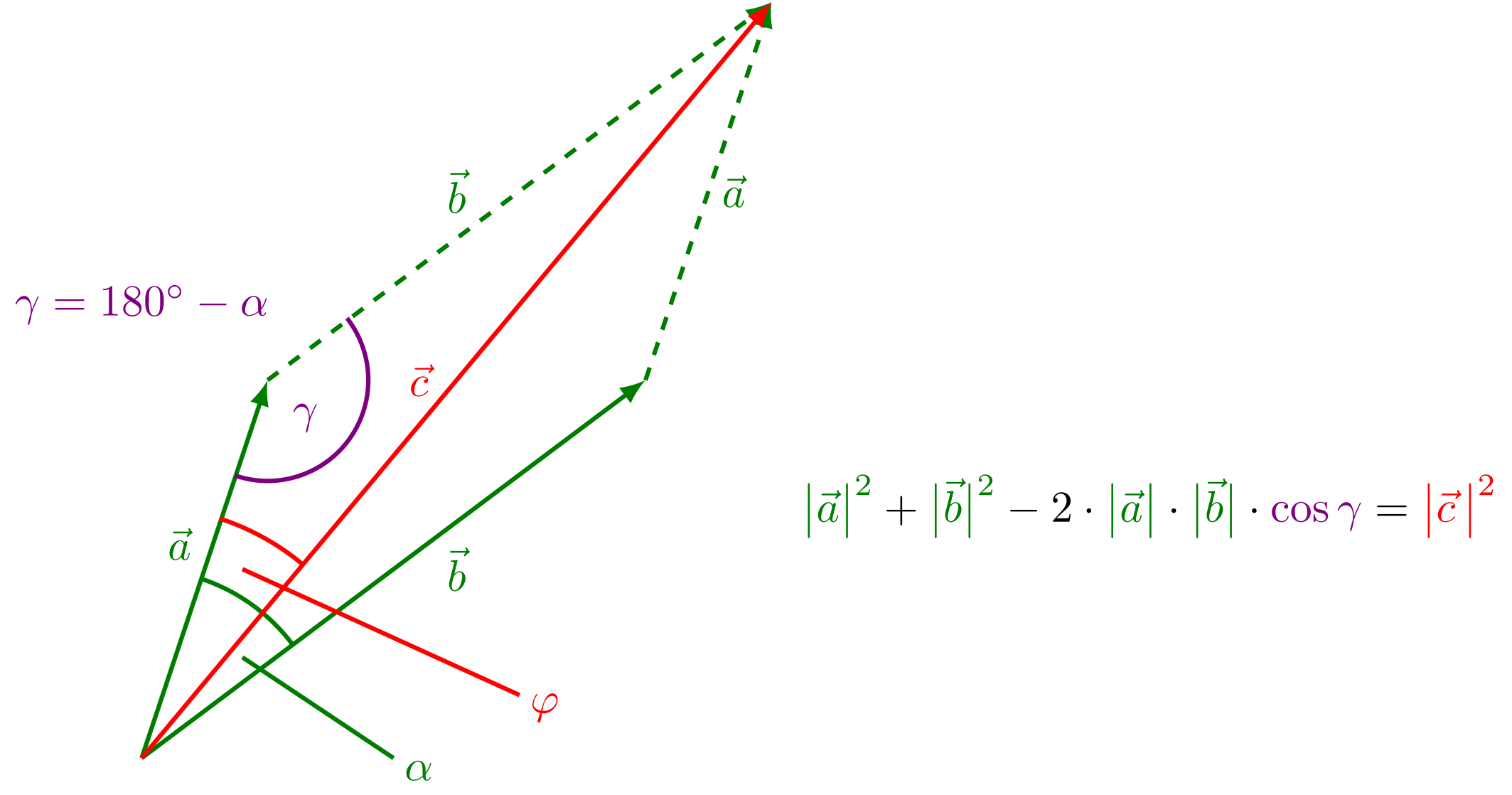
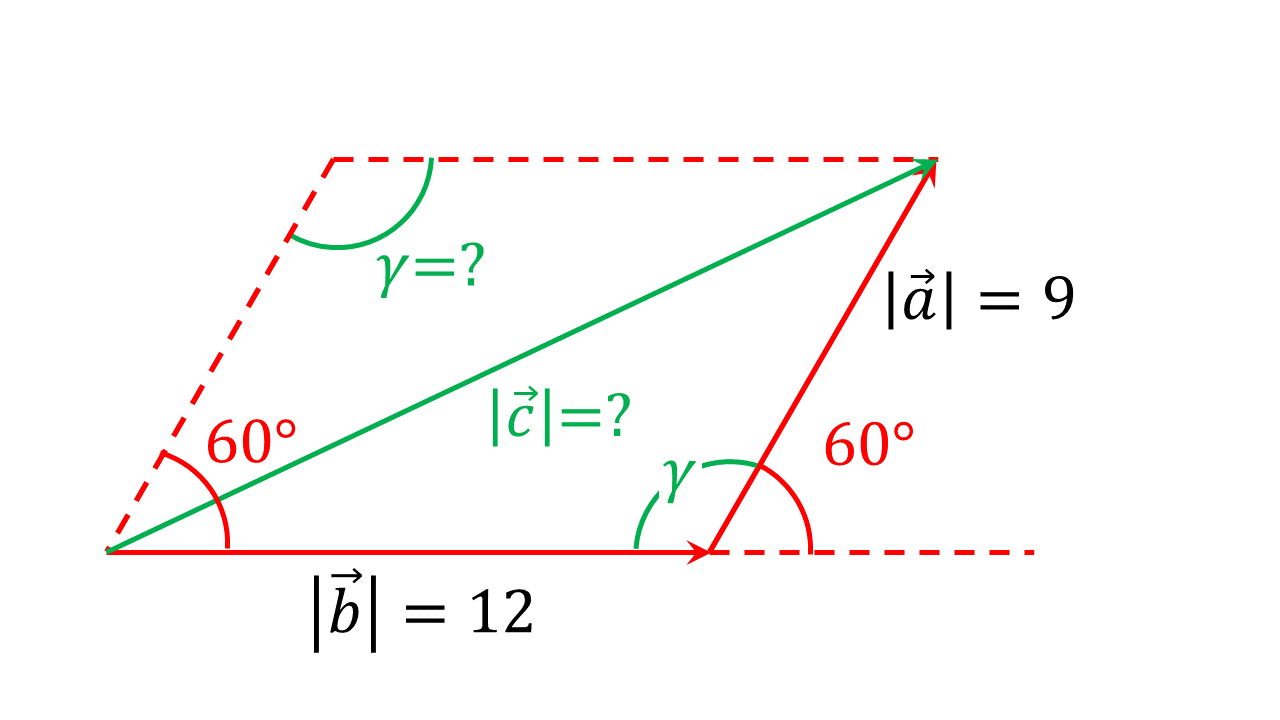
Abbildung 3.1.5: Betrag des resultierenden Vektors in beliebigem Dreieck (C)
Beispiel
3.1.21
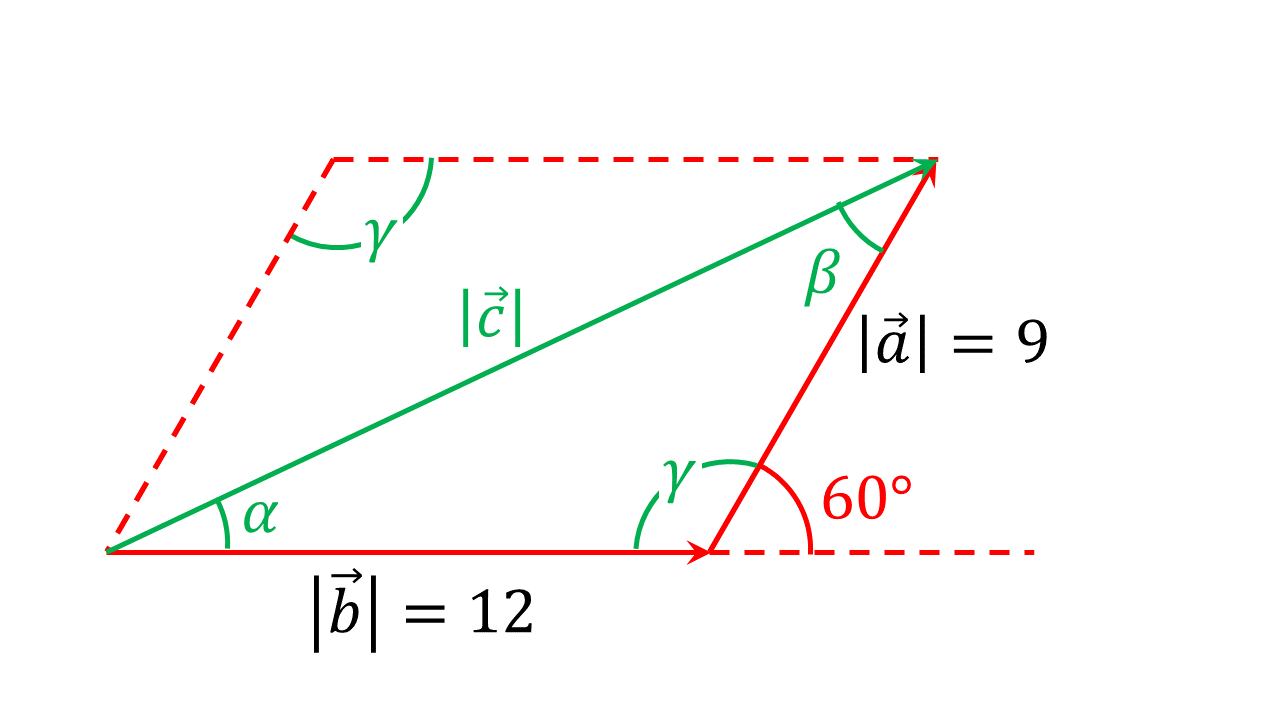
Zwei Vektoren und schließen einen Winkel von ein. Die Beträge der Vektoren liegen bei und .
Wie groß ist der Betrag des resultierenden Vektors und welchen Winkel schließt er mit Vektor ein?
Zunächst machen wir eine Skizze:
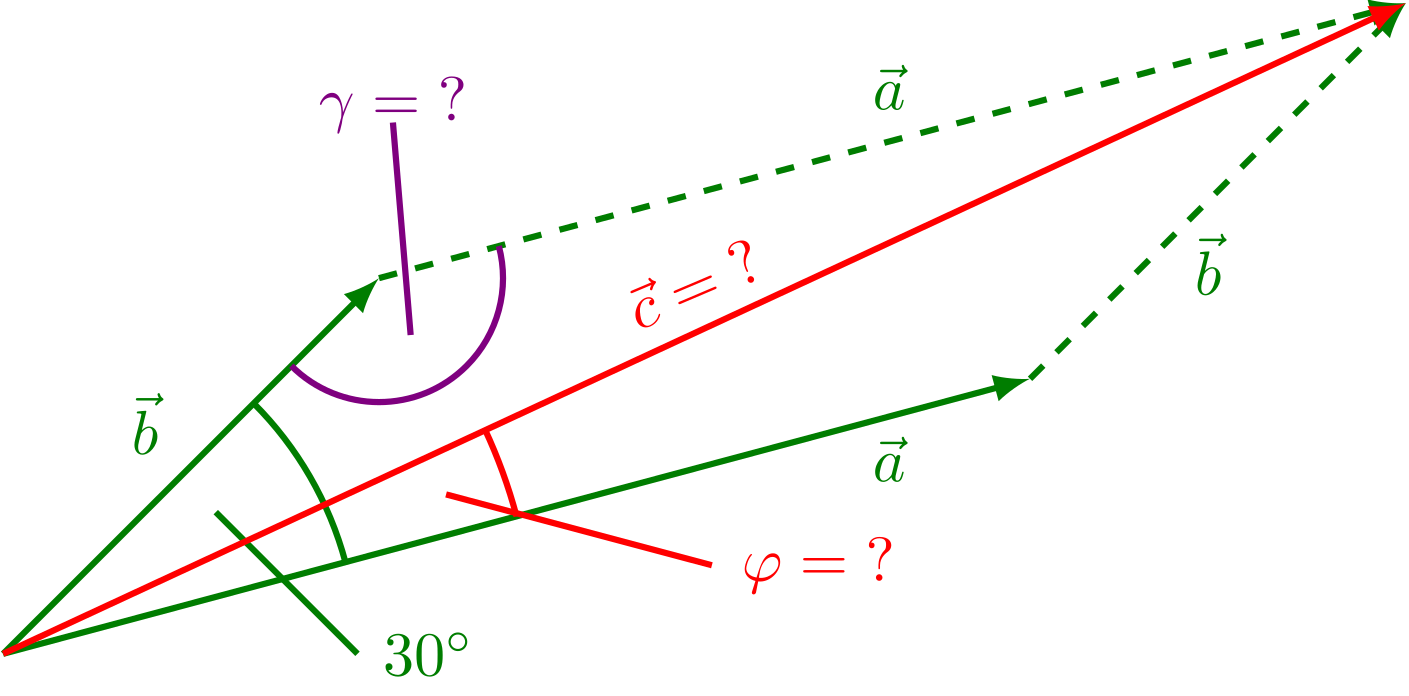
Um die gesuchten Größen (rot markiert) zu bestimmen, muss zuerst der Winkel berechnet werden. Es gilt:
Jetzt kann der Kosinussatz angewendet werden und man erhält den Betrag des resultierenden Vektors :
Mit dem Sinussatz erhalten wir für den Winkel :
Zwei Vektoren und schließen einen Winkel von ein. Die Beträge der Vektoren liegen bei und .
Wie groß ist der Betrag des resultierenden Vektors und welchen Winkel schließt er mit Vektor ein?
Zunächst machen wir eine Skizze:

Abbildung 3.1.6: Skizze der Vektoraddition zur Lösung der Aufgabe (C)
Jetzt kann der Kosinussatz angewendet werden und man erhält den Betrag des resultierenden Vektors :
Mit dem Sinussatz erhalten wir für den Winkel :
Hier finden Sie die Vektoraddition am Beispiel von Kräften:
Animation zur Vektoraddition von Walter Fendt
Basiswissen „Vektoralgebra“
Eine elegante Methode zur Behandlung von Vektoren bietet die Vektoralgebra. Dabei wird ein Vektor in Bezug zu einem Koordinatensystem beschrieben. Aufgrund der besseren Anschaulichkeit betrachten wir das Problem in der Ebene, und die Achsen des Koordinatensystems sollen rechtwinklig aufeinander stehen (ein Koordinatensystem, bei dem alle Koordinatenachsen senkrecht aufeinander stehen, bezeichnet man als kartesisches Koordinatensystem). Der Vektor liegt im Koordinatensystem mit seinem Anfangspunkt im Ursprung. Die Beschreibung des Vektors erfolgt jetzt über die Projektionen des Vektors auf die Koordinatenachsen.
In der Vektorschreibweise werden die einzelnen Koordinaten untereinander geschrieben und in eine Klammer gesetzt:
Beispiel
3.1.22
Wir betrachten den in der Abbildung gezeigten Vektor .
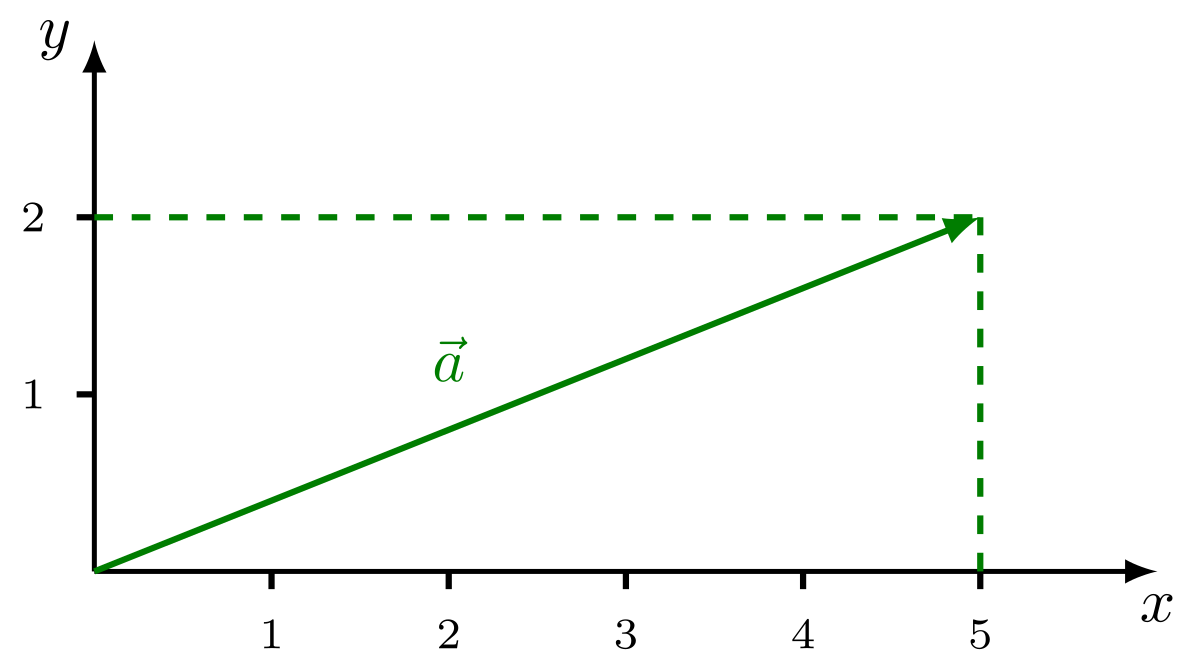
Die Projektion des Vektors auf die -Achse ergibt den Wert , und die Projektion auf die -Achse ergibt den Wert . Damit ist der Vektor durch seine Koordinaten beschrieben:
Wir betrachten den in der Abbildung gezeigten Vektor .

Abbildung 3.1.8: Darstellung eines Vektors im kartesischen Koordinatensystem (zweidimensional) (C)
Möchte man einen Vektor mit einem Skalar multiplizieren, also den Vektor strecken oder stauchen, muss jede Komponente des Vektors mit dem Skalar multipliziert werden:
Beispiel
3.1.23
Der Vektor soll mit der Zahl zwei multipliziert werden. Der Vektor soll also immer noch in die gleiche Richtung zeigen, aber doppelt so lang sein wie ursprünglich.
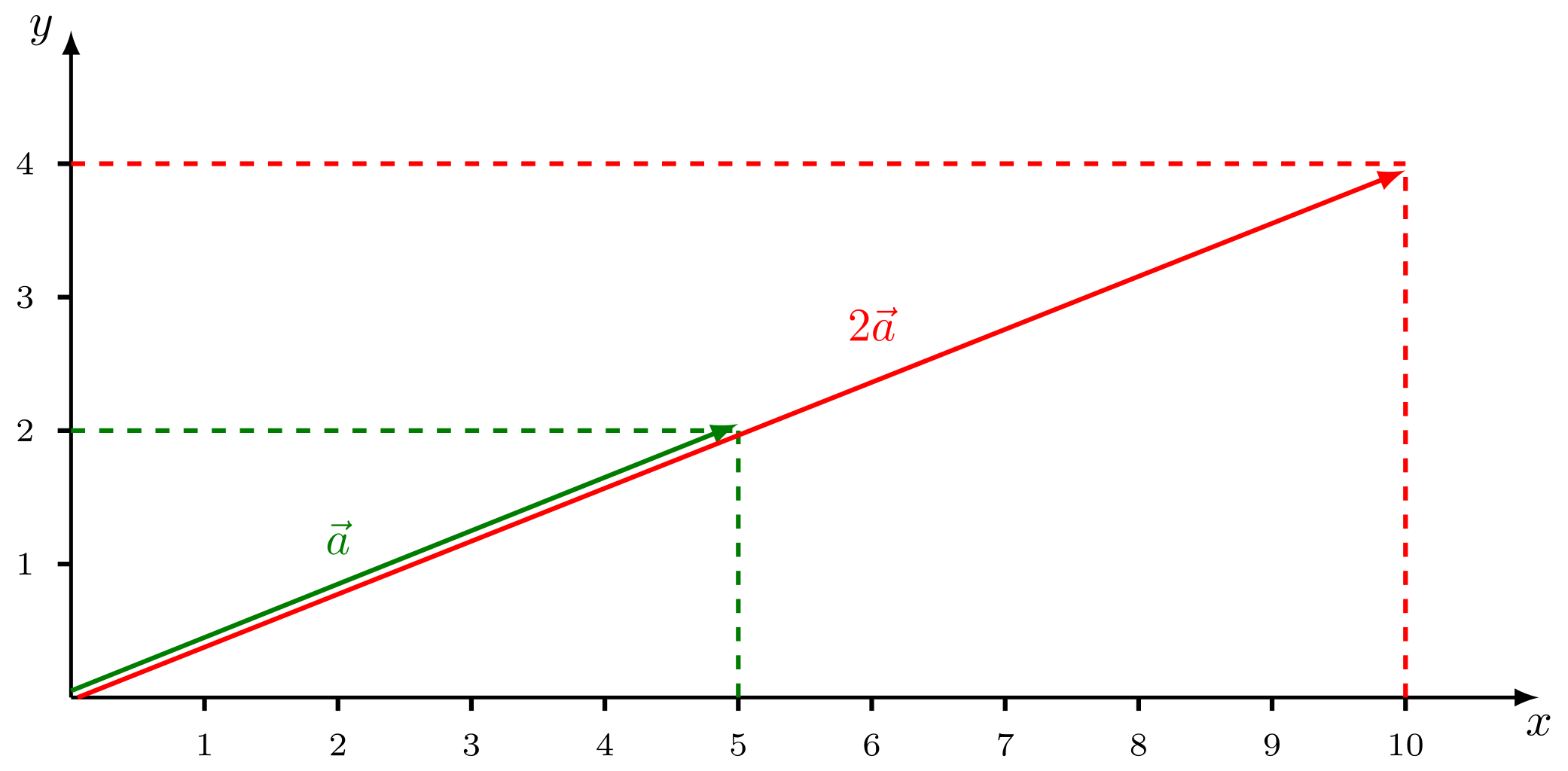
Es ergibt sich dann als Lösung:
Der Vektor soll mit der Zahl zwei multipliziert werden. Der Vektor soll also immer noch in die gleiche Richtung zeigen, aber doppelt so lang sein wie ursprünglich.

Abbildung 3.1.9: Multiplikation eines Vektors mit dem Faktor in kartesischem Koordinatensystem (zweidimensional) (C)
Die Addition oder Subtraktion von Vektoren erfolgt koordinatenweise. Jeweils die gleichen Koordinaten werden addiert oder subtrahiert. Es gelten folgende Rechenregeln:
Beispiel
3.1.24
Zwei Vektoren und sollen addiert beziehungsweise subtrahiert werden. Es ergeben sich als Summe und Differenz:
In der Abbildung ist die Aufgabe skizziert. Man setzt wie im letzten Abschnitt besprochen die Vektoren aneinander und bestimmt den resultierenden Vektor. Bei Betrachtung der Skizze wird deutlich, dass sich aufgrund der Geometrie obige Rechenregeln ergeben.
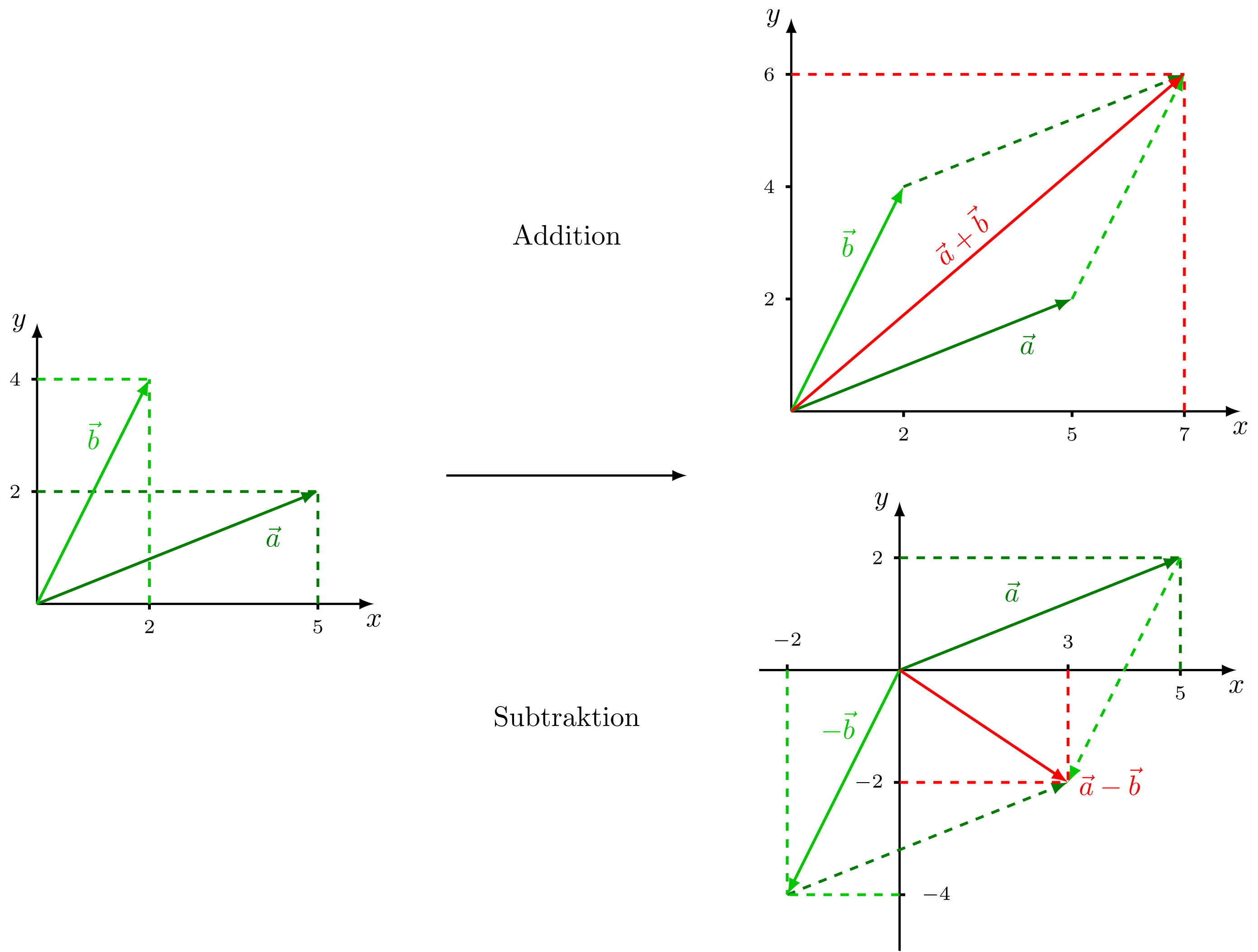
Zwei Vektoren und sollen addiert beziehungsweise subtrahiert werden. Es ergeben sich als Summe und Differenz:
In der Abbildung ist die Aufgabe skizziert. Man setzt wie im letzten Abschnitt besprochen die Vektoren aneinander und bestimmt den resultierenden Vektor. Bei Betrachtung der Skizze wird deutlich, dass sich aufgrund der Geometrie obige Rechenregeln ergeben.

Abbildung 3.1.10: Addition und Subtraktion zweier Vektoren in kartesischem Koordinatensystem (zweidimensional) (C)
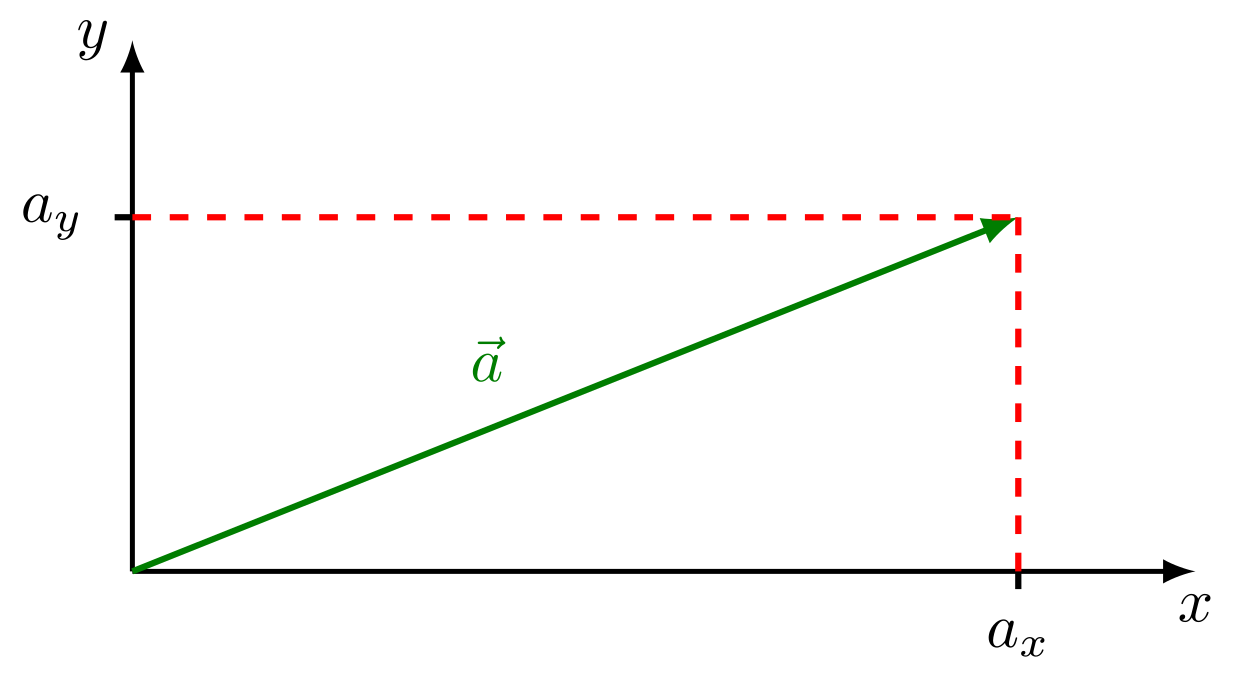
Abbildung 3.1.11: Darstellung eines Vektors in kartesischem Koordinatensystem (zweidimensional) (C)
Damit ergibt sich für den Betrag des Vektors nach dem Satz des Pythagoras:
Beispiel
3.1.25
Der Betrag des Vektors soll berechnet werden. Man erhält:
Der Betrag des Vektors soll berechnet werden. Man erhält:
In vielen Problemstellungen ist die Richtung eines Vektors gesucht, das bedeutet, man muss den Winkel , der zwischen zwei Vektoren und liegt, bestimmen. Dieser lässt sich mit Hilfe des Skalarproduktes berechnen. Dabei werden zwei Vektoren skalar miteinander multipliziert und als Ergebnis erhält man einen Skalar.
Für das Skalarprodukt gilt mit :
oder in Koordinatenschreibweise (zwei Komponenten):
oder (drei Komponenten):
oder in Koordinatenschreibweise (zwei Komponenten):
oder (drei Komponenten):
Beispiel
3.1.26
Gesucht ist der Winkel , der von den zwei Vektoren und eingeschlossen ist. Mit den obigen Beziehungen kann das Skalarprodukt über die Beträge bestimmt werden. In dieser Gleichung ist der gesuchte Winkel versteckt:
Gleichzeitig gilt für das Skalarprodukt:
Durch Gleichsetzen und Umformen erhält man den gesuchten Winkel :
Gesucht ist der Winkel , der von den zwei Vektoren und eingeschlossen ist. Mit den obigen Beziehungen kann das Skalarprodukt über die Beträge bestimmt werden. In dieser Gleichung ist der gesuchte Winkel versteckt:
Gleichzeitig gilt für das Skalarprodukt:
Durch Gleichsetzen und Umformen erhält man den gesuchten Winkel :
Zerlegung einer Kraft von Walter Fendt
Aufgabe 3.1.27
Gegeben sind die beiden in der Skizze dargestellten Vektoren und . Addieren Sie die Vektoren und berechnen Sie den Betrag des resultierenden Vektors.


Gegeben sind die beiden in der Skizze dargestellten Vektoren und . Addieren Sie die Vektoren und berechnen Sie den Betrag des resultierenden Vektors.

Abbildung 3.1.12: Vektoren und (C)
Aufgabe 3.1.28
Wenn Sie die beiden Vektoren und addieren, ergibt sich ein Vektor . Wie groß ist der Winkel , der von und eingeschlossen wird?
Geben Sie Ihr Ergebnis in auf eine Nachkommastelle gerundet an.


Wenn Sie die beiden Vektoren und addieren, ergibt sich ein Vektor . Wie groß ist der Winkel , der von und eingeschlossen wird?
Geben Sie Ihr Ergebnis in auf eine Nachkommastelle gerundet an.

Abbildung 3.1.14: Vektoren und (C)
Aufgabe 3.1.29
Gegeben sind die in der Skizze gezeigten Vektoren mit und . Der Winkel zwischen den beiden Vektoren beträgt . Berechnen Sie den Betrag des resultierenden Vektors .
Geben Sie den Wert auf eine Nachkommastelle gerundet an.
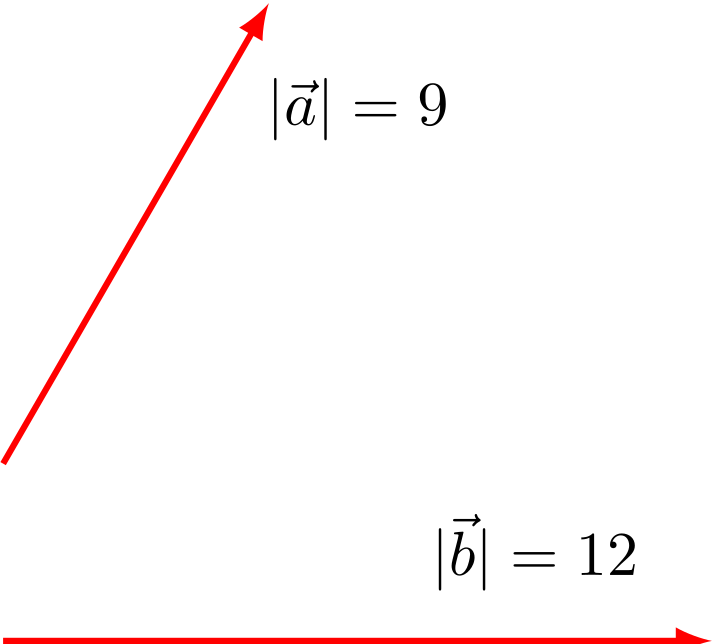

Gegeben sind die in der Skizze gezeigten Vektoren mit und . Der Winkel zwischen den beiden Vektoren beträgt . Berechnen Sie den Betrag des resultierenden Vektors .
Geben Sie den Wert auf eine Nachkommastelle gerundet an.

Abbildung 3.1.16: Vektoren und (C)
Aufgabe 3.1.30
Gegeben sind zwei Vektoren mit und . Der Winkel zwischen den beiden Vektoren beträgt . Welchen Winkel schließt der resultierende Vektor mit Vektor ein?
Tipp: Die Aufgabe ist die Fortsetzung der vorhergehenden Aufgabe.


Gegeben sind zwei Vektoren mit und . Der Winkel zwischen den beiden Vektoren beträgt . Welchen Winkel schließt der resultierende Vektor mit Vektor ein?
Tipp: Die Aufgabe ist die Fortsetzung der vorhergehenden Aufgabe.

Abbildung 3.1.18: Vektoren und (C)
Aufgabe 3.1.31
Berechnen Sie die Koordinaten , und des Vektors mit und :



Berechnen Sie die Koordinaten , und des Vektors mit und :
Aufgabe 3.1.32
Berechnen Sie den Betrag des Vektors :

Berechnen Sie den Betrag des Vektors :
Aufgabe 3.1.33
Wie groß ist der Winkel , der von den Vektoren und eingeschlossen wird?
Es gilt für und . Geben Sie das Ergebnis mit einer Nachkommastelle an.

Wie groß ist der Winkel , der von den Vektoren und eingeschlossen wird?
Es gilt für und . Geben Sie das Ergebnis mit einer Nachkommastelle an.
Aufgabe 3.1.34
Wie groß ist der Betrag des resultierenden Vektors ?
Für und gilt: und

Wie groß ist der Betrag des resultierenden Vektors ?
Für und gilt: und
Aufgabe 3.1.35
Welchen Winkel schließt der Vektor mit der -Achse ein? Geben Sie den Winkel in Grad mit einer Nachkommastelle an.

Welchen Winkel schließt der Vektor mit der -Achse ein? Geben Sie den Winkel in Grad mit einer Nachkommastelle an.
Skalare (!)
Die bisher vorgestellten physikalischen Größen sind Skalare. Sie dienen dazu, das Ausmaß einer physikalischen Größe anzugeben. Skalare können also nur angeben, ob etwas groß oder klein ist. Manche Skalare können negativ oder positiv sein. Um Skalare zu beschreiben, benötigt man nur einen Zahlenwert und eine Einheit.
Die bisher vorgestellten physikalischen Größen sind Skalare. Sie dienen dazu, das Ausmaß einer physikalischen Größe anzugeben. Skalare können also nur angeben, ob etwas groß oder klein ist. Manche Skalare können negativ oder positiv sein. Um Skalare zu beschreiben, benötigt man nur einen Zahlenwert und eine Einheit.
Beispiel
3.1.36
- Länge einer Brücke:
- Masse eines Autos:
- Dichte von Wasser:
Video 14: Definition von Vektorgrößen (C)
.
Vektoren (!)
Physikalische Größen, die zusätzlich zu einem Zahlenwert eine Richtung angeben, sind Vektoren. Für diese Größen gibt es spezielle Rechenregeln (siehe unten). Um Vektoren und Skalare in ihrer Schreibweise voneinander zu unterscheiden, werden vektorielle Größen fett gedruckt oder mit einem Pfeil über dem Zeichen dargestellt (). Betrachtet man nur den Betrag eines Vektors, reduziert man die Information des Vektors auf einen Skalar. Der Vektorbetrag wird deshalb entweder durch das Variablenzeichen in nicht fettgedruckter Schreibweise oder durch ergänzende Betragsstriche notiert (). Vektoren werden als Pfeile dargestellt. Dabei gibt die Orientierung der Pfeilspitze die Richtung der vektoriellen Größe an, während die Länge des Pfeiles den Betrag des Vektors beschreibt.
Beispiel
3.1.37
- Geschwindigkeit eines Autos (Geschwindigkeitsbetrag und Fahrtrichtung)
- Kraft einer Feder (Stärke der Federkraft und Richtung der Kraft)
Beispiel
3.1.38
Vektordarstellung: Ortsvektor und Geschwindigkeitsvektor eines Körpers.
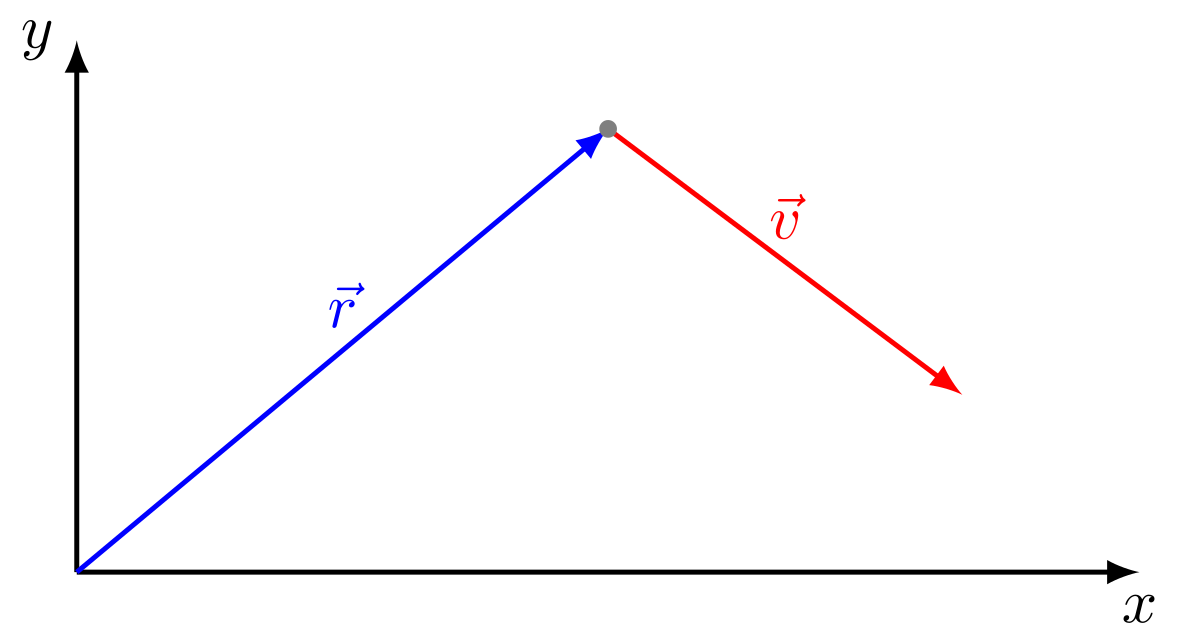
Vektordarstellung: Ortsvektor und Geschwindigkeitsvektor eines Körpers.

Abbildung 3.1.22: Darstellung der Bewegung eines Körpers mit Vektoren (C)
Kartesische Koordinaten (!)
Video 15: Kartesische Koordinaten (C)
.
Video 16: Koordinatenschreibweisen (C)
.
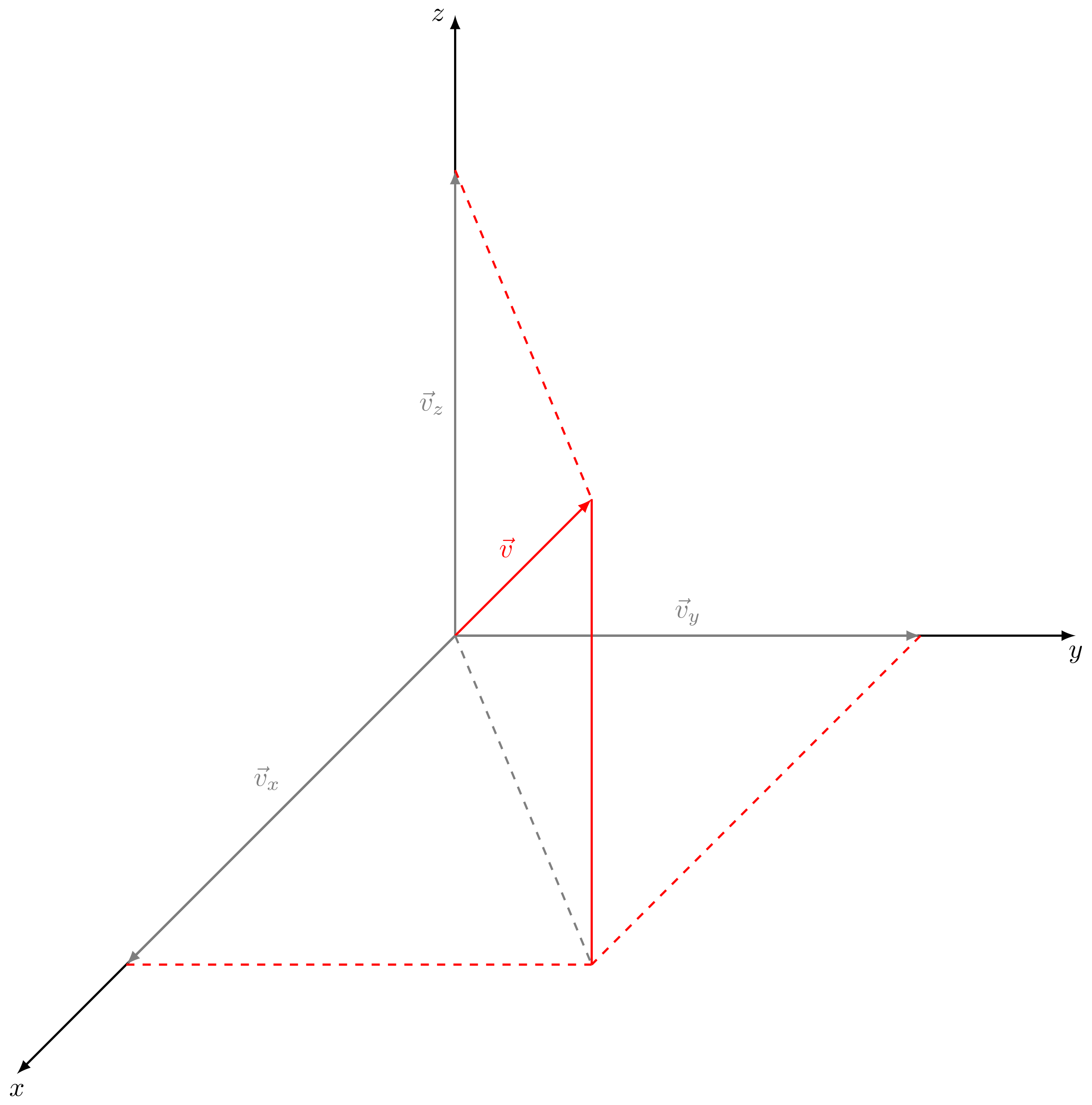
Abbildung 3.1.23: Kartesische Koordinaten (C)
Im dreidimensionalen Raum benötigt man für die Darstellung eines Vektors genau drei reelle Zahlen. Meistens werden dafür die drei Komponenten des Vektors in Richtung der -, - und -Achse eines kartesischen Koordinatensystems gewählt. Die Komponenten des Vektors bezeichnet man mit , und . Eine häufig benutzte Schreibweise für Vektoren ist der sogenannte Spaltenvektor, bei dem die einzelnen Komponenten vertikal untereinander notiert sind,
Beispiel
3.1.39
Der Geschwindigkeitsvektor eines Flugzeugs im Landeanflug betrage:
Der Geschwindigkeitsvektor eines Flugzeugs im Landeanflug betrage:
Betrag eines Vektors (!)
Video 17: Betrag eines Vektors (C)
.
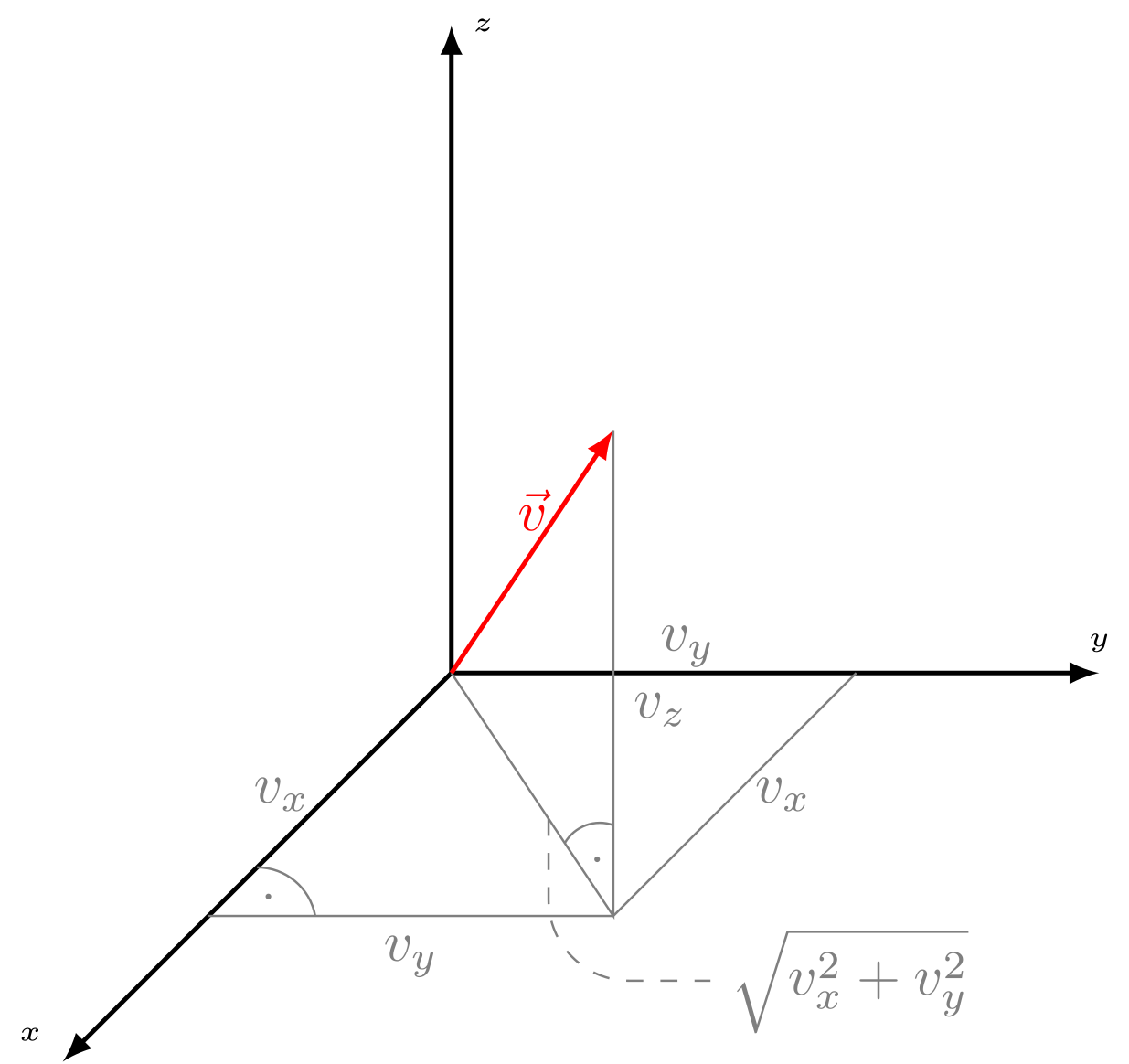
Abbildung 3.1.24: Betrag eines Vektors in kartesischem Koordinatensystem (C)
Der Betrag des Vektors ergibt sich nach dem Satz von Pythagoras zu:
Der Betrag einer Vektorgröße ist also ein Skalar.
Video 18: Beispiel für Betragsbestimmung (C)
.
Beispiel
3.1.40
Der Betrag der Geschwindigkeit des Flugzeugs aus obigem Beispiel ist:
Der Betrag der Geschwindigkeit des Flugzeugs aus obigem Beispiel ist:
Addition zweier Vektoren (!)
Video 19: Vektoraddition graphisch und in Koordinatenschreibweise (C)
.
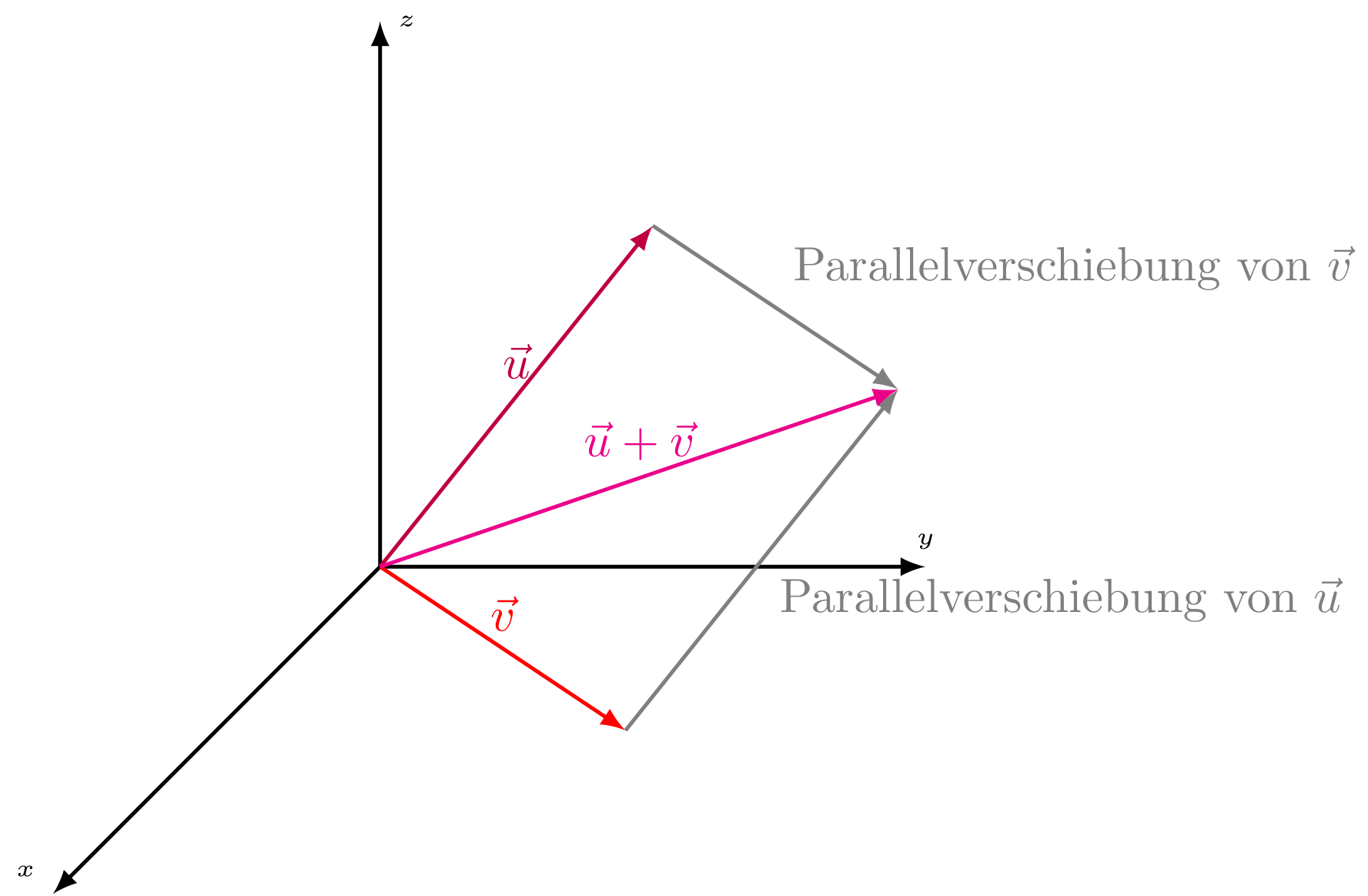
Abbildung 3.1.25: Addition von Vektoren (C)
Die Addition von zwei Vektoren erfolgt einfach durch die Addition der einzelnen kartesischen Komponenten:
Die Summe zweier Vektoren ist wieder ein Vektor.
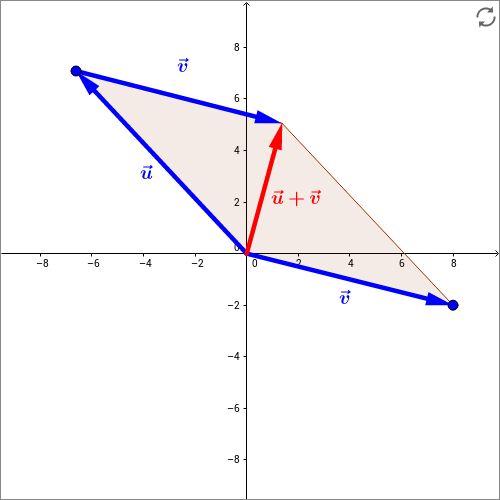
Skizze: In der folgenden interaktiven Skizze ist die Addition zweier Vektoren und graphisch in einer Ebene dargestellt. Die beiden Vektoren liegen hier in der --Ebene. Aus der Mathematik ist man vermutlich gewohnt, dass die beiden zu summierenden Vektoren aneinandergehängt werden. Der Vektor zwischen dem Ursprung des ersten Vektors und der Pfeilspitze des zweiten Vektors ist dann der Summenvektor. In der Physik werden die Vektoren meistens vom gleichen Punkt aus abgetragen (roter Vektor in der Skizze). Der Summenvektor ergibt sich dann als die Diagonale des entstehenden Vektor-Parallelogramms. Der Grund für diese Darstellung ist, dass Vektoren sich oft auf einen Massenpunkt oder einen Ortspunkt beziehen. Ein Beispiel wäre die Berechnung der Gesamtkraft aus zwei Kräften, die an einem Körper angreifen. Hier wäre es nicht intuitiv, wenn der Ursprung einer der beiden Kraftvektoren an die Pfeilspitze des anderen Kraftvektors verschoben würde, da ja beide Kräfte am Körper angreifen. In der vorliegenden Skizze wurden beide Möglichkeiten in eine Darstellung integriert, indem der Vektor einmal am Bezugspunkt und einmal an der Pfeilspitze des Vektors abgetragen wurde. Wie man sieht, ergibt sich für den Summenvektor natürlich das gleiche Ergebnis. Das Vektor-Parallelogramm ist als schattierte Fläche dargestellt. Ziehen Sie an den Pfeilspitzen und ändern Sie so auch den Summenvektor. Probieren Sie, den Summenvektor zum Verschwinden zu bringen. Wann wird bei einer gegebenen Länge der Ausgangsvektoren der Summenvektor maximal?
Skalarprodukt zweier Vektoren (!)
Video 20: Skalarprodukt (C)
.
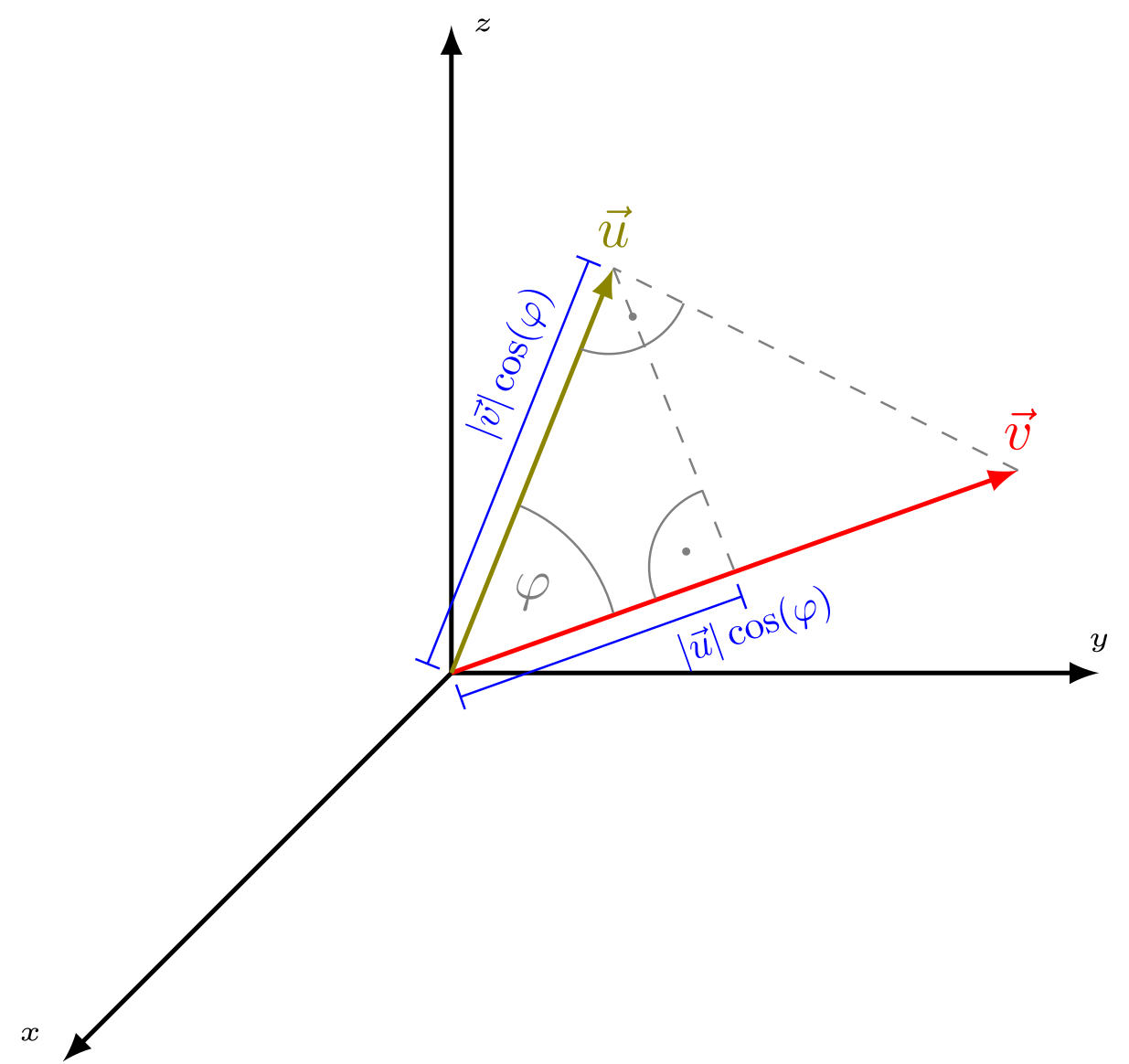
Abbildung 3.1.27: Skalarprodukt (C)
Bei Vektoren gibt es zwei Arten der Produktbildung, die sich mathematisch und in ihrer Bedeutung unterscheiden. Die erste Möglichkeit ist das Skalarprodukt (auch Punkt-Produkt genannt). Hier wird ein Punkt () als Rechenzeichen zwischen die beiden Vektoren gesetzt. Das Ergebnis des Skalarprodukts ist ein Skalar. In der kartesischen Darstellung der Vektoren wird das Skalarprodukt berechnet, indem man die sich entsprechenden Komponenten der beiden Vektoren miteinander multipliziert und danach die Summe über die gewonnenen Produkte bildet. Alternativ kann es aus dem Produkt der beiden Vektorbeträge und des Kosinus des Zwischenwinkels der beiden Vektoren berechnet werden:
wobei . Die Länge erhält man, indem man den Vektor auf die Richtung des Vektors projiziert. Das Vorzeichen von wählt man dann so wie das Vorzeichen von , also positiv, wenn die Projektion in Richtung des Vektors erfolgt, und negativ, wenn sie entgegengesetzt gerichtet ist. Üblicherweise wird als Winkel zwischen zwei Vektoren derjenige gewählt, der zwischen und liegt, der alternative Winkel ist dann . Wegen ist das Ergebnis aber das gleiche.
Das Skalarprodukt ist kommutativ, es gilt also .
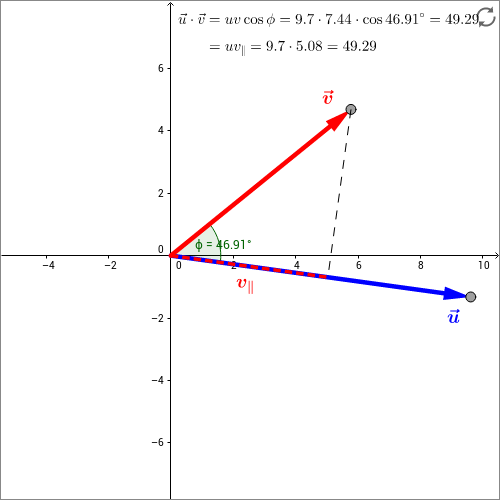
Skizze: In der folgenden interaktiven Skizze wird das Skalarprodukt der Vektoren und graphisch in einer Ebene dargestellt. Die beiden Vektoren liegen hier in der --Ebene. Ziehen Sie an den Pfeilspitzen und ändern Sie so das Skalarprodukt. Zu sehen ist die Berechnung des Skalarprodukts. Sie aktualisiert sich jeweils interaktiv bei Änderungen an den Vektoren. Oben rechts in der Skizze sieht man in der oberen Zeile die jeweils passende mathematische Berechnung mit Hilfe der Vektorbeträge und des Zwischenwinkels. In der unteren Zeile wird die Projektion des einen Vektors auf die Richtung des anderen genutzt, um das Skalarprodukt zu berechnen. Wann verschwindet das Skalarprodukt und wann wird es maximal? Wann wird das Skalarprodukt negativ?
Vektorprodukt zweier Vektoren (+)
Video 21: Vektorprodukt (C)
.
Vektorprodukt: Einführung
Eine zweite Möglichkeit der Produktbildung von Vektoren ist das Vektorprodukt. Beim Vektorprodukt (auch Kreuzprodukt genannt) wird ein Kreuz () als Rechenzeichen zwischen die beiden Vektoren gesetzt. Das Ergebnis eines Vektorprodukts ist wieder ein Vektor. In der kartesischen Darstellung kann das Vektorprodukt mit Hilfe der nachfolgend beschriebenen Rechenregel aus den Komponenten der Vektoren berechnet werden. Dabei ergibt sich die Richtung des Ergebnisvektors so, dass er senkrecht auf der Ebene steht, in der die beiden Vektoren liegen (für die Richtung gilt die „Rechte-Hand-Regel“):
Eine zweite Möglichkeit der Produktbildung von Vektoren ist das Vektorprodukt. Beim Vektorprodukt (auch Kreuzprodukt genannt) wird ein Kreuz () als Rechenzeichen zwischen die beiden Vektoren gesetzt. Das Ergebnis eines Vektorprodukts ist wieder ein Vektor. In der kartesischen Darstellung kann das Vektorprodukt mit Hilfe der nachfolgend beschriebenen Rechenregel aus den Komponenten der Vektoren berechnet werden. Dabei ergibt sich die Richtung des Ergebnisvektors so, dass er senkrecht auf der Ebene steht, in der die beiden Vektoren liegen (für die Richtung gilt die „Rechte-Hand-Regel“):
Video 22: Betrag des Vektorprodukts (C)
.
Vektorprodukt: Betrag
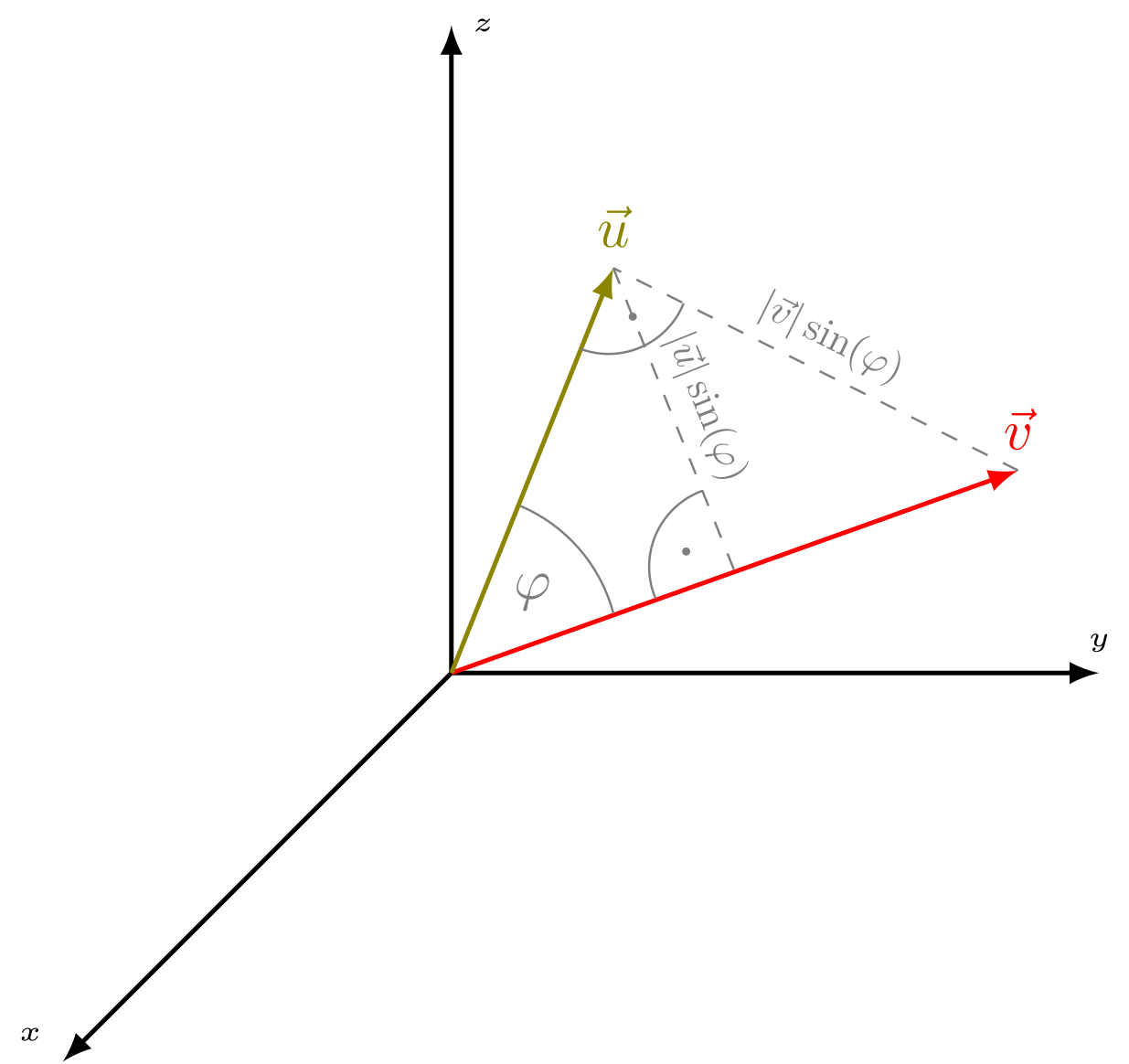
Der Betrag des Vektorprodukts ist gleich dem Produkt der Vektorbeträge und dem Betrag des Sinus des Zwischenwinkels:
wobei . Die Länge erhält man, indem man den Vektor auf die Ebene senkrecht zum Vektor projiziert – diese Projektion liegt in der durch und aufgespannten Ebene. Bei der Standardwahl für den Zwischenwinkel, , ist der Sinus stets nicht negativ, und die Betragsstriche um den Sinus können dann entfallen. Der Betrag des Vektorprodukts, , entspricht der Fläche des von und aufgespannten Parallelogramms.

Abbildung 3.1.29: Vektorprodukt (C)
Der Betrag des Vektorprodukts ist gleich dem Produkt der Vektorbeträge und dem Betrag des Sinus des Zwischenwinkels:
wobei . Die Länge erhält man, indem man den Vektor auf die Ebene senkrecht zum Vektor projiziert – diese Projektion liegt in der durch und aufgespannten Ebene. Bei der Standardwahl für den Zwischenwinkel, , ist der Sinus stets nicht negativ, und die Betragsstriche um den Sinus können dann entfallen. Der Betrag des Vektorprodukts, , entspricht der Fläche des von und aufgespannten Parallelogramms.
Vektorprodukt: Eigenschaften
Das Vektorprodukt ist nicht kommutativ, genauer gesagt ist es antikommutativ, denn es gilt .
Das Vektorprodukt ist nicht kommutativ, genauer gesagt ist es antikommutativ, denn es gilt .
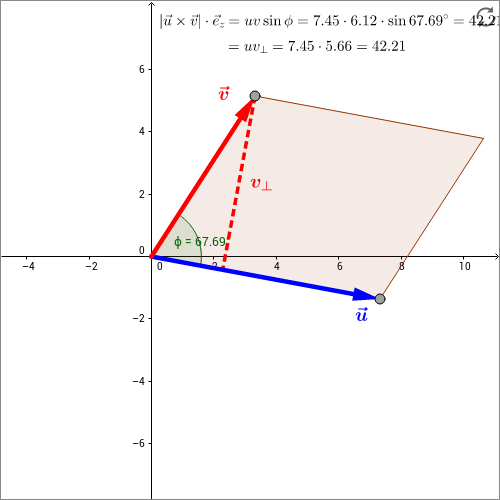
Skizze: In der folgenden interaktiven Skizze wird das Vektorprodukt der Vektoren und graphisch in einer Ebene dargestellt. Die beiden Vektoren liegen in der --Ebene. Ziehen Sie an den Pfeilspitzen und ändern Sie so das Vektorprodukt. Zu sehen ist die Berechnung des Vektorprodukts. Sie aktualisiert sich jeweils mit Ihren Änderungen an den Vektoren. Da beide Vektoren in der --Ebene liegen, wird das Ergebnis des Vektorprodukts ein Vektor entlang der -Achse sein (senkrecht zur Bildschirmebene). Daher wird nur die -Komponente des Ergebnisvektors berechnet und angegeben. Ist das angegebene Ergebnis positiv, zeigt der Ergebnisvektor aus der Bildschirmebene heraus, ist es negativ, zeigt er in die Bildschirmebene hinein. In der ersten Zeile wird die Rechnung mit Hilfe der Vektorbeträge und des Zwischenwinkels durchgeführt. Dieser wird dabei so gewählt, dass der Vektor gegen den Uhrzeigersinn auf den Vektor zu gedreht wird. In der zweiten Zeile wird die Projektion des einen Vektors auf die Richtung senkrecht zu der des anderen genutzt, um das Vektorprodukt zu berechnen. Darüber hinaus wird das Parallelogramm gezeigt, das von den beiden Vektoren und aufgespannt wird. Seine Fläche ist durch den Betrag des Vektorprodukts, , gegeben. Wann verschwindet das Vektorprodukt und wann wird es maximal? Wann wird die -Komponente des Vektorprodukts negativ?
Video 23: Richtung des Vektorprodukts (C)
.
Vektorprodukt: Richtung
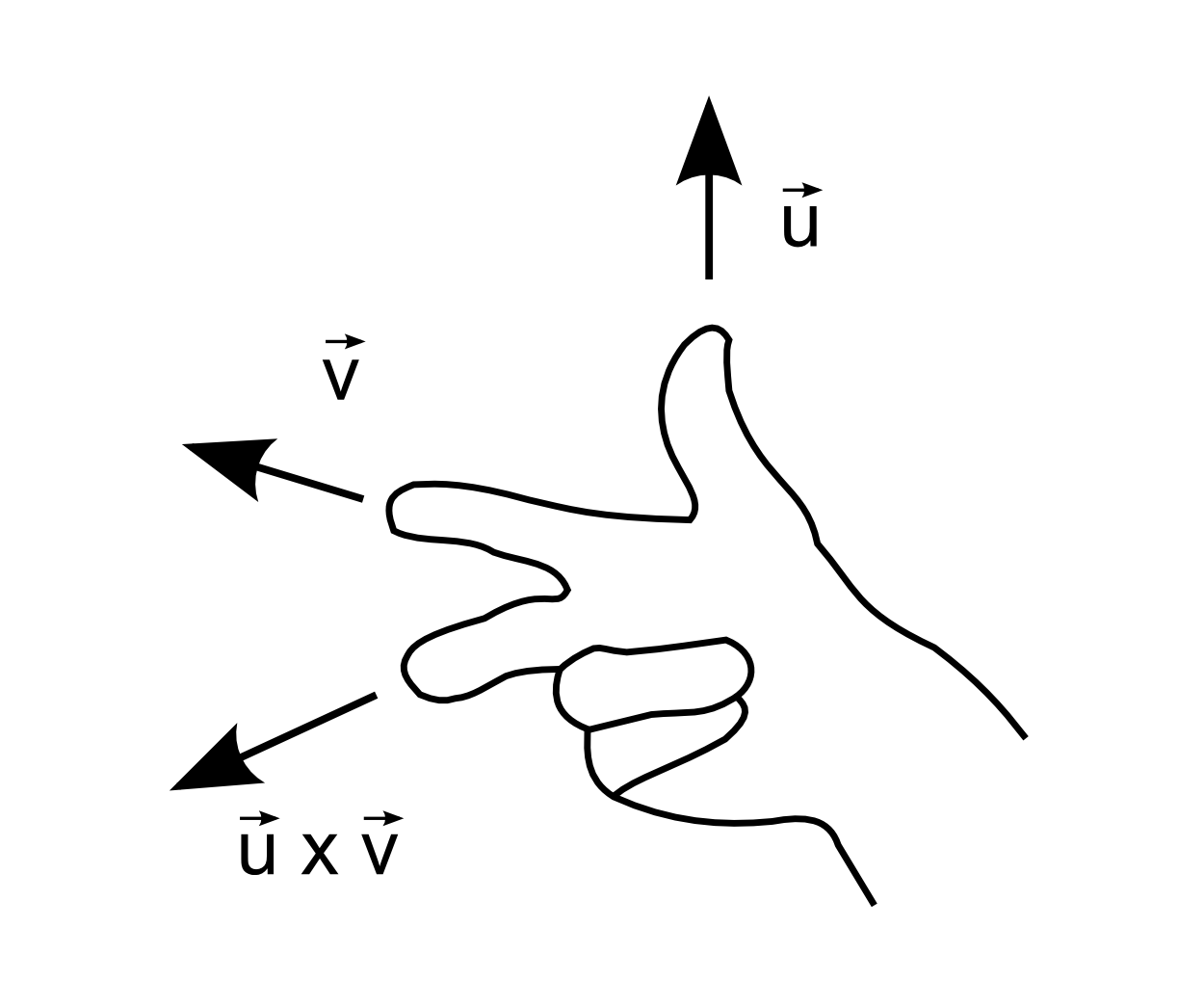
Für die Richtung des Ergebnisvektors des Vektorprodukts gilt wie oben gesagt die „Rechte-Hand-Regel“, d.h., wenn Sie mit dem Daumen der rechten Hand in Richtung und mit dem Zeigefinger in Richtung zeigen, dann gibt die Richtung des Mittelfingers die Richtung des Ergebnisvektors von an:
Für die Richtung des Ergebnisvektors des Vektorprodukts gilt wie oben gesagt die „Rechte-Hand-Regel“, d.h., wenn Sie mit dem Daumen der rechten Hand in Richtung und mit dem Zeigefinger in Richtung zeigen, dann gibt die Richtung des Mittelfingers die Richtung des Ergebnisvektors von an: