8.2.2 Brechung, Reflexion und Transmission
Video 2: Brechung, Reflexion, Transmission (C)
.
Brechung, Reflexion und Transmission (+)
Wenn eine Welle bei ihrer Ausbreitung auf ein anderes Medium (Hindernis) trifft, nimmt dessen Oberflächenstruktur die Energie der Welle auf, und von jedem Punkt der Oberfläche geht eine neue kugelförmige Elementarwelle aus (Huygens’sches Prinzip), die sich mit der gleichen Frequenz in alle Richtungen ausbreitet. Die Einhüllenden dieser Elementarwellen bilden neue Wellenfronten mit veränderter Wellenlänge, die dann im Brechungswinkel von der Grenzfläche ausgehen.
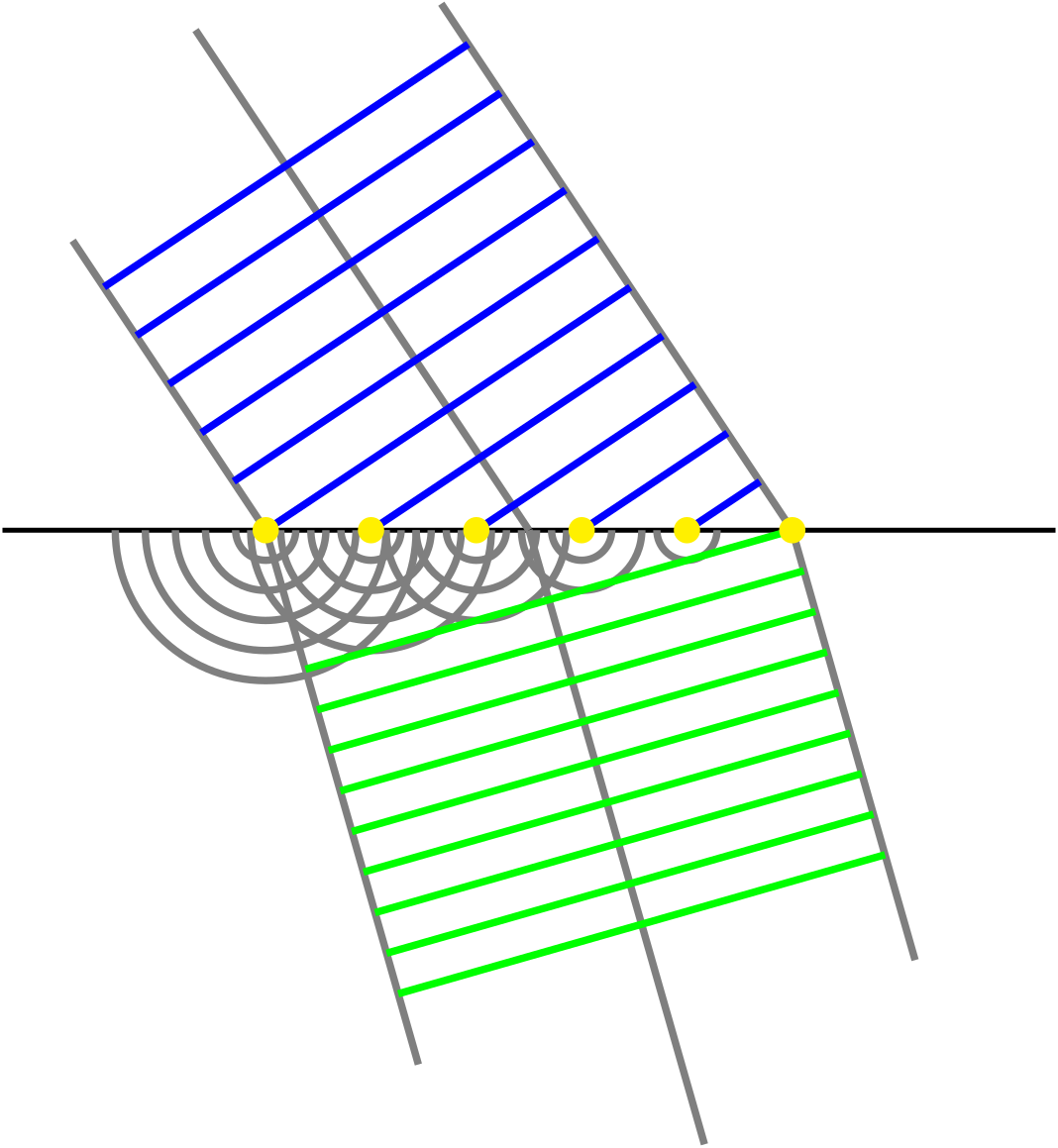
Abbildung 8.2.33: Brechung: Veranschaulichung nach dem huygensschen Prinzip (C)
| Wellentyp | Physikalischer Mechanismus |
| Mechanisch (z.B. Schall) | Die Oberflächenstruktur nimmt die ankommende Energie durch Kompression auf und sendet bei der elastischen Rückbildung eine neue mechanische Kugelwelle aus |
| Elektromagnetisch (z.B. Licht) | Die Elektronen der Oberflächenatome nehmen die Energie der ankommenden Welle kurz auf und geben sie dann in Form einer neuen elektromagnetischen Kugelwelle wieder ab. |
Brechungsgesetz von Snellius
Gilt für alle Wellen, bei elektromagnetischen Wellen wird der Brechungsindex verwendet, bei mechanischen Wellen die Wellenzahl des jeweiligen Mediums.
Gilt für alle Wellen, bei elektromagnetischen Wellen wird der Brechungsindex verwendet, bei mechanischen Wellen die Wellenzahl des jeweiligen Mediums.
| Elektromagn. Wellen (z.B. Licht) | |
| Brechungsindex | |
| Mechanische Wellen (z.B. Schall) | |
| Für alle Wellen gilt: |

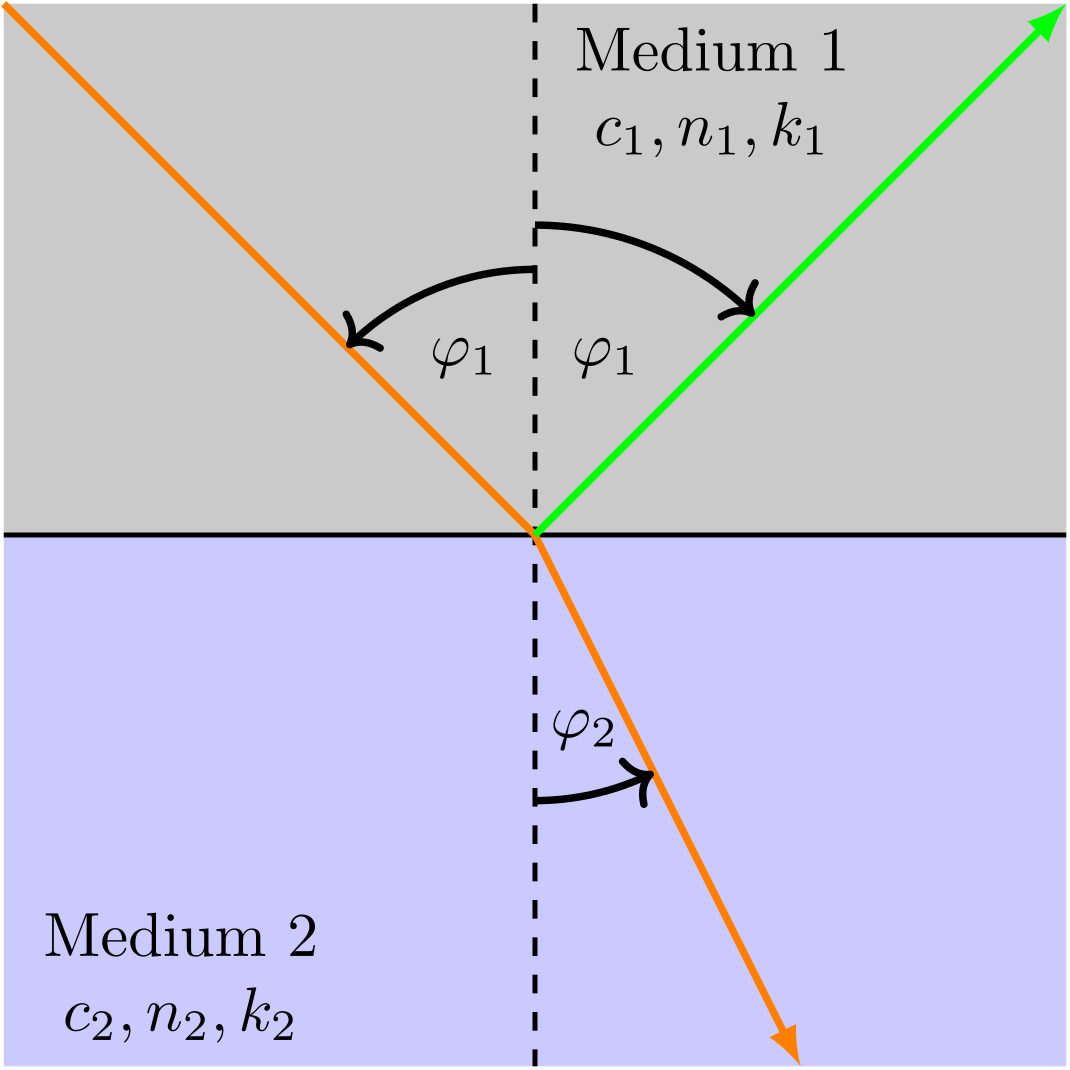
Abbildung 8.2.34: Skizze zum Brechungsgesetz von Snellius. (C)
- Dabei ist die Ausbreitungsgeschwindigkeit im Vakuum und in dem betrachteten Medium (Dielektrikum). Der Brechungsindex für elektromagnetische Wellen hängt von der relativen Permittivität (Dielektrizitätszahl) und relativen Permeabilität ab.
- Bei der Ausbreitung von mechanischen Wellen in Festkörpern unterscheidet man zwischen Druckwellen (P) und Scherwellen (S). Wenn eine einlaufende Druckwelle reflektiert bzw. gebrochen wird, entstehen sowohl Druck- als auch Scherwellen, die sich danach mit verschiedenen Winkeln ausbreiten. In Flüssigkeiten und Gasen gibt es nur Druckwellen (Longitudinalwellen).
Beim Übergang in ein optisch dichteres Medium () tritt zwischen senkrecht einfallender und reflektierter Welle ein Phasensprung von bzw. auf, anders herum dagegen nicht.
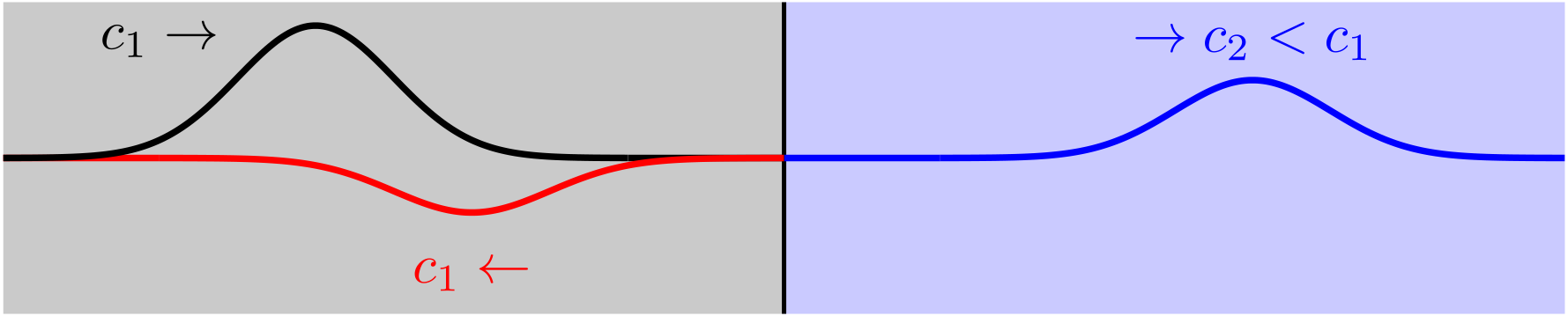
Abbildung 8.2.35: Phasensprung bei Reflektion an optisch dichterem Medium. (C)
Totalreflexion
Beim Übergang von einem (optisch) dichteren in ein weniger dichtes Medium wird der Strahl von der Lotrichtung weg gebrochen. Ist der Austrittswinkel erreicht, spricht man beim Einfallswinkel vom Grenzwinkel. Vergrößert sich der Einfallswinkel weiter, tritt Totalreflexion auf (schraffierter Bereich). Aus dem Snellius’schen Gesetz folgt:
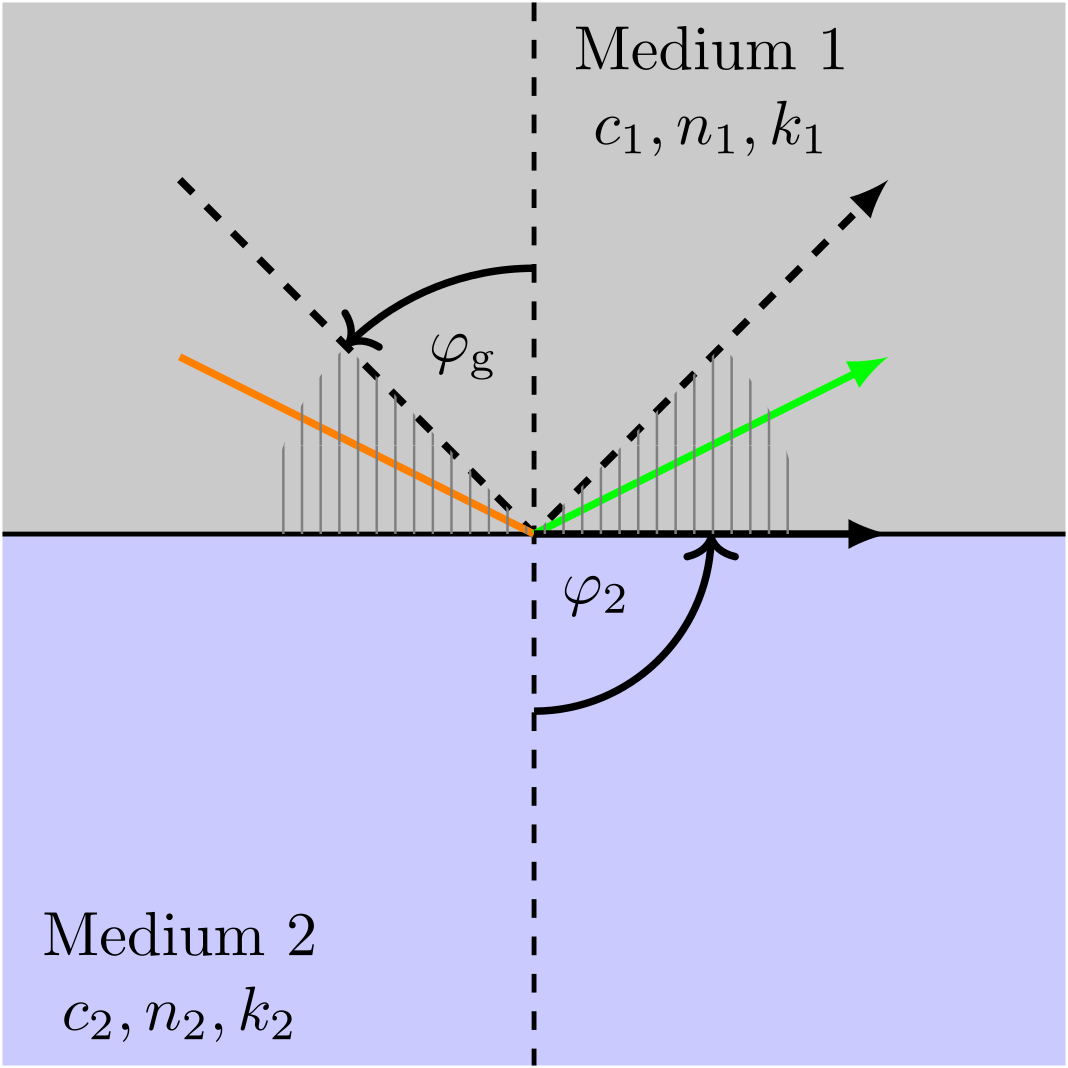
Abbildung 8.2.36: Skizze zur Totalreflexion ( bzw. ) (C)
Streuung
Wenn die Reflexion von Wellen auf Grund der Oberflächenbeschaffenheit eines Mediums ungebündelt und statistisch in alle Richtungen erfolgt, spricht man von Streuung.
Energiebetrachtungen
Je nach Einfallwinkel und Material der angrenzenden Medien teilen sich die Energie und Intensität der ankommenden Welle in verschiedene Anteile auf:
Die absorbierte Energie wird z.B. durch Dissipation in Wärme umgewandelt oder (bei Schallwellen) im Hindernis als Körperschall weitergeleitet.
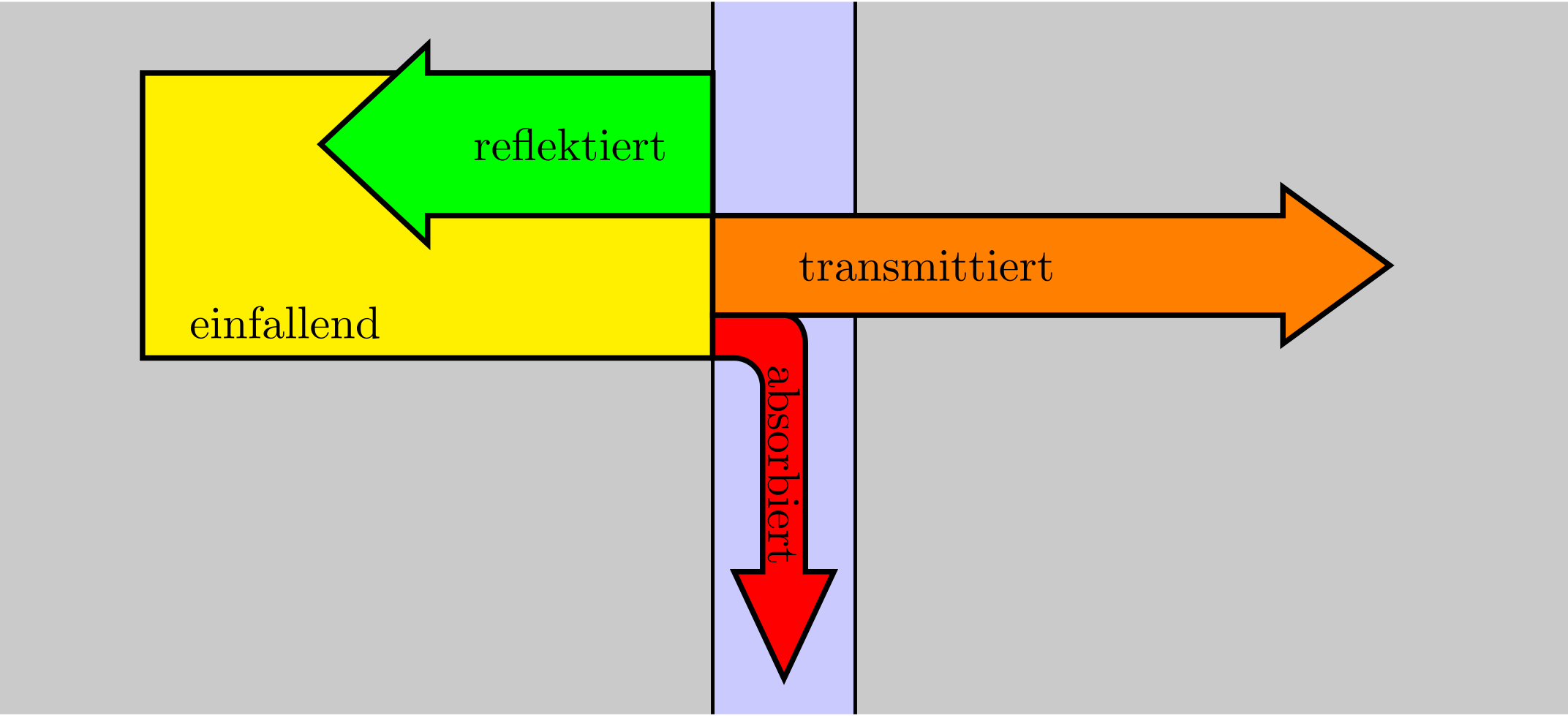
Abbildung 8.2.37: Energiebetrachtungen: Energiebilanz am Hindernis (C)
Beim Übergang einer Welle zwischen zwei Medien sind die Verhältnisse zwischen den Amplituden und Intensitäten der eingehenden, reflektierten und transmittierten Wellen interessant. Man definiert deshalb folgende Kennzahlen:
Kennzahlen
Aus der Energieerhaltung ergibt sich:
| Reflexionsfaktor | Reflexionsgrad | ||
| Transmissionsfaktor | Transmissionsgrad | ||
| Absorptionsfaktor | Absorptionsgrad |
Aus der Energieerhaltung ergibt sich:
Herleitung der allg. Formel für den Reflexionsfaktor am Bsp. einer Schallwelle
Randbedingungen an der Grenzfläche zwischen Medium 1 und 2:
| Kräftegleichgewicht links und rechts | (1) | |
| Kontinuitätsbedingung | (2) | |
| mit wird aus (2) | (3) | |
| Einsetzen der rechten Seite von (1) in (3) und Eliminieren von | ||
| Allg. Formel für den Reflexionsfaktor (gilt auch für elektromagn. Wellen) |
| für eine Schallwelle:
Schallkennimpedanz | |
| für eine elektromagn. Welle:
mit |
Reflexionsfaktor
Voraussetzung: senkrechter Einfall der Wellen ()
Voraussetzung: senkrechter Einfall der Wellen ()
| Reflexionsfaktor | Reflexionsgrad |
Beispiel
8.2.3
Eine ebene Schallwelle mit der Frequenz und dem effektiven Schalldruck breitet sich in Wasser aus und wird an der Wasseroberfläche reflektiert. Gegeben: , .
Eine ebene Schallwelle mit der Frequenz und dem effektiven Schalldruck breitet sich in Wasser aus und wird an der Wasseroberfläche reflektiert. Gegeben: , .
| a) | Wie groß ist der eff. Schalldruck und die Schallintensität der in die Luft transmittierten Welle? |
| b) | Bestimmen Sie die Schalldruckabnahme beim Übergang in . |

