4.3.1 Arbeit und Leistung
Basiswissen „Arbeit und Energie“
Die physikalischen Begriffe Arbeit, Energie und Leistung sind in unserem täglichen Wortschatz enthalten – man arbeitet, verbraucht seine Energie und bringt Leistung. Anhand eines Beispiels soll überlegt werden, was in der Physik unter diesen eigentlich abstrakten Begriffen zu verstehen ist.
Um eine schwere Last zu bewegen, muss eine Kraft angewendet werden. Soll zum Beispiel ein Baumstamm aus dem Wald gezogen werden, kann ein Pferd oder ein Traktor eingesetzt werden. Beide haben genügend Kraft dazu. Sie ziehen den Stamm mit ihrer eingesetzten Kraft entlang des Weges aus dem Wald. Man sagt, das Pferd oder der Traktor verrichten Arbeit.

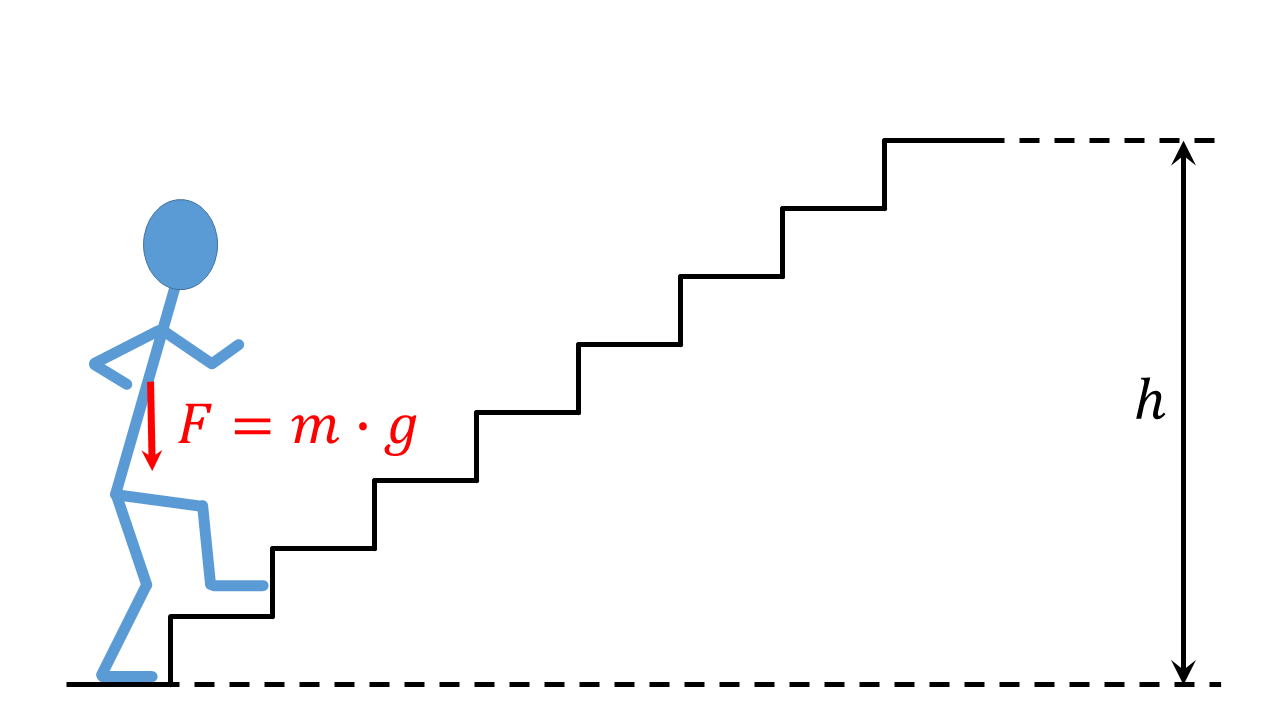
Abbildung 4.3.1: Skizze zur Arbeit (C)
Unter der Arbeit versteht man das Produkt aus Kraft und Weg:
Dabei müssen die Kraft und der Weg parallel zueinander sein.
Die Einheit der Arbeit ist das Joule: . Für das Joule gilt .
Dabei müssen die Kraft und der Weg parallel zueinander sein.
Die Einheit der Arbeit ist das Joule: . Für das Joule gilt .
Mit Energie kann Arbeit verrichtet oder Wärme erzeugt werden. Ein Körper, der Arbeit verrichtet, verringert seine Energie. Umgekehrt wächst die Energie eines Körpers, wenn an ihm Arbeit verrichtet oder ihm Wärme zugeführt wird.
Die Einheit der Energie ist .
Die Einheit der Energie ist .
Unter der Leistung wird der Quotient aus verrichteter Arbeit und dazu benötigter Zeit verstanden:
Die Einheit der Leistung ist das Watt: . Für das Watt gilt .
Die Einheit der Leistung ist das Watt: . Für das Watt gilt .
Bei Arbeit, Energie und Leistung handelt es sich um skalare Größen.
Beispiel
4.3.1
Ein schweres Kaltblut wird zum Holzrücken eingesetzt. Um einen Stamm mit einer Masse von zu ziehen, ist eine Zugkraft von nötig. Es müssen zurückgelegt werden. Die Geschwindigkeit des Pferds während des Rückens beträgt .
Wie groß ist die verrichtete Arbeit und die Leistung?
Für die Arbeit gilt:
Die Leistung ergibt sich zu:
Ein schweres Kaltblut wird zum Holzrücken eingesetzt. Um einen Stamm mit einer Masse von zu ziehen, ist eine Zugkraft von nötig. Es müssen zurückgelegt werden. Die Geschwindigkeit des Pferds während des Rückens beträgt .
Wie groß ist die verrichtete Arbeit und die Leistung?
Für die Arbeit gilt:
Die Leistung ergibt sich zu:
- Hubarbeit – wird ein Körper im Schwerefeld der Erde um eine Höhe angehoben, muss Hubarbeit verrichtet werden. Sie hängt von der Masse des Körpers und der Erdbeschleunigung ab und es gilt:
- Reibungsarbeit – wird ein Körper mit Reibung entlang einer Strecke über eine Fläche bewegt, wird Reibungsarbeit verrichtet und es gilt mit dem Reibungskoeffizienten :
- Spannarbeit – wird eine Feder mit der Federkonstanten um eine Strecke gespannt, muss Spannarbeit verrichtet werden:
- Beschleunigungsarbeit – wird ein Körper entlang einer Strecke von null auf eine Geschwindigkeit beschleunigt ergibt sich für die Beschleunigungsarbeit:
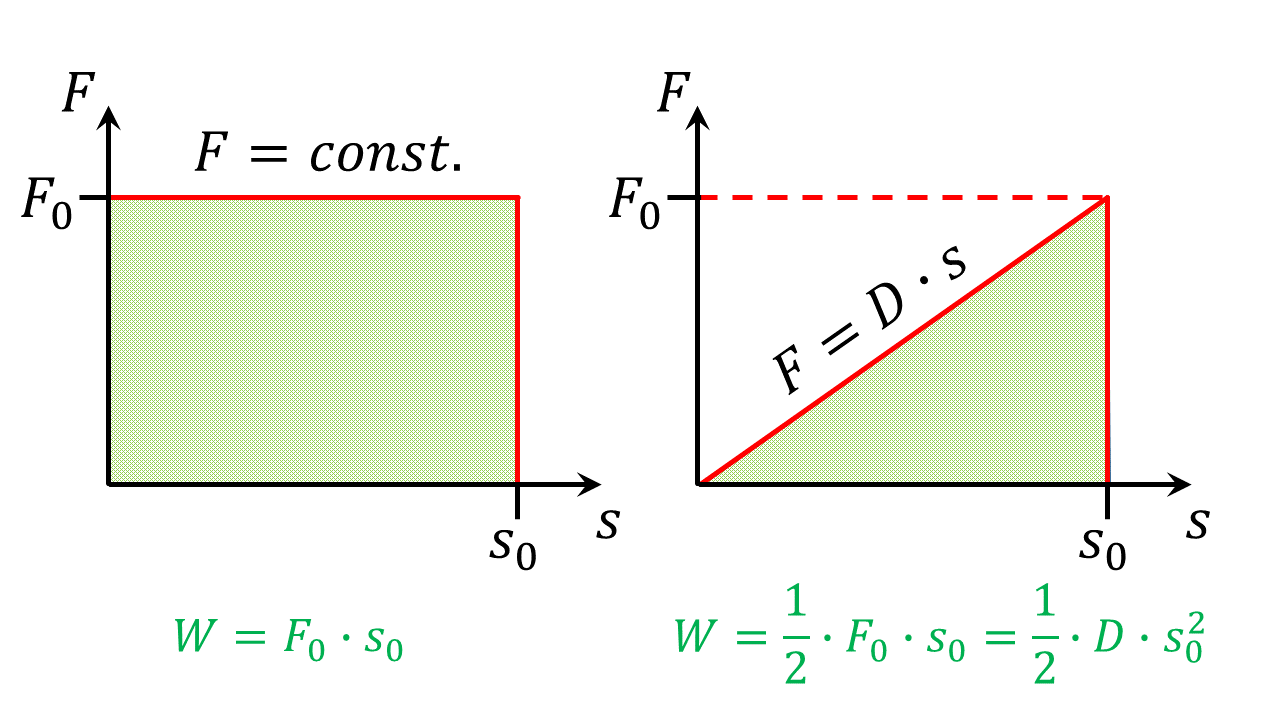
Abbildung 4.3.2: Arbeitsdiagramme bei konstanter Kraft (links) und wegabhängiger Kraft (rechts) (C)
In der Abbildung sind die Arbeitsdiagramme bei einer konstanten Kraft und einer nichtkonstanten Kraft gezeigt. Die verrichtete Arbeit entspricht den Flächen unter den Kurven. Im linken Diagramm ist die Kraft konstant. Damit kann die verrichtete Arbeit mit Hilfe des grünen Rechtecks zu bestimmt werden.
Betrachten wir das rechte Diagramm. Die Arbeit entspricht wieder der Fläche unter der Kurve. Da die Kraft aber einer Geraden mit der Steigung entspricht, lässt sich die Arbeit jetzt mit Hilfe des grünen Dreiecks bestimmen. Für die Fläche eines Dreiecks gilt GrundseiteHöhe. Es ist also .
Aufgabe 4.3.2
Arbeit ist durch definiert. Wie ändert sich die Arbeit , wenn die Kraft verfünffacht und der Weg halbiert wird?
Arbeit ist durch definiert. Wie ändert sich die Arbeit , wenn die Kraft verfünffacht und der Weg halbiert wird?
Aufgabe 4.3.3
Bei einem Wettbewerb schieben zwei Teilnehmer jeweils eine gleich schwere Kiste auf einer Strecke von . Zum Schieben ist eine Kraft von nötig. Teilnehmer benötigt und Teilnehmer benötigt nur . Es soll angenommen werden, dass die Kraft immer parallel zum Weg ist.
Wie groß ist die verrichtete Arbeit? Geben Sie das Ergebnis in an.


Wie groß ist die Leistung und der beiden Teilnehmer? Geben Sie das Ergebnis in an.


Bei einem Wettbewerb schieben zwei Teilnehmer jeweils eine gleich schwere Kiste auf einer Strecke von . Zum Schieben ist eine Kraft von nötig. Teilnehmer benötigt und Teilnehmer benötigt nur . Es soll angenommen werden, dass die Kraft immer parallel zum Weg ist.
Wie groß ist die verrichtete Arbeit? Geben Sie das Ergebnis in an.
Wie groß ist die Leistung und der beiden Teilnehmer? Geben Sie das Ergebnis in an.
Aufgabe 4.3.4
Ein Student muss zu einer Physikvorlesung in den dritten Stock des Gebäudes. Da der Aufzug kaputt ist, muss er die Treppe mit insgesamt Stufen hochsteigen. Die Stufen haben eine Höhe von . Wie groß ist die verrichtete Hubarbeit, wenn der Student eine Masse von besitzt?

Ein Student muss zu einer Physikvorlesung in den dritten Stock des Gebäudes. Da der Aufzug kaputt ist, muss er die Treppe mit insgesamt Stufen hochsteigen. Die Stufen haben eine Höhe von . Wie groß ist die verrichtete Hubarbeit, wenn der Student eine Masse von besitzt?
Aufgabe 4.3.5
Ein Auto mit der Masse erfährt eine Beschleunigung von . Wie groß ist die verrichtete Beschleunigungsarbeit, wenn der Beschleunigungsvorgang gedauert hat?

Ein Auto mit der Masse erfährt eine Beschleunigung von . Wie groß ist die verrichtete Beschleunigungsarbeit, wenn der Beschleunigungsvorgang gedauert hat?
Arbeit (!)
Video 1: Definition der Arbeit (C)
.
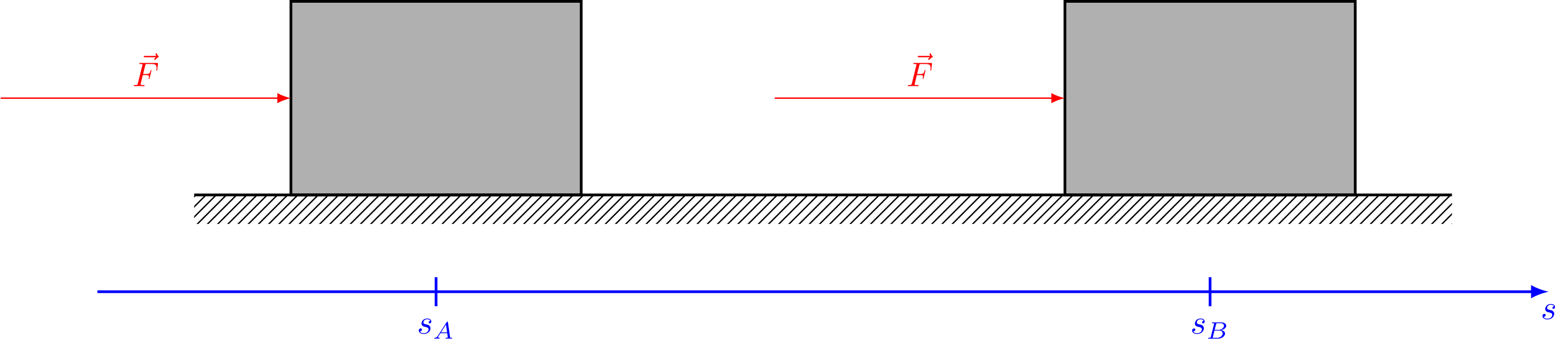
Abbildung 4.3.4: Geradlinig bewegter Körper (C)
Die Einheit der Arbeit ist .
Diese Definition der Arbeit gilt nur für Bewegungen mit einer in Betrag und Richtung konstanten Kraft, deren Vektor parallel oder antiparallel zur Bewegungsrichtung zeigt.
Video 2: Beispiel Fahrrad (C)
.
Beispiel
4.3.6
Ein Radfahrer beschleunigt auf einer Strecke von konstant von einer Geschwindigkeit auf eine Geschwindigkeit (Masse ).
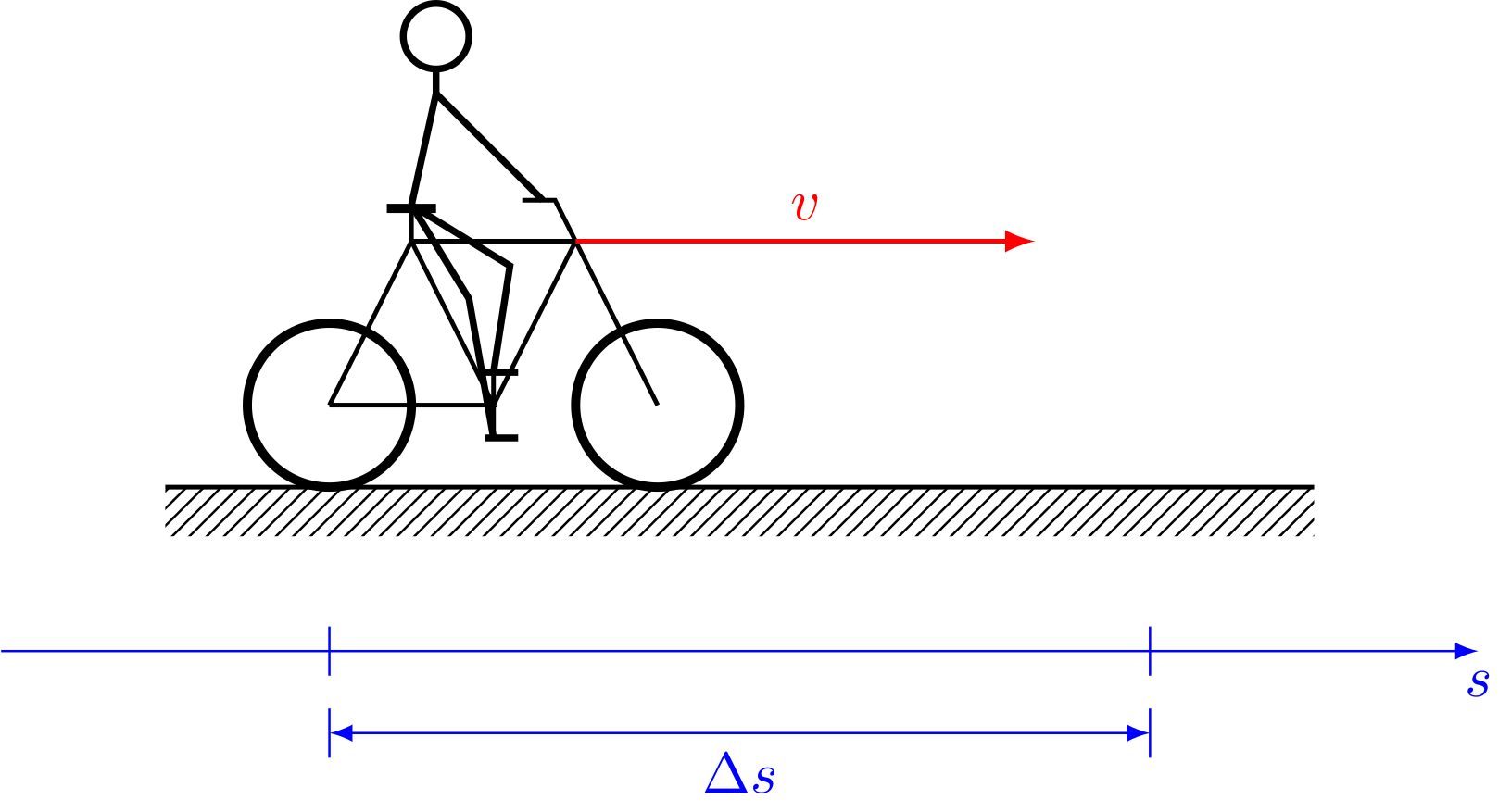
Ein Radfahrer beschleunigt auf einer Strecke von konstant von einer Geschwindigkeit auf eine Geschwindigkeit (Masse ).

Abbildung 4.3.5: Radfahrer (C)
- Wie groß ist der Betrag der Kraft, die für diese Beschleunigung nötig ist?
-
Wie groß ist die Arbeit, die durch die Kraft bei dem Beschleunigungsvorgang
verrichtet wird?
Video 3: Aufteilung in kleine Wegstücke (C)
.
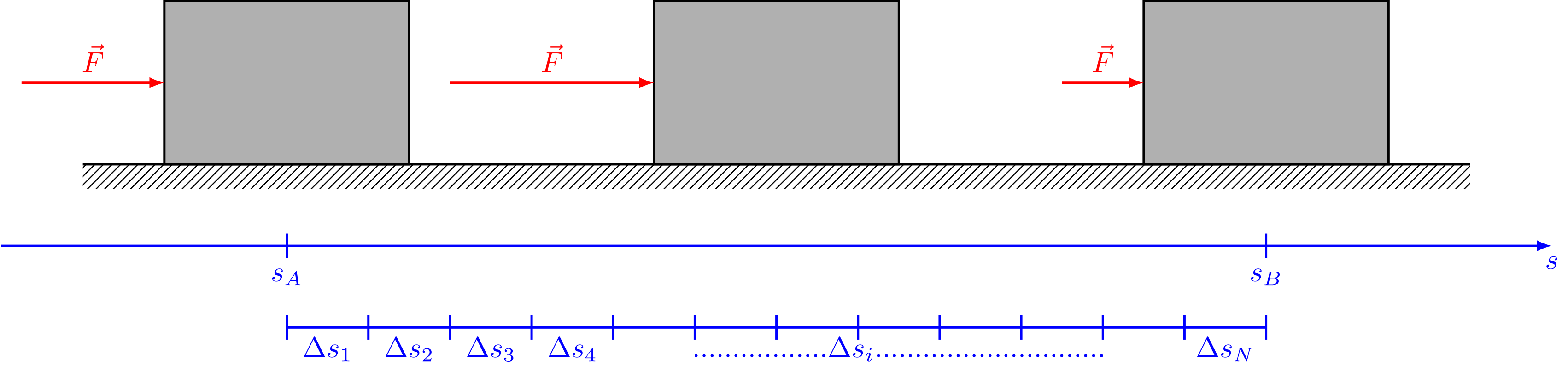
Abbildung 4.3.6: Bewegter Körper mit veränderlicher Kraft (C)
Video 4: Beispiel Auto (C)
.
Beispiel
4.3.7
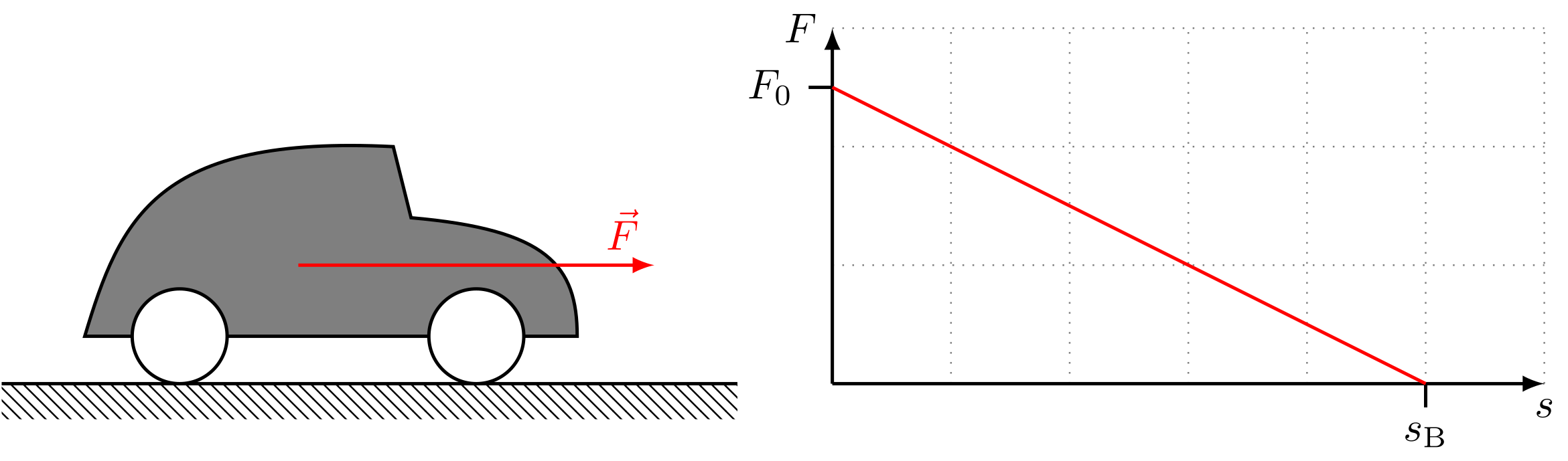
Ein Auto der Masse wird auf der Strecke aus dem Stand mit einer wegabhängigen Kraft des Betrags , , beschleunigt. Wie groß ist der Betrag der Arbeit, die während der Beschleunigung durch die Kraft verrichtet wird?

Abbildung 4.3.7: Auto wird mit wegabhängiger Kraft beschleunigt (C)
Ein Auto der Masse wird auf der Strecke aus dem Stand mit einer wegabhängigen Kraft des Betrags , , beschleunigt. Wie groß ist der Betrag der Arbeit, die während der Beschleunigung durch die Kraft verrichtet wird?
Video 5: Bewegungs- und Kraftrichtung verschieden (C)
.
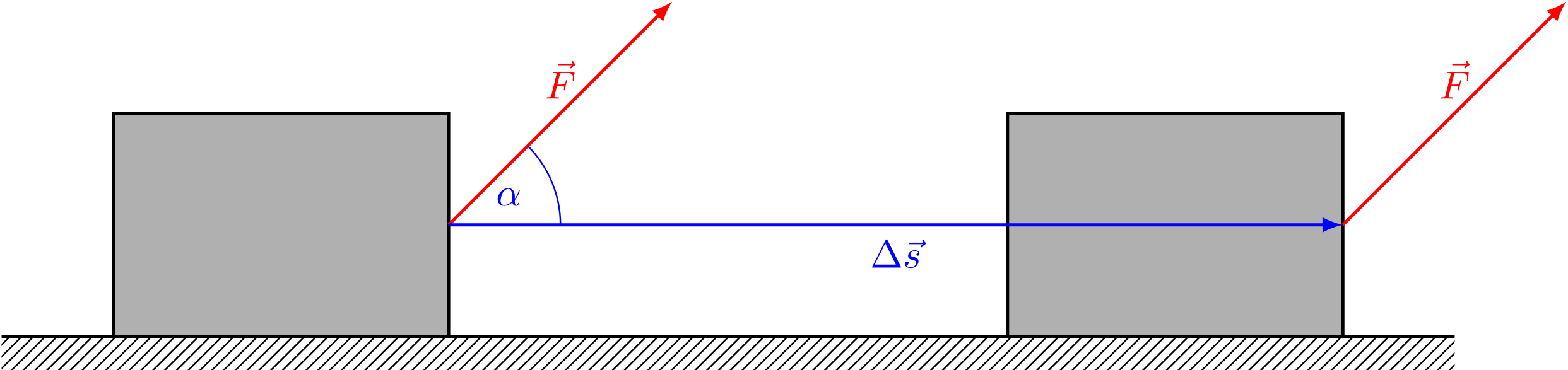
Abbildung 4.3.8: Bewegter Körper mit schräger Kraft (C)
Dabei bezeichnen den Betrag des Vektors , die Länge des Verschiebungsvektors und den Winkel zwischen der Kraftrichtung und der Bewegungsrichtung.
Video 6: Beispiel Schlitten (C)
.
Beispiel
4.3.8
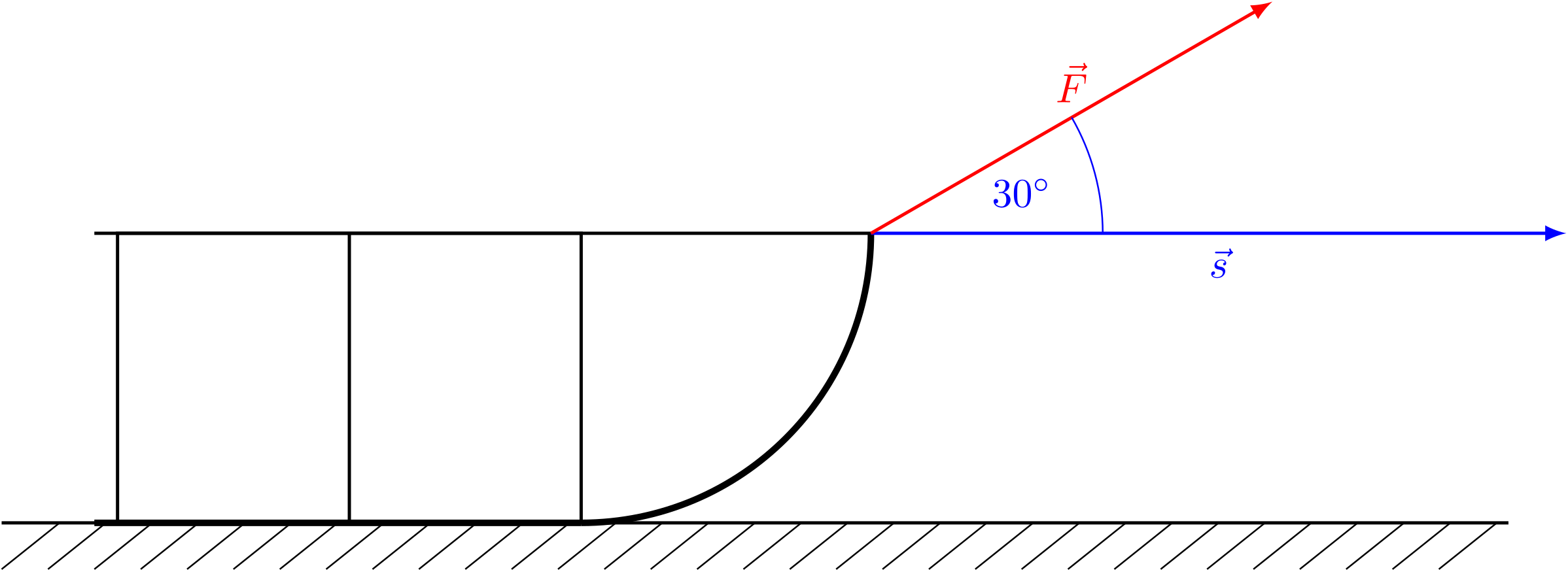
Ein Schlitten wird eine lange Straße entlang gezogen. Um die Reibung zu überwinden, muss am Zugseil, das einen Winkel von zur Straße einnimmt, mit einer Kraft von gezogen werden.
Bestimmen Sie die hierfür notwendige Arbeit.

Abbildung 4.3.9: Schlitten wird gezogen (C)
Ein Schlitten wird eine lange Straße entlang gezogen. Um die Reibung zu überwinden, muss am Zugseil, das einen Winkel von zur Straße einnimmt, mit einer Kraft von gezogen werden.
Bestimmen Sie die hierfür notwendige Arbeit.
Wir sehen uns weitere Beispiele zur Berechnung der Arbeit an:
Video 7: Beispiel Flaschenzug (C)
.
Beispiel: „Flaschenzug“
4.3.9
Hier wird ein Flaschenzug aus festen Rollen und losen Rollen betrachtet. Die Aufgabe besteht nun darin, mit diesem eine Masse um die Höhe gegen die Gewichtskraft anzuheben.
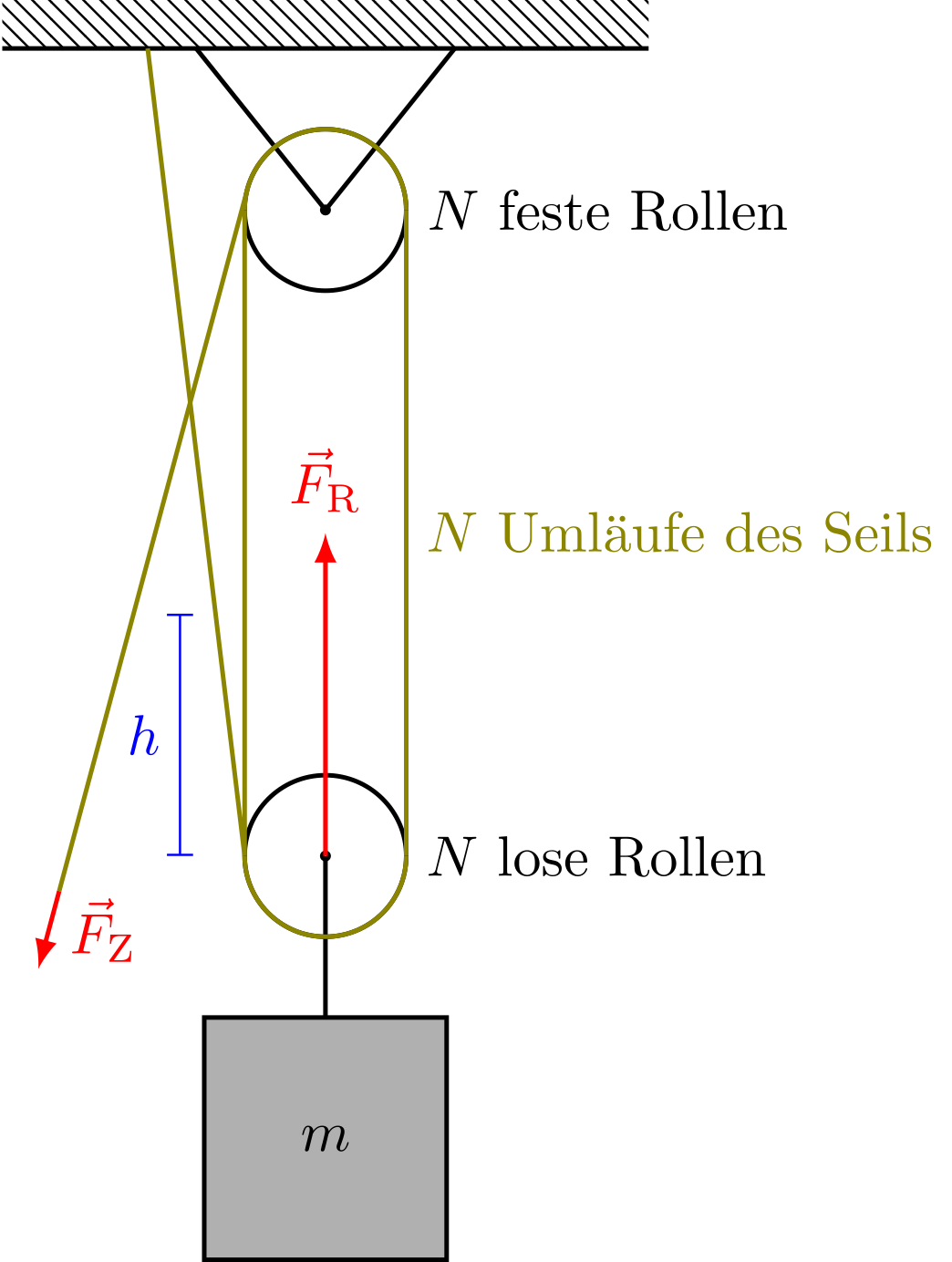
In einem vorigen Abschnitt über „Kraftwandler“ (4.1.7) wurde bereits gezeigt, dass gilt:
Die Bilanz der Arbeit führt dann auf:
Hier findet damit auch das „Goldene Gesetz der Mechanik“ Anwendung: Was man an Kraft spart, muss man an Weg zusetzen.
Hier wird ein Flaschenzug aus festen Rollen und losen Rollen betrachtet. Die Aufgabe besteht nun darin, mit diesem eine Masse um die Höhe gegen die Gewichtskraft anzuheben.

Abbildung 4.3.10: Flaschenzug (C)
In einem vorigen Abschnitt über „Kraftwandler“ (4.1.7) wurde bereits gezeigt, dass gilt:
Die Bilanz der Arbeit führt dann auf:
Hier findet damit auch das „Goldene Gesetz der Mechanik“ Anwendung: Was man an Kraft spart, muss man an Weg zusetzen.
Video 8: Beispiel Hebelgesetz (C)
.
Beispiel: „Hebelgesetz“
4.3.10
In einem vorigen Abschnitt über „Kraftwandler“ (4.1.7) wurde das Hebelgesetz bereits formuliert und angewendet.
An einer drehbar gelagerten Stange greifen in den Abständen und vom Drehpunkt tangential die Kräfte und an. Ein Beispiel hierfür wäre eine Traubenpresse, die von zwei Personen bedient wird. Die Angriffspunkte der Kräfte beschreiben Kreisbögen der Bogenlängen und . Wird der Drehwinkel in Bogenmaß angegeben, so gilt für die Bogenlänge im Abstand : .
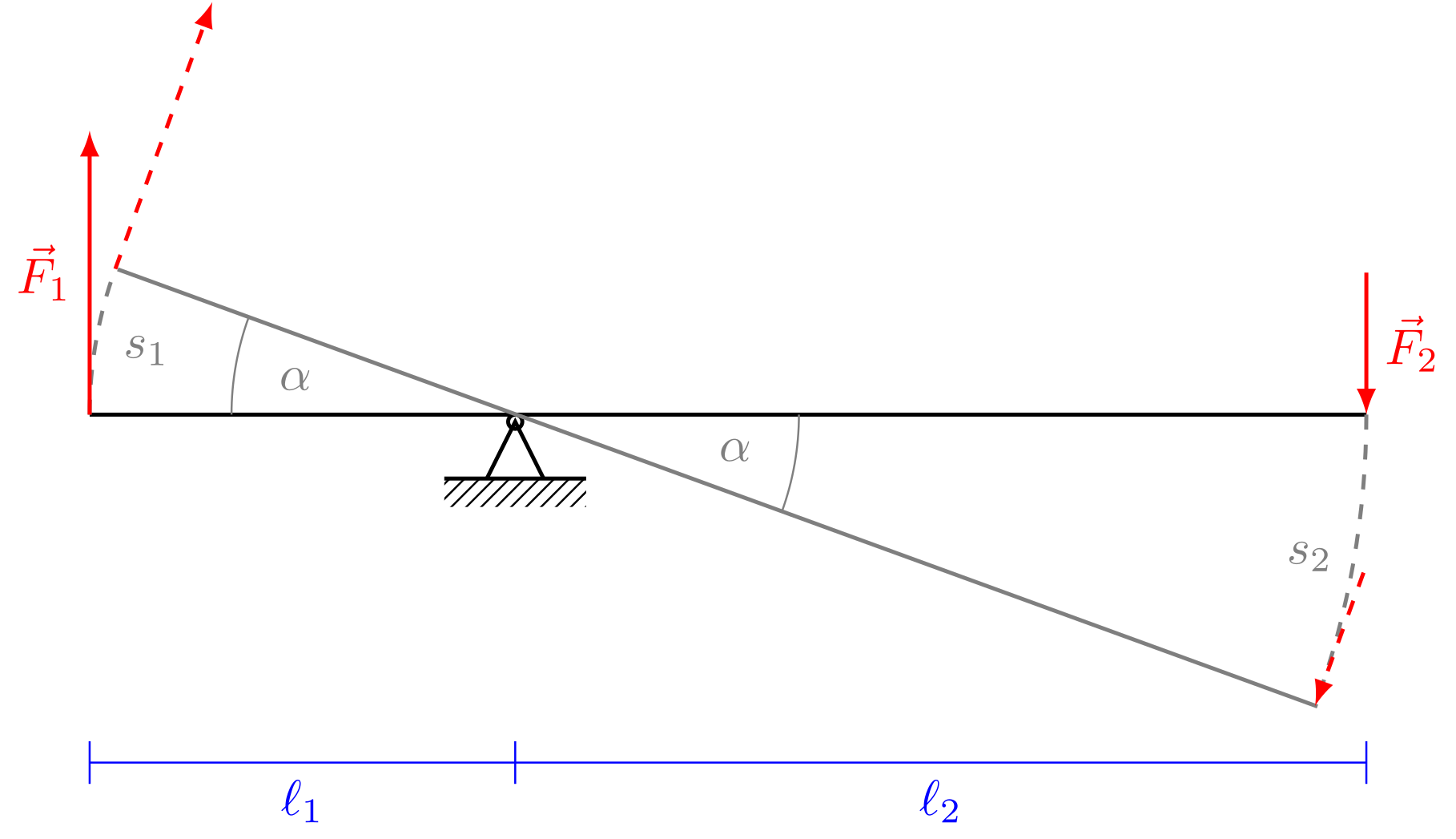
Für den Fall, dass auf beiden Seiten die gleiche Arbeit verrichtet wird, gilt
also das bereits bekannte Hebelgesetz.
In einem vorigen Abschnitt über „Kraftwandler“ (4.1.7) wurde das Hebelgesetz bereits formuliert und angewendet.
An einer drehbar gelagerten Stange greifen in den Abständen und vom Drehpunkt tangential die Kräfte und an. Ein Beispiel hierfür wäre eine Traubenpresse, die von zwei Personen bedient wird. Die Angriffspunkte der Kräfte beschreiben Kreisbögen der Bogenlängen und . Wird der Drehwinkel in Bogenmaß angegeben, so gilt für die Bogenlänge im Abstand : .

Abbildung 4.3.11: Hebelgesetz (C)
Für den Fall, dass auf beiden Seiten die gleiche Arbeit verrichtet wird, gilt
also das bereits bekannte Hebelgesetz.
Arbeit bei gekrümmtem Weg (*)
Video 9: Verallgemeinerung (C)
.
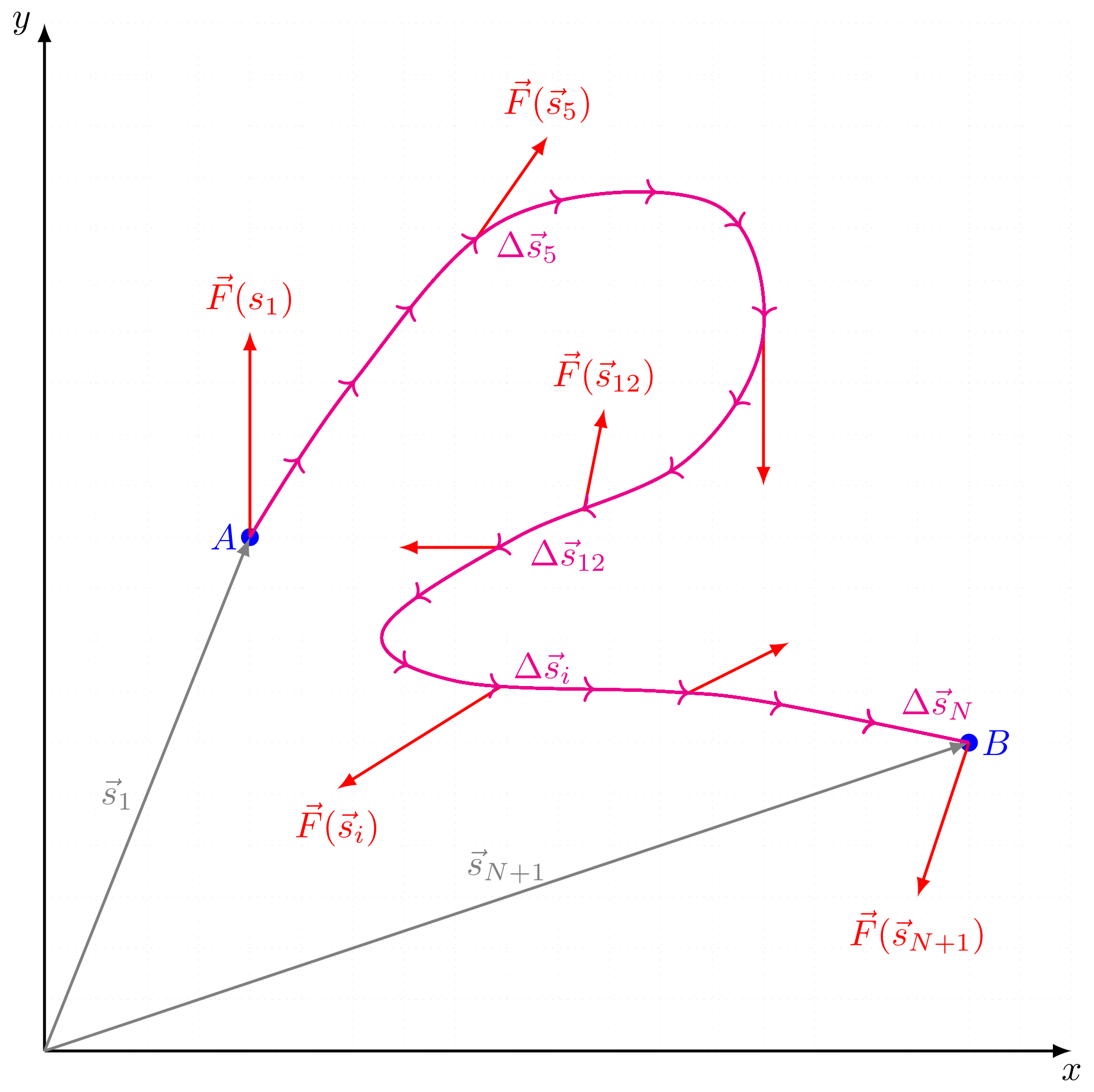
Abbildung 4.3.12: Nicht konstante Kraft in verschiedenen Richtungen (C)
Hier bezeichnet den Winkel zwischen der Kraftrichtung und der Bewegungsrichtung. Dabei kann der Winkel, da die Kraft auch in ihrer Richtung nicht konstant sein muss, von der Wegstrecke abhängen.
Weitere Erläuterungen zu der letzten Formel finden sich in dem zugehörigen Video.
Leistung (!)
Video 10: Definition Leistung (C)
.
Multipliziert man die Leistung mit einer Zeitdauer, erhält man wieder die Arbeit. Daher kann das Joule auch ausgedrückt werden als
Insbesondere in der Elektrotechnik hat man daraus eine häufig verwendete Einheit für die Arbeit abgeleitet:
Bitte achten Sie bei diesen Einheiten immer gut darauf, ob es sich um Arbeit oder Leistung handelt. Die Leistung Ihrer elektrischen Geräte ist in angegeben. Ihre Stromrechnung erhalten Sie aber für die insgesamt gelieferte Energie, also für die verbrauchten .
Video 11: Beispiel Winde 1 (C)
.
Video 12: Beispiel Winde 2 (C)
.
Beispiel
4.3.11
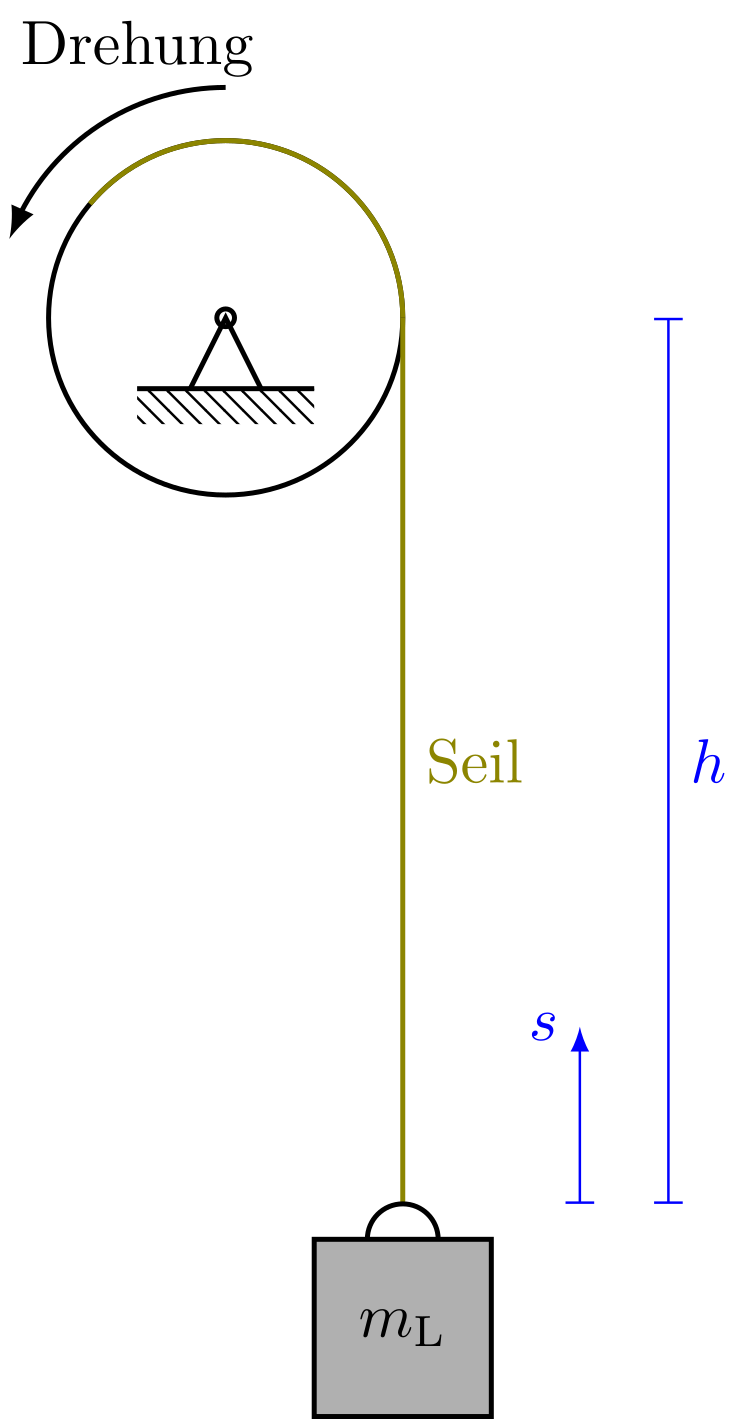
Eine Last der Masse hängt an einem Seil (Querschnitt , Dichte ) in der Tiefe . Durch Drehen einer Winde wird die Last mit konstanter Geschwindigkeit angehoben.

Abbildung 4.3.13: Last an Seilwinde (C)
Eine Last der Masse hängt an einem Seil (Querschnitt , Dichte ) in der Tiefe . Durch Drehen einer Winde wird die Last mit konstanter Geschwindigkeit angehoben.
- Berechnen Sie die durchschnittliche Leistung, die während des Hubvorgangs
aufgebracht werden muss.
-
Berechnen Sie die während des Hubvorgangs maximal nötige Leistung.
Wirkungsgrad (+)
Video 13: Wirkungsgrad (C)
.
Wird eine Maschine mit chemischer, elektrischer oder mechanischer Energie betrieben, so treten bei der Umwandlung zu der nutzbaren Energie stets Verluste auf.
Der Wirkungsgrad einer Maschine ist der Quotient aus Nutzen und Aufwand. besitzt keine Einheit, d.h. ist dimensionslos. Der Wirkungsgrad kann aus der Arbeit (nutzbare Arbeit und insgesamt zugeführte Arbeit) oder der Leistung (genutzte Leistung und Nennleistung) bestimmt werden.
Unter bestimmten Voraussetzungen gilt zusätzlich .
Unter bestimmten Voraussetzungen gilt zusätzlich .
Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie .
Falls nicht anders angegeben, verwenden Sie