4.6.3 Erzwungene Schwingung mit Dämpfung
Video 18: Erzwungene Schwingungen (C)
.
Video 19: Erzwungene Schwingungen: Einschwingvorgang (C)
.
Zusätzlich zu der Federkraft und der Dämpfung wird nun die Wirkung einer äußeren Kraft auf die Masse betrachtet. Gleichung Bewegungsgleichung (zweites Newtonsches Gesetz) muss um diesen Term erweitert werden.
Die Bewegungsgleichung für den Oszillator (hier eine Feder) mit äußerer Kraft und geschwindigkeitsproportionaler Dämpfung lautet
Division durch die Masse führt mit der Definition auf
Als einfacher Fall wird für die äußere Kraft ebenfalls eine harmonische Zeitabhängigkeit angesetzt:
Die Kreisfrequenz der Anregung ist dabei im Allgemeinen verschieden von der natürlichen Frequenz des Systems , auch Eigenfrequenz genannt. Die Phasenverschiebung erlaubt, die Phasenlage der Anregungskraft beim Zeitpunkt festzulegen. Dies ist der Zeitpunkt, zu dem typischerweise die Anfangswerte für Auslenkung und Geschwindigkeit gegeben sind. Negative Zeiten werden hier nicht betrachtet. Soll zum Beispiel ein sinusförmiger Zeitverlauf ab behandelt werden, ist einzusetzen.
Eine harmonische Bewegung der Federaufhängung wäre eine Möglichkeit eine harmonische äußere Kraft zu erzeugen. Die Auslenkung des Massenpunktes im Laborkoordinatensystem wird weiterhin mit bezeichnet. Neu ist zu spezifizieren, dass die Ruhelage des Massenpunktes definiert, wenn die Aufhängung sich in der mittleren Lage befindet. Die Auslenkung der Aufhängung in Richtung des Massenpunktes wird mit beschrieben. Damit ändert sich der Ausdruck für die rücktreibende Kraft der Feder zu . Für die äußere Kraft gilt daher
Zunächst gilt es, für die Gleichung
mit geschwindigkeitsproportionaler Dämpfung und harmonischer äußerer Kraft irgend eine Lösung zu finden. In der Mathematik wird diese eine partikuläre Lösung genannt. Hier führt der Ansatz zum Ziel, dass die Frequenz der Schwingung mit der Frequenz der Anregungskraft übereinstimmt, allerdings mit einer Phasenverschiebung gegenüber der Phase der Anregungskraft. Für die Amplitude der Auslenkung der Masse wird ein Produktansatz gewählt, bei dem die Amplitude der Anregungskraft als Proportionalitätsfaktor eingeht:
Mit der Erweiterung in die komplexen Zahlen kann verhältnismäßig einfach gezeigt werden, welche Bedingungen und erfüllen müssen, damit eine Lösung ist. Hier soll das Ergebnis ohne Herleitung angegeben werden:
mit einem Faktor und einer Phasenverschiebung , die sowohl von der Frequenz als auch von der Dämpfung abhängen. Es gilt
und
Die Lösung mit Gleichung (4.6.12) erfüllt im Allgemeinen nicht die betrachteten Anfangsbedingungen für Auslenkung und Geschwindigkeit. Sie wird jedoch als eingeschwungene Lösung bezeichnet, da Lösungen zu gegebenen Anfangsbedingungen sich exponentiell der eingeschwungenen Lösung annähern. Bevor dies am Ende des Abschnitts behandelt wird, sollen zunächst Eigenschaften von aus Gleichung (4.6.12) untersucht werden.
Die Amplitude startet bei mit dem Wert für die maximale Auslenkung der Aufhängung. Ist die Anregungsfrequenz gleich der natürlichen Frequenz verschwindet der erste Summand im Nenner. Der Fall wird Resonanzfall genannt, in dem für beliebig kleine Reibung beliebig große Amplitudenwerte erhalten werden. Diese treten in realen Systemen nicht auf, da bei entsprechend großen Amplituden Nichtlinearitäten auftreten, die gegebenenfalls mit der Zerstörung des System einhergehen. Die maximale Amplitude wird allerdings bei einer Frequenz erreicht, die etwas kleiner als die natürliche Frequenz des Oszillators ist, nämlich bei . Teilweise wird auch diese Frequenz als Resonanzfrequenz bezeichnet. Die Schwingungsamplitude geht gegen Null, wenn die Anregungsfrequenz viel größer als die natürliche Frequenz ist.
Die Phasenverschiebungen startet bei mit dem Wert Null, nimmt bei der Resonanzfrequenz den Wert an und geht gegen , wenn die Anregungsfrequenz viel größer als die Resonanzfrequenz wird. Bei dem hier gewählten Vorzeichen in bedeutet ein negativer Wert für , dass die Funktionsdarstellung von gegenüber der von zu größeren Zeiten nach rechts verschoben ist. Dies entspricht einem „Hinterherhinken“ der Schwingung gegenüber der Anregung.
Nach dieser Betrachtung der Eigenschaften der eingeschwungenen partikulären Lösung von Gleichung (4.6.10) wird abschließen auf die Erfüllung von Anfangsbedingungen eingegangen. Im vorherigen Abschnitt wurde die homogene Gleichung (4.6.1) ohne äußere Anregung analysiert. Sie wurde dort nach der höchsten Ableitung aufgelöst aufgeschrieben und wird hier in der zu Gleichung (4.6.10) analogen Schreibweise angegeben:
Die allgemeine Lösung der homogenen Gleichung (d.h. ohne Anregung) wurde in den verschiedenen Schreibweisen in Gleichungen (4.6.2) bis (4.6.4) mit bezeichnet. Aufgrund der Linearität der betrachteten Bewegungsgleichung ist ebenfalls eine Lösung der inhomogenen Gleichung:
Die Summe aus dem zweiten, vierten und sechsten Term auf der linken Seite ergibt Null, da die Lösungen der homogenen Gleichung sind. Die Summe der verbleibenden drei Terme ergibt die rechte Seite, da eine Lösung der inhomogenen Gleichung ist. In der Mathematik wird gezeigt, dass die allgemeine Lösung der inhomogenen Gleichung ist. Im Folgenden wird auf die Angabe unterschiedlicher Schreibweisen verzichtet:
mit und gemäß Gleichungen (4.6.13) und (4.6.14). Während die Frequenz der eingeschwungenen Lösung gleich der Anregungsfrequenz ist, hängt die Frequenz beim Einschwingvorgang gemäß Gleichung (4.6.5) von der natürlichen Frequenz und der Reibung ab. Die Parameter und sind durch die Anfangsbedingungen festgelegt.
Aus der Anfangsauslenkung erhält man sofort durch Einsetzen von in Gleichung (4.6.16) eine Bestimmungsgleichung für und :
Aus der Anfangsgeschwindigkeit erhält man nach Zeitableitung von Gleichung (4.6.16) und Einsetzten von die zweite Bestimmungsgleichung für und :
Löst man Gleichung (4.6.18) und Gleichung (4.6.17) nach dem Term mit auf und dividiert jeweils die linken und rechten Seiten durcheinander, erhält man die Gleichung
die nach bzw. aufgelöst werden kann.
Danach kann schließlich zum Beispiel aus
berechnet werden.
Die folgende Abbildung zeigt die Lösung für das System.
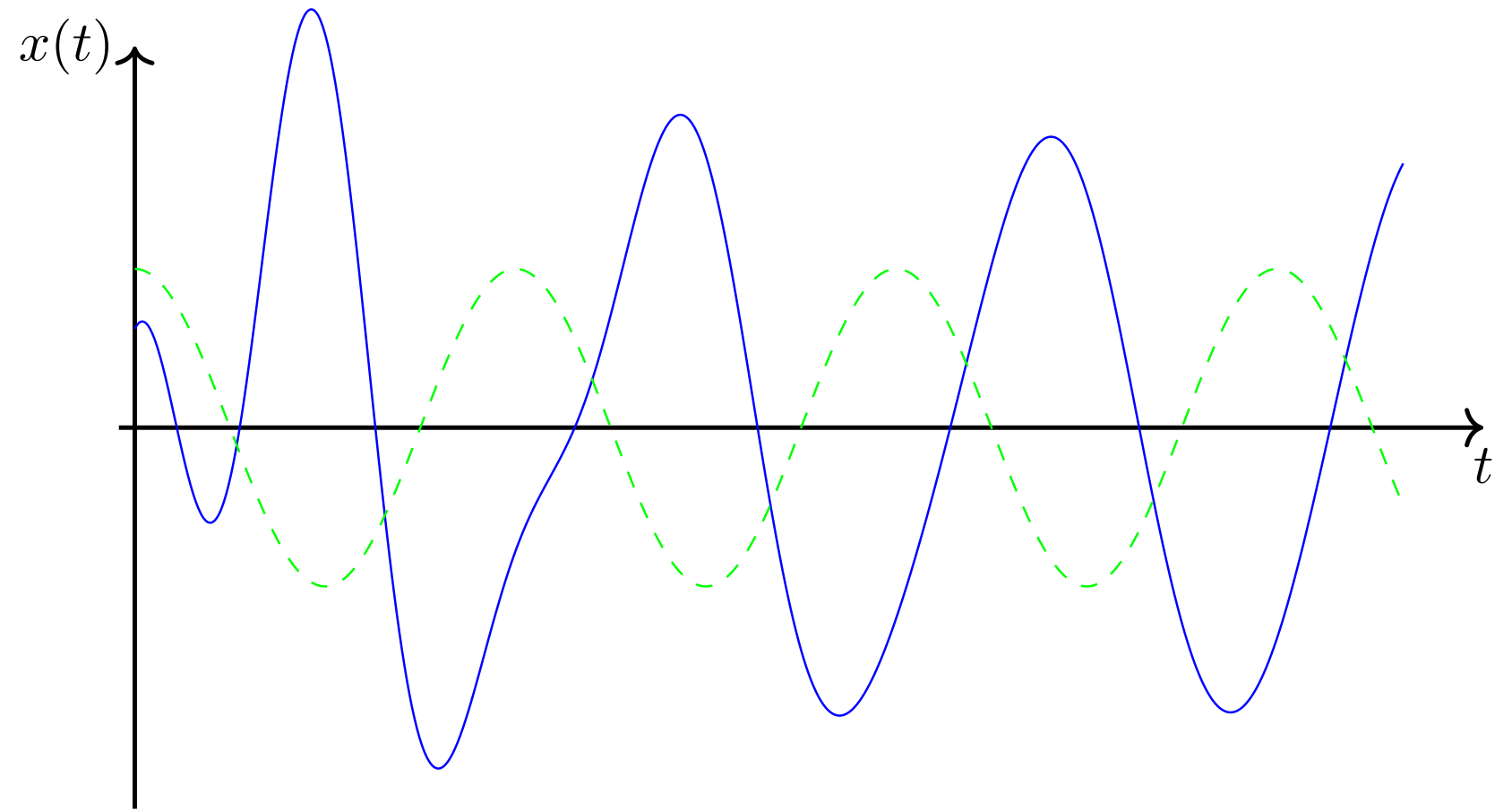
Das Hinterherhinken der Antwort gegenüber der Anregung (grün gestrichelte Kurve) ist gut zu erkennen. Während der erste positive und der erste negative Ausschlag noch kleiner als die Amplitude der eingeschwungenen Lösung sind, liegt bei dem zweiten positiven und dem zweiten negativen Ausschlag sogar ein erkennbares Überschwingen vor.
Für weniger triviale Verläufe der äußeren Kraft oder Abhängigkeiten der Reibungskraft kann kaum erwartet werden, dass die Bewegungsgleichung analytisch lösbar ist. Um den allgemeinen Fall mit bekannter äußerer Kraft oder Reibungskraft näherungsweise zu lösen, wird die Bewegungsgleichung numerisch integriert.
Die Untersuchung der einfachen linearen Gleichungen ist dennoch ein wichtiger Bestandteil des Physikstudiums. Einerseits können hier analytische Lösungen gefunden und somit Einblicke in die Zusammenhänge gewonnen werden. Andererseits lassen sich viele Phänomene näherungsweise durch lineare Gleichungen beschreiben. Viele interessante Effekte beruhen jedoch auf Nichtlinearitäten, die nicht vernachlässigt werden können.
Division durch die Masse führt mit der Definition auf
Als einfacher Fall wird für die äußere Kraft ebenfalls eine harmonische Zeitabhängigkeit angesetzt:
Die Kreisfrequenz der Anregung ist dabei im Allgemeinen verschieden von der natürlichen Frequenz des Systems , auch Eigenfrequenz genannt. Die Phasenverschiebung erlaubt, die Phasenlage der Anregungskraft beim Zeitpunkt festzulegen. Dies ist der Zeitpunkt, zu dem typischerweise die Anfangswerte für Auslenkung und Geschwindigkeit gegeben sind. Negative Zeiten werden hier nicht betrachtet. Soll zum Beispiel ein sinusförmiger Zeitverlauf ab behandelt werden, ist einzusetzen.
Eine harmonische Bewegung der Federaufhängung wäre eine Möglichkeit eine harmonische äußere Kraft zu erzeugen. Die Auslenkung des Massenpunktes im Laborkoordinatensystem wird weiterhin mit bezeichnet. Neu ist zu spezifizieren, dass die Ruhelage des Massenpunktes definiert, wenn die Aufhängung sich in der mittleren Lage befindet. Die Auslenkung der Aufhängung in Richtung des Massenpunktes wird mit beschrieben. Damit ändert sich der Ausdruck für die rücktreibende Kraft der Feder zu . Für die äußere Kraft gilt daher
Zunächst gilt es, für die Gleichung
mit geschwindigkeitsproportionaler Dämpfung und harmonischer äußerer Kraft irgend eine Lösung zu finden. In der Mathematik wird diese eine partikuläre Lösung genannt. Hier führt der Ansatz zum Ziel, dass die Frequenz der Schwingung mit der Frequenz der Anregungskraft übereinstimmt, allerdings mit einer Phasenverschiebung gegenüber der Phase der Anregungskraft. Für die Amplitude der Auslenkung der Masse wird ein Produktansatz gewählt, bei dem die Amplitude der Anregungskraft als Proportionalitätsfaktor eingeht:
Mit der Erweiterung in die komplexen Zahlen kann verhältnismäßig einfach gezeigt werden, welche Bedingungen und erfüllen müssen, damit eine Lösung ist. Hier soll das Ergebnis ohne Herleitung angegeben werden:
mit einem Faktor und einer Phasenverschiebung , die sowohl von der Frequenz als auch von der Dämpfung abhängen. Es gilt
und
Die Lösung mit Gleichung (4.6.12) erfüllt im Allgemeinen nicht die betrachteten Anfangsbedingungen für Auslenkung und Geschwindigkeit. Sie wird jedoch als eingeschwungene Lösung bezeichnet, da Lösungen zu gegebenen Anfangsbedingungen sich exponentiell der eingeschwungenen Lösung annähern. Bevor dies am Ende des Abschnitts behandelt wird, sollen zunächst Eigenschaften von aus Gleichung (4.6.12) untersucht werden.
Beispiel
4.6.13
In der folgenden Abbildung ist die Amplitude in Gl. (4.6.12) für das Beispielmodell als Funktion der Frequenz dargestellt. Dabei wurde wiederum für der Einheitswert von eingesetzt.
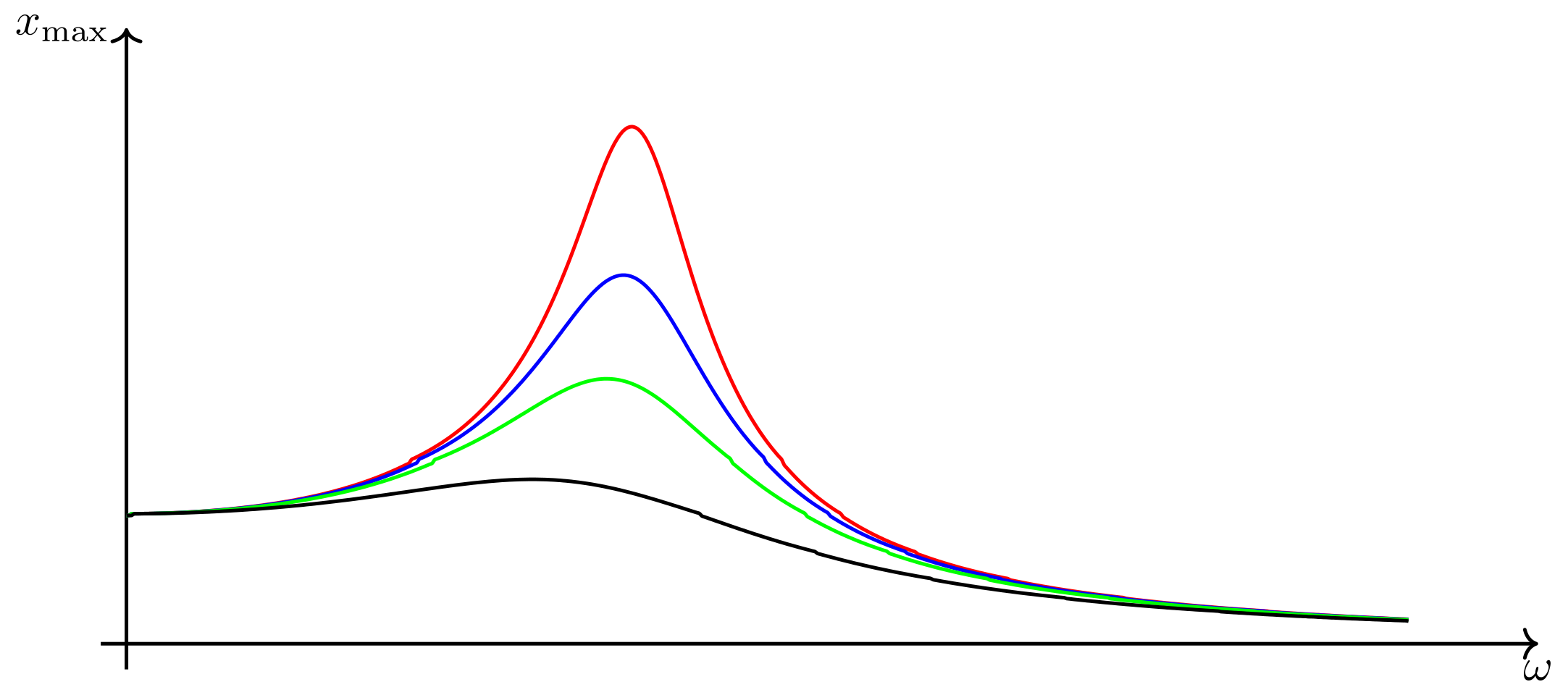
Bei der Berechnung von kann und genutzt werden.
Einsetzen der natürlichen Kreisfrequenz als Kreisfrequenz der anregenden Kraft liefert für die Amplitude. Das Verhältnis sinkt mit zunehmender Dämpfung. Im Beispielmodell beträgt es Eins, was einer starken Dämpfung entspricht.
In der folgenden Abbildung ist die Amplitude in Gl. (4.6.12) für das Beispielmodell als Funktion der Frequenz dargestellt. Dabei wurde wiederum für der Einheitswert von eingesetzt.

Abbildung 4.6.78: Amplitude über der Frequenz (C)
Bei der Berechnung von kann und genutzt werden.
Einsetzen der natürlichen Kreisfrequenz als Kreisfrequenz der anregenden Kraft liefert für die Amplitude. Das Verhältnis sinkt mit zunehmender Dämpfung. Im Beispielmodell beträgt es Eins, was einer starken Dämpfung entspricht.
Die Amplitude startet bei mit dem Wert für die maximale Auslenkung der Aufhängung. Ist die Anregungsfrequenz gleich der natürlichen Frequenz verschwindet der erste Summand im Nenner. Der Fall wird Resonanzfall genannt, in dem für beliebig kleine Reibung beliebig große Amplitudenwerte erhalten werden. Diese treten in realen Systemen nicht auf, da bei entsprechend großen Amplituden Nichtlinearitäten auftreten, die gegebenenfalls mit der Zerstörung des System einhergehen. Die maximale Amplitude wird allerdings bei einer Frequenz erreicht, die etwas kleiner als die natürliche Frequenz des Oszillators ist, nämlich bei . Teilweise wird auch diese Frequenz als Resonanzfrequenz bezeichnet. Die Schwingungsamplitude geht gegen Null, wenn die Anregungsfrequenz viel größer als die natürliche Frequenz ist.
Beispiel
4.6.14
Die folgende Abbildung zeigt die Phasenverschiebung für das Beispielmodell als Funktion der Frequenz.
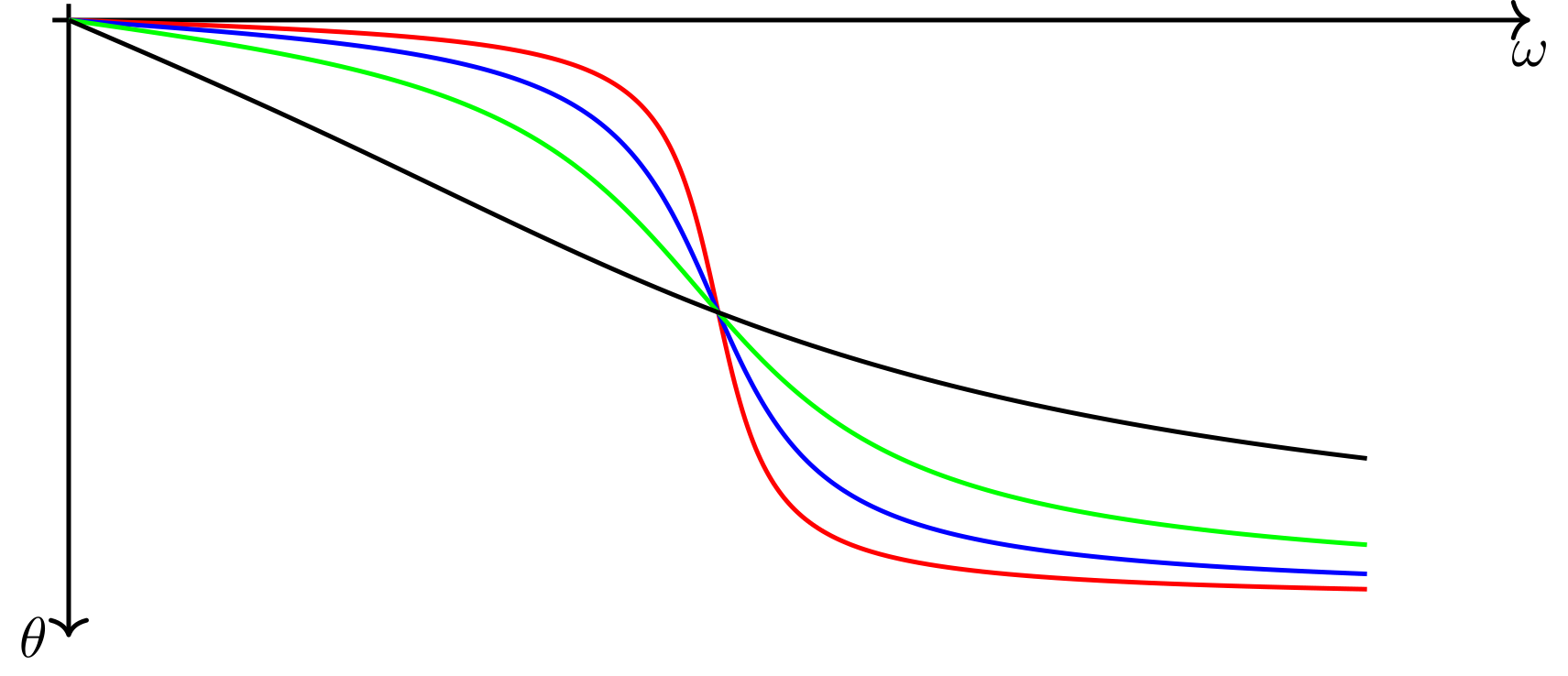
Die folgende Abbildung zeigt die Phasenverschiebung für das Beispielmodell als Funktion der Frequenz.

Abbildung 4.6.79: Phasenverschiebung über der Frequenz (C)
Die Phasenverschiebungen startet bei mit dem Wert Null, nimmt bei der Resonanzfrequenz den Wert an und geht gegen , wenn die Anregungsfrequenz viel größer als die Resonanzfrequenz wird. Bei dem hier gewählten Vorzeichen in bedeutet ein negativer Wert für , dass die Funktionsdarstellung von gegenüber der von zu größeren Zeiten nach rechts verschoben ist. Dies entspricht einem „Hinterherhinken“ der Schwingung gegenüber der Anregung.
Nach dieser Betrachtung der Eigenschaften der eingeschwungenen partikulären Lösung von Gleichung (4.6.10) wird abschließen auf die Erfüllung von Anfangsbedingungen eingegangen. Im vorherigen Abschnitt wurde die homogene Gleichung (4.6.1) ohne äußere Anregung analysiert. Sie wurde dort nach der höchsten Ableitung aufgelöst aufgeschrieben und wird hier in der zu Gleichung (4.6.10) analogen Schreibweise angegeben:
Die allgemeine Lösung der homogenen Gleichung (d.h. ohne Anregung) wurde in den verschiedenen Schreibweisen in Gleichungen (4.6.2) bis (4.6.4) mit bezeichnet. Aufgrund der Linearität der betrachteten Bewegungsgleichung ist ebenfalls eine Lösung der inhomogenen Gleichung:
Die Summe aus dem zweiten, vierten und sechsten Term auf der linken Seite ergibt Null, da die Lösungen der homogenen Gleichung sind. Die Summe der verbleibenden drei Terme ergibt die rechte Seite, da eine Lösung der inhomogenen Gleichung ist. In der Mathematik wird gezeigt, dass die allgemeine Lösung der inhomogenen Gleichung ist. Im Folgenden wird auf die Angabe unterschiedlicher Schreibweisen verzichtet:
mit und gemäß Gleichungen (4.6.13) und (4.6.14). Während die Frequenz der eingeschwungenen Lösung gleich der Anregungsfrequenz ist, hängt die Frequenz beim Einschwingvorgang gemäß Gleichung (4.6.5) von der natürlichen Frequenz und der Reibung ab. Die Parameter und sind durch die Anfangsbedingungen festgelegt.
Aus der Anfangsauslenkung erhält man sofort durch Einsetzen von in Gleichung (4.6.16) eine Bestimmungsgleichung für und :
Aus der Anfangsgeschwindigkeit erhält man nach Zeitableitung von Gleichung (4.6.16) und Einsetzten von die zweite Bestimmungsgleichung für und :
Löst man Gleichung (4.6.18) und Gleichung (4.6.17) nach dem Term mit auf und dividiert jeweils die linken und rechten Seiten durcheinander, erhält man die Gleichung
die nach bzw. aufgelöst werden kann.
Danach kann schließlich zum Beispiel aus
berechnet werden.
Die folgende Abbildung zeigt die Lösung für das System.

Abbildung 4.6.80: Zeitverlauf einer erzwungenen Schwingung (C)
Das Hinterherhinken der Antwort gegenüber der Anregung (grün gestrichelte Kurve) ist gut zu erkennen. Während der erste positive und der erste negative Ausschlag noch kleiner als die Amplitude der eingeschwungenen Lösung sind, liegt bei dem zweiten positiven und dem zweiten negativen Ausschlag sogar ein erkennbares Überschwingen vor.
Für weniger triviale Verläufe der äußeren Kraft oder Abhängigkeiten der Reibungskraft kann kaum erwartet werden, dass die Bewegungsgleichung analytisch lösbar ist. Um den allgemeinen Fall mit bekannter äußerer Kraft oder Reibungskraft näherungsweise zu lösen, wird die Bewegungsgleichung numerisch integriert.
Die Untersuchung der einfachen linearen Gleichungen ist dennoch ein wichtiger Bestandteil des Physikstudiums. Einerseits können hier analytische Lösungen gefunden und somit Einblicke in die Zusammenhänge gewonnen werden. Andererseits lassen sich viele Phänomene näherungsweise durch lineare Gleichungen beschreiben. Viele interessante Effekte beruhen jedoch auf Nichtlinearitäten, die nicht vernachlässigt werden können.

