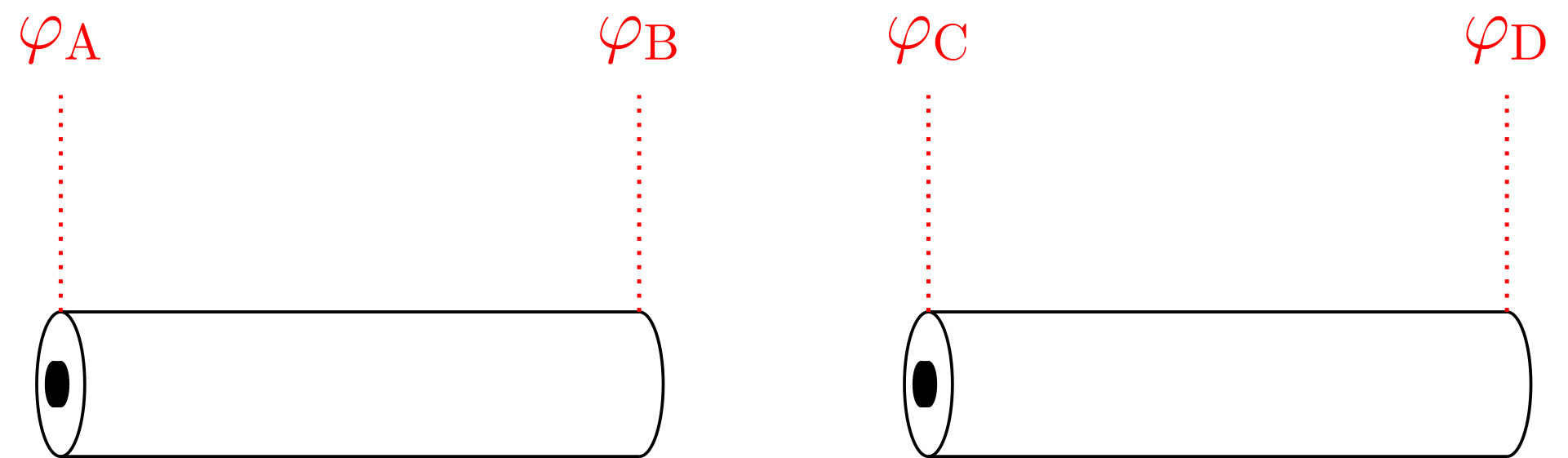
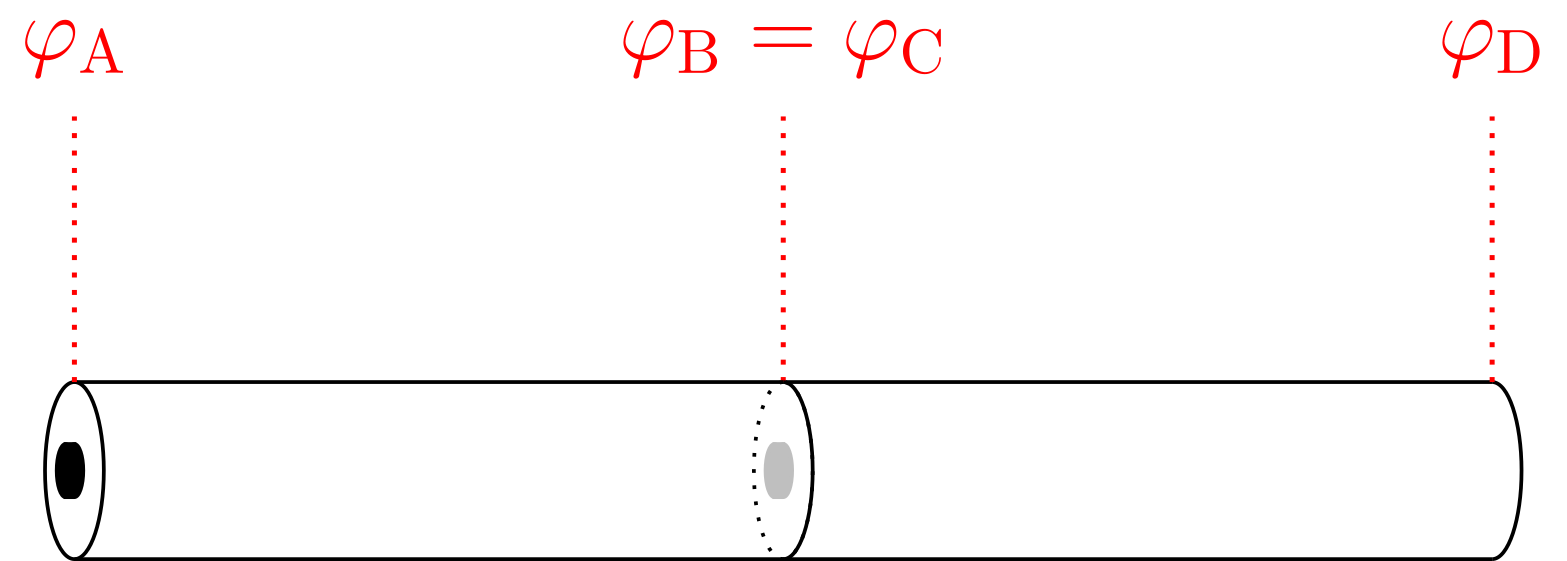2. Elektromagnetismus
  3. Elektrostatik
  4. Arbeit, Potential, Spannung (!),(*)

5.1.3 Elektrische Arbeit, Potential und Spannung





 

Basiswissen – Äquipotentialflächen


In der Physik wird oftmals von sogenannten Äquipotentialflächen gesprochen. Darunter versteht man Flächen, auf denen die Feldstärke und somit die auf einen Körper wirkende Kraft senkrecht steht, sich also die potentielle Energie des Körpers bei Verschiebung auf dieser Fläche nicht ändert. Im Gravitationsfeld der Erde entsprechen solche Äquipotentialflächen Flächen mit gleicher Höhe. Sie sind in Landkarten als Höhenlinien zu finden. Bewegt sich eine Masse entlang einer solchen Höhenlinie, wird keine Hubarbeit verrichtet. Dieses Prinzip kann so auch auf elektrostatische Felder übertragen werden.
Beim elektrischen Feld einer Punktladung liegen diese Äquipotentialflächen auf konzentrischen Kugeloberflächen mit der Punktladung als Mittelpunkt. Auf diesen Flächen ist der Betrag der elektrischen Feldstärke konstant und damit ist der Betrag der anziehenden oder abstoßenden Kraft auf eine Probeladung, unabhängig davon, wo sie sich auf der Äquipotentialfläche befindet, immer gleich groß. Wird eine Probeladung auf einer solchen Fläche bewegt, muss keine elektrische Arbeit verrichtet werden.
In der folgenden Skizze sind verschiedene Äquipotentialflächen einer Punktladung Q rot gezeichnet. Für das Potential wird üblicherweise als Symbol der griechische Buchstaben φ benutzt. Je größer der Abstand von der Punktladung ist, desto schwächer ist das elektrische Feld, dessen Richtung und Betrag durch die blauen Pfeile dargestellt ist.

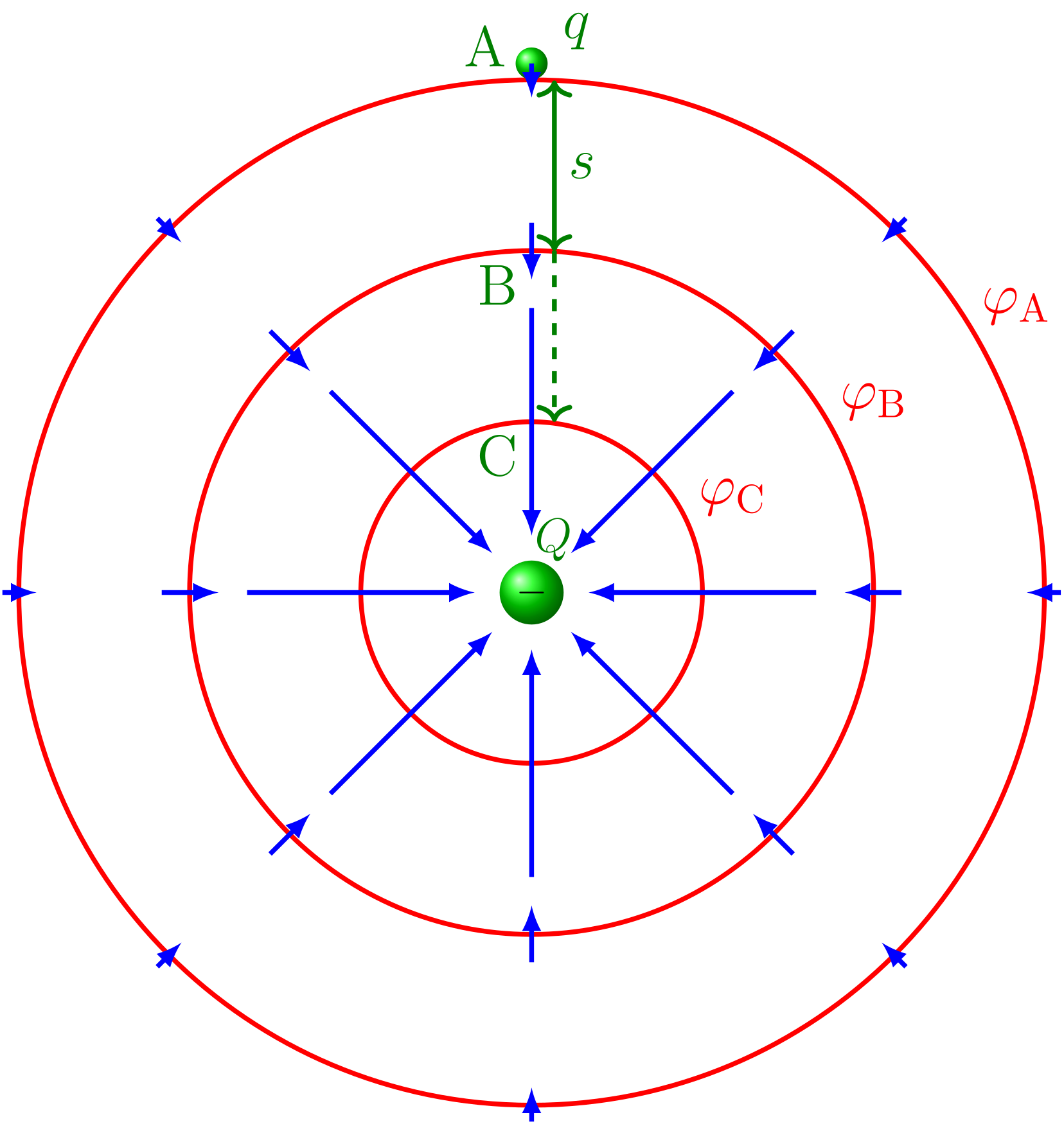
./_D4FEFF6D_4x.png
Abbildung 5.1.75: Äquipotentiallinien und Feldvektoren einer elektrischen Punktladung  (C)

Elektrische Feldlinien stehen immer senkrecht auf den zugehörigen Äquipotentialflächen.


 

Basiswissen – Potential, Arbeit, Spannung


In der obigen Zeichnung sind verschiedene Äquipotentialflächen, die durch die Potentiale φ A , φ B und φ C gekennzeichnet sind, eingezeichnet. Um eine Probeladung q von einem beliebigen festen Punkt, dem Bezugspunkt, an die Position A im elektrischen Feld E → zu bringen, muss Arbeit W A verrichtet werden.
Der Quotient aus der Arbeit W A und der Ladung q wird als Potential φ A bezeichnet:

φ A = W A q  .

Dabei ist W A die Arbeit, die aufgewendet werden muss, um die Ladung q im elektrischen Feld E → an die Position A zu bringen.
Oder anders formuliert, gibt das Potential φ A an, welche Energie die Ladung q gegenüber dem Bezugspunkt hat.
Die Einheit des Potentials ist [ φ A ]=V (Volt).
Die Punkte B und C befinden sich auf anderen Äquipotentialflächen. Um eine Ladung q vom Bezugspunkt auf eine dieser Fläche zu bringen, muss die Arbeit W B oder W C aufgebracht werden. Um die Probeladung q nun vom Punkt A nach B zu bringen, muss die Arbeit W A → B aufgebracht werden. Diese ergibt sich als Differenz der Arbeiten W A und W B :

W A → B = W B - W A  .

Dabei wird die Potentialdifferenz zwischen Punkt A und B überwunden:

Δ φ A → B = φ B - φ A  .

Liegen zwei Punkte A und B auf zwei verschiedenen Äquipotentialflächen, nennt man die Potentialdifferenz zwischen φ A und φ B elektrische Spannung U:

U= φ A - φ B  .

Die Einheit der Spannung ist [U]=V.


Das elektrische Feld und damit das Potential hängen von der Ladungsverteilung im Raum ab. Für den einfachen Fall der elektrischen Punktladung Q verändert sich das Potential mit dem Abstand r von der Ladung und das Potential lässt sich einfach beschreiben.

  • Für das Potential in der Umgebung einer Punktladung Q gilt:

    φ(r)= 1 4·π· ε0 · Q r  .



  • Das Potential hängt, im Fall der punktförmigen Ladung, neben den konstanten Faktoren nur von der Ladung Q und dem Abstand r zur Ladung ab.

  • Das Potential nimmt mit zunehmendem Abstand r von der Ladung Q ab.

  • Die Einheit des Potentials ist: [φ]= J C =V (Volt).

  • Bei der Bewegung einer Probeladung auf einer Äquipotentialfläche wird keine elektrische Arbeit verrichtet.

Um die Arbeit zu berechnen, die benötigt wird, um eine Probeladung in einem elektrischen Feld an eine Stelle A zu bringen, müssen sogenannte Wegintegrale gelöst werden. An dieser Stelle wird auf die Berechnung der Arbeit im elektrischen Feld verzichtet und auf den Lektionstext verwiesen.


Aufgabe 5.1.31  
Wir betrachten eine Fläche, auf der das elektrische Potential konstant ist. Welche der Aussagen ist für diese Fläche richtig?
 
Das elektrische Feld ist auf einer solchen Fläche immer Null.
Zwischen verschiedenen Punkten auf der Fläche ist die Spannung immer Null.
Zwischen verschiedenen Punkten auf der Fläche liegt eine Spannung an.
Der elektrische Feldvektor steht senkrecht auf der Äquipotentialfläche.
 


Aufgabe 5.1.32  
Sie müssen die Batterien in der Fernbedienung Ihres Fernsehers austauschen. Dazu benötigen Sie handelsübliche Batterien vom Typ R03 (AAA). Die Nennspannung einer neuen Batterie liegt bei 1,5 V. Welche Spannung liegt an, wenn Sie zwei Batterien in folgender Form in die Fernbedienung einbauen:

./_2162D6DD_4x.png
Abbildung 5.1.76: Skizze Batterien  (C)

U  = 




Aufgabe 5.1.33  
Ein Elektron bewegt sich im Vakuum von einem Punkt A zu einem Punkt B . Zwischen den beiden Punkten besteht eine Potentialdifferenz von U=+5000 V. Welche Geschwindigkeit v erreicht das Elektron, wenn es aus der Ruhe startet?
Rechnen sie mit q e =-1,6· 10-19  C für die Ladung und m e =9,1· 10-31  kg für die Masse des Elektrons.
 
Geben Sie das Ergebnis auf zwei signifikante Stellen genau an.

v  =  E 




Aufgabe 5.1.34  
Die Erde besitzt neben dem Gravitationsfeld auch ein elektrostatisches Feld. Das elektrostatische Feld ist wie das Gravitationsfeld zum Erdmittelpunkt gerichtet.
Welche Geschwindigkeit erreicht ein punktförmiger Körper, wenn er aus der Ruhe h=2 m fällt?
Berechnen Sie die Geschwindigkeit v u für einen ungeladenen Körper und diejenige für einen geladenen Körper, v g . Beide Körper haben die Masse m=0,54 kg. Der geladene Körper trägt die Ladung q=+550· 10-6  C. Für das elektrostatische Feld gilt in der Nähe der Erdoberfläche etwa E=150  V m .

Die Reibung durch Luft ist zu vernachlässigen. Denken Sie daran, dass für die Arbeit W gilt:

W=F·s .

Geben Sie das Ergebnis jeweils auf drei signifikante Stellen genau an.

v u  = 
 
v g  = 






Video 19: Arbeit, Energie und Potential im elektrischen Feld, Teil 1 (C) .



 

Arbeit, Energie und Potential im elektrischen Feld (!)


Aus der Mechanik ist bekannt, dass Arbeit verrichtet wird, wenn man einen Körper von der Erdoberfläche aus nach oben transportiert, denn man muss die zwischen Erde und Körper wirkende Gravitationskraft überwinden. Gleichzeitig wird beim Anheben auch die potentielle Energie E pot (in der Schule gerne als Lageenergie bezeichnet) des Körpers erhöht.

Dieser Zusammenhang gilt auch für die Bewegung einer Ladung in einem elektrischen Feld. Bewegt man eine Probeladung q in einem E → -Feld gegen die elektrische Kraft, so muss man ebenfalls Arbeit verrichten.

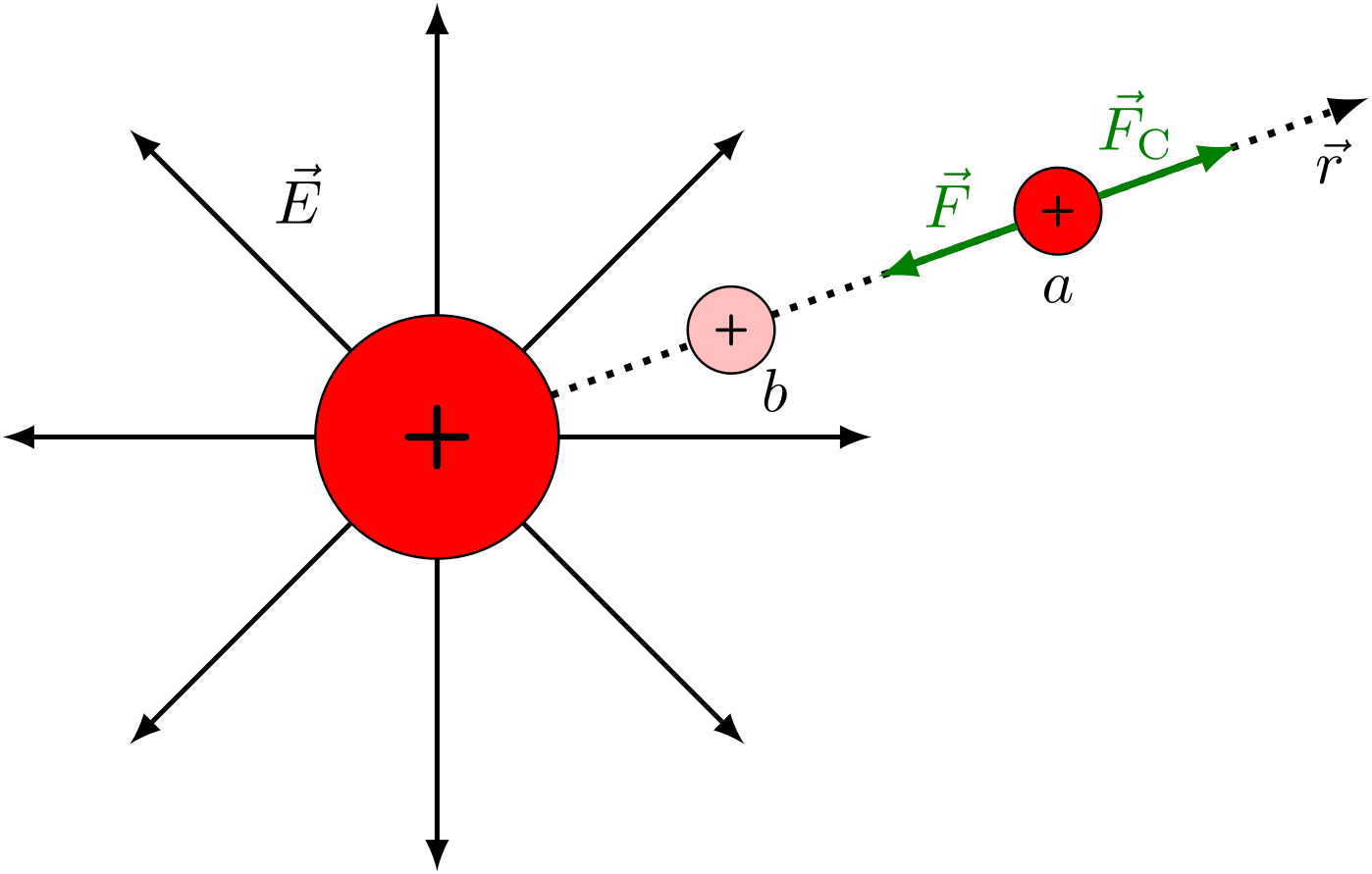
./_DB916447_4x.png
Abbildung 5.1.79: Probeladung im elektrischen Feld einer gleichnamigen Ladung  (C)



Arbeit zum Verschieben der positiven Ladung von a nach b:
 
W  =  ∫ r → a r → b F → ·d s →   =  ∫ r → a r → b (- F → C )·d s →   = - ∫ r → a r → b q E → ·d s →   =  E pot ( r → b )- E pot ( r → a ) .
 
Bringt man die Ladung aus dem Unendlichen, so ergibt sich für das Integral entlang eines radialen Strahls
 
W  = -q ∫∞ r E ds   = -q ∫∞ r 1 4π ε0   Q s2  ds   = q [ 1 4π ε0   Q s ]∞ r   = q 1 4π ε0   Q r -0 .
 
Daraus ergibt sich für die potentielle Energie am Ort r → :
Potentielle Energie  


E pot ( r → )=q 1 4π ε0   Q r  .



Video 20: Arbeit, Energie und Potential im elektrischen Feld, Teil 2 (C) .



Die potentielle Energie der Ladung q am Ort r → ist abhängig vom Feld und von der Ladung q selbst. Teilt man die potentielle Energie durch die Ladung wird der Ausdruck unabhängig von q und man erhält das nur vom elektrischen Feld abhängige Potential φ( r → ):
Elektrisches Potential  


φ( r → )= E pot ( r → ) q =- ∫∞ r E ds .



In der folgenden Simulation kann die Größe einer Punktladung Q eingestellt werden. Es werden dabei die elektrische Feldstärke E und das elektrische Potential φ in Abhängigkeit des Abstandes r von der Ladung dargestellt.

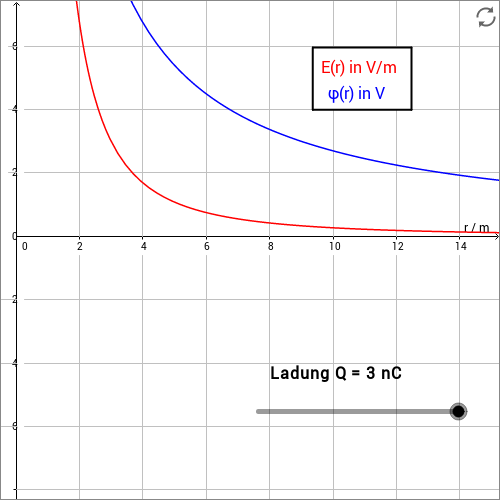
././Physikkurs/elektrisch_spannungpotential/images/geogebra_elektrisch_standbild6.png
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)

Damit ergibt sich für die Verschiebearbeit

W=q( φb - φa ) .

Im homogenen E → -Feld ist der Betrag der elektrischen Feldstärke konstant: | E → |=E= konstant. Die Arbeit für die Verschiebung gegen das Feld um die Strecke s beträgt

W=q·E·s .



Video 21: Arbeit, Energie und Potential im elektrischen Feld, Beispiel (C) .



Beispiel 5.1.37  
Welche Arbeit wird aufgewendet, um ein Elektron in einem elektrischen Feld mit einer Feldstärke von 1  V m einen Meter weit zu bewegen? Gegeben sei: q=e, s=1 m, E=1  V m .



 

Elektrische Spannung (!)


Video 22: Die elektrische Spannung (C) .



Die Potentialdifferenz ( φb - φa ) ist die elektrische Spannung U:

U=( φb - φa )=- ∫a b E ds= W q  .

Diese Definition der Spannung gilt nicht nur für Punktladungen, sondern ist allgemeingültig.

Die Einheit der Spannung ist: [U]= J C = 1 C ·N·m=:V ( Volt ).

Sie wurde benannt nach dem italienischen Physiker A. Volta (1745–1827), der als einer der ersten die elektrische Spannung beschrieb. Das Volt ist keine SI-Basiseinheit, sondern abgeleitet aus den Einheiten Joule und Coulomb.

Genau wie die mechanische Arbeit ist auch die elektrische Arbeit unabhängig vom genauen Verlauf des Weges. Die Arbeit hängt nur vom Anfangs- und Endpunkt ab.

Die potentielle Energie in der Elektrizitätslehre wird je nach Literatur auch als elektrische Energie E el bezeichnet. Begegnet einem der Begriff „potentielle Energie“ im Zusammenhang mit elektrischen Feldern, muss man genau hinsehen, welche Energieform wirklich gemeint ist: die elektrische Energie oder die mechanische potentielle Energie. Auch darf man die potentielle Energie nicht mit dem „elektrischen Potential“ verwechseln.

Beispiel 5.1.38  
Welche Geschwindigkeit v hat ein Elektron mit q=e, me =9,1· 10-31  kg dass durch eine Spannung von U=10 V aus der Ruhe beschleunigt wurde.





Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Verwenden Sie e=1,602 · 10-19   C und ε0 =8,854 · 10-12   A s V m  .










Details zum elektrischen Potential

Video 23: Das elektrische Potential: Erdung und Äquipotentialflächen (C) .



Die elektrische Spannung ist definiert als die Potentialdifferenz zwischen zwei Punkten P1 und P2 im Raum. Zur Erinnerung:

U=- ∫ P1 P2 E(s) ds=φ( P2 )-φ( P1 ) .



Messen kann man nur Spannungen, also Potentialunterschiede!


Das elektrische Potential ist nicht eindeutig festgelegt sondern kann um einen beliebigen konstanten Wert verschoben werden, d.h. die Wahl des Nullpotentials ist beliebig. Häufig wählt man den Bezugspunkt P1 so, dass φ( P1 )=0 gewählt werden kann. Ein solcher Bezugspunkt ist zum Beispiel die gesamte Erde, man spricht dann von „Erdpotential“ oder „erden“. Ein weiteres Beispiel hierfür wäre ein großer Körper aus Metall, der auch als „Masse“ bezeichnet wird. In beiden Fällen ist die Gesamtladung auf dem Körper so groß, dass durch das Hinzufügen oder Abfließen von Ladungen keine merkliche Änderung der Gesamtladung verursacht wird.

Ändert sich das Potential entlang eines Weges nicht, so gilt:

φ( P2 )=φ( P1 ) .

Dann ist die Spannung U=φ( P2 )-φ( P1 )=0. Damit ist auch die geleistete Arbeit W=q·U=0. Linien und Flächen, auf denen sich das Potential nicht ändert, heißen Äquipotentiallinien bzw. Äquipotentialflächen. Sie stehen immer senkrecht zu den elektrischen Feldlinien. Für eine Punktladung zum Beispiel sind die Äquipotentialflächen Kugelflächen.

In der animierten Skizze in Abschnitt 5.1.2 können Sie sich Äquipotentiallinien bei zwei Punktladungen ansehen.

Video 24: Arbeit entlang eines geschlossenen Weges im el. Feld (C) .



 

Arbeit entlang eines geschlossenen Weges im elektrischen Feld (*)


Anhand der Beziehung zwischen Potential und Spannung sieht man auch, dass die Arbeit, die auf einem in sich geschlossenen Weg im elektrischen Feld geleistet wird, immer null sein muss. Betrachten wir dazu zunächst den folgenden Weg im elektrischen Feld einer Punktladung:

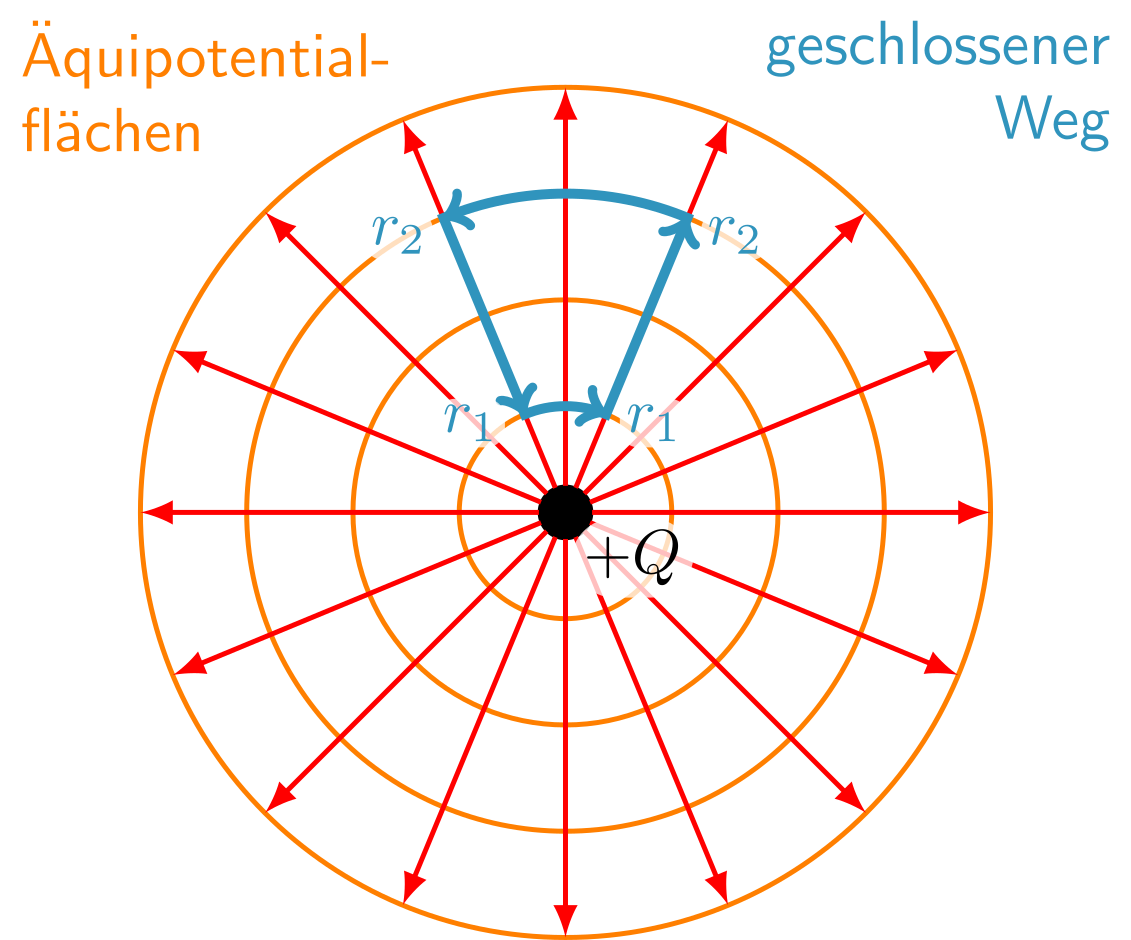
./_CFFDF8D1_4x.png
Abbildung 5.1.86: Geschlossener Weg im elektrischen Feld einer Punktladung  (C)



  • erstes Wegstück: antiparallel zu den Feldlinien von r2 nach r1 .
    Auf diesem Wegstück muss zur Überwindung der elektrischen Abstoßung Arbeit aufgewendet werden:

    W1 = ∫ r2 r1 q· Q 4π ε0 ( 1 s2 )ds=-q· Q 4π ε0 ( 1 r2 - 1 r1 ) .



  • zweites Wegstück: auf einer Äquipotentialfläche mit Radius r1 : Auf diesem Wegstück wird keine Arbeit verrichtet, W2 =0.

  • drittes Wegstück: parallel zu den Feldlinien von r1 nach r2 .
    Auf diesem Wegstück wird durch die abstoßende Kraft vom System Arbeit verrichtet, es wird Energie frei:

    W3 =-q· Q 4π ε0 ( 1 r1 - 1 r2 )=- W1  .



  • viertes Wegstück: auf einer Äquipotentialfläche mit Radius r2 zurück zum Ausgangspunkt: Auf diesem Wegstück wird keine Arbeit verrichtet, W4 =0.

Die gesamte entlang des geschlossenen Weges verrichtete Arbeit ist dann

W ges = W1 + W2 + W3 + W4 =0 .



Verallgemeinern wir diese Betrachtung jetzt und berechnen die Arbeit entlang eines beliebigen geschlossenen Weges S, der vom Punkt P → 1 zum Punkt P → 2 und wieder zurück führt.

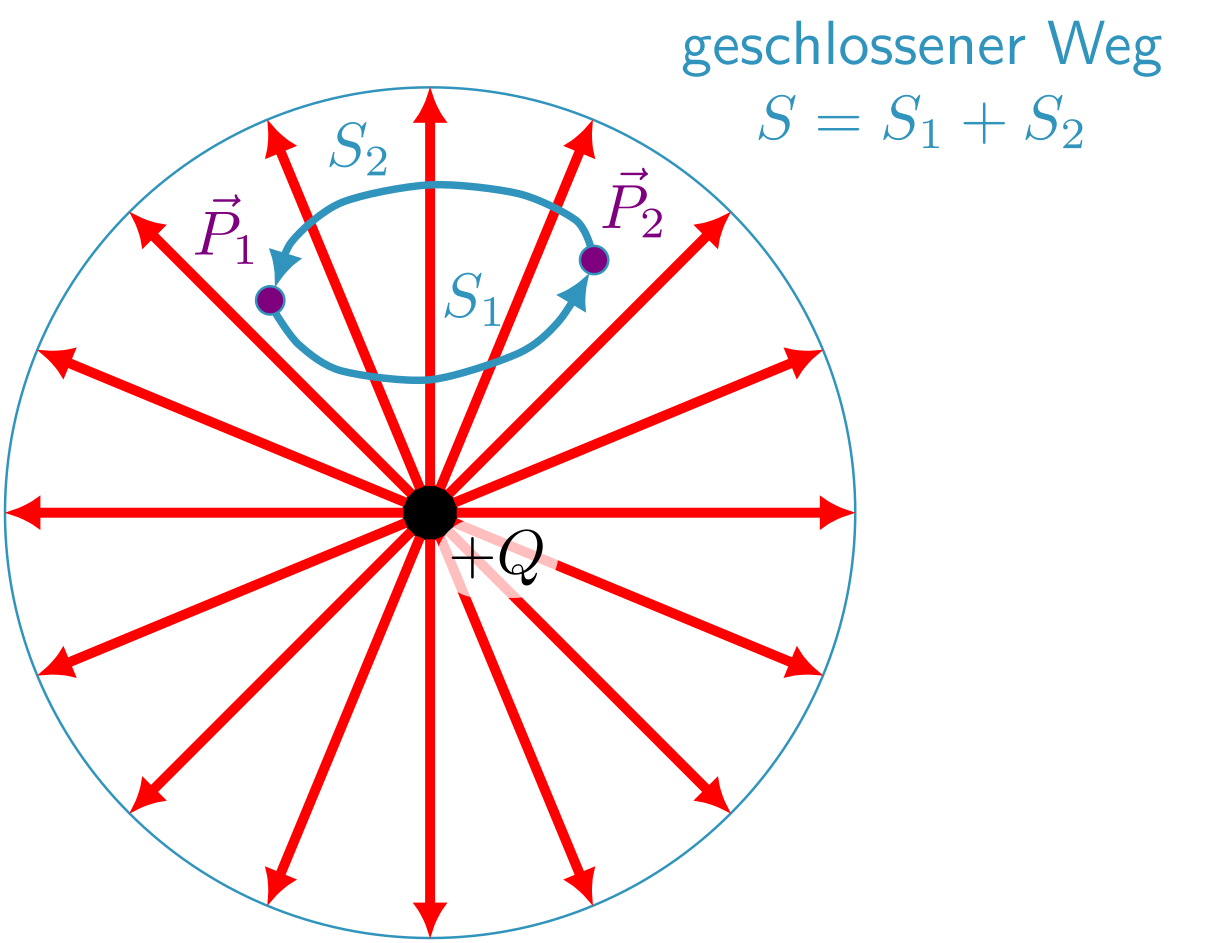
./_496334FC_4x.png
Abbildung 5.1.87: Geschlossener Weg im elektrischen Feld einer Punktladung  (C)



Wie wir gesehen haben, ist es egal, auf welcher Wegstrecke wir von P → 1 nach P → 2 gelangen. Wir können den geschlossenen Weg also aufteilen in zwei halbe Wegstrecken S1 von P → 1 nach P → 2 und S2 von P → 2 nach P → 1 .

Dann erhalten wir für die Arbeit:

W12 = -q ∫ P → 1 P → 2 E → ( s → )·d s → =q(φ( P → 2 )-φ( P → 1 )) , W21 = -q ∫ P → 2 P → 1 E → ( s → )·d s → =q(φ( P → 1 )-φ( P → 2 ))=- W12  , W ges = W12 + W21 =0 .

Das muss auch so sein, denn sonst könnte man durch das mehrfache Durchlaufen von geschlossenen Wegen in einem elektrischen Feld Energie erzeugen, was der Energieerhaltung widersprechen würde. Diese Beziehung gilt für jedes elektrische Feld, unabhängig von seiner genauen Form.



Video 25: Das Potential beliebiger Ladungsverteilungen (C) .



 

Das elektrische Potential beliebiger Ladungsverteilungen (*)


Das elektrische Potential, das durch eine beliebige Verteilung von Punktladungen an einem Ort erzeugt wird, kann einfach durch Addition der Potentiale der einzelnen Punktladungen berechnet werden. Man erhält für das Potential eine Funktion, die vom Ort abhängt. Punkte mit gleichem Potential bilden (zumeist gekrümmte) Flächen, die Äquipotentialflächen. Betrachtet man einen zweidimensionalen Schnitt, also z.B. die Verteilung des Potentials in der x- y-Ebene, so ergeben sich Äquipotentiallinien. Die Äquipotentiallinien stehen senkrecht auf den Feldlinien.

In der folgenden Simulation können Sie oben links zwei Punktladungen Q1 und Q2 in der x- y-Ebene verschieben. Außerdem kann jeweils die Größe der Ladungen eingestellt werden. Rechts wird das Potential der beiden Punktladungen dreidimensional dargestellt.

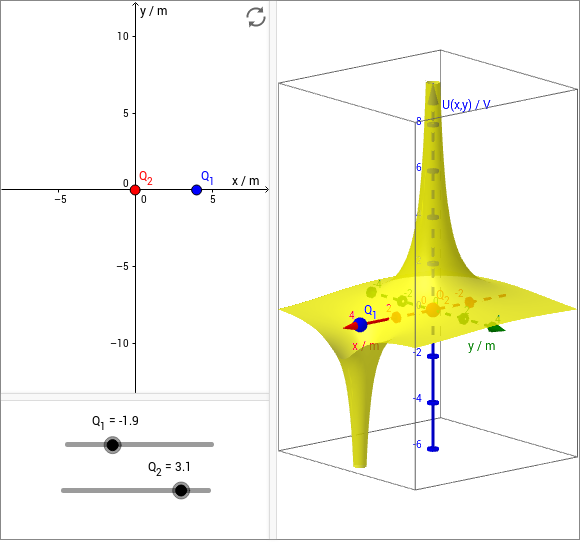
././Physikkurs/elektrisch_spannungpotential/images/geogebra_elektrisch_standbild7.png
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)

Wir wissen, dass für das Coulomb-Potential gilt:



φ(r)= Q 4π ε0 · 1 r

Man sieht hier aber, dass es ein Problem gibt, denn das Potential wird unendlich groß, wenn der Radius r gegen Null geht. Dies wird in der GeoGebra-Animation durch die Polstellen angedeutet. Dieses Problem löste erst die Quantenmechanik im 20. Jahrhundert, und wir können uns im Rahmen dieses Kurses nicht näher damit befassen. In der Praxis ist die Punktladung immer auf der Oberfläche einer kleinen Kugel mit einem endlichen Radius aufgebracht, sodass man eine Spannung zwischen der Oberfläche der Kugel und einer äußeren Elektrode angeben kann.