4.4.1 Impulserhaltung
Kraftstoß (+)
Video 1: Definition Kraftstoß (C)
.
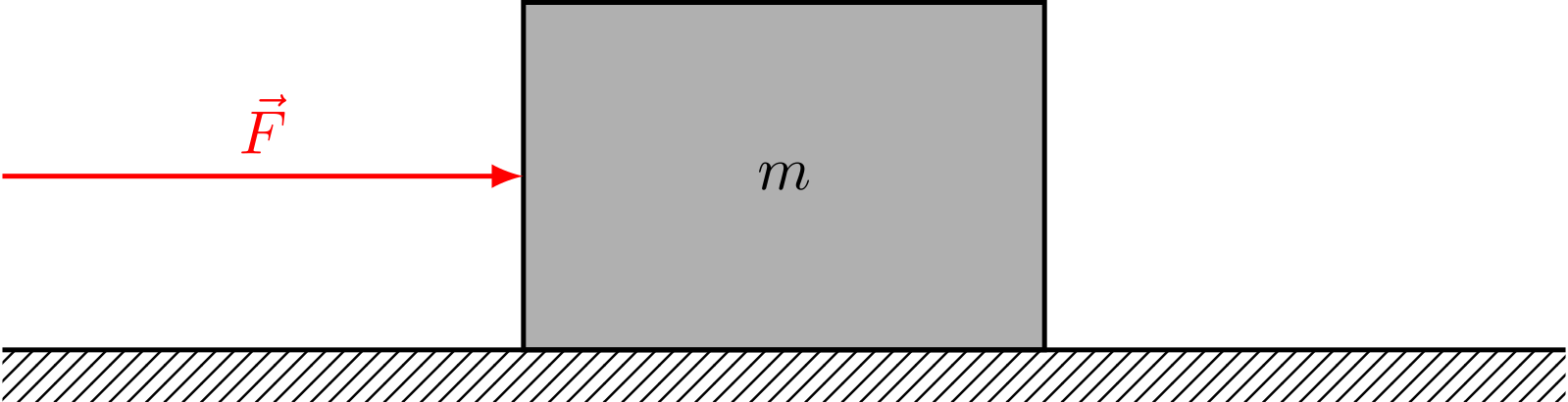
Abbildung 4.4.1: Kraft auf Körper (C)
Der Körper habe die Anfangsgeschwindigkeit . Dann erreicht er mit der konstanten Beschleunigung während einer Zeitdauer die Endgeschwindigkeit
Ist die Beschleunigung nicht konstant, ergibt sich
Video 2: Beispiel zum Kraftstoß (C)
.
Beispiel
4.4.1
Ein Körper wird über einen Zeitraum von mit einer konstanten Kraft reibungsfrei angeschoben. Berechnen Sie den von der Kraft bewirkten Kraftstoß.

Ein Körper wird über einen Zeitraum von mit einer konstanten Kraft reibungsfrei angeschoben. Berechnen Sie den von der Kraft bewirkten Kraftstoß.

Abbildung 4.4.2: Kraftstoß auf Körper (C)
Video 3: Beispiel zum Kraftstoß (C)
.
Beispiel
4.4.2
Ein ruhender Körper der Masse wird mit einer konstanten Kraft über eine Strecke von reibungsfrei angeschoben, bevor er frei gleiten kann.
Berechnen Sie den durch die Kraft bewirkten Kraftstoß.
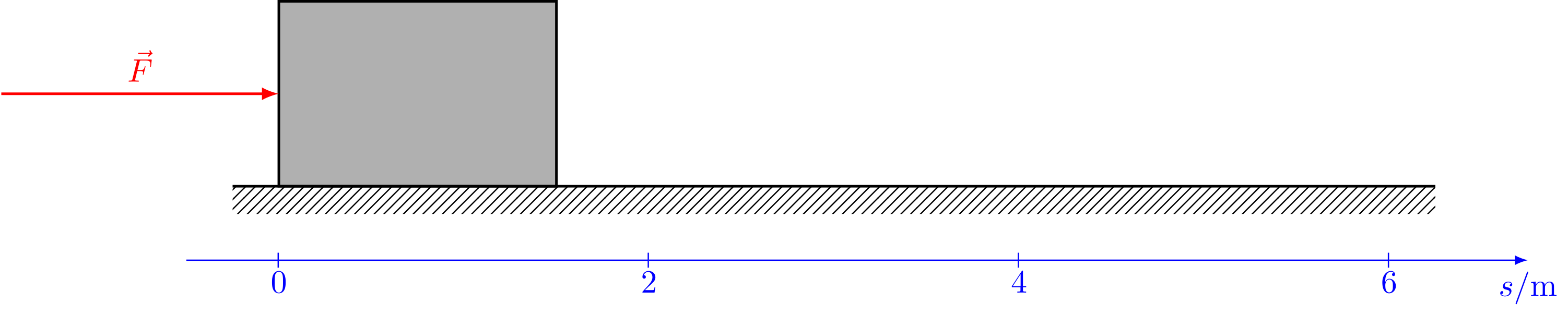
Ein ruhender Körper der Masse wird mit einer konstanten Kraft über eine Strecke von reibungsfrei angeschoben, bevor er frei gleiten kann.
Berechnen Sie den durch die Kraft bewirkten Kraftstoß.

Abbildung 4.4.3: Körper wird auf einer Strecke mit konstanter Kraft angeschoben (C)
Video 4: Beispiel zum Kraftstoß (C)
.
Beispiel
4.4.3
Auf einen quaderförmigen Körper, der über einen reibungsfreien Untergrund gleitet, wirkt eine Kraft mit
über einen Zeitraum von . Berechnen Sie den Kraftstoß, der durch die Kraft bewirkt wird.

Auf einen quaderförmigen Körper, der über einen reibungsfreien Untergrund gleitet, wirkt eine Kraft mit
über einen Zeitraum von . Berechnen Sie den Kraftstoß, der durch die Kraft bewirkt wird.

Abbildung 4.4.4: Kraftstoß auf Körper (C)
Impuls (!)
Video 5: Definition Impuls (C)
.
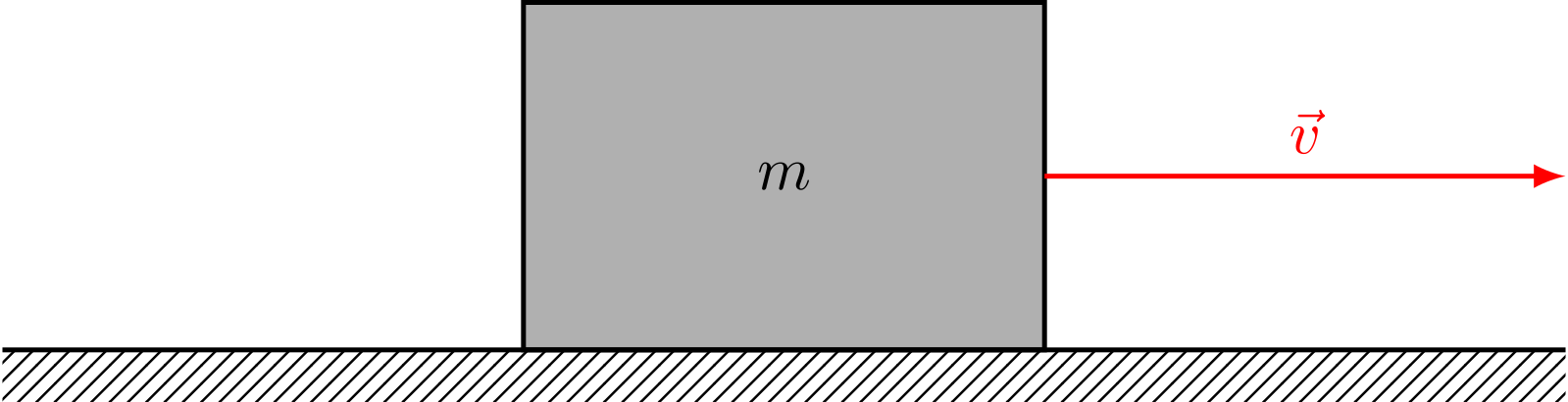
Abbildung 4.4.5: Körper mit Geschwindigkeit (C)
Die Einheit des Impulses ist
Leitet man den Impuls nach der Zeit ab, geht dabei von einer konstanten Masse aus und nutzt schließlich das zweite newtonsche Axiom, ergibt sich:
Die Integration dieser Gleichung liefert
Ein Kraftstoß, der auf einen Körper einwirkt, führt also unmittelbar zu einer Impulsänderung des Körpers.
Aus dieser Gleichung folgt auch, dass Kraftstoß und Impuls die gleiche physikalische Einheit besitzen.
Video 6: Beispiel Impuls und Kraftstoß (C)
.
Beispiel
4.4.4
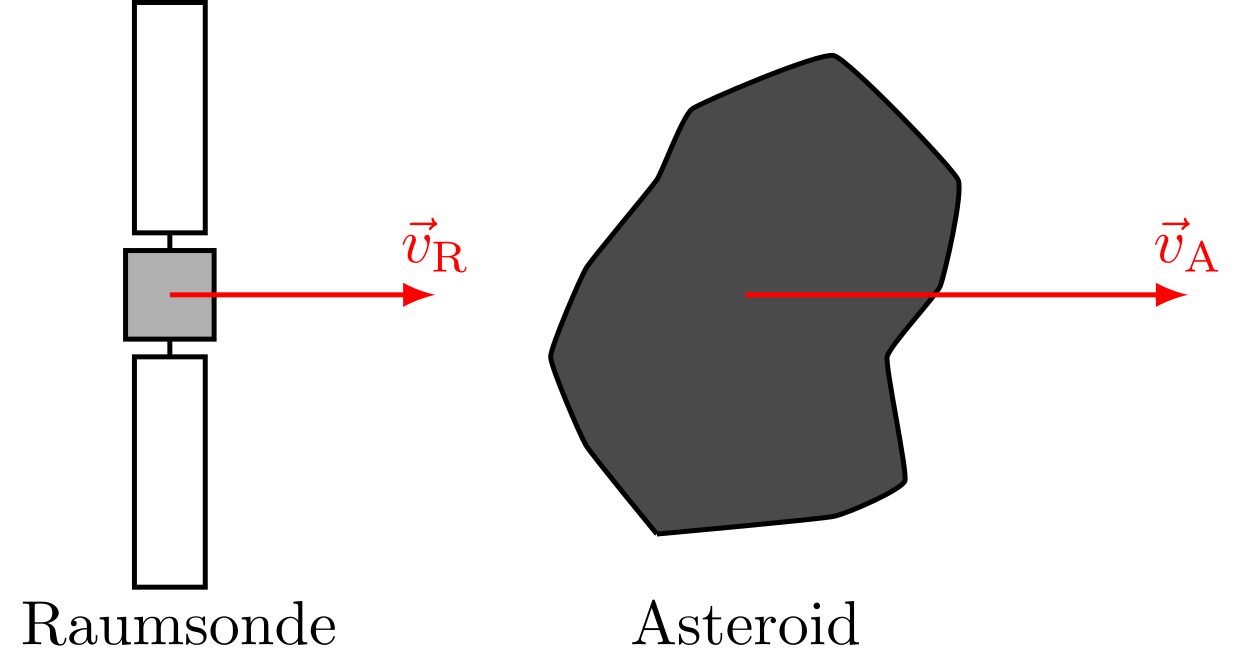
Eine Raumsonde der Masse bewegt sich mit der Geschwindigkeit geradlinig durch den Weltraum. Ein Asteroid der Masse bewegt sich mit der Geschwindigkeit entlang derselben Geraden.

Abbildung 4.4.6: Raumsonde und Asteroid (C)
Eine Raumsonde der Masse bewegt sich mit der Geschwindigkeit geradlinig durch den Weltraum. Ein Asteroid der Masse bewegt sich mit der Geschwindigkeit entlang derselben Geraden.
- Berechnen Sie die Impulse und von
Raumsonde und Asteroid.
-
Um auf dem Asteroiden landen zu können, muss die Raumsonde abgebremst werden.
Berechnen Sie den dazu nötigen Kraftstoß.
Bewegungsgesetz (!)
Video 7: Impuls und zweites newtonsches Axiom (C)
.
Das zweite newtonsche Axiom kann nun auch mit Hilfe des Impulses ausgedrückt werden:
Auch hier wurde wieder von einer konstanten Masse ausgegangen.
Das zweite newtonsche Axiom gilt jedoch auch allgemeiner für veränderliche Massen:
Ein bekanntes Beispiel, bei dem sich die Masse während des Beschleunigungsvorgangs ändert, ist die Rakete. Diese verliert durch den Ausstoß der Treibgase ständig an Masse. Ein anderes Beispiel sind Elementarteilchen in einem Beschleuniger. Hier werden diese oft bis in die Nähe der Lichtgeschwindigkeit beschleunigt und erfahren dabei eine Massenzunahme entsprechend der Vorhersage der Relativitätstheorie. In solchen Fällen kann man die neue Formulierung der Bewegungsgleichung anwenden. Da nun neben der Geschwindigkeit auch die Masse als Funktion der Zeit betrachtet wird, muss für die Ableitung des Impulses nach der Zeit die Produktregel angewendet werden:
Als Ergebnis erhält man eine Differentialgleichung. Dies ist eine Gleichung, in der sowohl die betrachtete Variable als auch ihre Ableitung vorkommen. Mit Hilfe von weiterführenden mathematischen Methoden kann man sie lösen und so die Bewegung berechnen.
Impulserhaltung (!)
Video 8: Impulserhaltung (C)
.
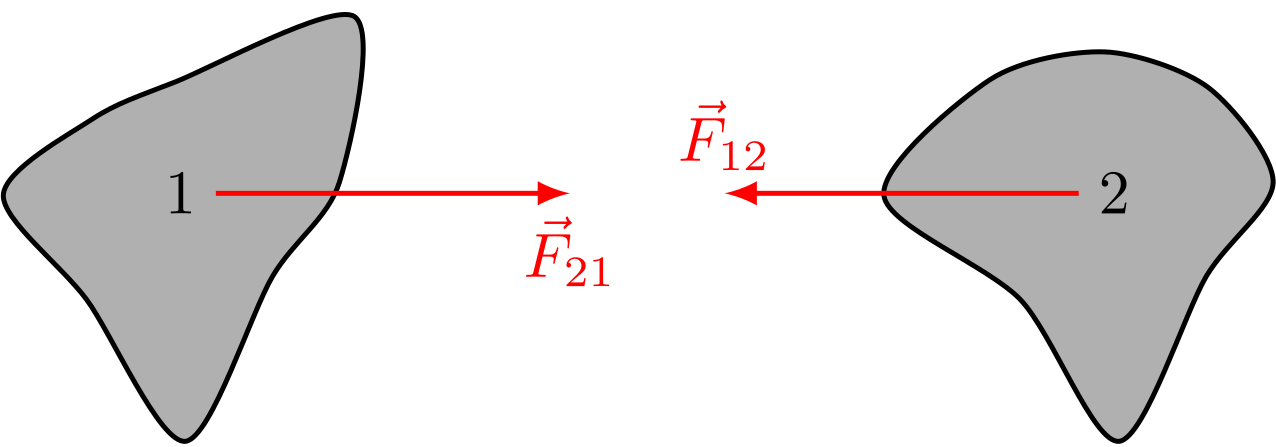
Abbildung 4.4.7: Abgeschlossenes System (C)
Dies sind die einzigen Kräfte, die auf die beiden Körper wirken. Daher gilt:
Video 9: Beispiel zur Impulserhaltung (C)
.
Beispiel
4.4.5
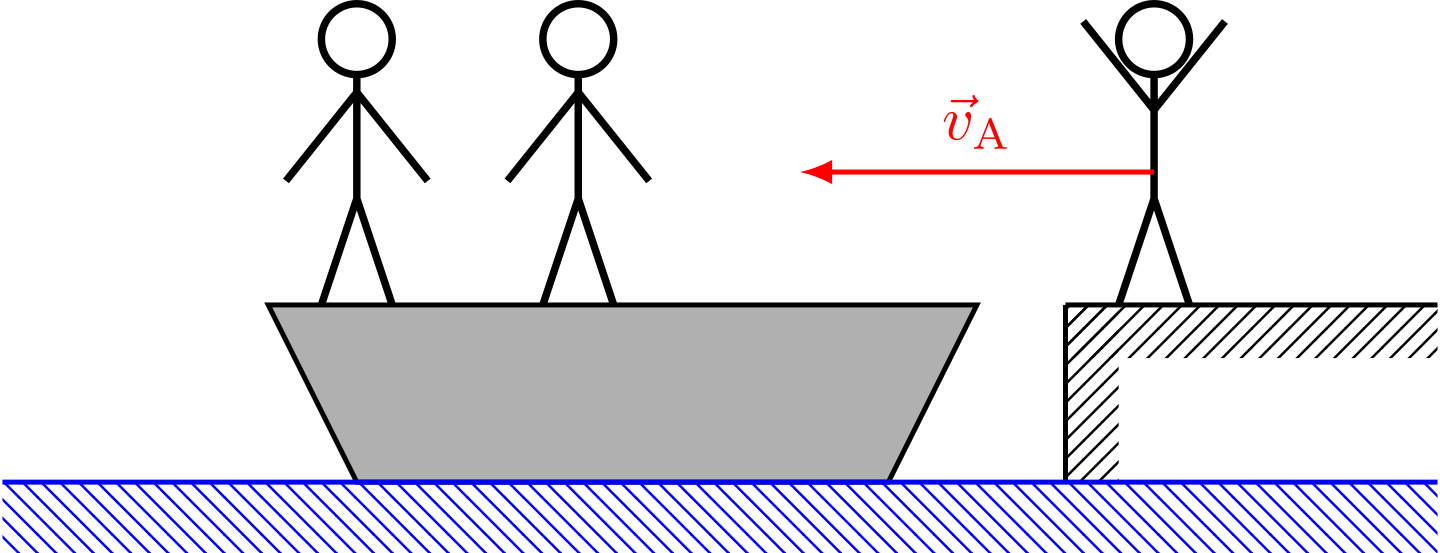
Zwei Personen (jeweils der Masse ) stehen in einem ruhenden Boot der Masse . Eine dritte Person der Masse springt mit einer horizontalen Geschwindigkeit auf das Boot.
Berechnen Sie die Geschwindigkeit , mit der sich das Boot nach der Landung der dritten Person bewegt.

Abbildung 4.4.8: Person springt auf Boot (C)
Zwei Personen (jeweils der Masse ) stehen in einem ruhenden Boot der Masse . Eine dritte Person der Masse springt mit einer horizontalen Geschwindigkeit auf das Boot.
Berechnen Sie die Geschwindigkeit , mit der sich das Boot nach der Landung der dritten Person bewegt.
Video 10: Beispiel zur Impulserhaltung (C)
.
Beispiel
4.4.6

Drei Personen (jeweils der Masse ) stehen in einem ruhenden Boot der Masse . Eine der Personen springt mit einer horizontalen Geschwindigkeit vom Boot ins Wasser.
Berechnen Sie die Geschwindigkeit , mit der sich das Boot nach dem Absprung bewegt.

Abbildung 4.4.9: Person springt auf Boot auf (C)
Drei Personen (jeweils der Masse ) stehen in einem ruhenden Boot der Masse . Eine der Personen springt mit einer horizontalen Geschwindigkeit vom Boot ins Wasser.
Berechnen Sie die Geschwindigkeit , mit der sich das Boot nach dem Absprung bewegt.
Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie .
Falls nicht anders angegeben, verwenden Sie

