8.1.3 Verschiedene Wellenarten
Eindimensionale Festkörperwellen
Video 3: Wellen in Festkörpern und Wasserwellen (C)
.
Video 4: Schallwellen (C)
.
Video 5: Elektromagnetische Wellen (C)
.
In einem langen dünnen Stab können sich Wellen transversal oder longitudinal ausbreiten. Sein Durchmesser muss deutlich kleiner als die Wellenlänge der durchlaufenden Welle sein, damit die Querkontraktion vernachlässigt werden kann.
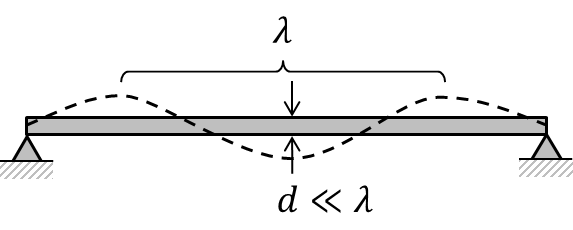
Analog gilt für die Ausbreitungsgeschwindigkeit in einem gespannten Seil:
Oberflächenwellen in Wasser
Die Form und Ausbreitungsgeschwindigkeit von Oberflächenwellen in Wasser hängen im Wesentlichen von der Art der Anregung, der Wellenlänge und der Wassertiefe ab. Die Wellenbewegung ist eine Kombination aus Transversal- und Longitudinalbewegung. Zwei wichtige Wellentypen entstehen unter dem Einfluss der Schwerkraft (Schwerewellen):
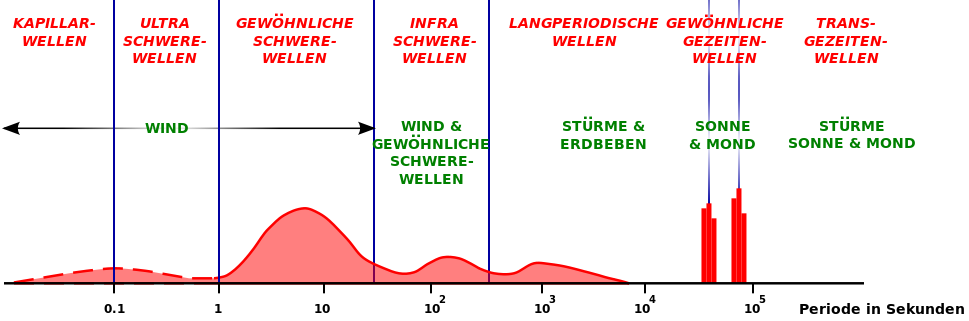
Relative Amplitude von Wasserwellen
Ebene Schallwellen (+)
Im physikalischen Sinn bedeuten Schallwellen die Ausbreitung von kleinen Druck- bzw. Dichteschwankungen in einem deformierbaren (kompressiblen) Medium. Es handelt sich um longitudinale Wellen, da die Auslenkung der Partikel in Ausbreitungsrichtung erfolgt. Als Medium kommen Gase, Flüssigkeiten und Festkörper in Frage, die je nach Beschaffenheit eine unterschiedliche Schallgeschwindigkeit besitzen.
Ausbreitung einer ebenen Schallwelle in einer Luftsäule
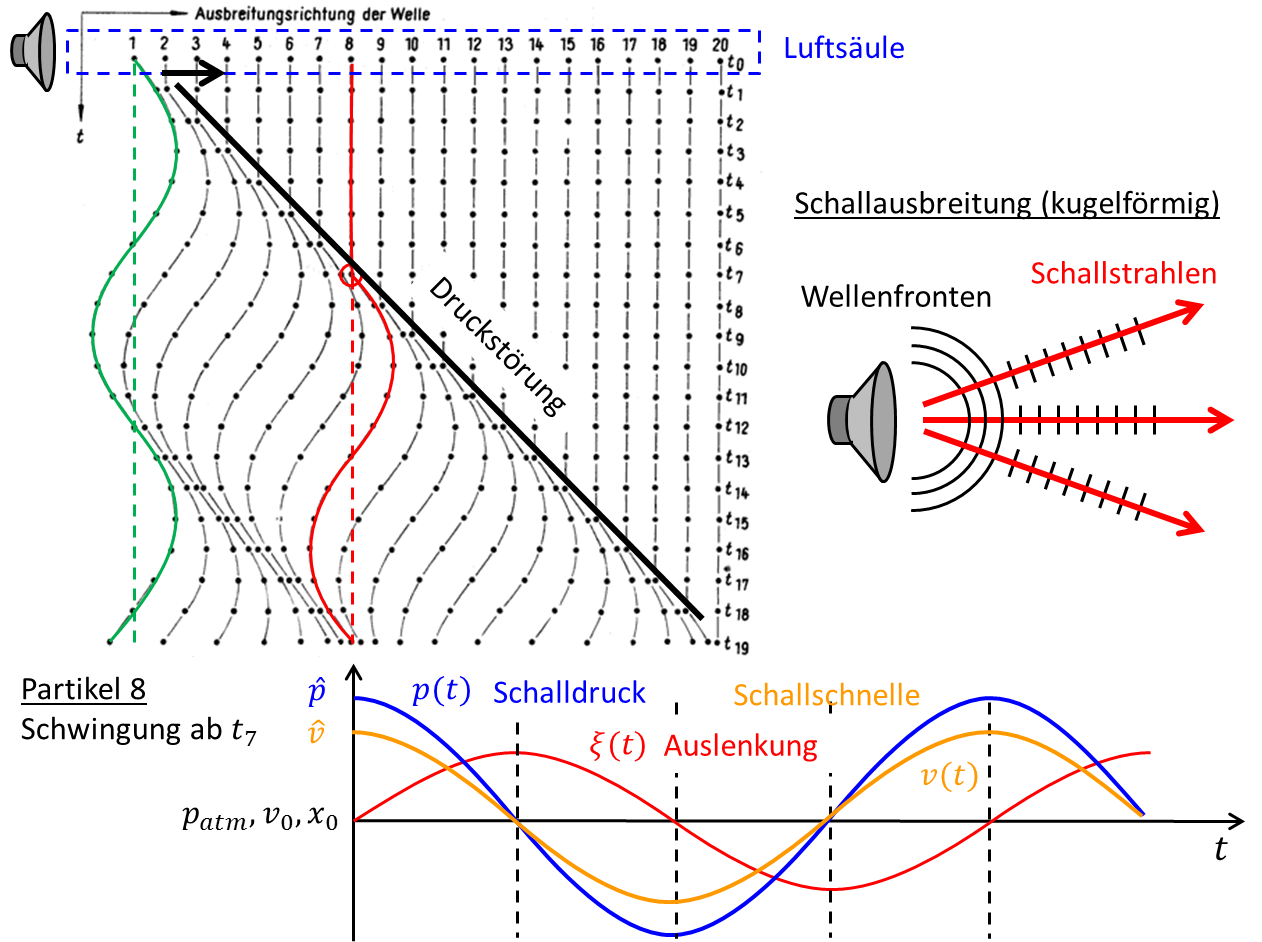
Bei einer punktförmigen Schallquelle breitet sich der Schall eigentlich kugelförmig aus. In der geometrischen Akustik stellt man sich vor, dass die Quelle in alle Richtungen 1-dim. Schallstrahlen aussendet. Die Wechselgrößen an einer festen Position (s.u.) sind dabei den Umgebungsgrößen überlagert ( Windgeschwindigkeit, atmosphärischer Druck):
Der Schalldruck ist die wichtigste Schallgröße, da er gut wahrnehmbar (mittels Trommelfell im menschlichen Ohr) und messbar (Mikrofon) ist. Da sich die Werte des Schalldruckes je nach Schallquelle um viele Größenordnungen unterscheiden können, ist die Verwendung einer logarithmischen Skala bzw. das Einführen eines Schalldruckpegels sinnvoll:
Hinweis
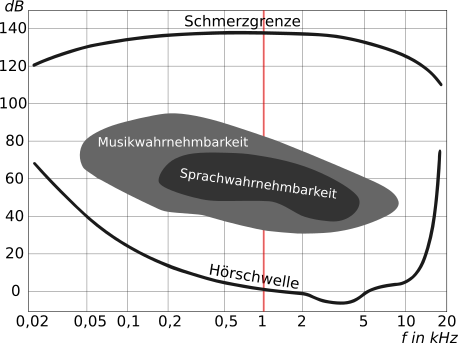
Der Hörbereich bezeichnet den Frequenz- und Pegelbereich, den ein Mensch wahrnehmen kann. Der Bereich ist nach unten durch die Hörschwelle und nach oben durch die Schmerzgrenze beschränkt. Sowohl Hörschwelle als auch Schmerzgrenze sind frequanzabhänig. Die folgende Abbildung zeigt beispielhaft den Hörbereich des Menschen.
Elektromagnetische Wellen (+)
Eine elektromagnetische Welle besteht aus sich gegenseitig induzierenden elektrischen und magnetischen Feldern. Beide Felder ändern sich gleichphasig und die Feldvektoren stehen aufeinander senkrecht. Elektromagnetische Strahlung setzt sich aus vielen elektromagn. und transversalen Wellen zusammen, deren Feldvektoren in der Regel in alle Richtungen statistisch verteilt sind (unpolarisierte Strahlung). Sie entstehen z.B. bei der Beschleunigung von freien elektrischen Ladungen.
Mögliche Quellen von im Alltag relevanter Strahlung können sein:
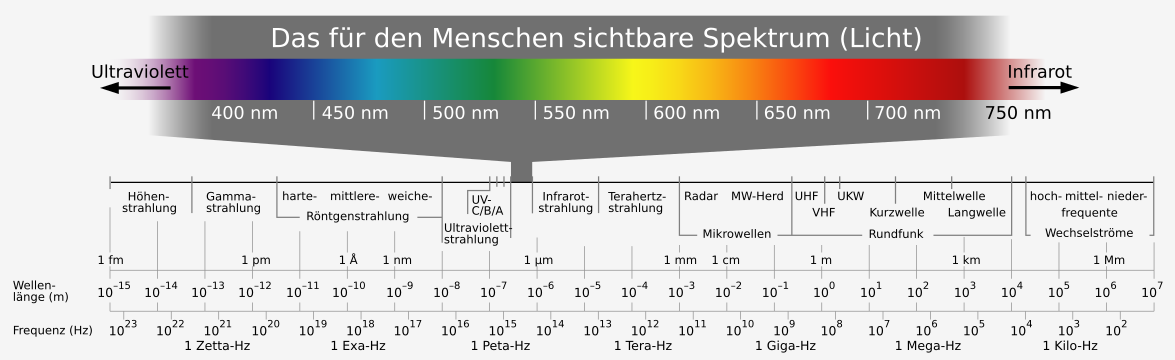
Spektrum der elektromagnetischen Strahlung
Entstehung einer elektromagnetischen Welle im Hertz’schen Dipol
Durch die periodische Auf-und-ab-Bewegung von Elektronen in einem Leiter (Dipol) werden direkt am Dipol (Nahfeld) ein elektrisches () und ein um phasenverschobenes magnetisches Feld () erzeugt. Die Feldvektoren stehen immer aufeinander senkrecht. Sobald sich die elektrischen Felder ablösen und geschlossene Feldlinien bilden (Fernfeld), breitet sich eine elektromagnetische Welle in beide Richtungen aus, deren Felder jetzt phasengleich schwingen:
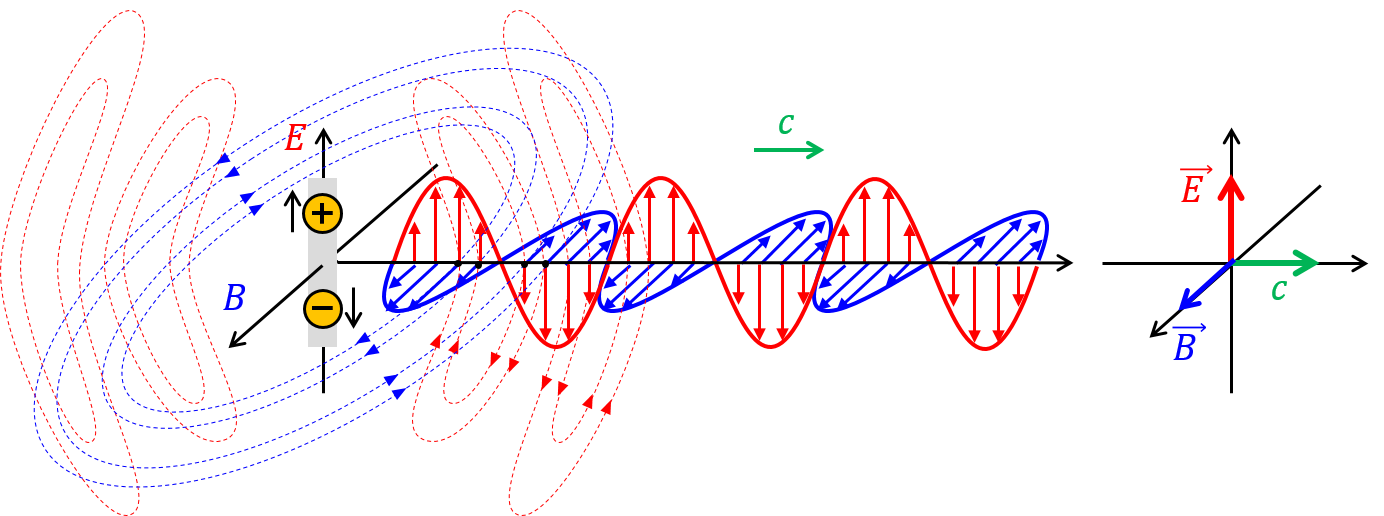

Abbildung 8.1.155: Welle in langem dünnem Stab (C)
Welleneigenschaften (longitudinal und transversal)
Wellenfunktion
Die Ausbreitungsgeschwindigkeit von Wellen in Festkörpern (hier: langer dünner Stab) hängt von den elastischen Materialeigenschaften und der Dichte ab.
Langer dünner Stab:
Wellenleistung:
Wellenfunktion
Die Ausbreitungsgeschwindigkeit von Wellen in Festkörpern (hier: langer dünner Stab) hängt von den elastischen Materialeigenschaften und der Dichte ab.
Langer dünner Stab:
| mit | Schubmodul | |
| Materialdichte |
| mit | Elastizitätsmodul |
Gespanntes Seil / Saite:
Wellenleistung:
| mit | Spannkraft | |
| Massendichte (Masse pro Länge) |
Oberflächenwellen in Wasser
Die Form und Ausbreitungsgeschwindigkeit von Oberflächenwellen in Wasser hängen im Wesentlichen von der Art der Anregung, der Wellenlänge und der Wassertiefe ab. Die Wellenbewegung ist eine Kombination aus Transversal- und Longitudinalbewegung. Zwei wichtige Wellentypen entstehen unter dem Einfluss der Schwerkraft (Schwerewellen):
| Tiefwasserwellen | |
| Die Wellenform ähnelt einer Trochoide (bzw. Zykloide, Abrollkurve eines Punktes auf einer rotierenden Scheibe).
Die Wasserteilchen führen eine kreisförmige Bewegung aus | 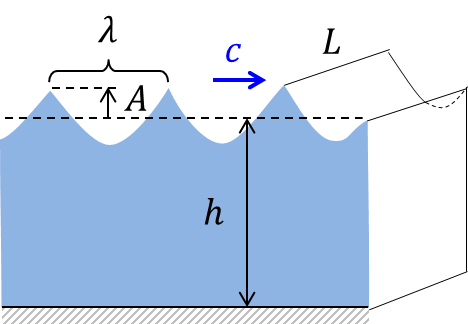 (C)
(C)
|
| Flachwasserwellen | |
| Die Wellenform kann durch eine Sinusform angenähert werden.
Die Wasserteilchen führen eine ellipsenförmige Bewegung aus (bei extrem flachem Wasser fast nur horizontal) | 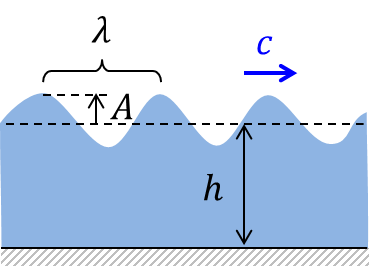 (C)
(C)
|
Welleneigenschaften
Wellenfunktion (Flachwasserwelle)
Ausbreitungsgeschwindigkeit
Wellenfunktion (Flachwasserwelle)
Ausbreitungsgeschwindigkeit
| Tiefwasser | () | |
| Flachwasser | () | |
| Wellenleistung | (nur Tiefwasserwellen) |
| mit | Wassertiefe | ||
| Erdbeschleunigung | |||
| Wellenlänge | |||
| Wasserdichte | |||

Abbildung 8.1.158: Relative Amplitude von Wasserwellen (C)
Beispiel
8.1.15
Ein Wellenkraftwerk soll längs eines langen Küstenstreifens aufgebaut werden. Die Wassertiefe ist , die Wellenhöhe und die Wellenlänge .
Ein Wellenkraftwerk soll längs eines langen Küstenstreifens aufgebaut werden. Die Wassertiefe ist , die Wellenhöhe und die Wellenlänge .
| a) | Welcher Wellentyp liegt vor? |
| b) | Wie groß ist die Ausbreitungsgeschwindigkeit der Wellen? |
| c) | Welche maximale Leistung kann das Kraftwerk haben? |
Ebene Schallwellen (+)
Im physikalischen Sinn bedeuten Schallwellen die Ausbreitung von kleinen Druck- bzw. Dichteschwankungen in einem deformierbaren (kompressiblen) Medium. Es handelt sich um longitudinale Wellen, da die Auslenkung der Partikel in Ausbreitungsrichtung erfolgt. Als Medium kommen Gase, Flüssigkeiten und Festkörper in Frage, die je nach Beschaffenheit eine unterschiedliche Schallgeschwindigkeit besitzen.
Ausbreitung einer ebenen Schallwelle in einer Luftsäule

Abbildung 8.1.159: Ausbreitung einer ebenen Schallwelle in einer Luftsäule (C)
Bei einer punktförmigen Schallquelle breitet sich der Schall eigentlich kugelförmig aus. In der geometrischen Akustik stellt man sich vor, dass die Quelle in alle Richtungen 1-dim. Schallstrahlen aussendet. Die Wechselgrößen an einer festen Position (s.u.) sind dabei den Umgebungsgrößen überlagert ( Windgeschwindigkeit, atmosphärischer Druck):
Physikalische Größen im Schallfeld
| Wechselgrößen: | Absolute Größen: | ||
| Auslenkung | () | Position | |
| Schallschnelle | () | Geschwindigkeit | |
| Schalldruck | () | Druck |
Wellenleistung (bei ebenen fortschreitenden Wellen)
Schallleistung
Schallleistung
| mit | vom Schall durchflossene Fläche |
Definition
| Schalldruckpegel | ||
| Bezugsschalldruck | (Hörschwelle) |
- Der Bezugsschalldruck beschreibt die Hörschwelle bei der Frequenz . Das menschliche Ohr kann Schall im Bereich von bis wahrnehmen.
- Die Basis 10 wurde gewählt, da so ein Unterschied von im Schalldruckpegel von zwei Schallereignissen gerade noch hörbar ist.

Abbildung 8.1.160: Hörbereich des Menschen. Rot markiert ., der Frequenz des Bezugsschalldrucks. (C)
Beispiel
8.1.16
Berechnen Sie die Schallschnelle und Partikelauslenkung für den gegebenen Schalldruck. Gegeben: Schalldruck eines Presslufthammers:
Berechnen Sie die Schallschnelle und Partikelauslenkung für den gegebenen Schalldruck. Gegeben: Schalldruck eines Presslufthammers:
Beispiel
8.1.17
| a) | Ein Disko-Lautsprecher erzeugt den Schalldruck . Wie groß ist der entsprechende Schalldruckpegel? |
| b) | LKW 1 erzeugt einen Schalldruck, der doppelt so groß ist wie der von LKW 2. Wie groß ist der Unterschied der Schalldruckpegel? |
| c) | Der durchschnittliche Schalldruckpegel an einer Hauptstraße ist . Bestimmen Sie den entsprechenden Schalldruck. |
| d) | Der Schalldruckpegel eines Lautsprechers wird um reduziert. Wie groß ist das Verhältnis der Schalldrücke zwischen den beiden Zuständen? |
Elektromagnetische Wellen (+)
Eine elektromagnetische Welle besteht aus sich gegenseitig induzierenden elektrischen und magnetischen Feldern. Beide Felder ändern sich gleichphasig und die Feldvektoren stehen aufeinander senkrecht. Elektromagnetische Strahlung setzt sich aus vielen elektromagn. und transversalen Wellen zusammen, deren Feldvektoren in der Regel in alle Richtungen statistisch verteilt sind (unpolarisierte Strahlung). Sie entstehen z.B. bei der Beschleunigung von freien elektrischen Ladungen.
Mögliche Quellen von im Alltag relevanter Strahlung können sein:
| Wellentyp | Entstehung durch |
| Radio- bzw. Funkwellen | Oszillation makroskopischer Ströme in Antennen (z.B. Hertz’scher Dipol) |
| Licht | Sprünge von elektrischen Ladungen in versch. Energieniveaus innerhalb eines Atoms |
| Röntgenstrahlung | Abbremsen von Elektronen beim Eintritt in ein Metall |
| Thermische Strahlung | Thermisch angeregte Bewegung von Ladungen innerhalb eines Moleküls |
Welleneigenschaften
| Wellenfunktion | ||
| Ausbreitungsrichtung | Kreuzprodukt | |
| Zusammenhang der Feldstärken | Wellenwiderstand (s.u.) | |
| Lichtgeschwindigkeit (im Vakuum) | ||
| Strahlungsleistung | (eines Strahlers mit der Oberfläche ) |
| mit | Elektrische Feldstärke | ||
| Magnetische Flussdichte | |||
| Magn. Feldkonstante | () | ||
| Elektr. Feldkonstante | () |

Abbildung 8.1.161: Spektrum der elektromagnetischen Strahlung (C)
Entstehung einer elektromagnetischen Welle im Hertz’schen Dipol
Durch die periodische Auf-und-ab-Bewegung von Elektronen in einem Leiter (Dipol) werden direkt am Dipol (Nahfeld) ein elektrisches () und ein um phasenverschobenes magnetisches Feld () erzeugt. Die Feldvektoren stehen immer aufeinander senkrecht. Sobald sich die elektrischen Felder ablösen und geschlossene Feldlinien bilden (Fernfeld), breitet sich eine elektromagnetische Welle in beide Richtungen aus, deren Felder jetzt phasengleich schwingen:

Abbildung 8.1.162: Entstehung einer elektromagnetischen Welle im Hertz’schen Dipol (C)

