5.1.2 Elektrisches Feld
Basiswissen – Elektrisches Feld
Eine Ladung verändert den sie umgebenden Raum. Sie kann über eine Distanz eine Kraft auf einen zweiten geladenen Körper ausüben. Das ist nicht einfach zu verstehen. Faraday entwickelte zur besseren Vorstellung das Modell des Feldes. Dabei wechselwirkt ein Körper über eine Distanz mit anderen Körpern, ohne direkten Kontakt zu haben. Ein beobachtbares Beispiel für ein Feld und seine Wirkung ist das Gravitationsfeld der Erde. Ein Apfel fällt auf den Boden, ohne in direktem Kontakt mit der Erde zu sein.
Das Konzept Feld wird auf elektrische Ladungen übertragen. Jede Ladung ist von einem elektrischen Feld umgeben. Dieses Feld durchdringt den gesamten Raum. Über das elektrische Feld wechselwirkt die Ladung mit anderen Ladungen.
Um ein Feld darzustellen, werden die sogenannten Feldlinien eingeführt. Per Definition ist die Richtung der elektrischen Feldlinien von Plus nach Minus. In der Abbildung ist links das Feld um eine negative Punktladung gezeigt. Das Feld ist mit Feldlinien dargestellt. Die Feldlinien enden auf ihrer Oberfläche. Rechts ist eine positive Punktladung zu sehen. Die Feldlinien beginnen auf ihrer Oberfläche. Die Richtung der Feldlinien und des Feldes ist in den Skizzen durch Pfeile gekennzeichnet:
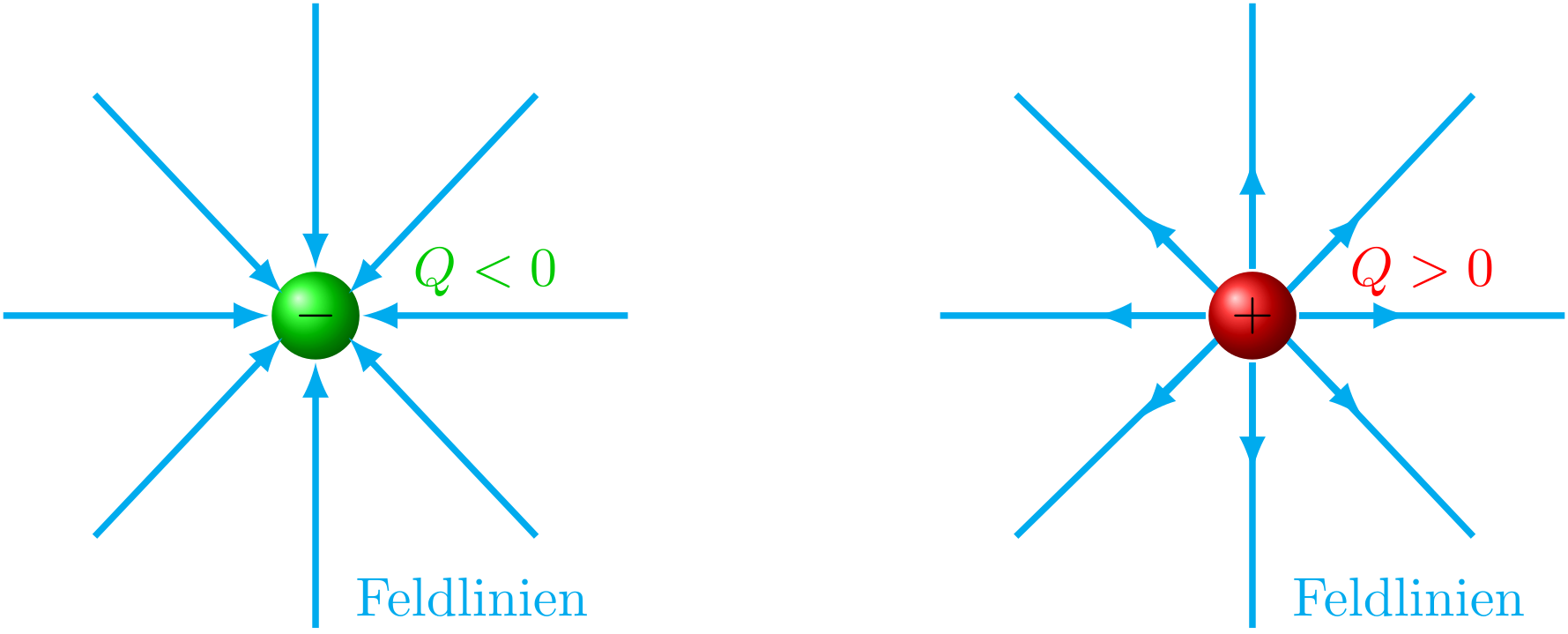
Abbildung 5.1.50: Feld einer negativen (links) und einer positiven Punktladung mit Feldlinien (C)
Zwischen positiven und negativen Ladungen existiert ein elektrisches Feld. Feldlinien eines elektrischen Feldes:
- beginnen auf dem positiv geladenen Körper.
- enden auf dem negativ geladenen Körper.
Wird in das Feld der Ladung eine Probeladung gebracht, wechselwirkt über das sie umgebende Feld mit der Probeladung . Für eine punktförmige negative Ladung ist dies exemplarisch in der Abbildung gezeigt. Dabei kennzeichnet eine Feldlinie den Weg, auf dem sich eine Probeladung der Ladung nähert, beziehungsweise den Weg, auf dem sich eine Ladung von entfernt. Positive Ladungen bewegen sich in Richtung der Feldlinien, negative Ladungen bewegen sich gegen die Richtung Feldlinien. Die Richtung der Feldlinien gibt die Richtung des elektrischen Feldes an.
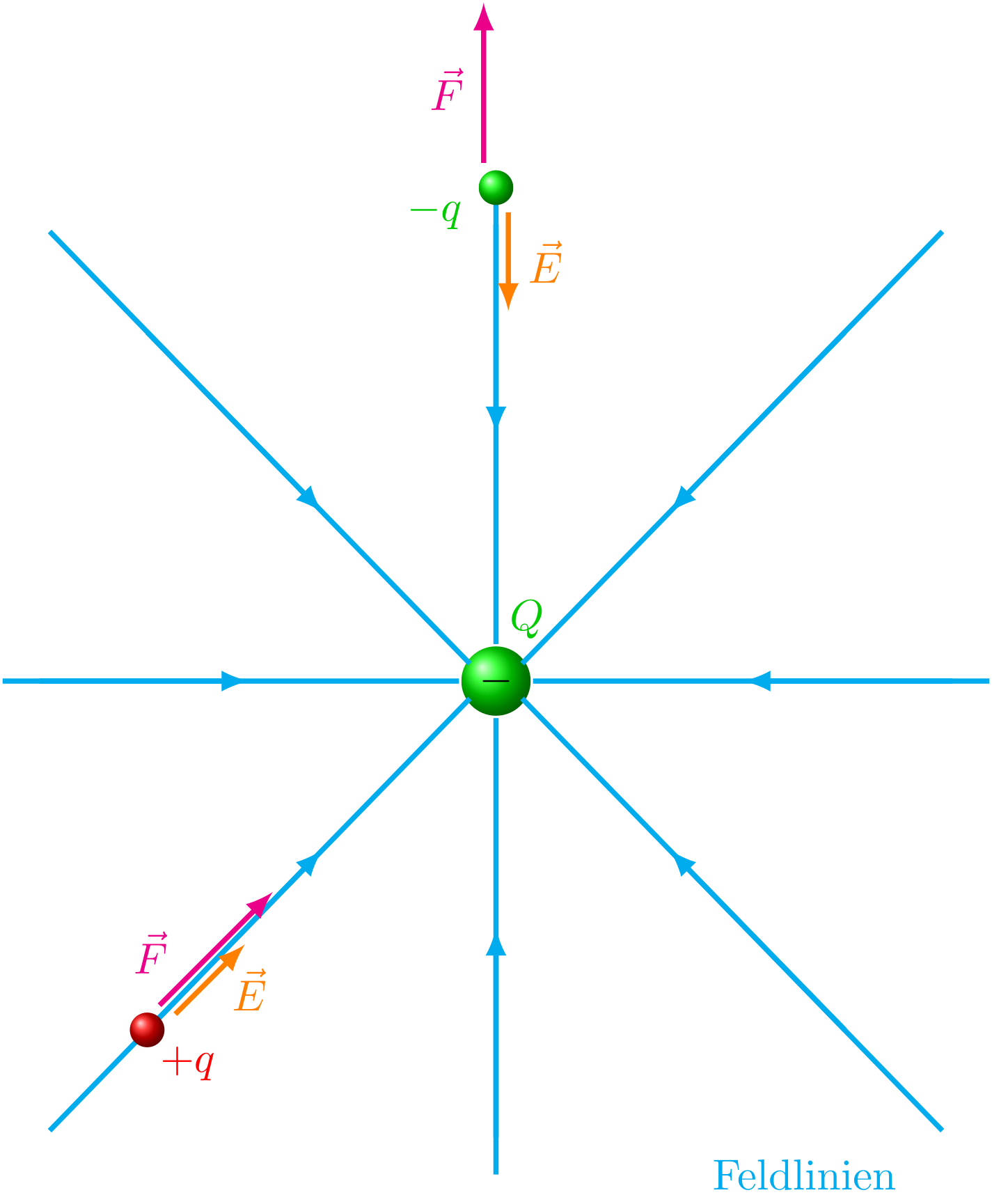
Abbildung 5.1.51: Elektrische Kraft auf eine negative () und eine positive () Punktladung im Feld einer negativen Ladung (C)
- Materie besitzt Eigenschaften, die in ihrer Umgebung messbar sind. Auf Proben werden durch diese Eigenschaften Kräfte ausgeübt, ohne dass direkter Kontakt besteht.
- Mit dem Feld ist die Beschreibung der auf die Probe wirkenden elektrischen Kraft möglich.
- Die Feldstärke ist ein Vektor in Richtung der Feldlinien. Für die Kraft auf eine Probeladung gilt:
- Die Einheit der elektrischen Feldstärke ist .
Beispiel
5.1.16
Welche Kraft erfährt eine Punktladung in einem Feld von ?
Es gilt:
Welche Kraft erfährt eine Punktladung in einem Feld von ?
Es gilt:
Basiswissen – Koordinatensysteme, Einheitsvektoren und Vektorfelder
Jeder Punkt im dreidimensionalen Raum kann mit Hilfe von Koordinatensystemen beschrieben werden. Bei vielen Problemen hat sich bewährt, sogenannte orthogonale Koordinatensysteme zu verwenden. Diese Koordinatensysteme sind dadurch ausgezeichnet, dass die Koordinatenachsen , und , die sich im Ursprung treffen und den Raum aufspannen, senkrecht zueinander stehen. Jeder beliebige Vektor kann als Addition von zueinander senkrechten Vektoren , und dargestellt werden.
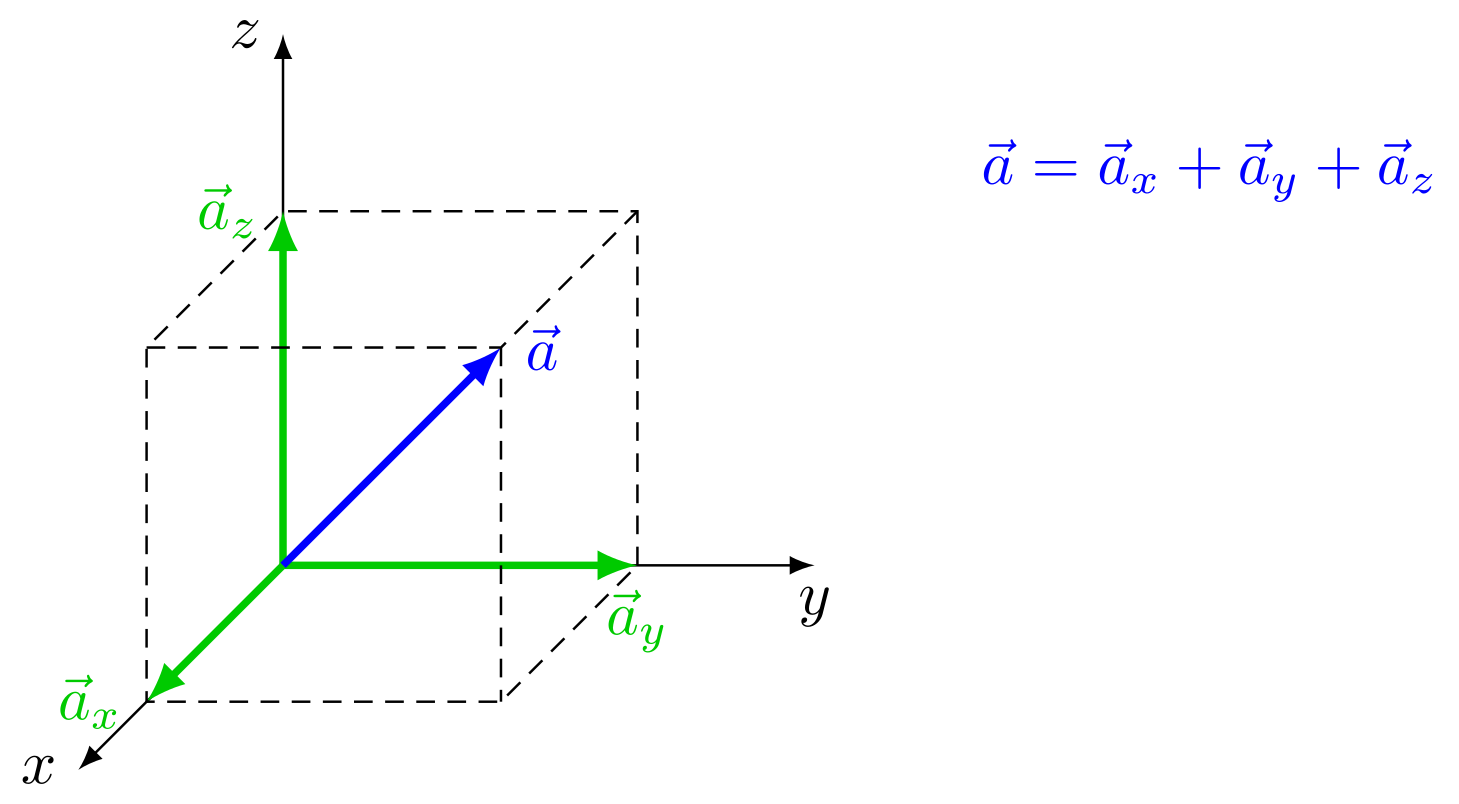
Abbildung 5.1.52: Vektor in kartesischem Koordinatensystem (C)
Die Einführung von sogenannten Einheitsvektoren, die die Richtungen des Koordinatensystems angeben, erleichtert oftmals die Arbeit. Ein Einheitsvektor ist ein Vektor, der auf die Länge normiert ist. Die Einheitsvektoren , und zeigen in Richtung , und . Werden diese Einheitsvektoren zur Darstellung des obigen Vektors verwendet, ergibt sich mit den Koordinaten , und :
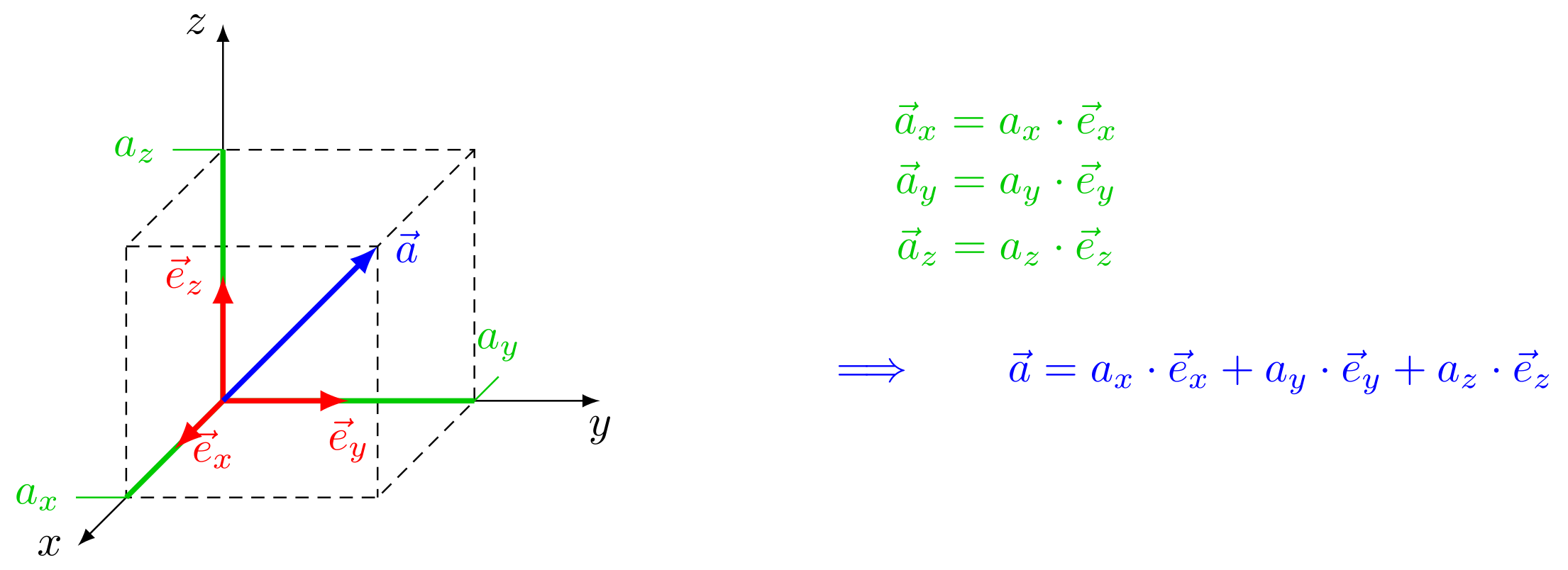
Die Einheitvektoren , und spannen den Raum auf und besitzen die Länge . Sie bilden eine orthonormale Basis des Raums. Jeder beliebige Punkt im Raum kann durch diese Basisvektoren beschrieben werden.
Damit ergibt sich für den normierten Vektor
Beispiel
5.1.17
Der Vektor soll auf die Länge normiert werden:
Dazu wird zuerst der Betrag des Vektors berechnet:
Der normierte Vektor ergibt sich also zu:
Er zeigt in die gleiche Richtung wie , hat aber lediglich die Länge .
Der Vektor soll auf die Länge normiert werden:
Dazu wird zuerst der Betrag des Vektors berechnet:
Der normierte Vektor ergibt sich also zu:
Er zeigt in die gleiche Richtung wie , hat aber lediglich die Länge .
Die Lage eines Punktes und damit auch des zugehörigen Ortsvektors kann auch mit sogenannten Kugelkoordinaten angegeben werden. Dazu werden der Abstand des Punktes vom Ursprung und zwei Winkel und verwendet. Der Abstand des Punktes entspricht ja gerade dem Betrag des Ortsvektors . Der Winkel findet sich zwischen der positiven -Achse und der Projektion des Vektors auf die --Ebene. Der Winkel wird von der positiven -Achse und dem Vektor eingeschlossen. Das ist in der nachfolgenden Abbildung veranschaulicht.
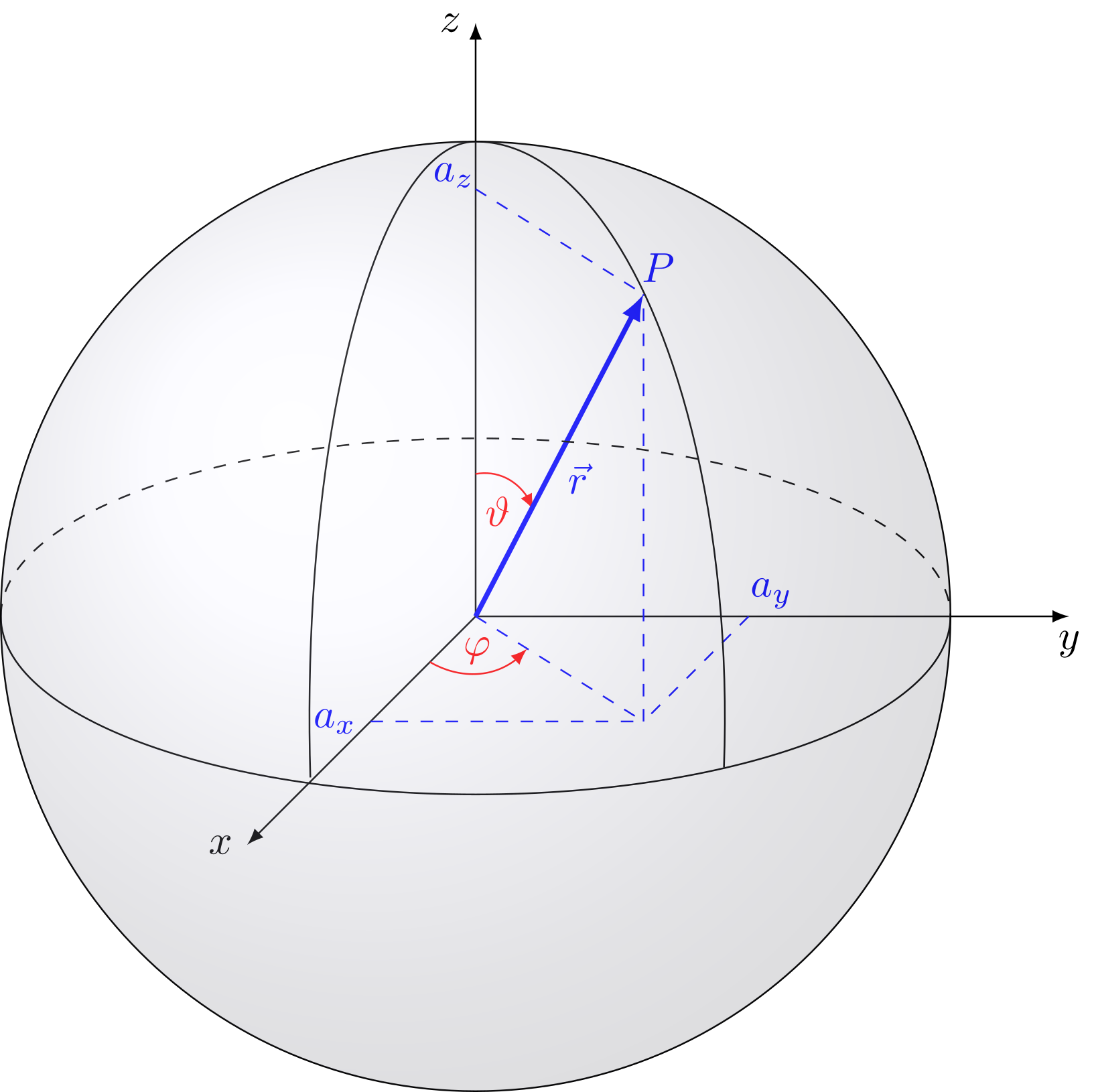
Abbildung 5.1.54: Ortsvektor mit den Winkeln und (C)
Geometrische Überlegungen führen zum Zusammenhang zwischen kartesischen Koordinaten und Kugelkoordinaten:
Kugelkoordinaten werden vor allem zur Bearbeitung von kugelsymmetrischen Problemen verwendet. Eine elektrische Punktladung besitzt z.B. ein kugelsymmetrisches Vektorfeld. Unter einem Vektorfeld versteht man eine Funktion, die jedem Raumpunkt einen Vektor zuordnet. Dies soll im Folgenden veranschaulicht werden.
Beispiel
5.1.18
Es soll das Feld einer Ladung an verschiedenen Punkten im Raum betrachtet werden. Zur Vereinfachung wird das Koordinatensystem so gewählt, dass sich die Punktladung im Ursprung des gewählten Koordinatensystems befindet. Für das elektrische Feld gilt:
Mit dieser Formel kann das Feld an jedem beliebigen Punkt im Raum berechnet werden. In der Tabelle wurde für einen Abstand allgemein das Feld ausgerechnet. Die Feldstärke wurde auch für den doppelten und dreifachen Abstand berechnet. Mit zunehmender Entfernung nimmt die Feldstärke ab. In der graphischen Darstellung eines Vektorfeldes wird die Feldstärke durch Pfeile dargestellt. Je größer die Feldstärke, desto länger der Pfeil.
Da in die Formel nur der Abstand eingeht, ergibt sich in einem konstanten Abstand immer derselbe Wert für die Feldstärke, egal wo sich der Punkt befindet. Zeichnet man einen Kreis mit Radius um die Ladung, so beträgt die Feldstärke auf diesem Kreis immer . Auf einem Kreis mit doppeltem Abstand ist die Feldstärke auf ein Viertel des Wertes gesunken.
Da das Feld kugelsymmetrisch ist, kann auch die Richtung des Feldes angegeben werden. Abhängig von der Ladungsart ist das Feld entweder zur Ladung hin oder von ihr weg gerichtet. Im dargestellten Fall zeigt das Feld zur negativen Ladung hin.
In der Skizze wird die Feldstärke entlang der Kreise mit Pfeilen dargestellt, deren Länge der Feldstärke entspricht. Bei größerem Radius werden entsprechend kleinere Pfeile gezeichnet.
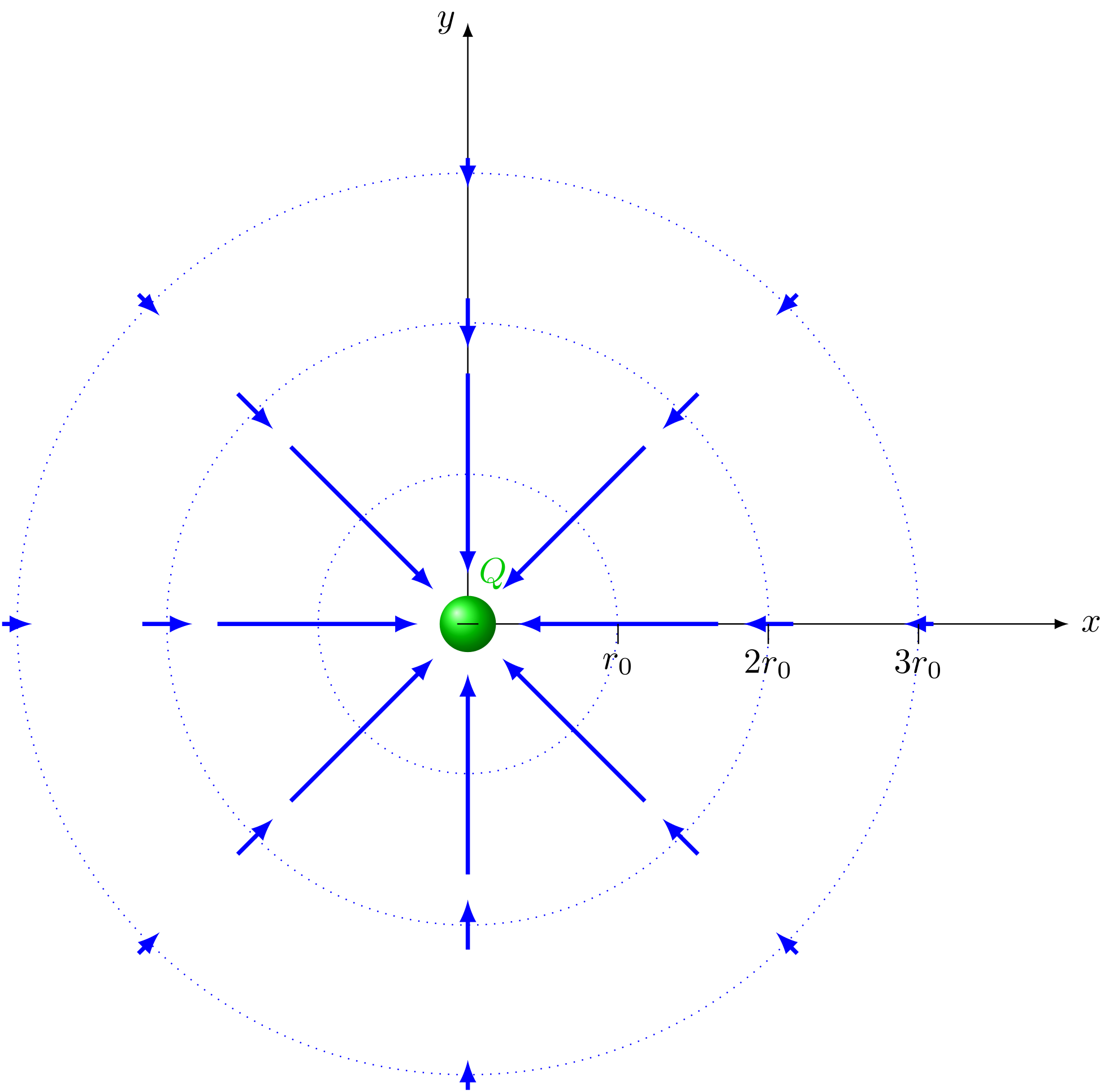
Das Beispiel veranschaulicht, dass das elektrische Feld ein Vektorfeld ist und was darunter zu verstehen ist. Jedem Raumpunkt wird ein Vektor, in diesem Fall die Feldstärke an dem Ort, zugeordnet.
Es soll das Feld einer Ladung an verschiedenen Punkten im Raum betrachtet werden. Zur Vereinfachung wird das Koordinatensystem so gewählt, dass sich die Punktladung im Ursprung des gewählten Koordinatensystems befindet. Für das elektrische Feld gilt:
Mit dieser Formel kann das Feld an jedem beliebigen Punkt im Raum berechnet werden. In der Tabelle wurde für einen Abstand allgemein das Feld ausgerechnet. Die Feldstärke wurde auch für den doppelten und dreifachen Abstand berechnet. Mit zunehmender Entfernung nimmt die Feldstärke ab. In der graphischen Darstellung eines Vektorfeldes wird die Feldstärke durch Pfeile dargestellt. Je größer die Feldstärke, desto länger der Pfeil.
| Abstand | Feldstärke | Darstellung |

| ||

| ||

|
Da in die Formel nur der Abstand eingeht, ergibt sich in einem konstanten Abstand immer derselbe Wert für die Feldstärke, egal wo sich der Punkt befindet. Zeichnet man einen Kreis mit Radius um die Ladung, so beträgt die Feldstärke auf diesem Kreis immer . Auf einem Kreis mit doppeltem Abstand ist die Feldstärke auf ein Viertel des Wertes gesunken.
Da das Feld kugelsymmetrisch ist, kann auch die Richtung des Feldes angegeben werden. Abhängig von der Ladungsart ist das Feld entweder zur Ladung hin oder von ihr weg gerichtet. Im dargestellten Fall zeigt das Feld zur negativen Ladung hin.
In der Skizze wird die Feldstärke entlang der Kreise mit Pfeilen dargestellt, deren Länge der Feldstärke entspricht. Bei größerem Radius werden entsprechend kleinere Pfeile gezeichnet.

Abbildung 5.1.58: Elektrisches Feld um eine Punktladung. Die Länge der Vektoren skaliert mit der Feldstärke (C)
Das Beispiel veranschaulicht, dass das elektrische Feld ein Vektorfeld ist und was darunter zu verstehen ist. Jedem Raumpunkt wird ein Vektor, in diesem Fall die Feldstärke an dem Ort, zugeordnet.
Aufgabe 5.1.19
Ein Teilchen mit einer Ladung von fliegt durch ein elektrisches Feld und erfährt dabei eine Kraft von . Ein zweites Teilchen mit einer Ladung von erfährt in einem anderen elektrischen Feld eine Kraft von . Wie groß sind die Feldstärken der beiden Felder?
E
E
Ein Teilchen mit einer Ladung von fliegt durch ein elektrisches Feld und erfährt dabei eine Kraft von . Ein zweites Teilchen mit einer Ladung von erfährt in einem anderen elektrischen Feld eine Kraft von . Wie groß sind die Feldstärken der beiden Felder?
E
E
Aufgabe 5.1.20
Bestimmen Sie das elektrische Feld einer punktförmigen Ladung im Abstand von .
E
In welche Richtung zeigt das Feld ?
Das Feld
Wie verändert sich das Feld , wenn der Abstand verdoppelt wird?
Bestimmen Sie das elektrische Feld einer punktförmigen Ladung im Abstand von .
E
In welche Richtung zeigt das Feld ?
Das Feld
Wie verändert sich das Feld , wenn der Abstand verdoppelt wird?
Aufgabe 5.1.21
Eine punktförmige elektrische Ladung der Masse befindet sich in einem elektrischen Feld . Was passiert mit der Ladung?
Wie groß ist die Kraft und die Beschleunigung auf das Teilchen?
E

Eine punktförmige elektrische Ladung der Masse befindet sich in einem elektrischen Feld . Was passiert mit der Ladung?
| Es wirkt eine Kraft auf das geladene Teilchen. | |
| Das Feld hat keinen Einfluss auf das geladene Teilchen. | |
| Das geladene Teilchen bewegt sich mit einer konstanten Geschwindigkeit durch das Feld. | |
| Das geladene Teilchen wird beschleunigt. |
Wie groß ist die Kraft und die Beschleunigung auf das Teilchen?
E
Aufgabe 5.1.22
Berechnen Sie den Abstand des Punktes vom Ursprung.

Berechnen Sie den Abstand des Punktes vom Ursprung.
Aufgabe 5.1.23
Normieren Sie den Vektor
Normieren Sie den Vektor
Elektrisches Feld und elektrische Feldstärke (!)
Video 6: Das elektrische Feld (C)
.
Bei der Gravitationskraft auf der Erdoberfläche ist es zweckmäßig, diese als zu schreiben. Die Masse erfährt also im Gravitationsfeld an der Erdoberfläche die Kraft .
Aus der Perspektive einer „Probeladung“ kann es ebenso zweckmäßig sein, die auf sie durch andere Ladungen ausgeübte Coulomb-Kraft als zu schreiben. Die Größe wird als elektrisches Feld bezeichnet. Vorsicht: Auch die Energie wird häufig mit bezeichnet, hier ist je nach Zusammenhang zu unterscheiden.
Hinweis: Tragen mehrere Ladungen zur Kraft auf die Probeladung bei ergibt sich eine resultierende Kraft und somit auch ein resultierendes Feld, siehe dazu Überlagerung elektrischer Felder: Superposition.
Elektrisches Feld
Eine elektrische Ladung oder Ladungsverteilung erzeugt in dem sie umgebenden Raum ein elektrisches Feld . Vektoriell ergibt sich aus der Kraft auf die Probeladung am Ort :
Eine elektrische Ladung oder Ladungsverteilung erzeugt in dem sie umgebenden Raum ein elektrisches Feld . Vektoriell ergibt sich aus der Kraft auf die Probeladung am Ort :
Die Einheit der elektrischen Feldstärke ist
Video 7: Beispiele für die Berechnung der elektrischen Feldstärke (C)
.
Die elektrische Feldstärke soll nun konkret für eine Punktladung bestimmt werden. In diesem Fall ist das elektrische Feld inhomogen, also ortsabhängig. Es wird angenommen, dass sich im Ursprung des Koordinatensystems befindet. ist ein Maß dafür, wie groß die elektrische Kraft der Punktladung auf eine Probeladung am Ort ist.
Elektrisches Feld einer Punktladung
Hierbei ist der Einheitsvektor, der vom Ort der Punktladung (hier: Ursprung) nach außen zeigt. Je nach Ladungsvorzeichen von und wird die Probeladung von der Punktladung abgestoßen oder von ihr angezogen. Elektrische Felder, die durch ruhende Ladungen erzeugt werden, nennt man elektrostatische Felder.
Hierbei ist der Einheitsvektor, der vom Ort der Punktladung (hier: Ursprung) nach außen zeigt. Je nach Ladungsvorzeichen von und wird die Probeladung von der Punktladung abgestoßen oder von ihr angezogen. Elektrische Felder, die durch ruhende Ladungen erzeugt werden, nennt man elektrostatische Felder.
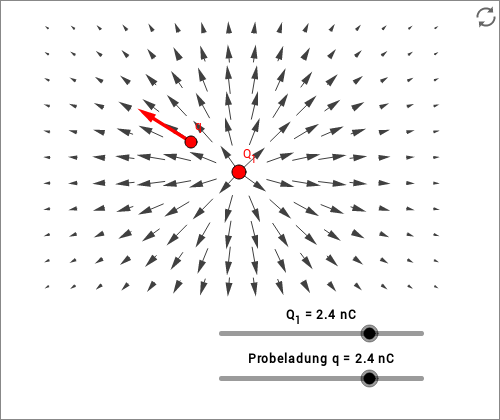
Das elektrische Feld einer Punktladung ist in der unten stehenden animierten Skizze veranschaulicht. An Punkten, die auf einem regelmäßigen Gitter der --Ebene angeordnet sind, werden Betrag und Richtung des elektrischen Felds als Vektorpfeile visualisiert. Die Probeladung können Sie durch dieses elektrische Feld bewegen. Die aus dem elektrischen Feld resultierende Kraft auf die Probeladung wird ebenfalls durch einen Vektorpfeil veranschaulicht. Die starke Zunahme der Kraft proportional zu bei Annäherung an die Punktquelle ist sehr deutlich zu sehen.
Video 8: Überlagerung elektrischer Felder: entgegengesetzte Ladungen (C)
.
Video 9: Überlagerung elektrischer Felder: gleichartige Ladungen (C)
.
Überlagerung elektrischer Felder: Superposition
Betrachtet man mehrere Punktladungen, so überlagern sich die elektrischen Felder der Einzelladungen. Zur Bestimmung der resultierenden elektrischen Feldstärke verwendet man das Superpositionsprinzip. Dies bedeutet, dass sich an jedem Punkt das elektrische Feld durch vektorielle Addition der Felder der Einzelladungen ergibt:
Betrachtet man mehrere Punktladungen, so überlagern sich die elektrischen Felder der Einzelladungen. Zur Bestimmung der resultierenden elektrischen Feldstärke verwendet man das Superpositionsprinzip. Dies bedeutet, dass sich an jedem Punkt das elektrische Feld durch vektorielle Addition der Felder der Einzelladungen ergibt:
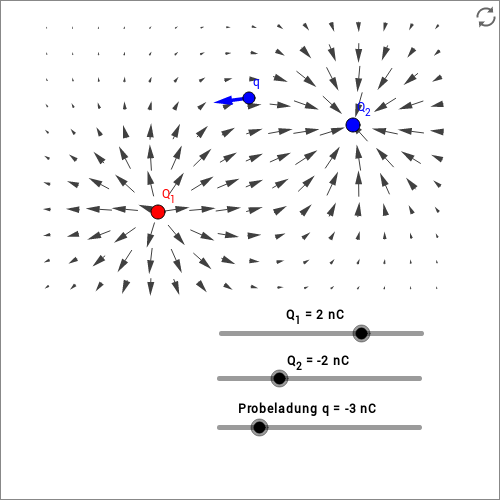
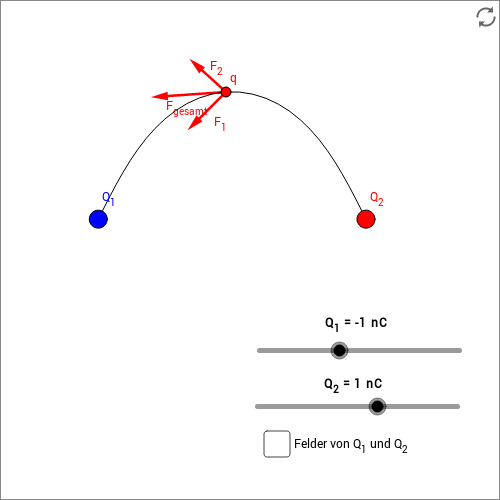
Dies ist in der folgenden animierten Skizze für den Fall von zwei Einzelladungen illustriert. Die Größen der beiden Einzelladungen können eingestellt werden. Eine Probeladung kann bewegt werden. Am Ort der Probeladung ist die vektorielle Addition der von und erzeugten elektrischen Felder dargestellt. Die Richtung des resultierenden elektrischen Feldes gibt auch die Richtung einer sogenannten Feldlinie vor, die durch die Probeladung läuft. Näheres zu den Feldlinien folgt weiter unten. Das durch die Vektoraddition berechnete Feld am Ort der Probeladung verläuft immer tangential zu den Feldlinien des Gesamtfeldes.
Feldvektoren (!)
Die elektrische Feldstärke an einem Punkt kann mit Hilfe eines sogenannten Feldvektors veranschaulicht werden. Die Länge des Vektors ist ein Maß für die Stärke der Kraft, die auf eine Probeladung in diesem Punkt wirken würde, d.h. die Vektorlänge beschreibt den Betrag von . Die Richtung des Vektors steht für die Richtung einer möglichen Kraftwirkung auf eine Probeladung, also für die Richtung des -Feldes im betrachteten Punkt. Die Richtung der Kraftwirkung hängt natürlich von den Vorzeichen der felderzeugenden Ladung und der Probeladung ab. Das -Feld selbst ist unabhängig von der Probeladung. Deswegen wurde die Konvention getroffen, dass in einem elektrostatischen Feld die Richtung der Feldvektoren stets von einer positiven Ladung wegführt und zu einer negativen Ladung hinführt. Die Richtung der Feldvektoren gibt also die Richtung der Kraft an, die auf eine positive Probeladung wirkt. Jedem Punkt eines elektrischen Feldes kann solch ein Feldvektor zugeordnet werden. Die Gesamtheit der Feldvektoren ergibt ein charakteristisches Bild für das elektrische Feld.
Feldlinien des elektrischen Felds (!)
Neben der Darstellung des elektrischen Feldes in Form eines Gitters von Vektorpfeilen wird auch häufig eine Visualisierung mit Hilfe von Feldlinien gewählt. In jedem räumlichen Punkt kann die Tangente an diese Feldlinie betrachtet werden, um die Richtung des elektrischen Felds an dem jeweiligen Ort zu finden. Die Dichte der Feldlinien ist proportional zum Betrag der elektrischen Feldstärke. Je enger die Feldlinien bei einander liegen, umso stärker ist das elektrische Feld.
In der folgenden animierten Skizze können Sie zwischen der Darstellung des elektrischen Felds mit Feldvektoren und der Darstellung durch Feldlinien auswählen. Sie können die beiden Punktladungen verschieben und ihre Ladung variieren. Man erkennt, dass die Feldlinien stets tangential zu den Feldvektoren verlaufen. Die Zahlen dienen nur der Orientierung und haben keine physikalische Bedeutung. Durch die Knöpfe unterhalb der Grafik können Darstellungen hinzugeschaltet werden.
Test
Video 10: Elektrische Felder in ausgedehnten Körpern (C)
.
Video 11: Der Faraday-Käfig (C)
.
Video 12: Elektrische Felder an Oberflächen (C)
.
Weitere Eigenschaften der Feldlinien
In der Elektrostatik haben die Feldlinien immer einen Anfang und ein Ende. Sie verlaufen von den positiven Ladungen zu den negativen Ladungen. Die Richtung der Feldlinien gibt also die Richtung der Kraft an, die auf eine positive Probeladung wirkt.
In elektrostatischen Feldern gibt es keine in sich geschlossenen Feldlinien, ansonsten würden Ladungen beim wiederholten Durchlaufen dieser Schleifen unbegrenzt an Energie gewinnen.
Elektrische Feldlinien schneiden sich nicht. Sonst wäre im Schnittpunkt die Richtung des elektrischen Felds nicht definiert.
Auf den Oberflächen von Körpern, die elektrische Leiter sind, stehen die elektrischen Feldlinien immer senkrecht. Andernfalls würde an der Oberfläche des Leiters eine Komponente parallel zur Oberfläche auftreten, die die im elektrischen Leiter freien Ladungen so verschieben würde, bis das von ihnen erzeugte elektrische Feld wieder senkrecht auf der Oberfläche steht.
Das Innere von elektrischen Leitern ist feldfrei. Sonst würde auf die Ladungen im elektrischen Leiter eine Kraft wirken und diese so lange verschieben, bis sich die räumliche Verteilung der Ladungen so eingestellt hat, dass das elektrische Feld im Inneren des elektrischen Leiters verschwindet. Auch das Innere von elektrisch leitenden Hohlkörpern ist feldfrei. Einen solchen Körper nennt man einen Faraday'schen Käfig.
Wichtig: Elektrische Feldlinien entsprechen nicht den Bahnkurven von (Probe-)Ladungen im elektrischen Feld an.
In der Elektrostatik haben die Feldlinien immer einen Anfang und ein Ende. Sie verlaufen von den positiven Ladungen zu den negativen Ladungen. Die Richtung der Feldlinien gibt also die Richtung der Kraft an, die auf eine positive Probeladung wirkt.
In elektrostatischen Feldern gibt es keine in sich geschlossenen Feldlinien, ansonsten würden Ladungen beim wiederholten Durchlaufen dieser Schleifen unbegrenzt an Energie gewinnen.
Elektrische Feldlinien schneiden sich nicht. Sonst wäre im Schnittpunkt die Richtung des elektrischen Felds nicht definiert.
Auf den Oberflächen von Körpern, die elektrische Leiter sind, stehen die elektrischen Feldlinien immer senkrecht. Andernfalls würde an der Oberfläche des Leiters eine Komponente parallel zur Oberfläche auftreten, die die im elektrischen Leiter freien Ladungen so verschieben würde, bis das von ihnen erzeugte elektrische Feld wieder senkrecht auf der Oberfläche steht.
Das Innere von elektrischen Leitern ist feldfrei. Sonst würde auf die Ladungen im elektrischen Leiter eine Kraft wirken und diese so lange verschieben, bis sich die räumliche Verteilung der Ladungen so eingestellt hat, dass das elektrische Feld im Inneren des elektrischen Leiters verschwindet. Auch das Innere von elektrisch leitenden Hohlkörpern ist feldfrei. Einen solchen Körper nennt man einen Faraday'schen Käfig.
Wichtig: Elektrische Feldlinien entsprechen nicht den Bahnkurven von (Probe-)Ladungen im elektrischen Feld an.
Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Verwenden Sie und .
Verwenden Sie und .