2. Elektromagnetismus
  3. Strom und Magnetismus
  4. Lorentz-Kraft (!),(*)

5.2.3 Lorentz-Kraft





 

Noch kein Basiswissen vorhanden ...
Zu diesem Abschnitt gibt es leider noch kein Basiswissen.

Video 10: Die Lorentz-Kraft (C) .



Wie wir gesehen haben, erzeugt ein stromdurchflossener Leiter ein Magnetfeld, andererseits erfährt ein stromdurchflossener Leiter in einem äußeren Magnetfeld eine Kraft. Mikroskopisch betrachtet bedeutet ein elektrischer Strom, dass Ladungsträger, in der Regel Elektronen, sich bewegen. Das heißt, dass die bewegten Ladungen im Magnetfeld diese Kraft erfahren.

 

Herleitung der Lorentz-Kraft (!)


Im Bild ist ein Schnitt durch einen stromdurchflossenen Leiter dargestellt. Die Elektronen bewegen sich nach rechts, dargestellt durch den Geschwindigkeitspfeil bzw. der Richtung des Elektronenstroms I nat . Die technische Stromrichtung I ist dann entgegengesetzt.
Im Fall einer konstanten Stromstärke I gilt für die Ladung Q, die in der Zeit t durch die Querschnittsfläche A fließt:

I= Q t  .



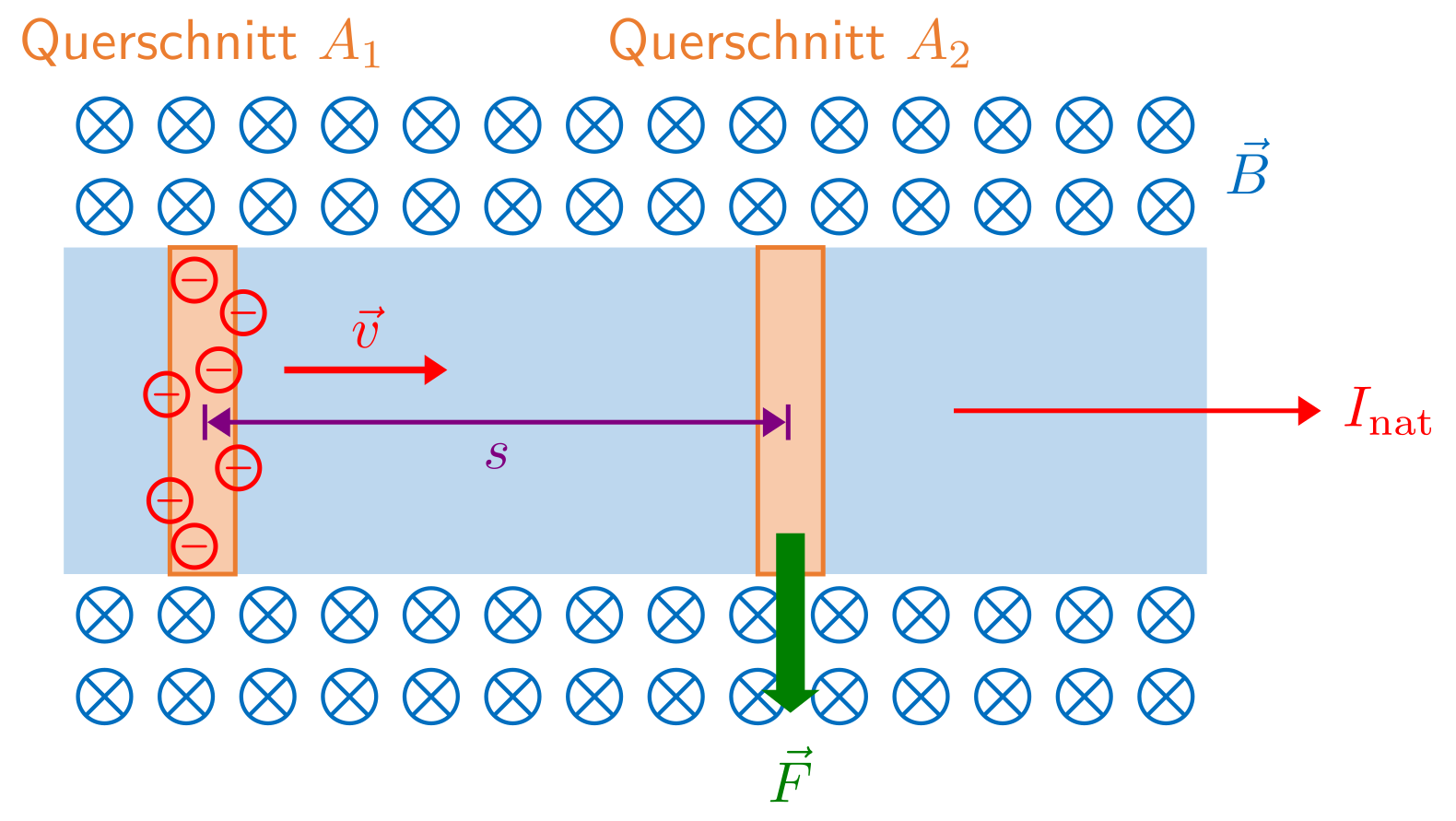
./_25CD13E4_4x.png
Abbildung 5.2.43: Schnitt durch einen stromdurchflossenen Leiter im Magnetfeld  (C)



Nehmen wir an, zum Zeitpunkt t1 =0 s fließt eine Anzahl von N Elektronen durch die Fläche A1 . Alle Elektronen haben dieselbe Geschwindigkeit v. Dann müssen alle gleichzeitig durch eine zweite Fläche A2 fließen, und zwar nach einer Zeit

t2 = s v  .

Die Gesamtladung, die durch die Fläche A1 bzw. A2 fließt, ist Q=N·(-e). Also ist der Strom

I=- I nat = Q t2 =Q· v s  .

Einsetzen in die Gleichung für die Kraft liefert
 
F=B·I·s ​ =B·Q· v s ·s ​ =B·Q·v .
 
Für ein einzelnes Elektron erhält man daraus die Gleichung für die Lorentz-Kraft:

F L =(-e)·v·B .



Video 11: Vektorielle Betrachtung der Lorentz-Kraft (C) .

 

Vektorielle Betrachtung (*)


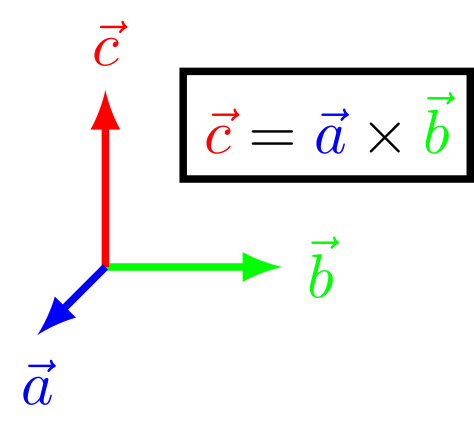
Bisher haben wir unberücksichtigt gelassen, dass die Kraft ein Vektor ist. Aus weitergehenden experimentellen Untersuchungen folgt, dass die Kraft sowohl senkrecht zum Magnetfeld als auch senkrecht zur Bewegungsrichtung der Elektronen steht. Dies lässt sich darstellen durch das Vektor- oder Kreuzprodukt:
c → ⊥ a → und c → ⊥ b → ;  
./_8A0E5F15_4x.png
Abbildung 5.2.44: Kreuzprodukt  (C)

Zur Erinnerung:
 
c → =( c1 c2 c3 )= a → × b →   ​ =( a2 b3 - a3 b2 a3 b1 - a1 b3 a1 b2 - a2 b1 ) ;
 
a → , b → und c → bilden ein Rechtssystem.

Wir notieren jetzt also die
Lorentz-Kraft in Vektor-Schreibweise  


F → L =Q·( v → × B → ) .

Diese Gleichung gilt so für positive Ladungen. Die Richtung der Kraft kann man mit der Rechte-Hand-Regel bestimmen:

././Physikkurs/strommagnetisch_lorentzkraft/images/strommagnetisch_lorentzkraft_RechteHandRegel.png
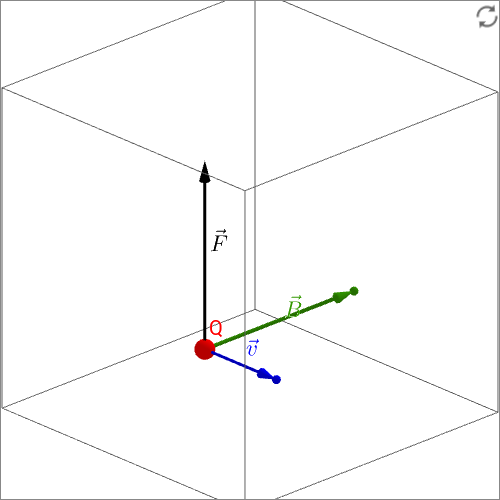
Abbildung 5.2.45: Bestimmung der Richtung der Lorentz-Kraft (C)



Aufgrund der negativen Ladung gilt für ein Elektron:

F → L =-e·( v → × B → ) .

Die Kraft auf ein bewegtes Elektron zeigt also genau entgegen der Kraft, die auf eine genauso bewegte positive Ladung im selben Magnetfeld wirken würde. Dies zeigt sich am Minuszeichen in der obigen Herleitung.

Allgemein ist der Betrag eines Vektorprodukts

| a → × b → |=| a → |·| b → |·sin(φ)

mit φ = Winkel zwischen a → und b → . Da jedoch in unserem Fall auch Strom und Magnetfeld senkrecht zueinander stehen, ist sin(φ)=1, und wir dürfen schreiben:

F L =B·Q·v .

Da die Lorentz-Kraft immer senkrecht zur Geschwindigkeit der Ladungsträger wirkt, bewirkt sie keine Änderung des Geschwindigkeitsbetrags. Die Ladungsträger gewinnen oder verlieren keine Energie. Der Geschwindigkeitsbetrag von Ladungsträgern kann nur in einem elektrischen Feld verändert werden.

Die interaktive GeoGebra-Skizze verdeutlicht den Sachverhalt für eine positive Ladung:

././Physikkurs/strommagnetisch_lorentzkraft/images/geogebra_strommagnetisch_standbild1.png
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)

Video 12: Bewegung von Ladungsträgern im Fadenstrahlrohr (C) .



Video 13: Fadenstrahlrohr: Beispiel (C) .



Bewegung von Ladungsträgern  
Die Lorentz-Kraft wirkt immer senkrecht zur Bewegungsrichtung der Ladung. Was bedeutet das, wenn eine (im unteren Bild negative) Ladung ihrerseits senkrecht zu einem Magnetfeld in dieses einfliegt?

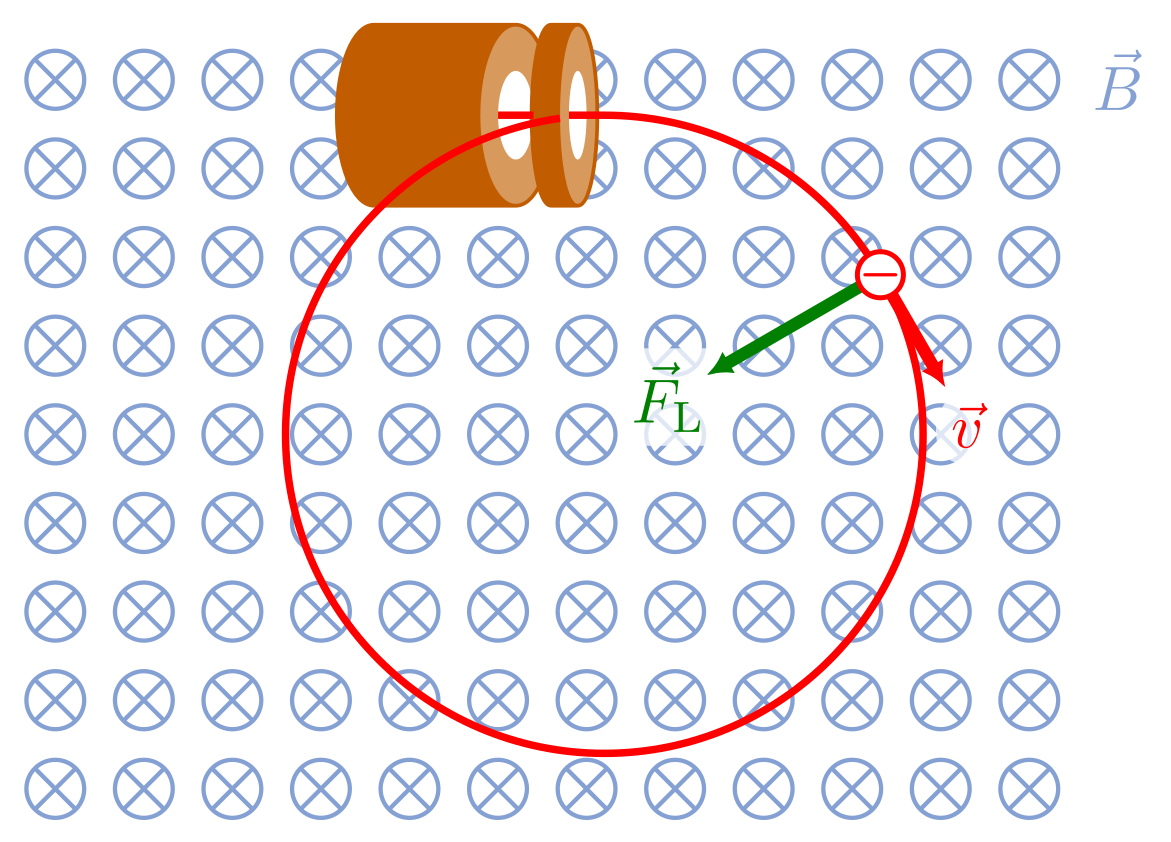
./_E028C7FC_4x.png
Abbildung 5.2.47: Kreisbahn negativer Ladungen im Magnetfeld  (C)



Sobald die Ladung, z.B. ein Elektron, beim Einflug ins Magnetfeld bereits eine Geschwindigkeit v hat, wird es von der Lorentz-Kraft senkrecht dazu abgelenkt und ändert geringfügig seine Richtung (nicht den Betrag der Geschwindigkeit!). Die Lorentz-Kraft ändert dann auch wieder ihre Richtung, weil sie immer senkrecht zur Geschwindigkeit wirkt. Das Elektron folgt der Kraftwirkung und wird wieder etwas abgelenkt usw. Das Ergebnis ist eine Kreisbahn.

Lorentz-Kraft = Zentripetal-Kraft:
 
e·v·B= m· v2 r   ⟺   r= m·v e·B  .
 
Da in dieser Gleichung der mechanische Impuls m·v steht, werden Magnetfelder auch als Impulsfilter bezeichnet, denn durch Bestimmung des Kreisbahn-Radius r kann man den Impuls des Teilchens bestimmen.


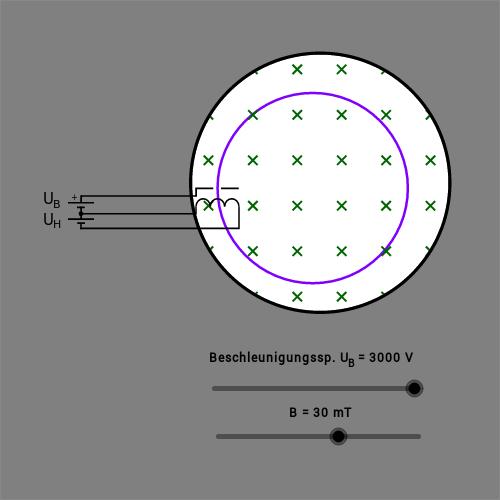
././Physikkurs/strommagnetisch_lorentzkraft/images/geogebra_strommagnetisch_standbild2.png
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)

Die interaktive GeoGebra-Skizze zeigt ein sogenanntes Fadenstrahlrohr: Ein Elektron wird durch eine Beschleunigungsspannung U B zunächst beschleunigt (wie bei der Braun’schen Röhre), ehe es in ein Magnetfeld B einfliegt. In diesem Magnetfeld wird es auf eine Kreisbahn mit dem Radius r abgelenkt.

Wenn wir für die Geschwindigkeit verwenden:
 
e· U B = 1 2   me · v2   ⟹   v= 2 eU B me  ,
 
erhalten wir eine Beziehung für die Elektronenmasse aus der Größe des Radius:

me = e r2 B2 2 U B  .



Beispiel 5.2.18  
Die Elektronenmasse beträgt ungefähr 9,1· 10-31  kg, die Elementarladung 1,6· 10-19  C. Bei einer Beschleunigungsspannung U B =10 kV und einem Magnetfeld B=1 mT ergibt sich:
 
r= me e   2 U B B2 =​ 9,1· 10-31  kg 1,6· 10-19  C · 2·10000 V (0,001 T )2 ​ ≈0,34 m=34 cm ;
 
kurze Betrachtung der Einheiten unter der Wurzel:
 
N= V·C m = kg·m s2   ⟹   kg=V·C· s2 m2  ;   T= V·s m2  ;
kg C · V T2 =​ V·C· s2 m2 C · V ( V·s m2 )2 ​ = m2  .
 




Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Verwenden Sie e=1,602· 10-19  C und μ0 =4π· 10-7   T m A .