4.1.7 Kraftwandler
Video 30: Begriffsdefinition Kraftwandler (C)
.
Prinzip der Kraftwandler (!)
Beispiele sind:
- Das Seil, das den Angriffspunkt der Kraft verschiebt.
- Die Rolle, die die Richtung der Kraft verändert.
- Der Hebel, der die Richtung und die Größe der Kraft ändern kann.
- Der Keil, der die Richtung und die Größe der Kraft ändert.
Die Änderung des Angriffspunkts und der Richtung einer Kraft durch die verschiedenen Kraftwandler ergeben sich direkt aus deren Geometrie. Die Änderung der Größe der Kraft beruht auf der Goldenen Regel der Mechanik, die Galilei so formulierte:
„Was man an Kraft spart, muss man an Weg zusetzen.“ (Wikipedia)
Wir untersuchen diese Regel nun an Hand von verschiedenen Beispielen.
Hebel (!)
Video 31: Balkenwaage und Hebelgesetz (C)
.
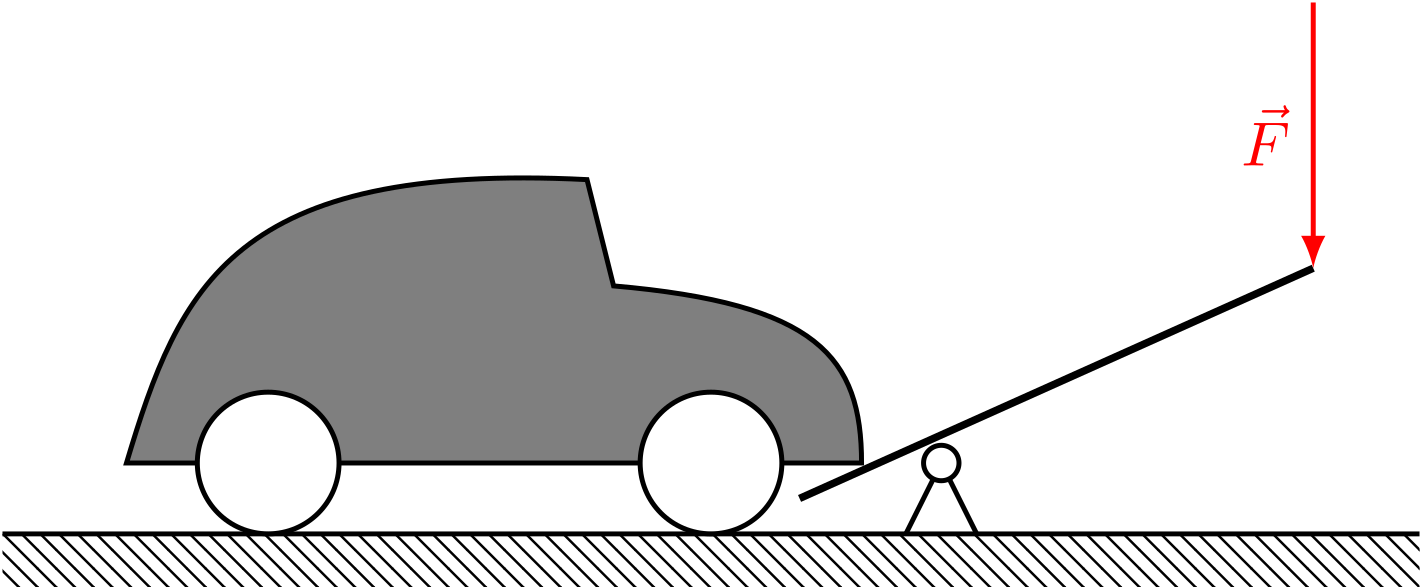
Abbildung 4.1.314: Anheben eines Autos mit einem Hebel (C)
Ein Hebel ist eine lange Stange, die in einem Drehpunkt gelagert ist. Wirkt eine Kraft seitlich auf eine Stelle der Stange, so wirkt im Gleichgewicht an allen anderen Angriffspunkten der Stange ebenfalls eine Kraft. Man verschiebt also mit einem Hebel zum einen den Angriffspunkt der Kraft. Zum anderen hängt die Größe der übertragenen Kraft von der Entfernung vom Drehpunkt ab. Hier betrachtet man wieder das Goldene Gesetz der Mechanik. In der unten stehenden Skizze ist ein einfacher Hebel gezeichnet. Die Kraft greift in einem vorgegebenen Abstand zum Drehpunkt am Hebel an und erzeugt die Kraft . Dreht sich der Hebel nun um den Drehpunkt, so legt der Angriffspunkt der kleineren Kraft eine längere Wegstrecke, nämlich den Kreisbogen , zurück als der Angriffspunkt der größeren Kraft , der eine kürzere Wegstrecke, nämlich den Kreisbogen , zurücklegt.
In der interaktiven Skizze kann nicht nur der Hebel bewegt werden, es kann auch der Angriffspunkt der Kraft entlang des Hebels verschoben werden, während der Betrag von unverändert bleibt. Je kürzer man den Hebelarm der Kraft wählt, umso kleiner muss die aufzuwendende Kraft sein. Ziehen Sie den Angriffspunkt von auch auf die Seite des Angriffspunktes von hinüber und beobachten Sie, wie sich die Richtung ändert.
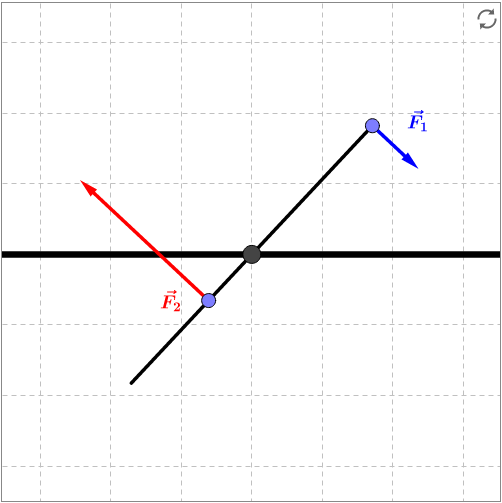
Hebelgesetz

Wird ein Hebel auf beiden Seiten mit unterschiedlichen Kräften und senkrecht belastet, so befindet sich er sich im Gleichgewicht, wenn das Hebelgesetz
erfüllt ist. Hierbei sind und die Abstände der Angriffspunkte der Kräfte vom Drehpunkt des Balkens.

Abbildung 4.1.316: Hebelgesetz (C)
Wird ein Hebel auf beiden Seiten mit unterschiedlichen Kräften und senkrecht belastet, so befindet sich er sich im Gleichgewicht, wenn das Hebelgesetz
erfüllt ist. Hierbei sind und die Abstände der Angriffspunkte der Kräfte vom Drehpunkt des Balkens.
Da beim Hebel die Kraft nicht direkt am Drehpunkt angreift, wird ein sogenanntes Drehmoment erzeugt.
Das Drehmoment ist das Produkt aus Kraft und Hebelarm :
Sind Hebel und Kraft nicht senkrecht zueinander, ist dies über den Faktor zu berücksichtigen. Dabei ist () der Winkel zwischen Hebel und Kraft,
Die Einheit des Drehmoments ist .
Das Drehmoment ist eine vektorielle Größe. Es steht senkrecht auf der Ebene, die von und aufgespannt wird. Die Richtung kann mit der bestimmt werden. Details sind im Kapitel 4.5.2 gegeben.
Sind Hebel und Kraft nicht senkrecht zueinander, ist dies über den Faktor zu berücksichtigen. Dabei ist () der Winkel zwischen Hebel und Kraft,
Die Einheit des Drehmoments ist .
Das Drehmoment ist eine vektorielle Größe. Es steht senkrecht auf der Ebene, die von und aufgespannt wird. Die Richtung kann mit der bestimmt werden. Details sind im Kapitel 4.5.2 gegeben.
Im Alltag trifft man häufig auf Geräte, die die Hebelwirkung nutzen. Ein Beispiel ist der im Foto abgebildete Seitenschneider, bei der die Kraft, die auf einen Draht wirkt, sehr viel größer ist als die Kraft, die man mit der Hand aufwendet. Darüber hinaus sind die Schneiden keilförmig und erleichtern zusätzlich das Schneiden. Das Beispiel des Seitenschneiders entspricht der Situation in der obigen Skizze, bei der die Angriffspunkte der Kräfte auf verschiedenen Seiten des Drehpunkts liegen (zweiseitiger Hebel).
Ein weiteres Beispiel ist der klassische Nussknacker (siehe Foto). Hier wird die Kraft der Hand verstärkt, um die Nuss zu knacken. In diesem Fall liegen die Angriffspunkte der beiden Kräfte auf der gleichen Seite des Drehpunkts (einseitiger Hebel).

Abbildung 4.1.317: Das Hebelgesetz im Alltag: Seitenschneider (zweiseitiger Hebel) und Nussknacker (einseitiger Hebel) (C)
Video 32: Beispiel zum Hebelgesetz (C)
.
Beispiel
4.1.67
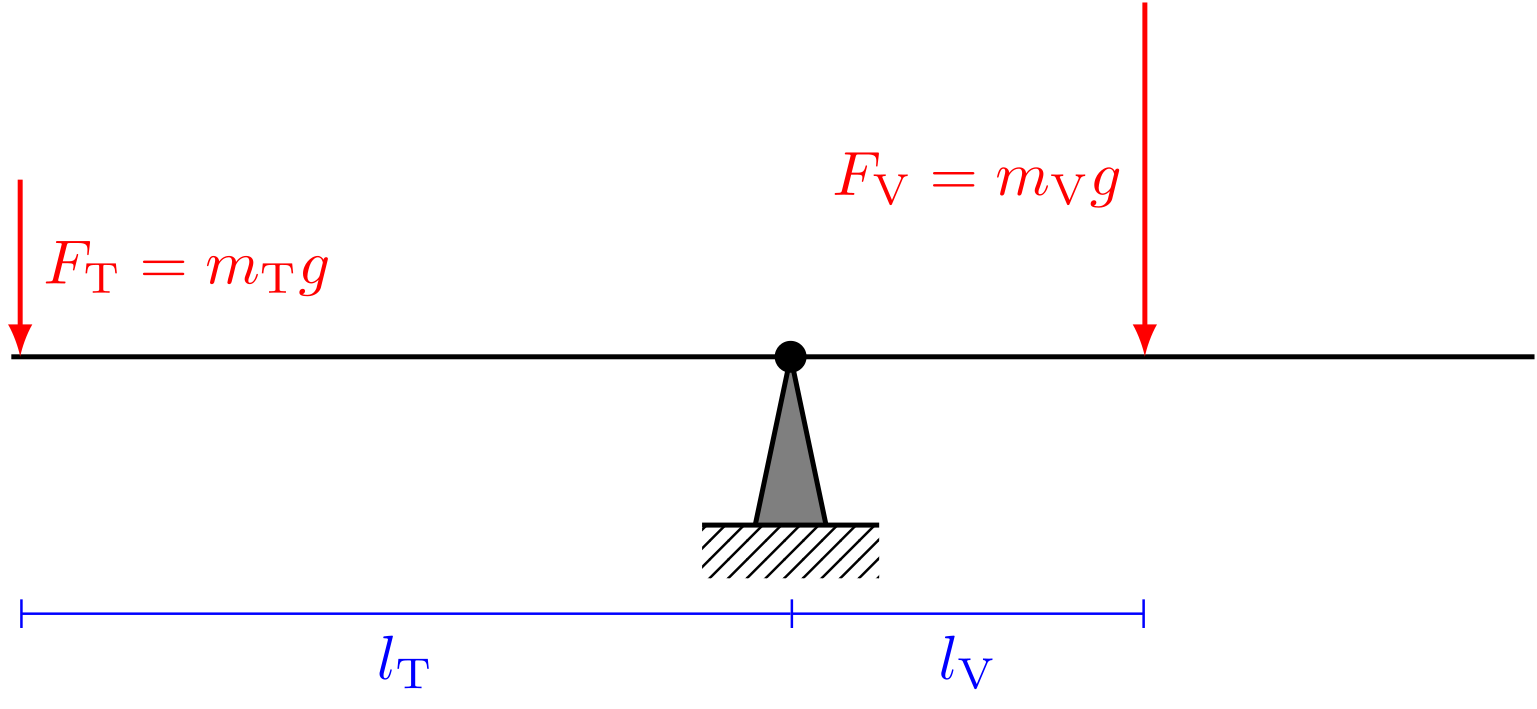
Ein Vater () spielt mit seiner Tochter () auf einem Spielplatz. Die Tochter sitzt auf einer Wippe im Abstand vom Drehpunkt. In welchem Abstand vom Drehpunkt muss der Vater sitzen, damit die Wippe im Gleichgewicht ist?
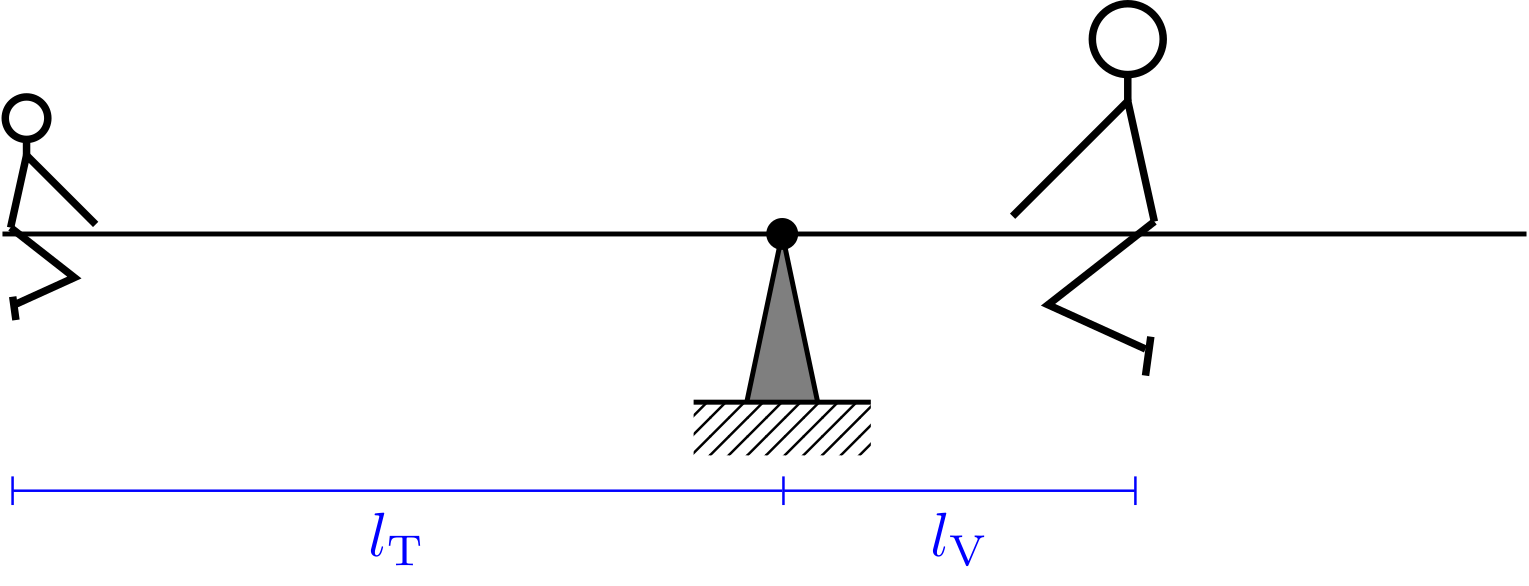
Ein Vater () spielt mit seiner Tochter () auf einem Spielplatz. Die Tochter sitzt auf einer Wippe im Abstand vom Drehpunkt. In welchem Abstand vom Drehpunkt muss der Vater sitzen, damit die Wippe im Gleichgewicht ist?

Abbildung 4.1.318: Vater und Tochter auf der Wippe (C)
Video 34: Seil und Seil mit fester Rolle (C)
.
Seil (!)
Beispiel
4.1.68
Mit einem Seil kann der Angriffspunkt einer Kraft verschoben werden:
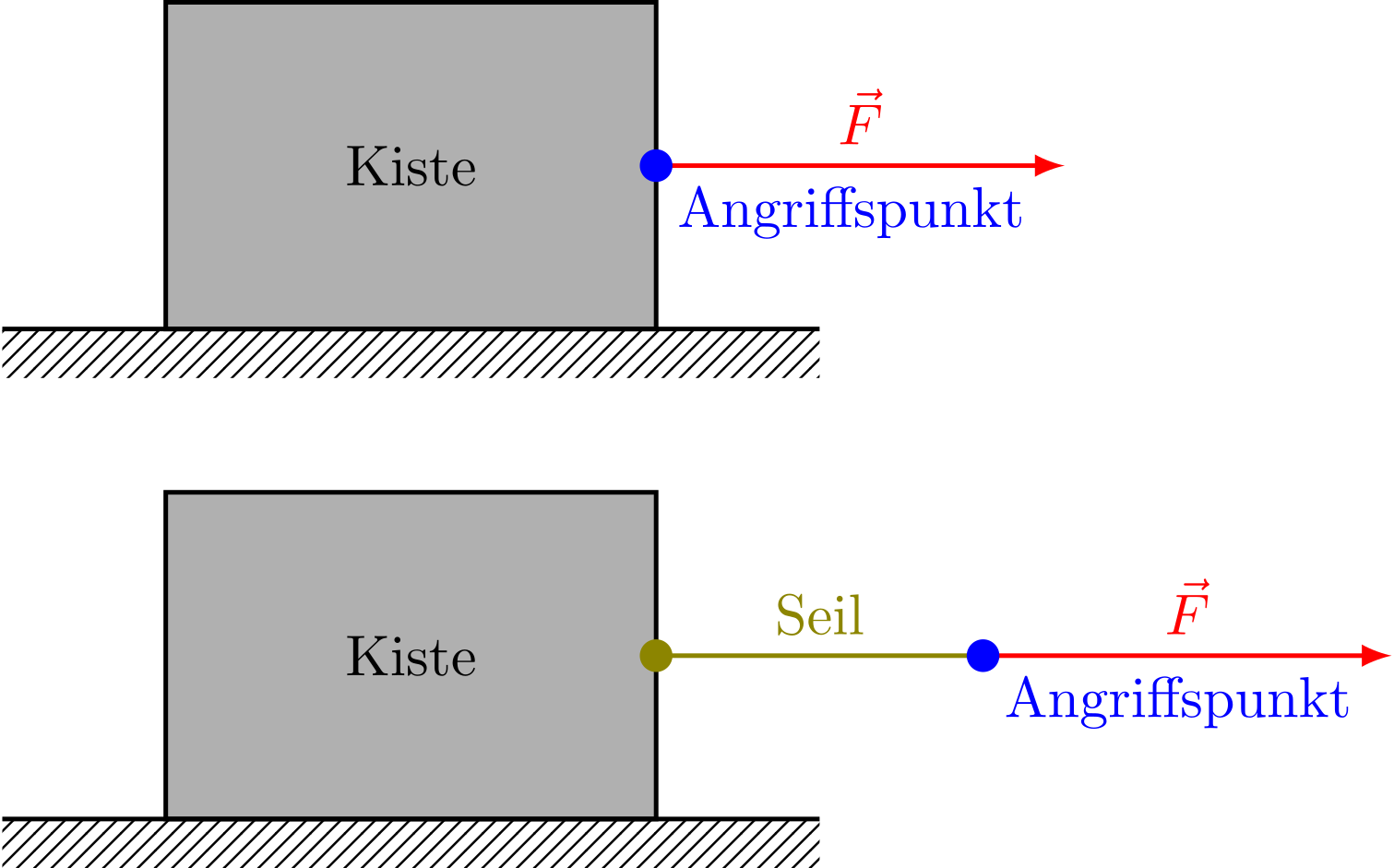
Mit einem Seil kann der Angriffspunkt einer Kraft verschoben werden:

Abbildung 4.1.320: Verschiebung des Angriffspunktes mit einem Seil (C)
Seil mit fester Rolle (!)
Die Rolle ändert die Richtung der Seilkraft. Man stelle sich z.B. eine Rolle vor, die im Raum fixiert ist und über die ein Seil geführt wird. Das Seil soll an beiden Seiten der Rolle herabhängen, wobei an einem Ende des Seils ein Körper befestigt ist. Zieht man nun am anderen Seilende, wird der Körper angehoben. Die Richtung der Kraft wurde also geändert, denn man zieht nach unten, aber der Körper wird angehoben. Die übertragene Kraft bleibt aber gleich.
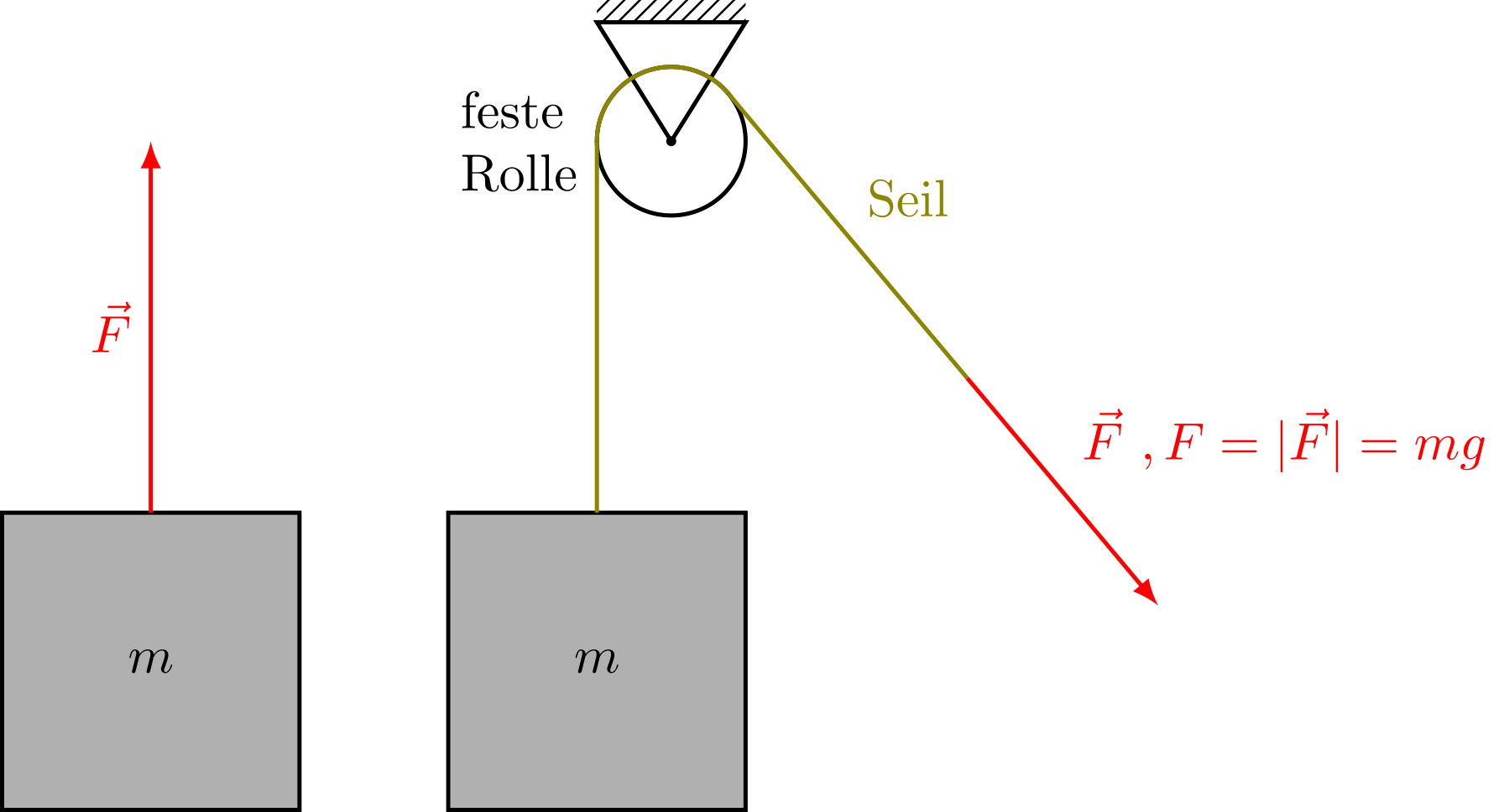
Abbildung 4.1.321: Seil mit fester Rolle (C)
Flaschenzug (+)
Video 35: Flaschenzug mit einer festen und einer losen Rolle (C)
.
Mit einer festen und einer losen Rolle kann man die einfachste Form eines Flaschenzugs aufbauen (siehe folgende Skizze). An der losen Rolle hängt eine Last, die durch Ziehen an dem Seil, das über die feste Rolle geführt wird, gehoben werden soll. Die Gewichtskraft der Last wird über die lose Rolle auf die beiden Seile übertragen. In jedem Seil wirkt die halbe Gewichtskraft. Man muss also nur mit der halben Gewichtskraft am Seilende ziehen, um die Last anzuheben.
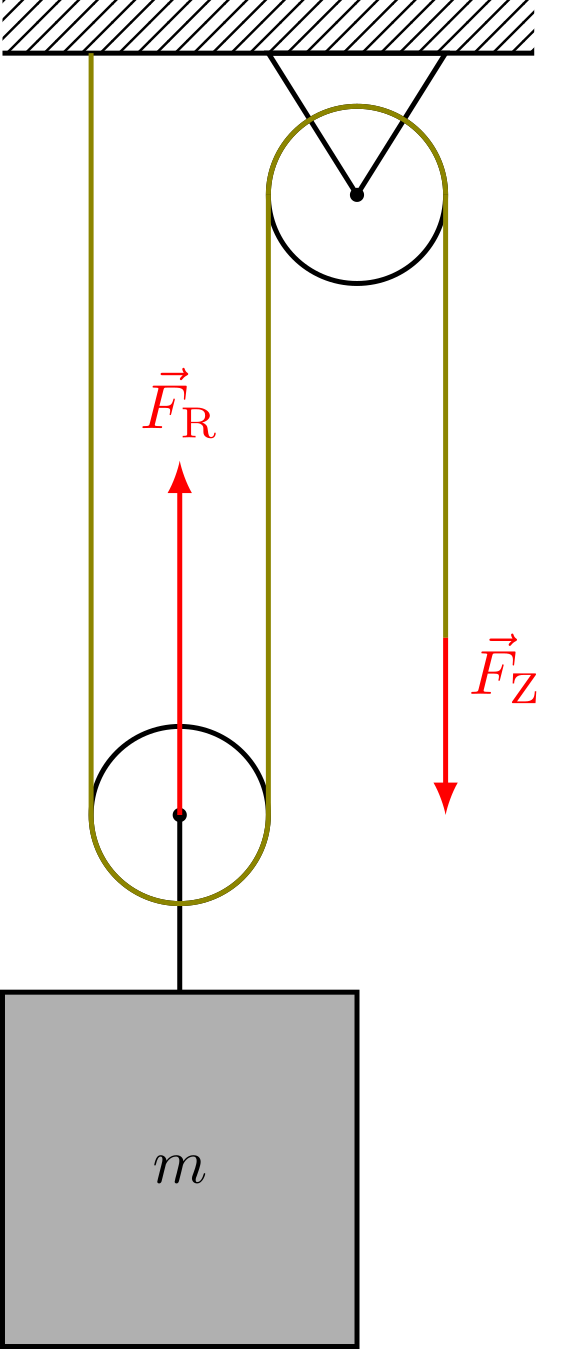
Abbildung 4.1.322: Flaschenzug (C)
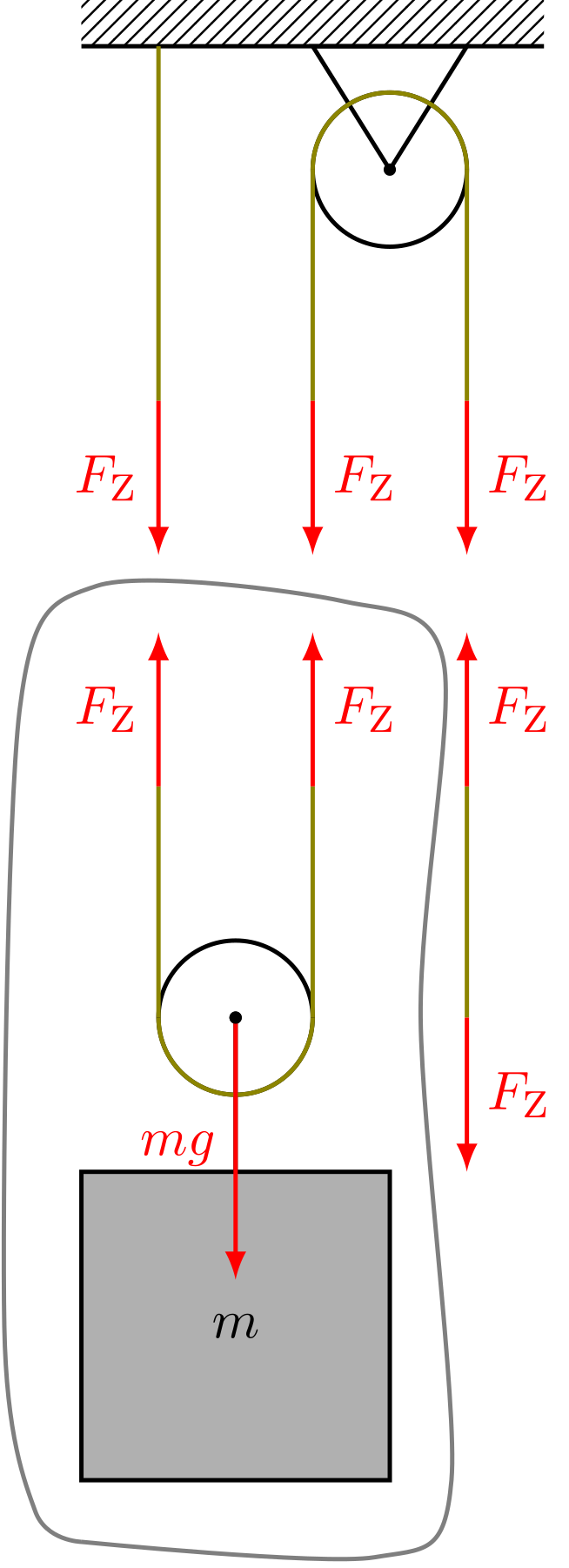
Abbildung 4.1.323: Flaschenzug Kräfte (C)
Anhand der Geometrie sieht man auch, dass man für das Anheben der Last um eine gewisse Strecke die doppelte Strecke am Seil ziehen muss. Damit ist das Goldene Gesetz der Mechanik erfüllt, denn die Halbierung der Kraft entspricht der Verdoppelung der Zugstrecke.
Das Prinzip des Flaschenzugs können Sie sich an folgender interaktiver Skizze veranschaulichen. Durch Ziehen am blauen Punkt können Sie die Last anheben. Die Strecke, um die Sie ziehen müssen, ist gerade doppelt so groß wie die Höhe, auf die die Last damit angehoben wird.
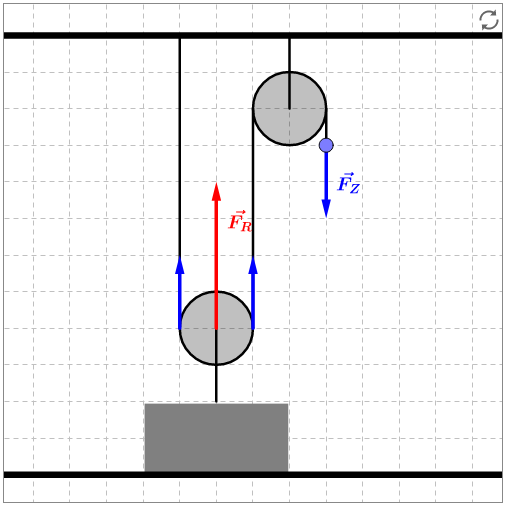
Video 36: Flaschenzug mit festen und losen Rollen (C)
.
Das Prinzip des Flaschenzugs kann auch für mehr als eine lose Rolle angewendet werden. Die Gewichtskraft der Last verteilt sich dann auf alle Seile, die von den losen Rollen abgehen. Die benötigte Zugkraft zum Heben der Last ergibt sich dann zu
Hierbei sind die Gewichtskraft der Last und die Zahl der losen Rollen. Auf den beiden Fotos sind technische Realisierungen von Flaschenzügen zu sehen. Dies ist zum einen der Flaschenzug eines Kranhakens, der zwei lose Rollen besitzt, zum anderen ein Flaschenzug auf einem Segelschiff, in dem drei lose Rollen verbaut sind.

Abbildung 4.1.325: Flaschenzug eines Kranhakens (C)

Abbildung 4.1.326: Flaschenzug einer Schiffstakelage (C)
Keil (*)
Video 37: Kraftverstärkung mit einem Keil (C)
.
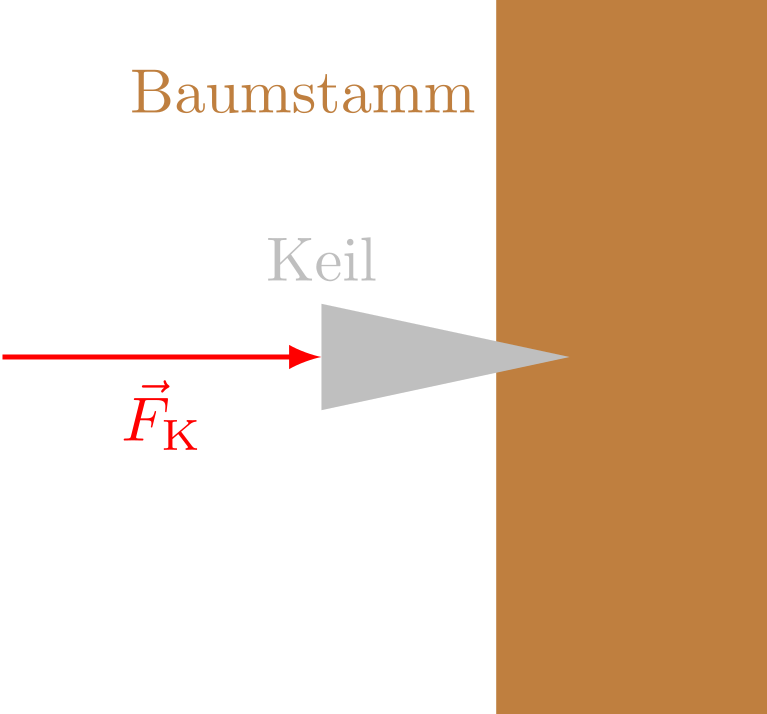
Abbildung 4.1.327: Keil als Kraftwandler (C)
Ein Keil ist ein Kraftwandler, bei dem eine kleine Kraft längs des Keils in eine viel größere Kraft senkrecht zum Keil umgewandelt wird. Die Vergrößerung der Kraft kann man sich an Hand des Kräfteparallelogramms in der folgenden interaktiven Skizze klarmachen. In diesem Fall ist das Kräfteparallelogramm ein Rechteck. Die Kraft , die der Keil auf das Werkstück ausübt, steht senkrecht auf der oberen Fläche des Keils. Auch hier kann man wieder das Goldene Gesetz der Mechanik anwenden. Die große Kraft , die der Keil auf ein Werkstück ausübt, ist mit einer sehr kleinen Wegstrecke verbunden, um die das Werkstück bei der Bewegung des Keils zur Seite hin verschoben wird. Um dies zu sehen, können Sie den Keil in der Skizze durch Ziehen an dem unteren blauen Punkt nach rechts verschieben. Verändern Sie auch den Keilwinkel, indem Sie den oberen blauen Punkt nach oben oder unten ziehen.
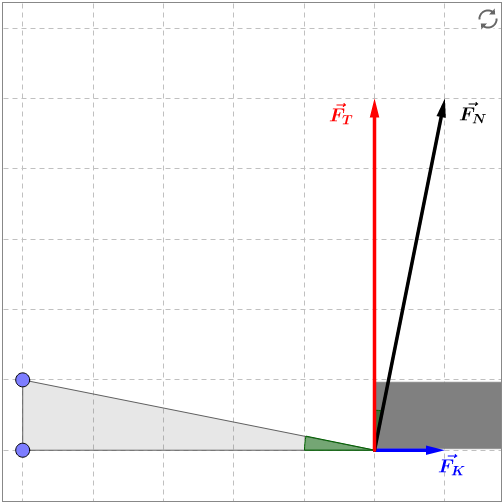
Ein bekanntes Beispiel für die Nutzung eines Keils ist das Spalten eines Holzstücks. Die keilförmige Schneide einer Axt verstärkt die im Hieb liegende Kraft zu einer sehr viel stärkeren transversalen Kraft, die das Holzstück spaltet.

Abbildung 4.1.329: Spaltaxt (C)
Übersetzung (*)
Drehungen von kreisförmigen Scheiben, vgl. auch Drehbewegungen in Abschnitt 4.5.1, können mechanisch miteinander gekoppelt werden. Dies kann entweder durch direkte Berührung (Reibung) bzw. über Zahnräder oder auch über nicht rutschende Bänder bzw. Keilriemen oder Ketten geschehen. Dabei werden jeweils die zurückgelegten Wege auf dem Rand der Scheibe miteinander gleichgesetzt: Dreht sich eine Scheibe mit Radius insgesamt Mal, so dreht sich eine direkt gekoppelte Scheibe mit Radius insgesamt Mal. Die zurückgelegten Umfangswege sind dabei und . Gleichgesetzt liefern sie die Beziehung
Das so berechnete Verhältnis ist das sogenannte Übersetzungsverhältnis der beiden kreisförmigen Scheiben. Bei Zahnrädern wird dann anstelle des Verhältnisses der Radien das Verhältnis der Zähnezahlen der Scheiben verwendet. Mit längs einer Achse fest verbundenen parallelen Scheiben lassen sich darüber hinaus in mehrstufigen Anordnungen kompliziertere Getriebe mit größeren Übersetzungsverhältnissen konstruieren. Das gesamte Übersetzungsverhältnis erhält man dann als Produkt der einzelnen Übersetzungsverhältnisse.
Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie .
Falls nicht anders angegeben, verwenden Sie