2. Wärmelehre
  3. Thermodynamische Prozesse (*)
  4. Zustandsänderungen des idealen Gases (+)

7.2.1 Zustandsänderungen des idealen Gases





 

Noch kein Basiswissen vorhanden ...
Zu diesem Abschnitt gibt es leider noch kein Basiswissen.  

Die Zustandsgleichung des idealen Gases (+)


Video 1: Die Zustandsgleichung des idealen Gases (C) .



Als ideales Gas bezeichnet man ein Gas, in dem man die Gasmoleküle näherungsweise als Massenpunkte ansehen kann, die nur durch elastische Stöße miteinander und mit anderen Objekten (z.B. Wänden) wechselwirken. Anziehungskräfte zwischen den Gasmolekülen werden also ebenso vernachlässigt wie die innere Struktur der Moleküle und deren Eigenvolumen. Edelgase wie Helium erfüllen diese Voraussetzungen sehr gut. Aber auch andere Gase kann man als ideale Gase behandeln, wenn man sie genügend weit verdünnt. Für ein solches Gas gilt die Zustandsgleichung des idealen Gases:


p V=n R T .

Hierbei sind der Gasdruck p, das vom Gas eingenommene Volumen V und die absolute Temperatur des Gases T die variablen Größen. n ist die Stoffmenge des Gases in Mol (ein Mol sind ca. 6,022· 1023 Teilchen). R bezeichnet die universelle Gaskonstante. Diese hat den Wert:

R=8,31  J mol K  .

Beispiel 7.2.1  
Ein Mol eines idealen Gases nimmt bei Normwerten ( 0 ∘ C, Atmosphärendruck) ein Volumen von 22,4 l ein:
 
V= n R T p ≈​ 1 mol·8,31  J mol K ·273 K 1,013· 105  Pa ​ ≈0,0224  m3 =22,4 l .
 


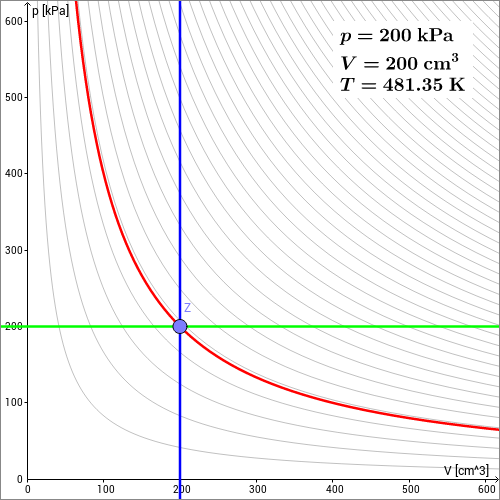
Der Zustand eines idealen Gases kann in einem sogenannten p- V-Diagramm dargestellt werden. Hier ist der Gasdruck p in Abhängigkeit vom Volumen V, welches das Gas einnimmt, aufgetragen. Betrachtet man Zustände mit konstanter Temperatur, gilt p·V= konstant . Daraus folgt:

p(V)= Konstante V  .

Zustände konstanter Temperatur liegen also auf Hyperbeln.  

Dieser Sachverhalt ist in der nächsten animierten Skizze dargestellt. In dem p- V-Diagramm sind als dünne graue Linien die Hyperbeln eingezeichnet, die jeweils Zuständen mit konstanter Temperatur entsprechen. Ein verschiebbarer Punkt Z stellt den Zustand eines idealen Gases dar, das eine Stoffmenge von 0,01 mol enthält. Über die Gasgleichung ist dann bei vorgegebenem Druck p und Volumen V die Temperatur T eindeutig bestimmt. Sehen Sie sich dies an, indem Sie den Zustand durch Bewegen des Punktes Z in der p- V-Ebene variieren.  

././Physikkurs/thermodynamischeprozesse_zustandidealesgas/images/geogebra_thermodynamischeprozesse_standbild4.png
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)

 

Zustandsänderungen eines Gases (+)


Der Zustand eines idealen Gases ist gekennzeichnet durch die drei variablen Größen p, V und T. (Die Stoffmenge des Gases wird für die folgenden Betrachtungen als konstant angenommen.) Eine Zustandsänderung beschreibt den Übergang von einem Zustand 1 (gekennzeichnet durch p1 , V1 und T1 ) in einen Zustand 2 (gekennzeichnet durch p2 , V2 und T2 ). Dabei lassen sich prinzipiell drei Zustandsänderungen unterscheiden:

  • isotherme Zustandsänderung: Die Temperatur wird durch Anbindung an ein äußeres Wärmebad konstant gehalten ( T1 = T2 ). Diese Zustandsänderung wird durch die Hyperbeln in der oben gezeigten Skizze beschrieben.

  • isochore Zustandsänderung: Das Volumen wird konstant gehalten ( V1 = V2 ). Es ändern sich Temperatur und Druck des Gases.

  • isobare Zustandsänderung: Der Druck wird konstant gehalten ( p1 = p2 ). Es ändern sich Temperatur und Volumen.

Wenn eine der Zustandsgrößen verändert wird, ändert sich also immer mindestens eine der anderen Größen ebenfalls. Sind zwei der Größen festgelegt, ist die dritte keine frei wählbare Größe mehr, sondern sie stellt sich gemäß der Gasgleichung ein. Wird beispielsweise bei konstantem Volumen die Temperatur des äußeren Wärmebads geändert, so wird dem Gas Wärmeenergie zugeführt (Temperaturerhöhung) oder entzogen (Temperaturerniedrigung). Dann ändert sich auch der Druck des Gases.

 

Volumenarbeit eines Gases (+)


Video 2: Zustandsänderungen und Volumenarbeit (C) .



Wird das Volumen eines Gases geändert, so muss am Gas Arbeit verrichtet werden (bei Verringerung des Volumens) oder das Gas leistet Arbeit am äußeren System (bei Vergrößerung des Volumens). Diese mechanische Arbeit kann man sich mit Hilfe der folgenden Skizze herleiten:

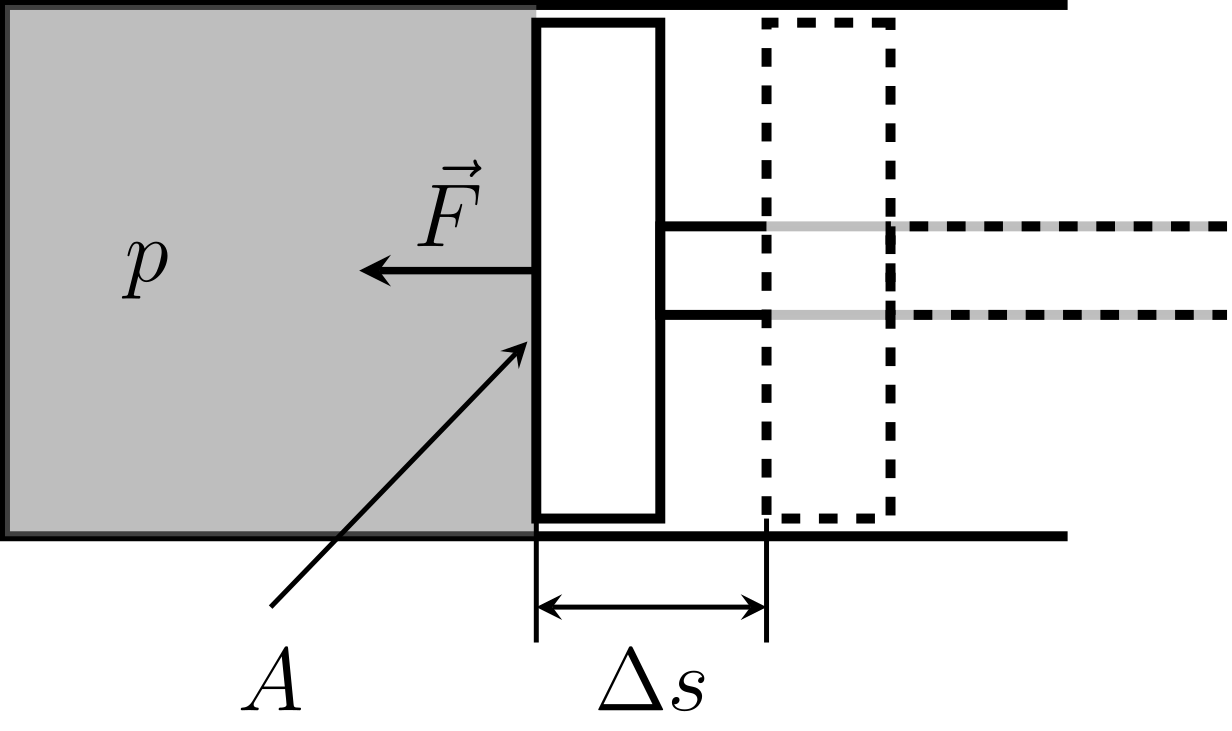
./_252FCFC5_4x.png
Abbildung 7.2.2: Komprimierung eines Gases mittels Kolben  (C)



Man betrachtet die Bewegung eines Kolbens der Fläche A um die Strecke Δs. Δs sei sehr klein, sodass während dieses Prozesses der Druck p des Gases als konstant angenommen werden kann. Aus der Mechanik ist bekannt, dass die durch eine Kraft entlang eines Wegs verrichtete Arbeit gegeben ist durch

W= F → · s → =F·s ,

wenn F und s parallel sind und in die gleiche Richtung zeigen. Nach Definition ist Druck eine Kraft auf eine Fläche:
 
p= F A   ⟺   F=p·A .
 
Das ist die Kraft, die aufgewendet werden muss, um den Kolben zu bewegen. Dabei wird die Arbeit W=F Δs=pA Δs am Gas geleistet. Die dabei erfolgte Volumenänderung ist ΔV= V Ende - V Anfang =-A·Δs. Das Minuszeichen kommt daher, dass sich das Volumen beim Hineindrücken des Kolbens verkleinert.
Man erhält also insgesamt für die am Gas geleistete Arbeit:

W=-p ΔV>0 .

Wird der Kolben herausgezogen, erhält man W<0, da das Gas dann am äußeren System Arbeit verrichtet.
Die obige Beziehung wurde für konstanten Druck p hergeleitet. Ändert sich der Druck während der Volumenänderung, so muss man die Beziehung durch eine Integration ersetzen:

W=- ∫ V1 V2 p(V) dV .



 

Innere Energie und Erster Hauptsatz der Wärmelehre (+)


Video 3: Innere Energie und Erster Hauptsatz der Wärmelehre (C) .



Der Erste Hauptsatz der Wärmelehre ist die Anwendung des Energieerhaltungssatzes auf die Wärmelehre. Wie oben diskutiert, können einem idealen Gas zwei Formen von Energie zugeführt bzw. entzogen werden:
  • Die Wärmemenge Q bezeichnet die Energie, die nur durch statistische elastische Stöße auf das System übertragen wurde, also nur durch Änderung der Temperatur, ohne dass das Volumen sich ändert.

  • Die Volumenarbeit W=-p ΔV bezeichnet die Energie, die dem System durch Kompression/Expansion zugeführt bzw. entzogen wurde. Hierbei kann sich die Temperatur des Systems geändert haben, muss es aber nicht. Die Volumenarbeit berücksichtigt nur die Änderung des Volumens.

Die innere Energie U eines thermodynamischen Systems ist sein gesamter Energieinhalt bezogen auf sein Massenmittelpunktsystem.

Beim idealen Gas trägt bei konstantem Volumen zugeführte Wärme vollständig zur Erhöhung der inneren Energie bei. Damit gilt für ein ideales Gas

U=n CV T

mit der Molzahl n und der molaren Wärmekapazität CV des Gases für die Temperaturänderung bei konstant gehaltenem Volumen. Bei einem einatomigen idealen Gas findet man experimentell CV = 3 2 R. Lässt man auch Volumenänderungen ΔV zu, so ergibt sich folgende Energieerhaltungsgleichung:

Q=ΔU+p ΔV .

Die Zugeführte Wärme teilt sich auf in Erhöhung der inneren Energie und Arbeit. In der Form

ΔU=Q-p ΔV=Q+W

ist das die mathematische Formulierung des Ersten Hauptsatzes für ein ideales Gas

Die innere Energie charakterisiert ein thermodynamisches System vollständig, solange kein Teilchenaustausch stattfindet. Diese Definition gilt nicht nur für ideale Gase. Sie kann auf jedes thermodynamische System angewendet werden. Dann ist W nicht mehr nur die Volumenarbeit, sondern jede Form von Arbeit, die an dem System verrichtet werden kann (z.B. magnetische oder elektrische Arbeit).

Der Erste Hauptsatz der Wärmelehre lautet: Die Änderung der inneren Energie eines Systems ist gleich der Summe aus der zugeführten Wärmemenge Q und der am System geleisteten Arbeit W,

ΔU=Q+W .

Dem Gas entzogene Wärme und vom Gas geleistete Arbeit werden jeweils durch ein negatives Q bzw. W berücksichtigt.