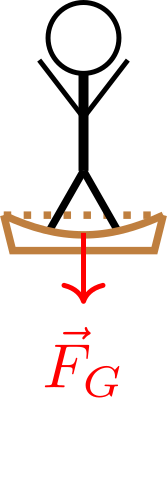
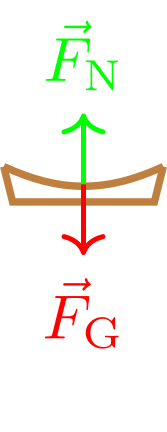
4.1.2 Kräftegleichgewicht
Basiswissen „Schwerpunkt“
Bei der Verwendung von Pfeilen als Symbol für die wirkenden Kräften stellt sich die Frage, wo ein solcher Pfeil sinnvoll an einem Körper verankert wird. Um diese Frage zu beantworten, soll das einfache Modell eines Stabes betrachtet werden, wie in der Skizze dargestellt ist:
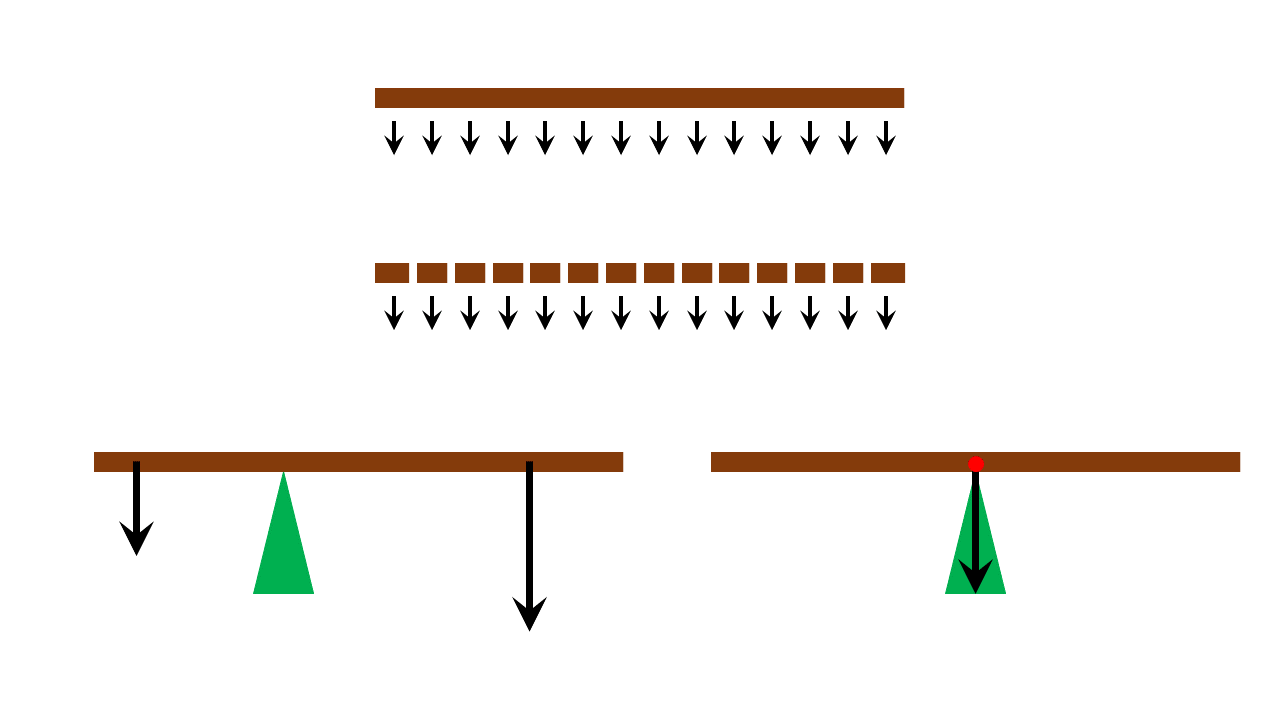
Abbildung 4.1.35: Stab im Gleichgewicht (C)
Der Stab soll überall den gleichen Durchmesser haben. Die Schwerkraft wirkt auf den Stab entlang seiner gesamten Länge. Das ist durch die Pfeile dargestellt. Zerlegt man den Stab gedanklich in kleine Teilstücke, wirkt auf jedes einzelne Teilstück die Schwerkraft. Unterstützt man den Stab an einer beliebigen Stelle, kippt er über die längere Seite nach unten. Wird der Stab jedoch in der Mitte unterstützt, schweben die beiden Enden links und rechts. Die Masse sitzt scheinbar nur in der Mitte direkt über dem Auflagepunkt und die gesamte Gewichtskraft scheint an ihm anzugreifen. Ein solcher Punkt wird als Schwerpunkt bezeichnet.
Jeder Körper besitzt einen Schwerpunkt. Greifen homogene, d.h. ortsunabhängige Kräfte an einem Körper an, verhält sich der Körper so, als ob sämtliche Kräfte an seinem Schwerpunkt (Massenmittelpunkt) angreifen.
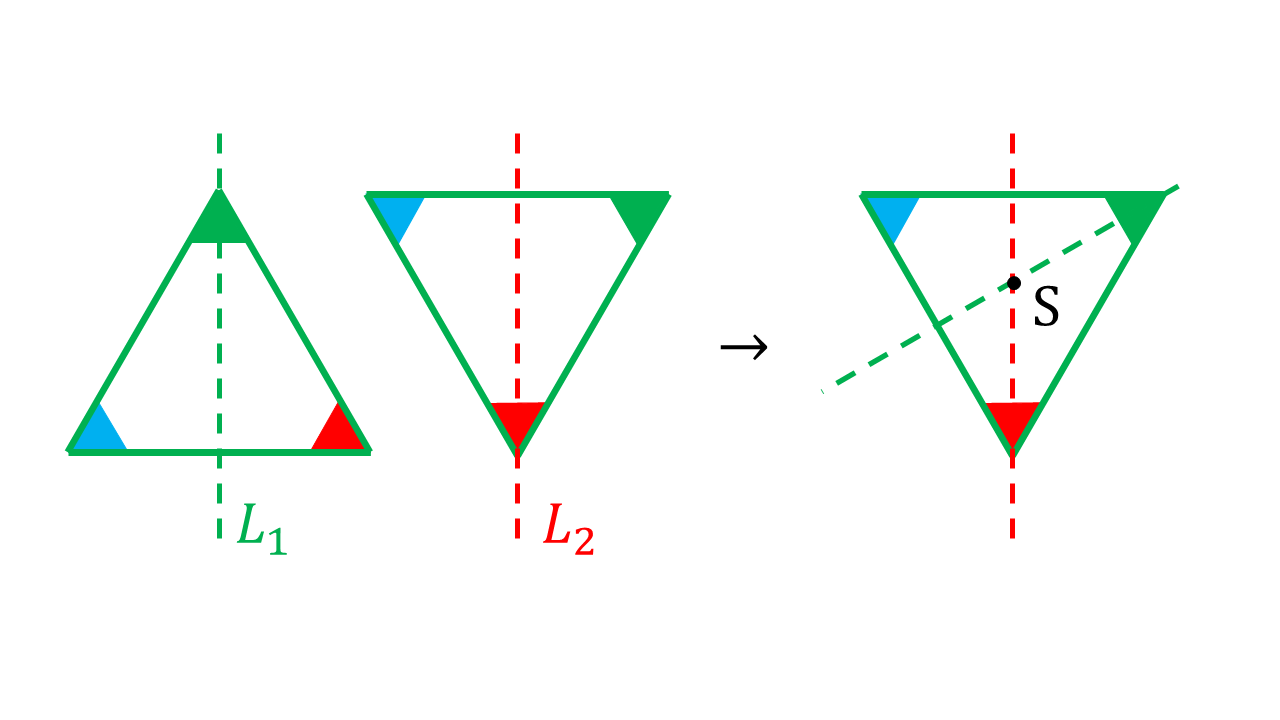
Abbildung 4.1.36: Schwerpunkt eines Dreiecks (C)
Besitzt ein Körper eine homogene Massenverteilung fällt der Massenmittelpunkt mit dem Volumenmittelpunkt zusammen.
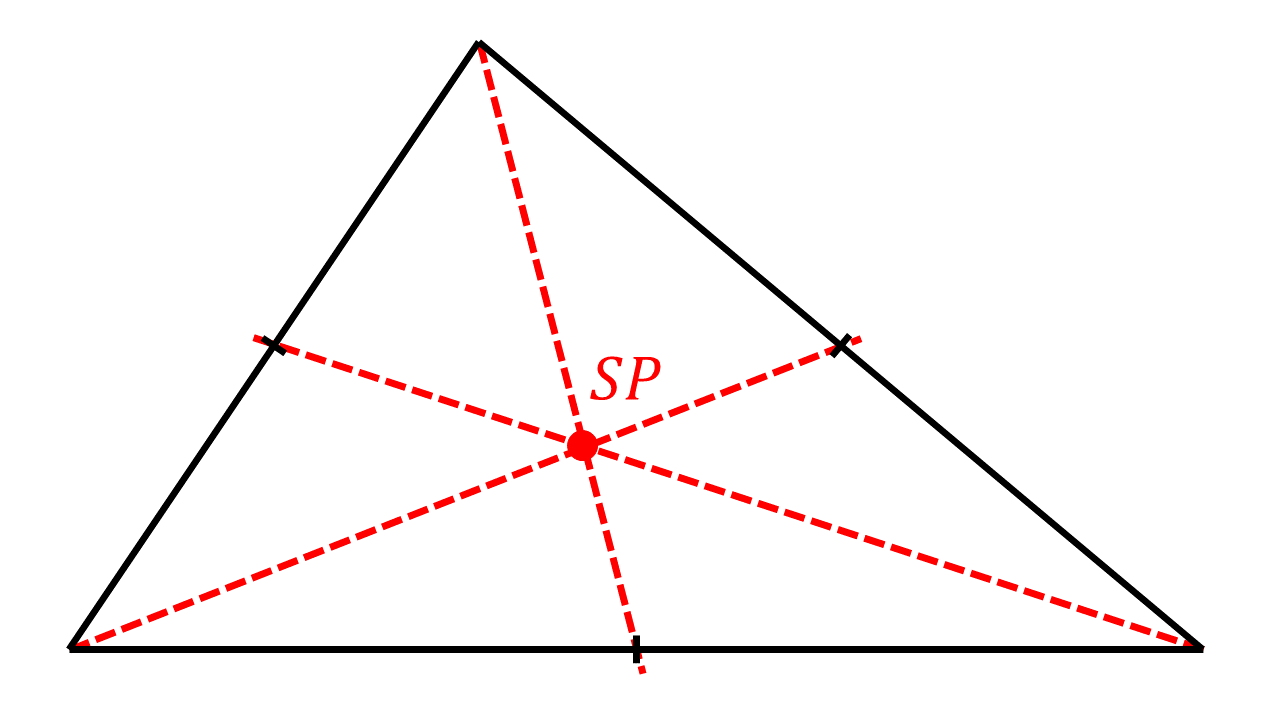
Abbildung 4.1.37: Schwerpunkt eines homogenen Dreiecks (C)
Bei einem homogenen Rechteck liegt der Schwerpunkt im Schnittpunkt der Seitenhalbierenden und bei einem homogenen Kreis im Mittelpunkt:
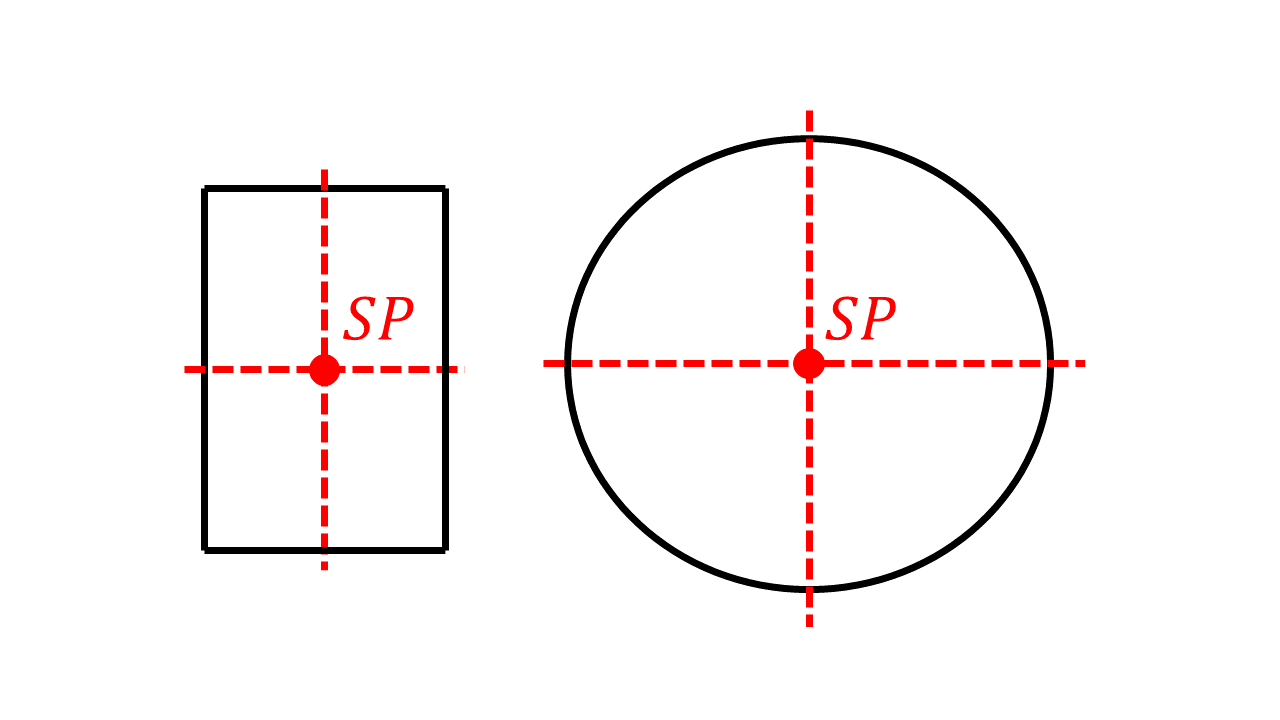
Abbildung 4.1.38: Schwerpunkt eines homogenen Rechtecks und eines Kreises (C)
Der Schwerpunkt eines homogenen Körpers mit dem Volumen kann einfach berechnet werden. Dazu wird der Körper in geeignete Körper zerlegt, von denen die Lage ihres Schwerpunkts bekannt ist. Der Körper kann zum Beispiel in kleine Würfel mit dem Volumen geteilt werden. Der Schwerpunkt eines Würfels befindet sich jeweils in seiner Mitte.
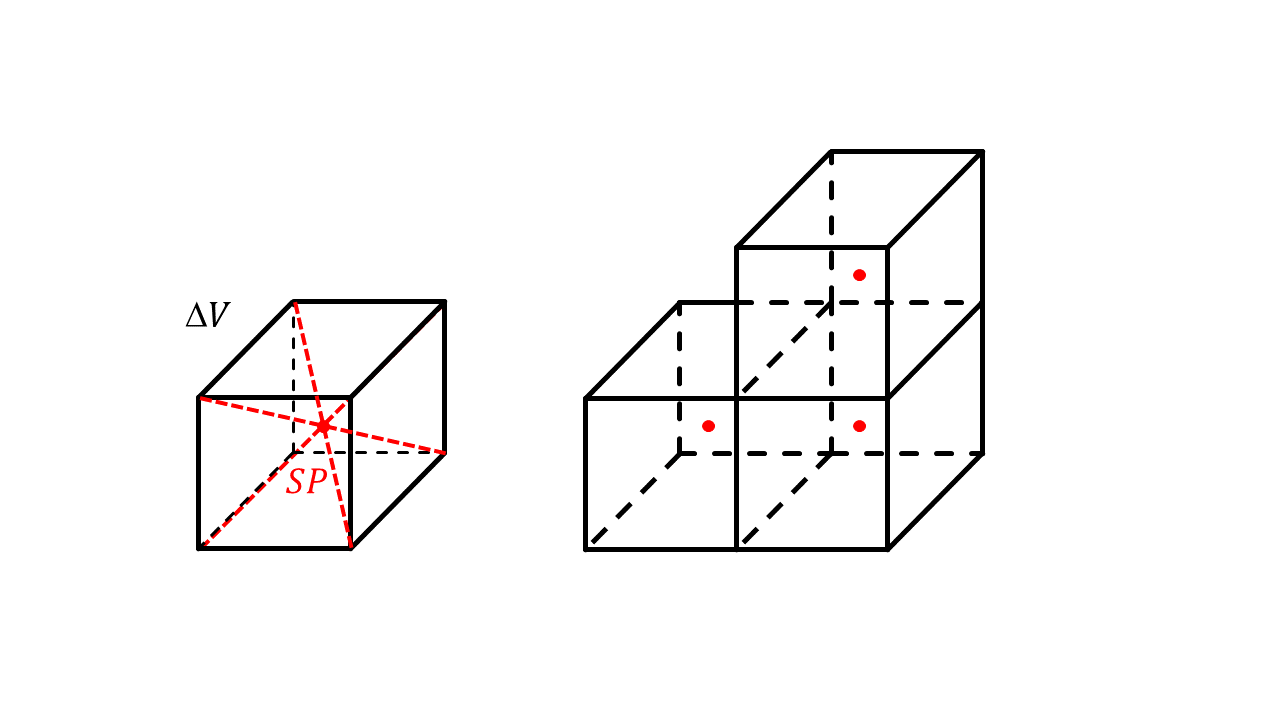
Abbildung 4.1.39: Zerlegung eines Körpers in einzelne Würfel (C)
Für die Koordinaten , und des Schwerpunkts gilt dann:
Dabei sind die , und die Koordinaten der Mittelpunkte der einzelnen Würfel , in die der Körper gedanklich zerlegt wurde.
Beispiel
4.1.12
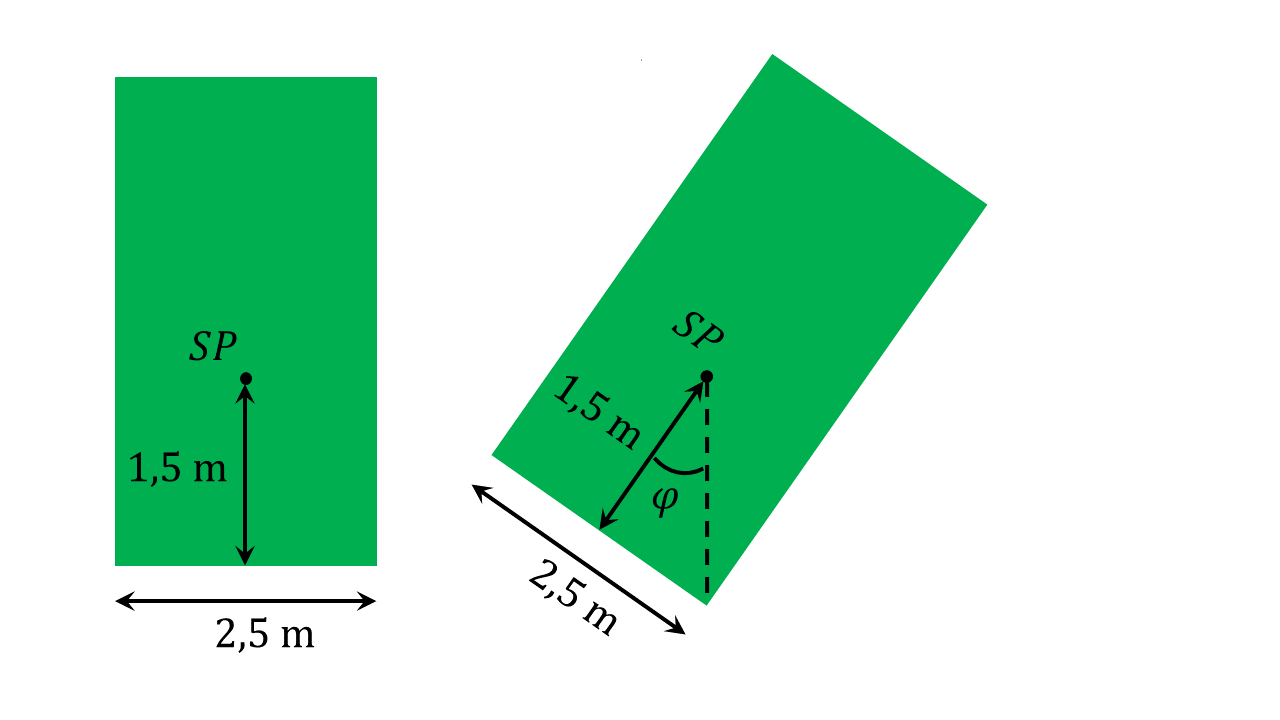
Es soll der Schwerpunkt der gezeigten Fläche berechnet werden.
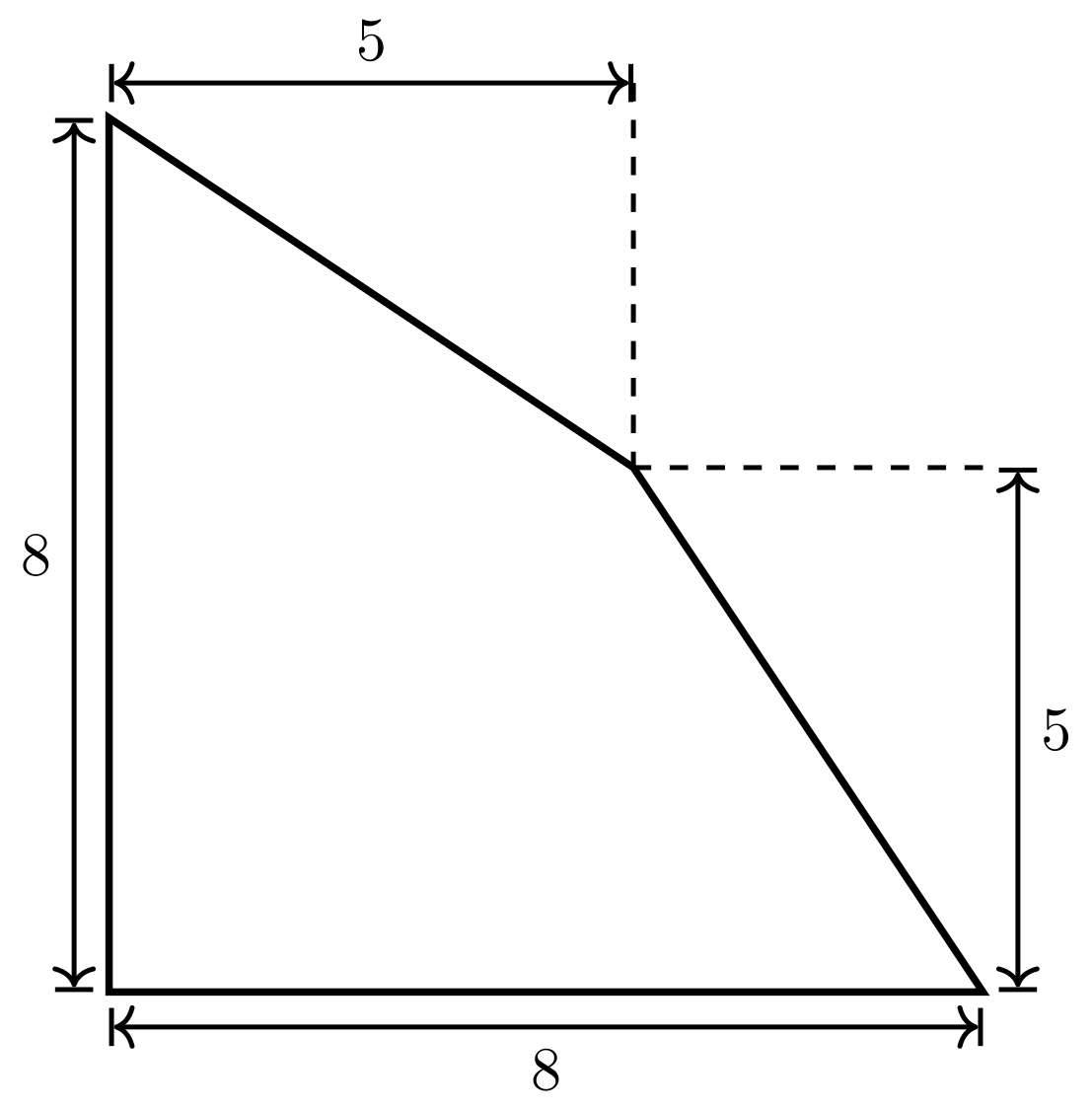
Zur Lösung der Aufgabe wird zuerst ein geeignetes Koordinatensystem gewählt. Hier bietet sich an, den Ursprung des Koordinatensystems in die linke untere Ecke zu legen.
Anschließend wird die Fläche in Teilflächen zerlegt, bei denen eine einfache Bestimmung ihrer Schwerpunkte möglich ist. Eine Zerlegung in ein Quadrat und zwei Dreiecke ist hier gut geeignet.
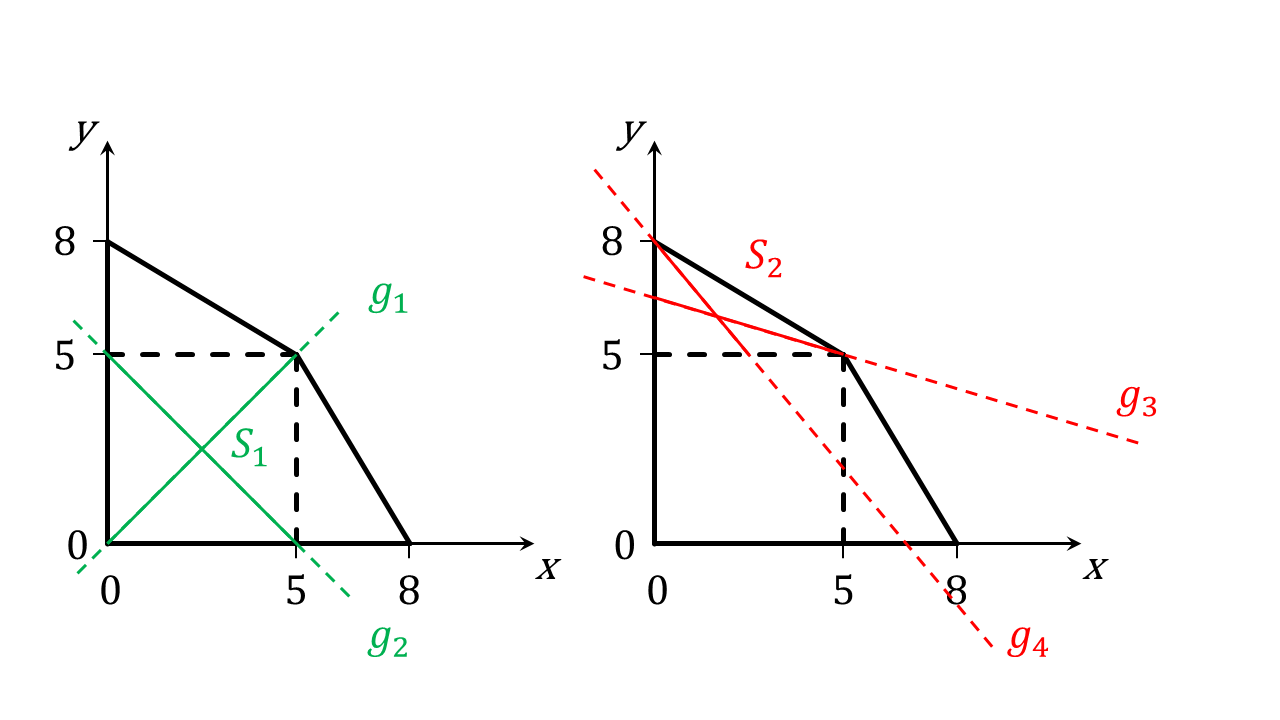
Der Schwerpunkt des Quadrats befindet sich im Schnittpunkt der Geraden und , auf denen die Diagonalen des Quadrats liegen. Dies ist in der Abbildung links gezeigt. Als Koordinaten ergeben sich für den Schwerpunkt des Quadrats:
Der Schwerpunkt des Quadrats befindet also bei .
Zur Berechnung des Schwerpunkts des oberen Dreiecks werden die Gleichungen der Geraden, auf denen die Seitenhalbierenden liegen, bestimmt. Die Gerade geht durch den Punkt , der mittig zwischen den Ecken des Dreiecks der auf der -Achse liegt, und durch den gegenüberliegenden Eckpunkt des Dreiecks . Für die Gerade werden die obere Ecke des Dreiecks und der Mittelpunkt der unteren Seite des Dreiecks verwendet. Für die Geradengleichungen ergeben sich dann:
Durch Gleichsetzen der beiden Geradengleichungen kann die -Koordinate des Schwerpunktes bestimmt werden:
Durch Einsetzen der Koordinate in eine der beiden Geradengleichungen oder ergibt sich:
Der Schwerpunkt des oberen Dreiecks liegt also bei .
Die Figur ist symmetrisch zur ersten Winkelhalbierenden. Damit ergibt sich der Schwerpunkt des zweiten Dreiecks zu .
Für die Rechnung werden die Flächeninhalte des Quadrats und der beiden Dreiecke benötigt. Der Flächeninhalt des Quadrats beträgt . Die Flächeninhalte der beiden Dreiecke sind identisch und ergeben sich zu .
Da hier der Schwerpunkt einer Fläche zu berechnen ist, muss in der Formel anstelle des Volumens die Fläche eingesetzt werden. Für die -Koordinate des Schwerpunkts ergibt sich dann:
Aufgrund der Symmetrie gilt für die -Koordinate . Der Schwerpunkt der gesamten Figur liegt also bei .
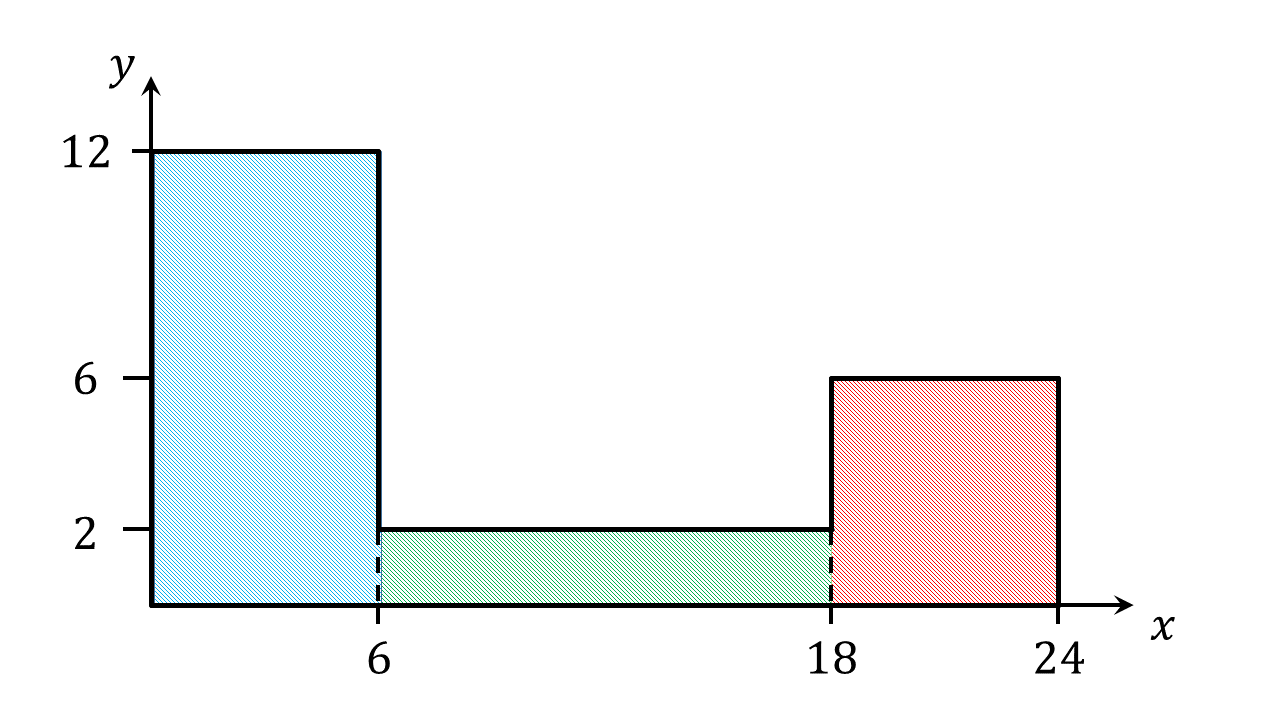
Es soll der Schwerpunkt der gezeigten Fläche berechnet werden.

Abbildung 4.1.40: Zusammengesetzte Fläche (C)
Zur Lösung der Aufgabe wird zuerst ein geeignetes Koordinatensystem gewählt. Hier bietet sich an, den Ursprung des Koordinatensystems in die linke untere Ecke zu legen.
Anschließend wird die Fläche in Teilflächen zerlegt, bei denen eine einfache Bestimmung ihrer Schwerpunkte möglich ist. Eine Zerlegung in ein Quadrat und zwei Dreiecke ist hier gut geeignet.

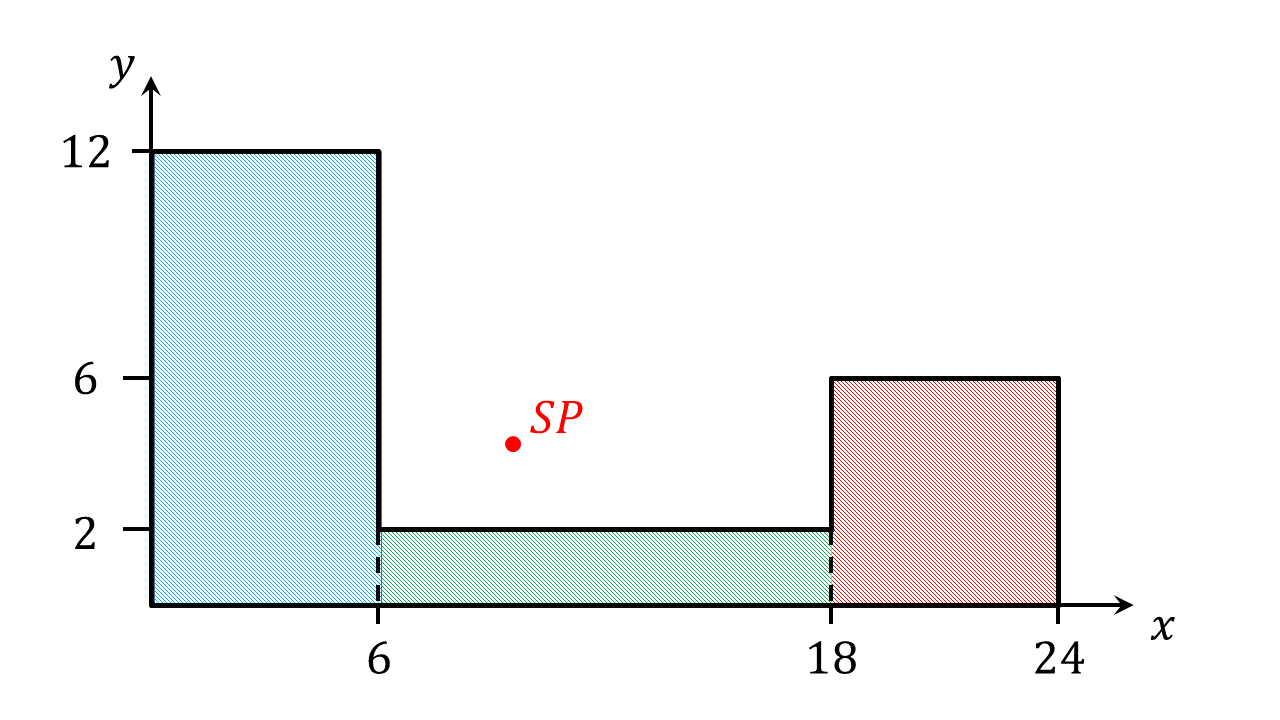
Abbildung 4.1.41: Einzelheiten für die Schwerpunktsberechnung (C)
Der Schwerpunkt des Quadrats befindet sich im Schnittpunkt der Geraden und , auf denen die Diagonalen des Quadrats liegen. Dies ist in der Abbildung links gezeigt. Als Koordinaten ergeben sich für den Schwerpunkt des Quadrats:
Der Schwerpunkt des Quadrats befindet also bei .
Zur Berechnung des Schwerpunkts des oberen Dreiecks werden die Gleichungen der Geraden, auf denen die Seitenhalbierenden liegen, bestimmt. Die Gerade geht durch den Punkt , der mittig zwischen den Ecken des Dreiecks der auf der -Achse liegt, und durch den gegenüberliegenden Eckpunkt des Dreiecks . Für die Gerade werden die obere Ecke des Dreiecks und der Mittelpunkt der unteren Seite des Dreiecks verwendet. Für die Geradengleichungen ergeben sich dann:
Durch Gleichsetzen der beiden Geradengleichungen kann die -Koordinate des Schwerpunktes bestimmt werden:
Durch Einsetzen der Koordinate in eine der beiden Geradengleichungen oder ergibt sich:
Der Schwerpunkt des oberen Dreiecks liegt also bei .
Die Figur ist symmetrisch zur ersten Winkelhalbierenden. Damit ergibt sich der Schwerpunkt des zweiten Dreiecks zu .
Für die Rechnung werden die Flächeninhalte des Quadrats und der beiden Dreiecke benötigt. Der Flächeninhalt des Quadrats beträgt . Die Flächeninhalte der beiden Dreiecke sind identisch und ergeben sich zu .
Da hier der Schwerpunkt einer Fläche zu berechnen ist, muss in der Formel anstelle des Volumens die Fläche eingesetzt werden. Für die -Koordinate des Schwerpunkts ergibt sich dann:
Aufgrund der Symmetrie gilt für die -Koordinate . Der Schwerpunkt der gesamten Figur liegt also bei .
Basiswissen „Gleichgewichtsarten“
Vor Beschreibung der verschiedenen Gleichgewichtsarten sollen zuerst die Gleichgewichtsbedingungen überlegt werden. Wirkt auf einen Körper eine Kraft, kann das zu einer Verschiebung des Körpers in eine Richtung führen.
Ist der Körper drehbar gelagert, kann durch Einwirken einer Kraft ein sogenanntes Drehmoment erzeugt werden. Das soll am Beispiel einer Waage verdeutlicht werden.
In der Abbildung links ist eine Waage mit gleichen Massen auf beiden Tellern gezeigt. Es bewegt sich nichts. Jetzt sollen beide Seiten getrennt betrachtet werden. Durch die Erdanziehung wird der rechte Teller in Richtung Erde gezogen. Der Punkt bewegt sich im Uhrzeigersinn mit konstantem Abstand um den Auflagepunkt nach unten. Für den linken Teller kann diese Überlegung genau so durchgeführt werden, jedoch bewegt sich Punkt entgegen dem Uhrzeigersinn um den Punkt . Durch die Gewichtskraft wird links und rechts ein sogenanntes Drehmoment erzeugt. Die beiden Drehmomente sind betragsmäßig gleich groß, aber entgegengesetzt gerichtet. Sie heben sich im betrachteten Beispiel in ihrer Wirkung auf.
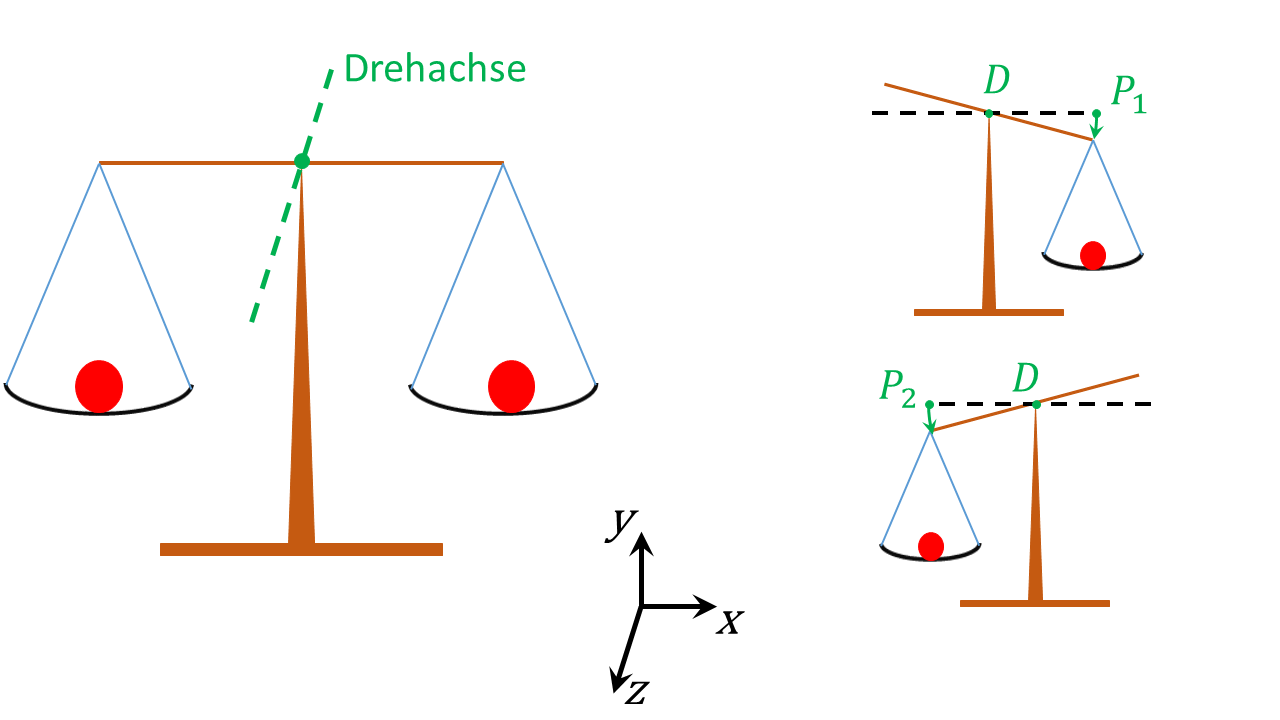
Abbildung 4.1.42: Skizze (C)
Das Drehmoment ist das Produkt aus Kraft und Hebelarm :
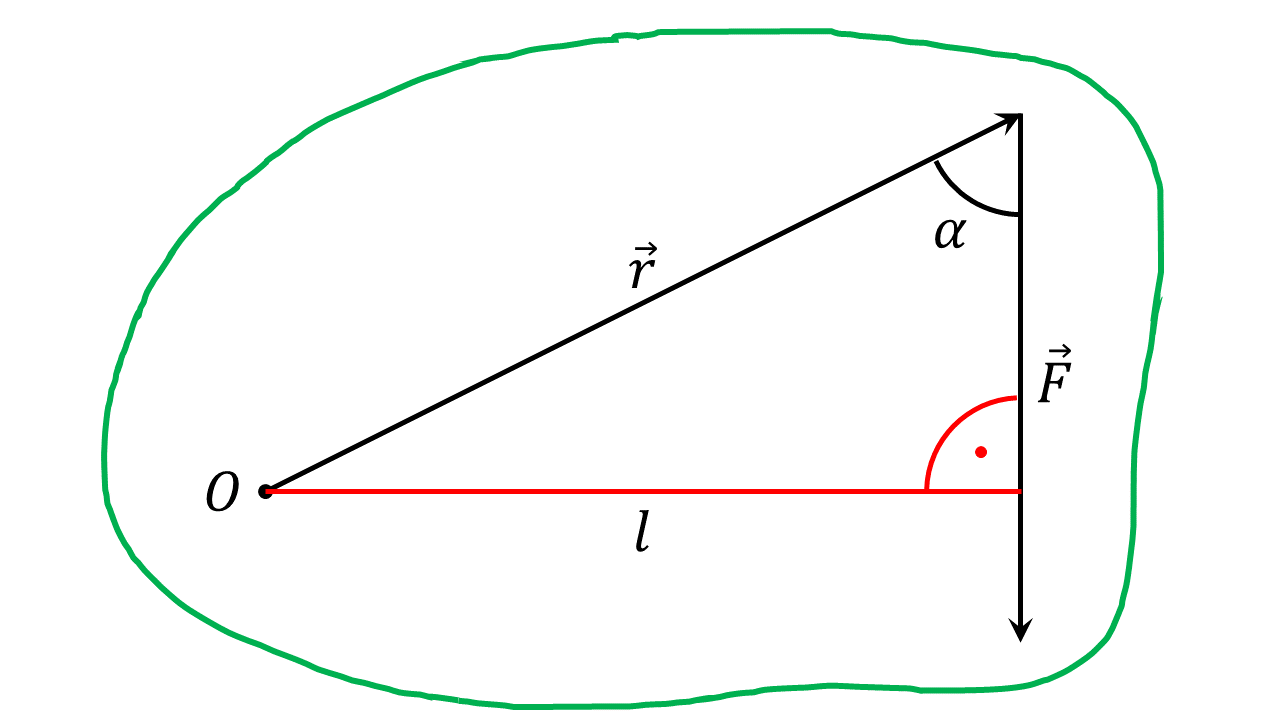
Die Einheit des Drehmoments ist .
Das Drehmoment ist eine vektorielle Größe . Sie steht senkrecht auf der Ebene, die von und aufgespannt wird. Die Richtung kann mit der bestimmt werden.

Abbildung 4.1.43: Drehmoment (C)
Die Einheit des Drehmoments ist .
Das Drehmoment ist eine vektorielle Größe . Sie steht senkrecht auf der Ebene, die von und aufgespannt wird. Die Richtung kann mit der bestimmt werden.
Ein Körper bleibt in Ruhe, wenn die Summe aller an ihm angreifenden Kräfte verschwindet und sich die an ihm angreifenden Drehmomente aufheben.
- Der Körper befindet sich in einer stabilen Gleichgewichtslage. Um den Körper zu bewegen, muss sein Schwerpunkt angehoben werden. Wird der Körper aus dieser Lage ausgelenkt, pendelt er um die stabile Lage und kehrt schließlich wieder zu ihr zurück.
 Abbildung 4.1.44: Stabiles Gleichgewicht (C)
Abbildung 4.1.44: Stabiles Gleichgewicht (C)
- Der Körper befindet sich in einer labilen Gleichgewichtslage. Bei einer Bewegung bewegt sich der Schwerpunkt nach unten. Eine kleine Störung sorgt dafür, dass der Körper sich aus seiner Position bewegt. Der Körper kann nicht in die Ausgangslage zurück.
 Abbildung 4.1.45: Labiles Gleichgewicht (C)
Abbildung 4.1.45: Labiles Gleichgewicht (C)
- Im letzten Fall spricht man von einem indifferenten Gleichgewicht. Bei einer Bewegung bleibt der Schwerpunkt in der gleichen Höhe. Gibt man dem Ball einen Stoß, kommt er wieder zur Ruhe. Die Lage vor und nach dem Stoß kann nicht unterschieden werden.
 Abbildung 4.1.46: Indifferentes Gleichgewicht (C)
Abbildung 4.1.46: Indifferentes Gleichgewicht (C)
Basiswissen „Standfestigkeit“
Ob ein Körper steht oder umfällt, hängt von seiner Form und damit auch von seinem Schwerpunkt ab. Solange der Schwerpunkt des Körper sich oberhalb seiner Standfläche befindet, bleibt er stehen und fällt nicht um. Befindet sich der Schwerpunkt neben der Auflagefläche, kippt der Körper um.
Fällt man das Lot vom Schwerpunkt aus nach unten, bleibt ein Körper nur dann stehen, wenn das Lot die Standfläche des Körpers trifft. Die Standfestigkeit eines Körpers nimmt zu bei:
- einer größeren Standfläche
- einem tiefliegenden Schwerpunkt
- einer größeren Masse des Körpers
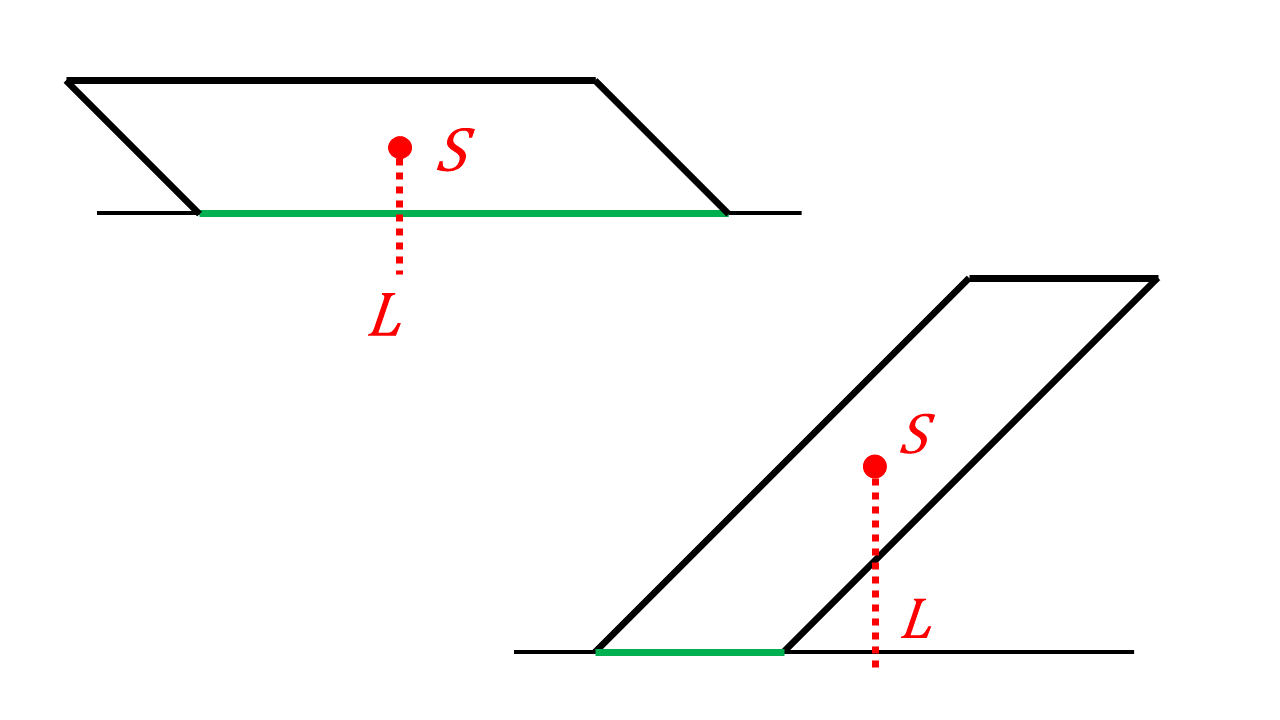
Abbildung 4.1.47: Beispiel für die Standfestigkeit eines Körpers (C)
Wenn in den folgenden Aufgabentexten nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie
Aufgabe 4.1.13
Ein Würfel, der auf seiner Kante steht, befindet sich in einem Gleichgewicht.
Ein Würfel, der auf seiner Seite steht, befindet sich in einem Gleichgewicht.
Ein Würfel, der auf seiner Kante steht, befindet sich in einem Gleichgewicht.
Ein Würfel, der auf seiner Seite steht, befindet sich in einem Gleichgewicht.
Aufgabe 4.1.14
Zum Studienbeginn ziehen Sie von zu Hause in Ihre neue Wohnung um. Sie haben etliche Kisten gepackt, die unterschiedlich schwer sind. Um alles auf einmal mitnehmen zu können, haben Sie den Dachgepäckträger auf Ihr Auto montiert.
Wie verstauen Sie im Idealfall das Gepäck, um ihre Standfestigkeit für die Fahrt zu erhöhen?

Zum Studienbeginn ziehen Sie von zu Hause in Ihre neue Wohnung um. Sie haben etliche Kisten gepackt, die unterschiedlich schwer sind. Um alles auf einmal mitnehmen zu können, haben Sie den Dachgepäckträger auf Ihr Auto montiert.
Wie verstauen Sie im Idealfall das Gepäck, um ihre Standfestigkeit für die Fahrt zu erhöhen?

Abbildung 4.1.48: Skizze (C)
| Die schweren Kisten auf das Dach und die leichten Kisten in Kofferraum und Fahrerkabine. | |
| Die schweren Kisten möglichst weit unten und die leichten Kisten oben. | |
| Es ist völlig egal wie das Auto gepackt wird, Hauptsache alles passt rein. | |
| Ohne weitere Angaben kann dazu nichts gesagt werden. | |
| Es sollte möglichst alles auf das Dach gepackt werden. |
Aufgabe 4.1.15
Mäxchen spielt mit seinen Bauklötzen. Welche der in der Abbildung gezeigten Türme stürzen nicht ein?
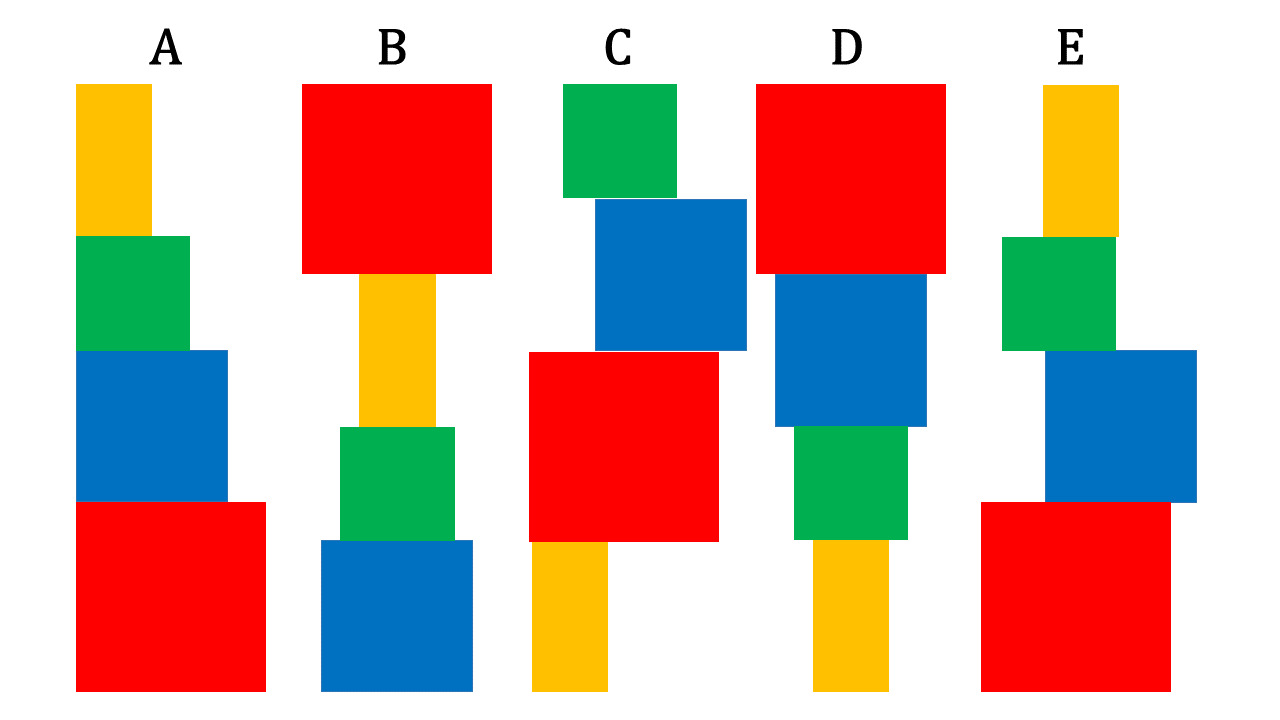
Mäxchen spielt mit seinen Bauklötzen. Welche der in der Abbildung gezeigten Türme stürzen nicht ein?
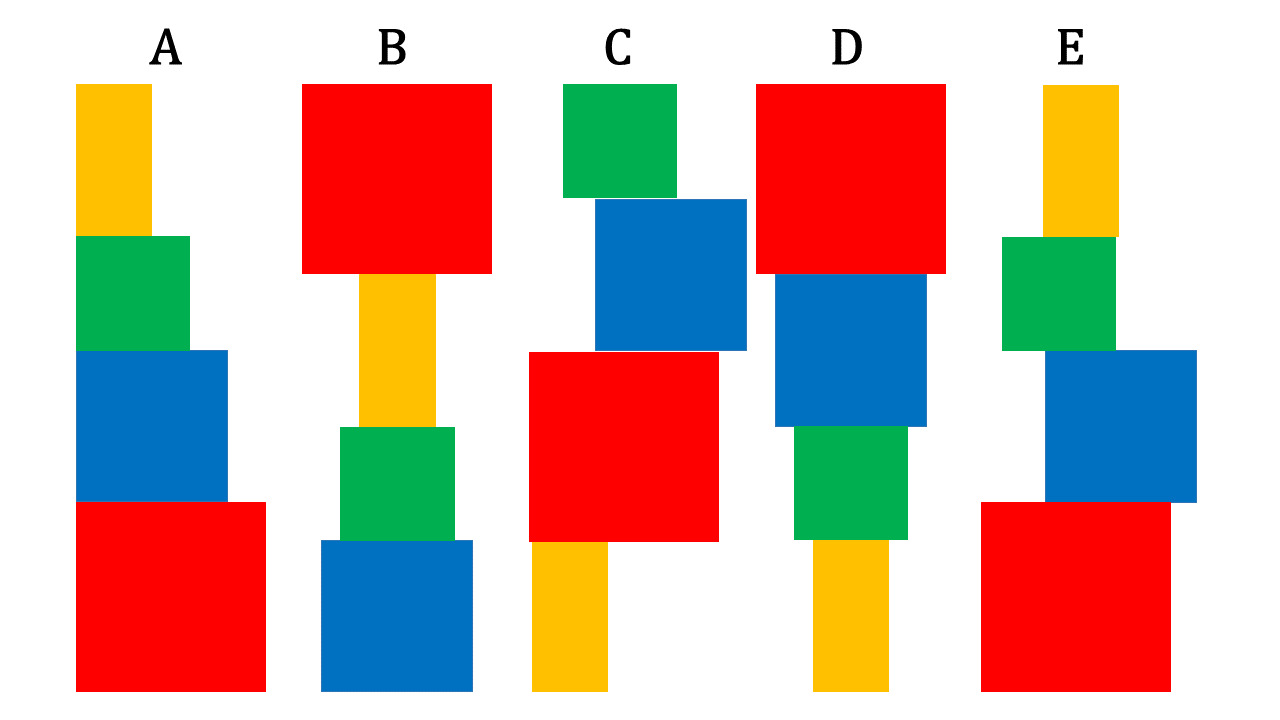
Abbildung 4.1.49: Skizze (C)
Aufgabe 4.1.16
Ein Reisebus hat eine Höhe von und ist breit. Sein Schwerpunkt befindet sich in einer Höhe von . Um welchen Winkel kann der Bus maximal gekippt werden ohne umzufallen?
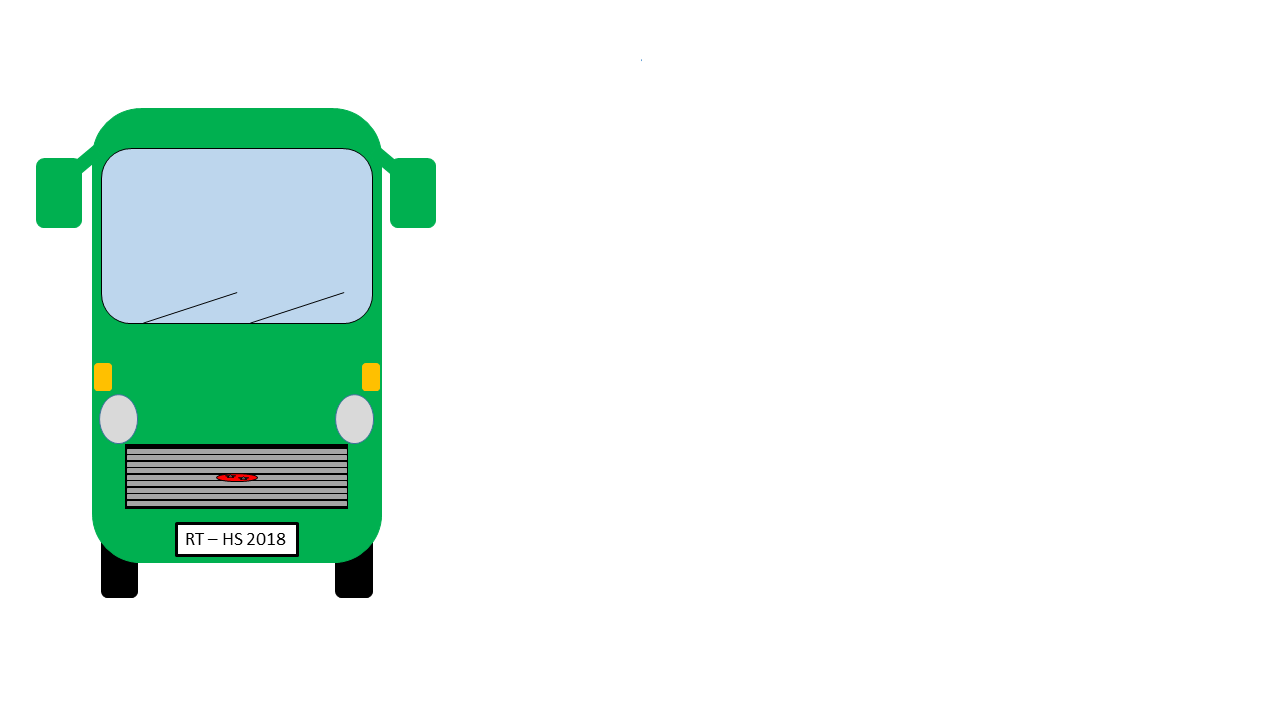
Ein Reisebus hat eine Höhe von und ist breit. Sein Schwerpunkt befindet sich in einer Höhe von . Um welchen Winkel kann der Bus maximal gekippt werden ohne umzufallen?

Abbildung 4.1.50: Skizze (C)
Aufgabe 4.1.17
Drei Punkte mit jeweils der gleichen Masse befinden sich auf den Spitzen eines Dreiecks angeordnet, wie in der Abbildung skizziert. Berechnen Sie die Koordinaten des Massenmittelpunktes.
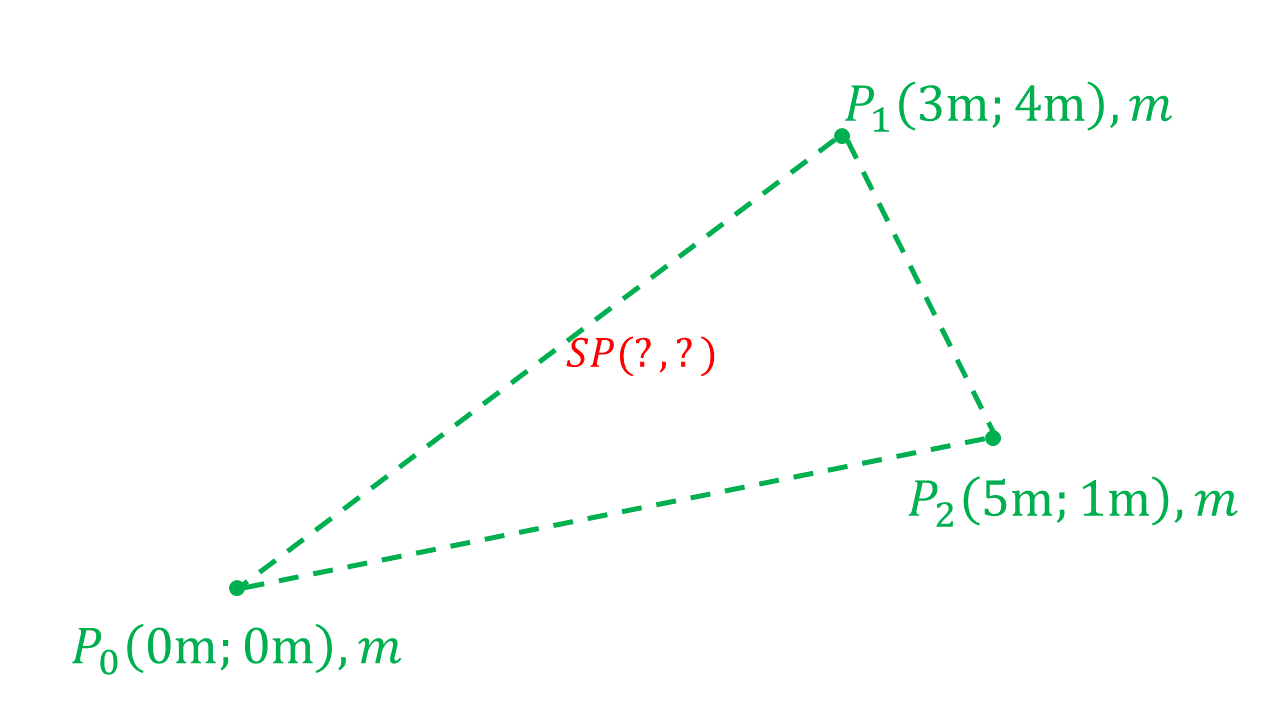
Geben Sie das Ergebnis auf zwei Stellen an:


Drei Punkte mit jeweils der gleichen Masse befinden sich auf den Spitzen eines Dreiecks angeordnet, wie in der Abbildung skizziert. Berechnen Sie die Koordinaten des Massenmittelpunktes.

Abbildung 4.1.52: Skizze (C)
Geben Sie das Ergebnis auf zwei Stellen an:
Aufgabe 4.1.18
Berechnen Sie die - und die -Koordinate des Schwerpunkts der in der Abbildung gezeigten Figur.
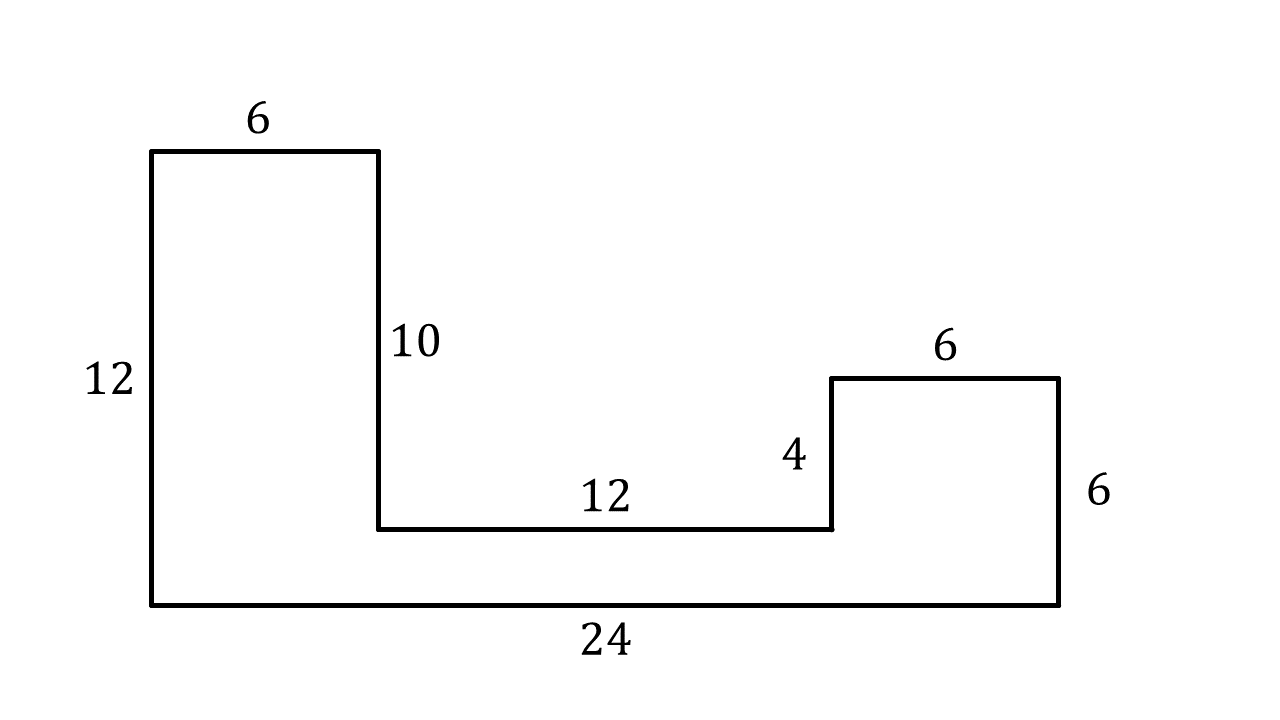
Zerlegen Sie dazu die Figur in geeignete Teilflächen. Verwenden Sie als Koordinatenursprung die linke untere Ecke der Figur. Die -Achse soll horizontal und die -Achse vertikal verlaufen.
Geben Sie das Ergebnis auf zwei Stellen nach dem Komma an:


Berechnen Sie die - und die -Koordinate des Schwerpunkts der in der Abbildung gezeigten Figur.

Abbildung 4.1.53: Skizze (C)
Zerlegen Sie dazu die Figur in geeignete Teilflächen. Verwenden Sie als Koordinatenursprung die linke untere Ecke der Figur. Die -Achse soll horizontal und die -Achse vertikal verlaufen.
Geben Sie das Ergebnis auf zwei Stellen nach dem Komma an:
Resultierende Kraft (!)
Das Video zu Resultierende Kraft wird überarbeitet.
Definition der resultierenden Kraft.
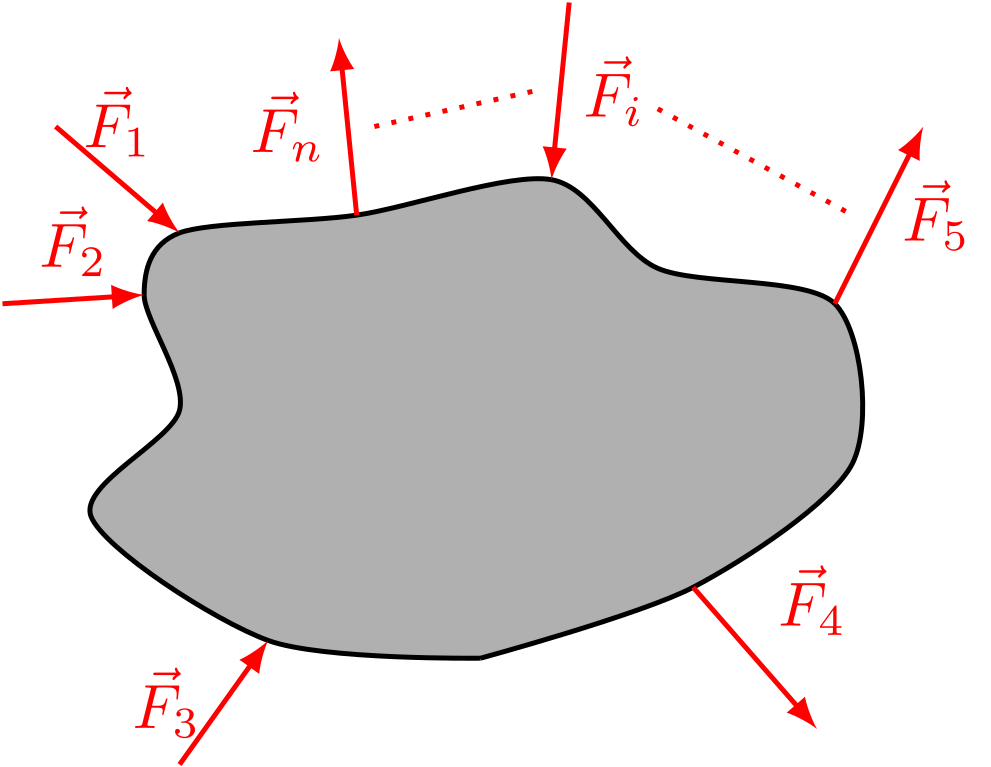
Wirkt eine Gruppe aus Kräften auf einen Körper, dann kann die Gesamtwirkung aller Kräfte (auf seinen „Massenmittelpunkt“) durch eine resultierende Kraft beschrieben werden, und es gilt:
mit als resultierender Gesamtkraft.

Abbildung 4.1.56: Kräfte wirken auf einen Körper (C)
Wirkt eine Gruppe aus Kräften auf einen Körper, dann kann die Gesamtwirkung aller Kräfte (auf seinen „Massenmittelpunkt“) durch eine resultierende Kraft beschrieben werden, und es gilt:
mit als resultierender Gesamtkraft.
Kräftegleichgewicht (!)
Das Video zu Kräftegleichgewicht wird überarbeitet.
Video 7: Fehlende Kraft für Gleichgewicht, Betrag (C)
.
Video 8: Fehlende Kraft für Gleichgewicht, Winkel (C)
.
Beispiel
4.1.19
Drei Kinder ziehen jeweils in radialer Richtung mit den Kräften , und an einem Ring (siehe Skizze). Gesucht ist die Kraft so, dass der Ring im Gleichgewicht ist. Dazu wird zunächst in kartesischen Komponenten bestimmt. Danach können der Betrag von sowie der Winkel, den die Kraft mit der positiven -Achse einschließt, angegeben werden.
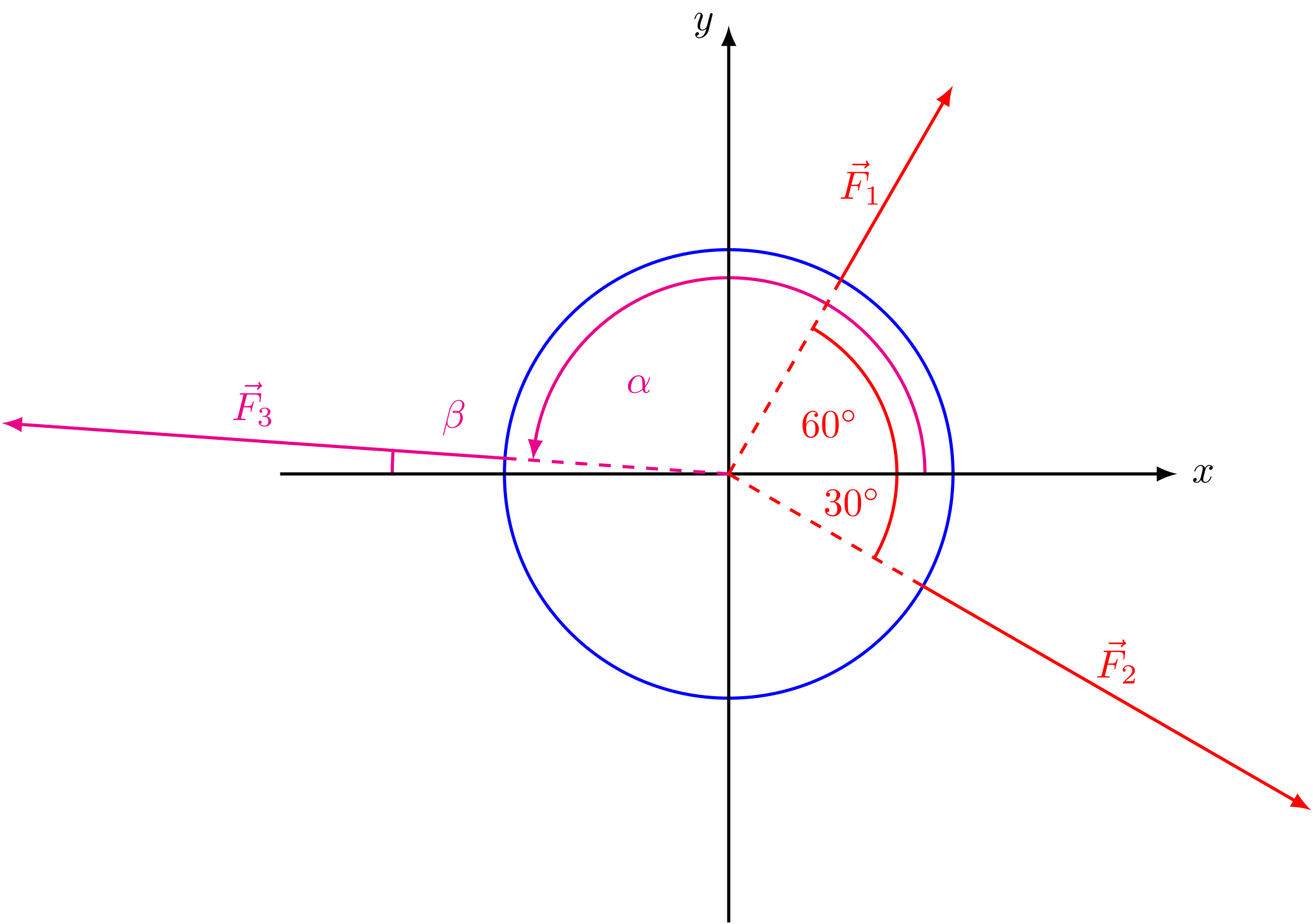
Für das Kräftegleichgewicht muss oder
gelten.
Mit und erhalten wir in kartesischen Komponenten (vergleiche dazu Seite 3.1.2)
Die Berechnung des Betrages mit den gerundeten Komponenten liefert
Der mit der positiven -Achse eingeschlossene Winkel wird bestimmt, indem von der mit der negativen -Achse eingeschlossene Winkel , der aus den Beträgen der Komponenten berechnet werden kann, abgezogen wird:
(siehe Skizze).
Drei Kinder ziehen jeweils in radialer Richtung mit den Kräften , und an einem Ring (siehe Skizze). Gesucht ist die Kraft so, dass der Ring im Gleichgewicht ist. Dazu wird zunächst in kartesischen Komponenten bestimmt. Danach können der Betrag von sowie der Winkel, den die Kraft mit der positiven -Achse einschließt, angegeben werden.

Abbildung 4.1.57: Auf den Ring wirkende Kräfte (C)
Für das Kräftegleichgewicht muss oder
gelten.
Mit und erhalten wir in kartesischen Komponenten (vergleiche dazu Seite 3.1.2)
Die Berechnung des Betrages mit den gerundeten Komponenten liefert
Der mit der positiven -Achse eingeschlossene Winkel wird bestimmt, indem von der mit der negativen -Achse eingeschlossene Winkel , der aus den Beträgen der Komponenten berechnet werden kann, abgezogen wird:
(siehe Skizze).
Normalkraft (!)
Steht ein Objekt auf dem Boden, so ändert sich sein Bewegungszustand nicht. Bei einem Objekt auf der Erdoberfläche wirkt jedoch die Gravitationskraft bzw. die Gewichtskraft. Zur Veranschaulichung betrachten wir was passiert wenn sich eine Person auf eine Matratze stellt.
Die Matratze wird sich auf Grund der Gewichtskraft verformen.
Betrachtet man die Matratze wird es auf Grund der Verformung eine Kraft entgegen der Auslenkung geben. Je mehr die Matratze eingedrückt ist, desto größer wird die Gegenkraft sein. Ist diese Gegenkraft betragsmäßig so groß wie die Gewichtskraft, ist das Kräftegleichgewicht erreicht. Man erkennt das auf den Körper keine effektive Kraft mehr wirkt.
Diese Kraft ist eine sogenannte Reaktions- bzw. Zwangskraft, die das Eindringen in die Oberfläche verhindert. Sie wird im Fall einer harten Oberfläche als Normalkraft bezeichnet.
Die Normalkraft auf einer horizontalen Ebene kompensiert immer gerade die Gewichtskraft. Damit gilt in diesem Fall
und
Beispiel
4.1.20
Stellt man einen Holzklotz auf einen Steintisch, so wird auch der Tisch verformt. Diese geometrische Verformung ist dabei natürlich vernachlässigbar, die auftretende Normalkraft allerdings nicht.
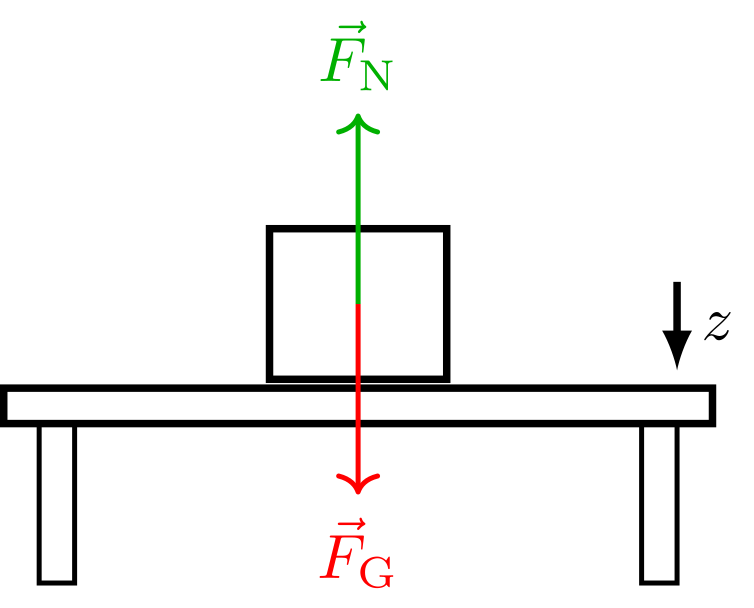
Anhand dieses Beispiels wird die hier der Wert der Normalkraft nochmals mathematisch hergeleitet. Dabei zeigt die positive -Achse wie in der Skizze angedeutet nach unten.
Aus Seite 4.1.1 wissen wir, dass die Kraft proportional zur Beschleunigung ist,
Hier ist nur die -Komponente von Bedeutung. Damit ergibt sich
Befindet sich der Körper in Ruhe und verbleibt auch in Ruhe dann ist . Damit ergibt sich
Stellt man einen Holzklotz auf einen Steintisch, so wird auch der Tisch verformt. Diese geometrische Verformung ist dabei natürlich vernachlässigbar, die auftretende Normalkraft allerdings nicht.

Abbildung 4.1.61: Holzklotz auf Steintisch (C)
Hier ist nur die -Komponente von Bedeutung. Damit ergibt sich
Befindet sich der Körper in Ruhe und verbleibt auch in Ruhe dann ist . Damit ergibt sich
Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie .
Falls nicht anders angegeben, verwenden Sie