8.2.6 Stehende Wellen
Video 11: Stehende Wellen (C)
.
Video 12: Stehende Schallwellen (C)
.
Stehende Wellen (*)
Unter einer „stehenden Welle“ versteht man eine ortsfeste Welle mit Schwingungsknoten (Auslenkung immer Null) und -bäuchen (Auslenkung wechselt zwischen ).
Entstehung: Zwei gegenläufige Wellen mit gleicher Frequenz und Amplitude interferieren. Ursache ist entweder die Reflexion an einer Wand oder zwei Quellen mit entgegengesetzter Abstrahlung.
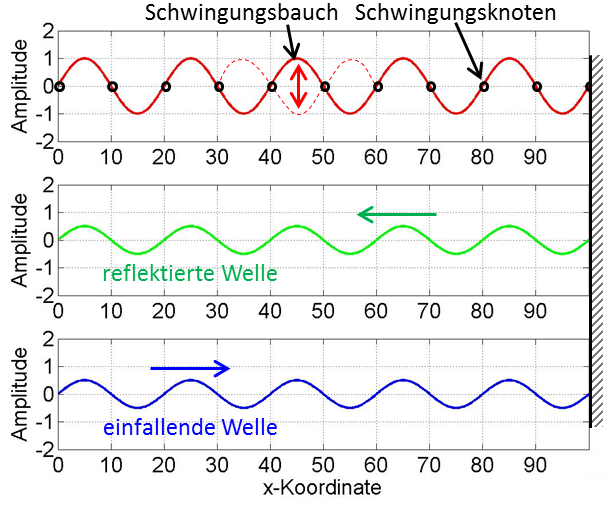
Abbildung 8.2.278: Überlagerung von einfallender und reflektierter Welle zu stehender Welle (C)
Rechnerische Interferenz zwei gegenläufiger Wellen gleicher Frequenz und Amplitude:
| Wellenfunktion 1 (nach rechts) | |
| Wellenfunktion 2 (nach links) | |
| nach Interferenz | |
| Additionstheorem und | |
| Schwingungsknoten | für |
| Schwingungsbäuche | für |
Vorkommen von stehenden Wellen
Bei mechanischen Wellen: Ein Medium wird an einer Stelle zu Schwingungen angeregt. Es breiten sich Wellen aus, die an den Rändern des Mediums hin und her reflektiert werden und sich zu stehenden Wellen überlagern.
| Einmalige (kurze) Anregung: | es bilden sich stehende Wellen aus, deren Frequenzen von den Abmessungen und Eigenschaften des Mediums abhängt (sogenannte Eigenfrequenzen). |
| Periodische Anregung: | es bilden sich nur dann stehende Wellen aus, wenn die Anregungsfrequenz mit einer der Eigenfrequenzen übereinstimmt (Resonanz). |
- Saite eines Musikinstrumentes (1-dim.)
- Luftsäule in einem dünnen Rohr (1-dim., s.u.)
- Technische Membranen, Plattenschwingungen
- Verstärkung von Licht zwischen 2 parallelen Spiegeln
Stehende Wellen und Eigenschwingungen
Die stehenden Wellen, die sich in einem abgegrenzten Medium (Resonator) durch Reflexion an den Rändern ausbilden, nennt man „Eigenschwingungen“ mit jeweils einer „Eigenfrequenz“. Die tiefste mögliche Eigenfrequenz heißt „Grundfrequenz“. Ihr Betrag richtet sich nach den Abmessungen des Resonators und den elastischen Eigenschaften des schwingenden Mediums. Alle höheren Eigenfrequenzen (auch oft als „harmonische Obertöne“ bezeichnet) sind ein ganzzahliges Vielfaches der Grundfrequenz.
Die stehenden Wellen, die sich in einem abgegrenzten Medium (Resonator) durch Reflexion an den Rändern ausbilden, nennt man „Eigenschwingungen“ mit jeweils einer „Eigenfrequenz“. Die tiefste mögliche Eigenfrequenz heißt „Grundfrequenz“. Ihr Betrag richtet sich nach den Abmessungen des Resonators und den elastischen Eigenschaften des schwingenden Mediums. Alle höheren Eigenfrequenzen (auch oft als „harmonische Obertöne“ bezeichnet) sind ein ganzzahliges Vielfaches der Grundfrequenz.
Wenn eine Saite zu Schwingungen angeregt wird, können sich stehende Wellen ausbilden, deren Form von der Frequenz und den Randbedingungen abhängt. Wenn die Saite an beiden Enden fest eingespannt ist, tritt bei der Reflexion einer Welle immer ein Phasensprung von und ein Schwingungsknoten auf, da sich die Saite nicht bewegen kann. An einem offenen Ende wird eine Welle ohne Phasensprung reflektiert.
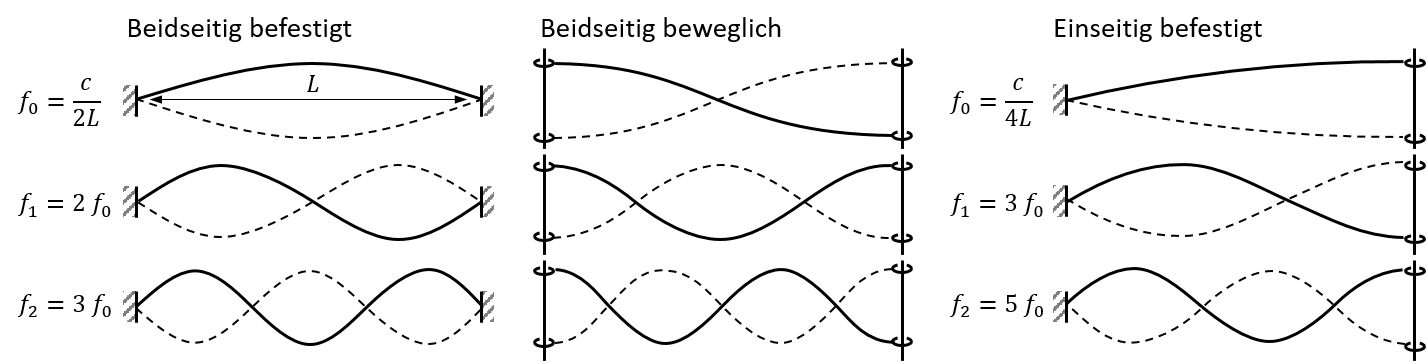
Abbildung 8.2.279: Stehende Wellen einer Saite für verschiedene Randbedingungen (C)
Bei der Grundfrequenz läuft ausgehend vom linken Ende regelmäßig nach Ablauf der Periodendauer eine Erregerwelle los. Bis zur Vollendung einer ganzen Periode der stehenden Welle legt die Erregerwelle bei beidseitiger Einspannung die Distanz zwischen den Enden 2 Mal zurück, d.h. sie wird 1 Mal an der rechten Seite reflektiert (vgl. Grafik unten links). Bei einseitiger Einspannung durchläuft die Erregerwelle die Distanz insgesamt 4 Mal und wird 3 Mal reflektiert (vgl. Grafik rechts):
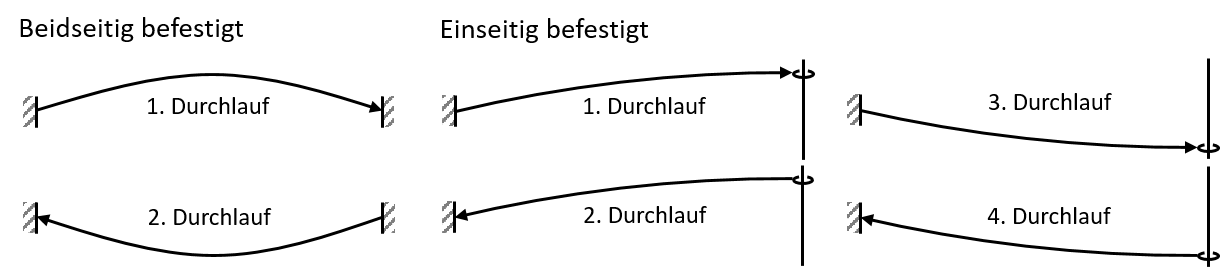
Abbildung 8.2.280: Durchlauf der Erregerwelle (C)
Akustik: 1-dim. stehende Longitudinalwellen in einem dünnen Rohr
Je nach Gestaltung der Randbedingungen bzw. Rohrenden (offen oder geschlossen), tritt bei der Reflexion ein Phasensprung um auf (Schwingungsknoten) oder nicht (Schwingungsbauch). Dargestellt sind die ersten drei stehenden Schalldruckwellen in einem Rohr, dessen Luftsäule zu longitudinalen Schwingungen angeregt wird.
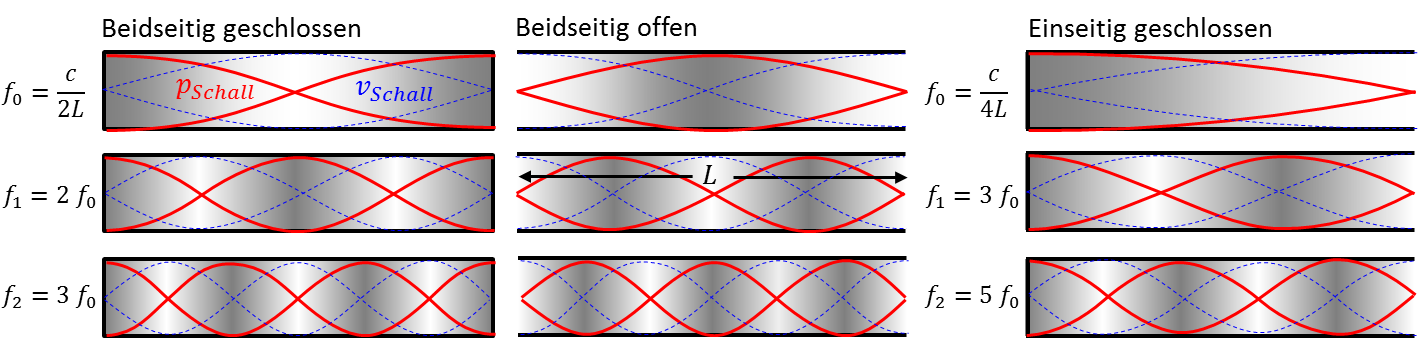
Abbildung 8.2.281: Stehende Schalldruckwellen in einem Rohr für verschiedene Randbedingungen (C)
Beispiel
8.2.14
Der Auspuff Ihres Autos (mit einem 4-Zylinder-4-Takt-Motor) ist leider komplett abgefallen und Sie ersetzen ihn notdürftig durch ein Rohr mit der Länge . Bei welchen Drehzahlen im Bereich bis erwarten Sie ein besonders lautes Motorgeräusch?
Gegeben:
Der Auspuff Ihres Autos (mit einem 4-Zylinder-4-Takt-Motor) ist leider komplett abgefallen und Sie ersetzen ihn notdürftig durch ein Rohr mit der Länge . Bei welchen Drehzahlen im Bereich bis erwarten Sie ein besonders lautes Motorgeräusch?
Gegeben:

