2. Mechanik
  3. Gleichförmige und beschleunigte Bewegungen
  4. Zweidimensionale Bewegungen (!),(*),(+)

4.2.3 Zweidimensionale Bewegungen





 

Basiswissen „Waagerechter Wurf“


Bei einem waagerechten Wurf wird ein Körper horizontal geworfen. Der Körper bewegt sich in horizontaler Richtung mit einer konstanten Geschwindigkeit fort. Gleichzeitig wird er durch die Gravitation der Erde angezogen und dabei vertikal beschleunigt. Es überlagern sich also eine gleichförmige Bewegung und eine gleichförmig beschleunigte Bewegung in zwei orthogonalen Richtungen. Die Behandlung eines solchen Problems scheint auf den ersten Blick schwierig, jedoch können die Bewegungen in beide Richtungen unabhängig voneinander behandelt werden. Für die Beschreibung dieser Bewegungen gelten die schon bekannten Formeln und Beziehungen.
Beim waagerechten Wurf gilt – wenn die y-Achse in Richtung Erdmittelpunkt zeigt – für die Geschwindigkeitskomponenten in x- und in y-Richtung:

vx = v0     und     vy =g·t .

Für den zurückgelegten Weg ergibt sich:

sx = v0 ·t    und     sy = 1 2 ·g· t2  .

Sowohl die Geschwindigkeit als auch der zurückgelegte Weg in x- und y-Richtung können als Vektoren dargestellt werden:
 
v → =( vx vy )=( v0 g·t ) ,    s → =( sx sy )=( v0 ·t 1 2 ·g· t2 ) ,
 
wobei v0 die Startgeschwindigkeit ist.
In der Abbildung ist schematisch ein waagerechter Wurf dargestellt. Zum Startzeitpunkt erhält der Ball die konstante Geschwindigkeit v0 in x-Richtung. Ab diesem Zeitpunkt wird der Ball nach den Gesetzen des freien Falls nach unten beschleunigt. Der Ball bewegt sich genau so lange in x-Richtung weiter, wie er fällt. Die Flugzeit ist für die beiden Bewegungen identisch.


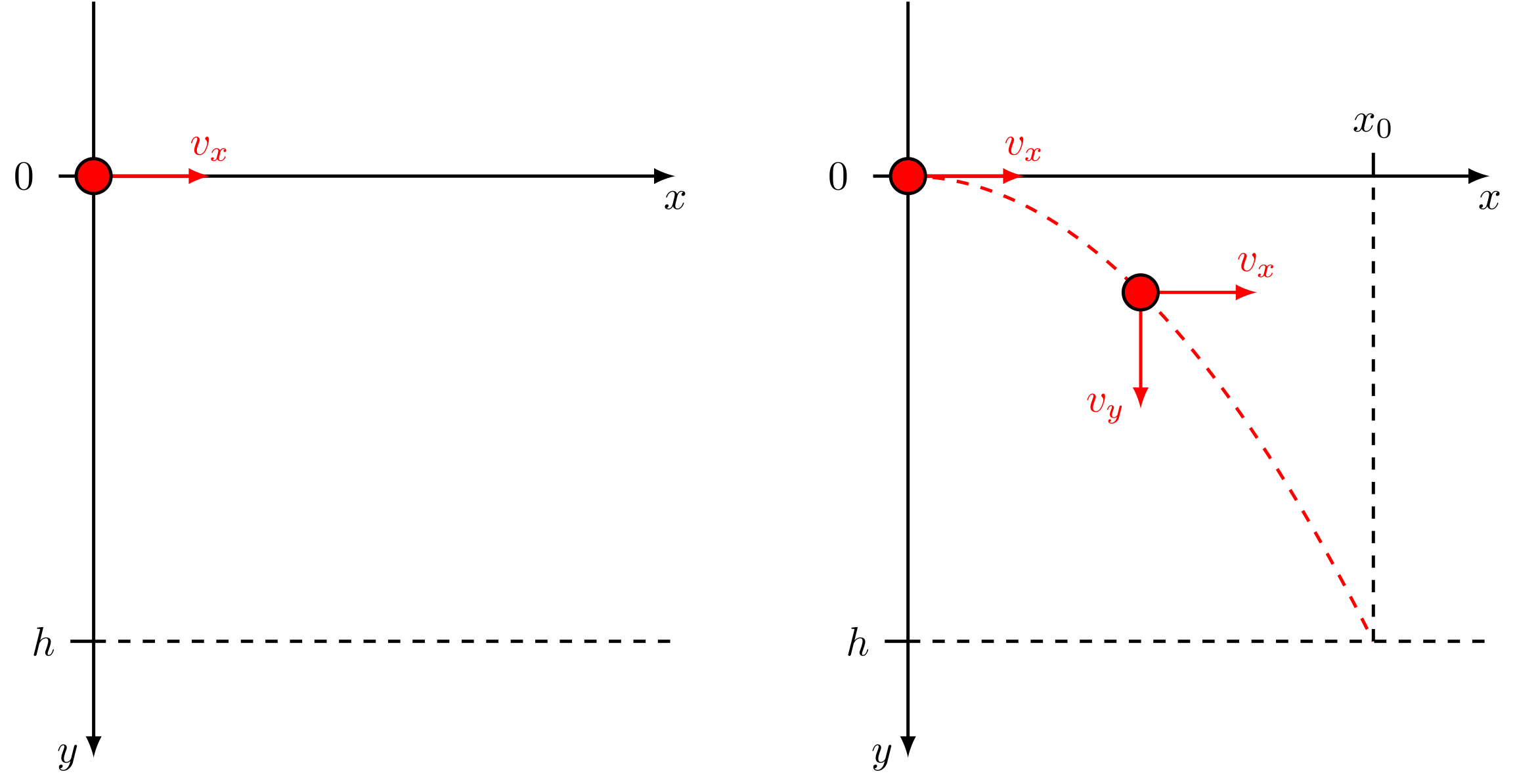
./_3136A1EC_4x.png
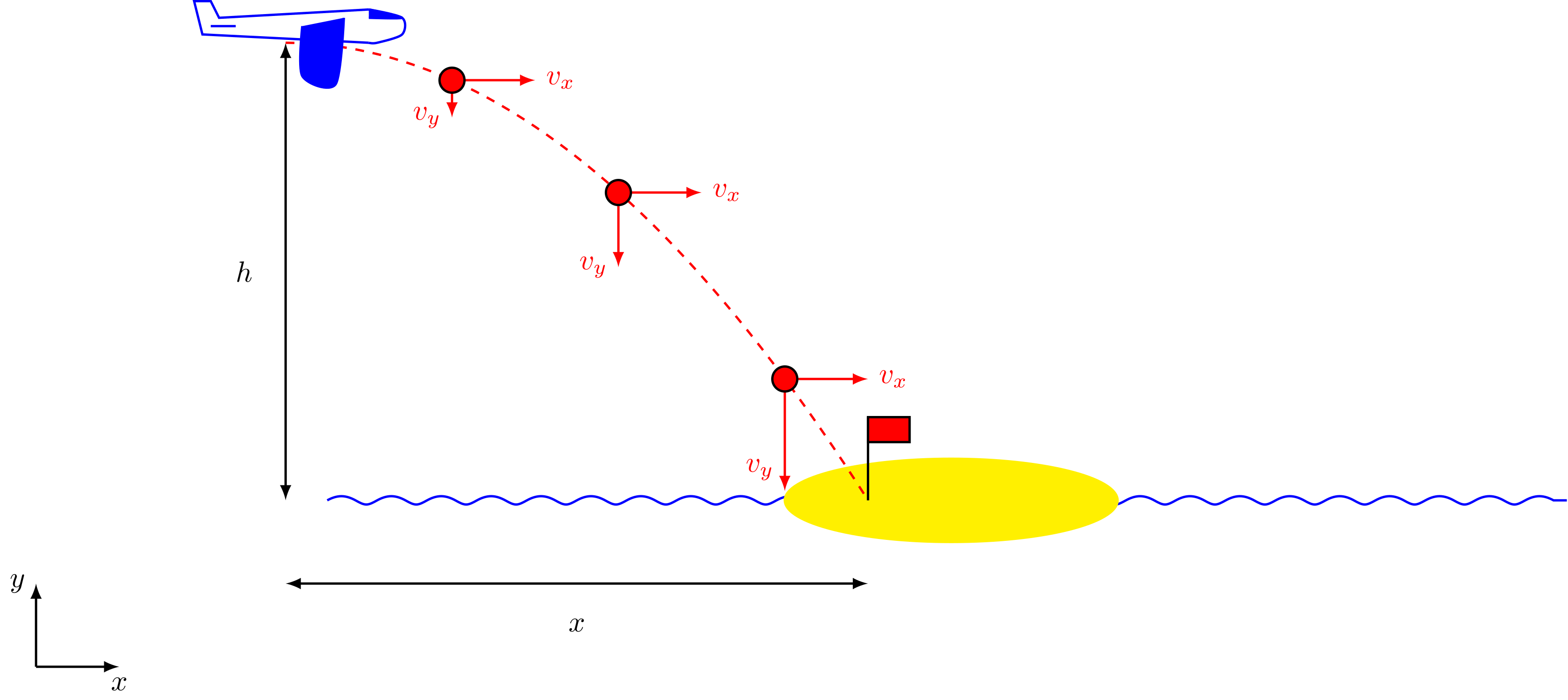
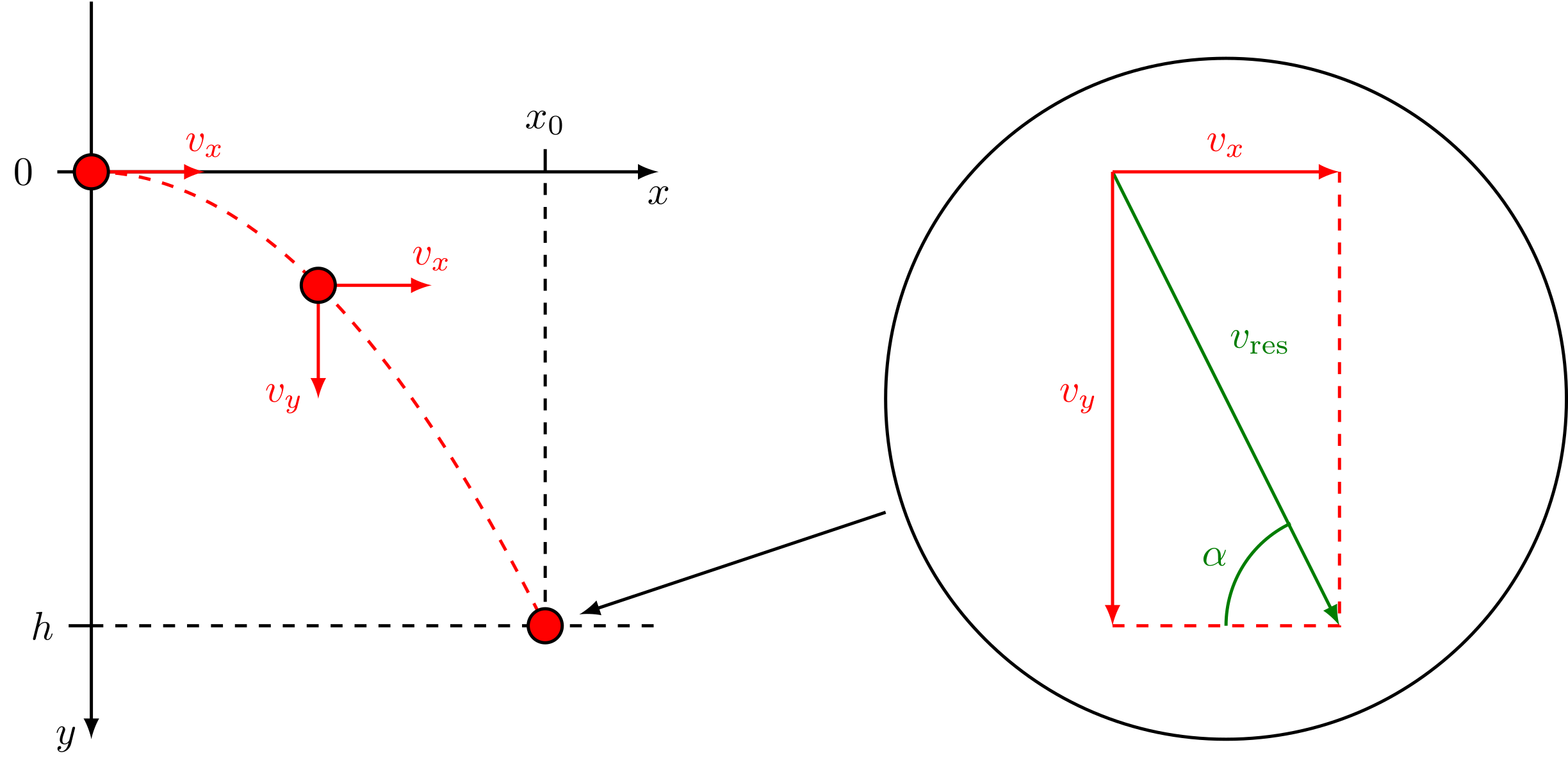
Abbildung 4.2.107: Schema waagerechter Wurf  (C)

Beispiel 4.2.41  
Sie stehen in einer Höhe von h=150 m am Rand der Aussichtsplattform des Stuttgarter Fernsehturms und wollen Versuche zum waagerechten Wurf betreiben. Es gelingt Ihnen, dem Ball eine Anfangsgeschwindigkeit von vx =10,0 m/s zu geben. Wie weit müssen Sie das Gelände um den Turm absperren, damit niemandem ein Ball auf den Kopf fällt?
Zur Lösung dieses Problems werden die Bewegungen in x-Richtung und in y-Richtung unabhängig voneinander betrachtet. Der Ursprung des Koordinatensystems wird, wie in obiger Skizze, in den Startpunkt der Bewegung gesetzt. Die bekannte Gleichung für den freien Fall kann zur Bestimmung der Flugzeit verwendet werden:
 
h= 1 2 ·g· t2   ⟺   t=± 2·h g ​ =± 2·150 m 9,81  m s2 ≈±5,53 s .
 
Die negative Lösung ist hier physikalisch nicht sinnvoll, da sie bedeuten würde, dass der Ball zeitlich vor dem Abwurf am Ziel ankommt. Mit der Gleichung für die gleichförmige Bewegung und der Flugzeit kann jetzt die Flugweite ermittelt werden:
 
vx = x0 t   ⟺   x0 = vx ·t ​≈10,0  m s ·5,53 s ​ =55,3m .
 
Unter Berücksichtigung des Durchmessers der Aussichtsplattform von D=15,0 m müssen Sie also eine kreisförmige Absperrung um den Turm mit einem Radius von mindestens r=7,5 m+55,3 m=62,8 m ziehen.
Sollte jetzt noch der Betrag der Geschwindigkeit von Interesse sein, muss die y-Komponente der Geschwindigkeit bestimmt werden:
 
vy =g·t ​≈9,81  m s2 ·5,53 s ​≈54,2  m s  .
 
Die Geschwindigkeit des Körpers kann dann als Vektor dargestellt und der Betrag berechnet werden:
 
v → =( vx vy )  ⟹   ​| v → |= vx 2 + vy 2 ​≈ (10,0  m s )2 + (54,2  m s )2 ​≈55,2  m s  .
 
 

Basiswissen „Schiefer Wurf“


Wie beim waagerechten werden bei diesem Wurf zwei Bewegungen überlagert. Allerdings wird hier der Ball in eine beliebige Richtung mit einer Geschwindigkeit v0 geworfen. Gleichzeitig erfährt der Ball ab dem Zeitpunkt eine Beschleunigung in Richtung Erde.
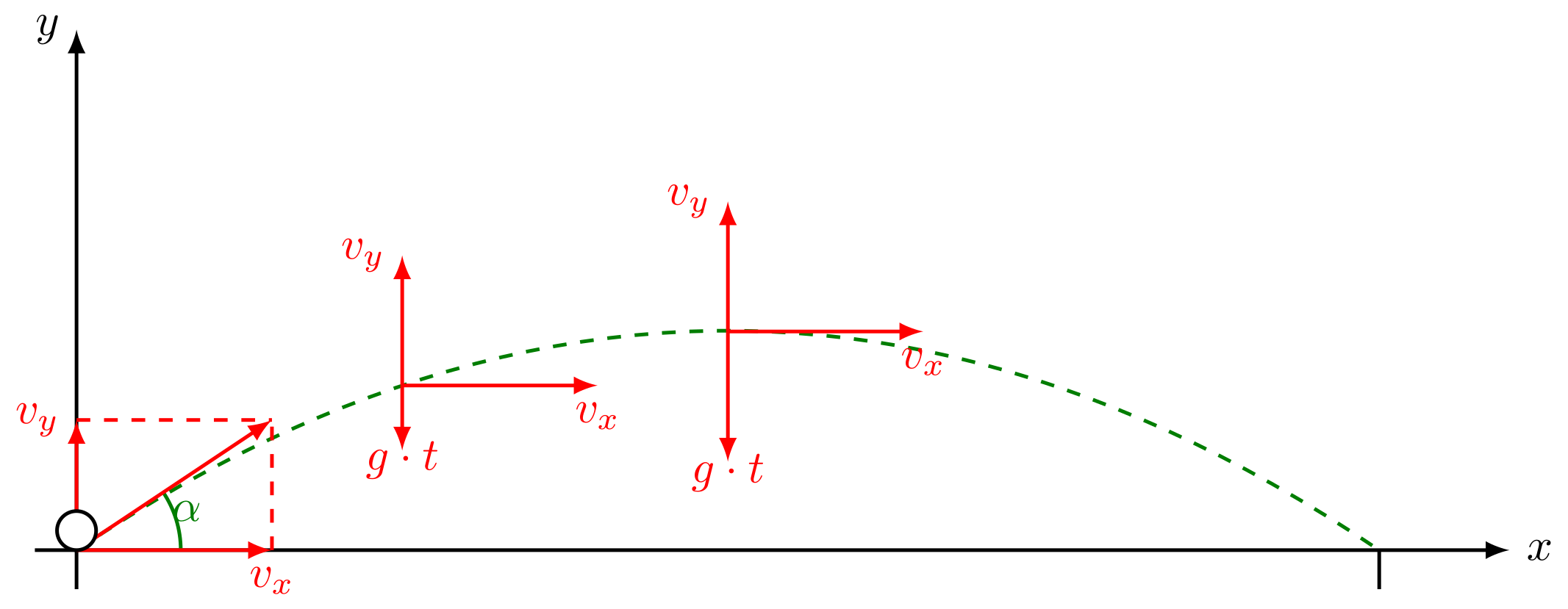
Diese Situation ist in der Abbildung links dargestellt. Der Ball wird von einem Turm unter einem Winkel α zur Horizontalen abgeworfen. Der Ball führt also eine gleichförmige Bewegung in x-Richtung und in y-Richtung aus. Zusätzlich kommt in y-Richtung der freie Fall hinzu. Die Bewegung in y-Richtung entspricht also einem senkrechten Wurf.


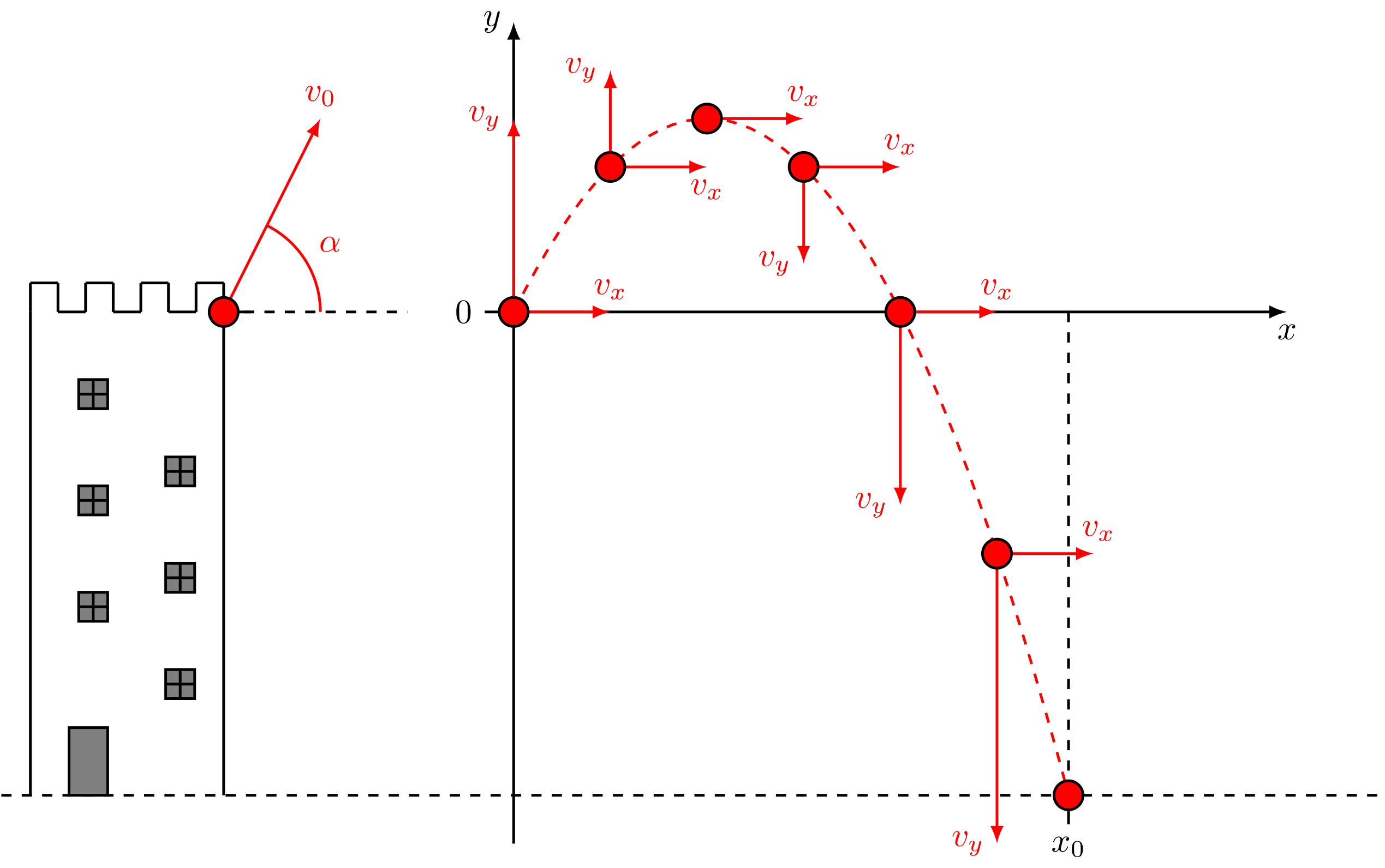
./_C3DE47EF_4x.png
Abbildung 4.2.108: Schema schiefer Wurf  (C)

In der Abbildung rechts ist die Bahn des Balles für den Fall, dass der Ball nach oben geschossen wird, dargestellt. Die Pfeile sollen die Geschwindigkeiten und ihre Beträge zu verschiedenen Zeitpunkten beispielhaft anzeigen.

  • Die Bewegung in x-Richtung verläuft bis zur Landung immer mit der gleichen Geschwindigkeit vx .

  • In y-Richtung nimmt die Geschwindigkeit vy bis zum obersten Punkt der Bahn ab. Grund ist die Beschleunigung des Körpers in Richtung Erde. Im obersten Bahnpunkt hat der Körper kurzzeitig eine verschwindende Geschwindigkeitskomponente, vy =0. Im Anschluss fällt der Ball in y-Richtung frei nach unten und wird immer schneller. Wenn der Ball seine ursprüngliche Starthöhe erreicht hat, besitzt er betragsmäßig wieder die gleiche Geschwindigkeit vy wie zum Startzeitpunkt, jedoch zeigt der Geschwindigkeitsvektor jetzt nach unten. Da der Boden tiefer liegt, fällt der Ball weiter und wird bis zur Landung immer schneller.

  • Überlagert man diese beiden Bewegungen, erhält man als Bahnkurve die gestrichelt gezeichnete Parabel.

Die für einen Wurf nach oben geltenden Gleichungen für die Geschwindigkeit lauten in vektorieller Schreibweise:
 
v → =( vx vy ) ​ =( v0 ·cosα v0 ·sinα-g·t ) ,
 
wobei v0 die Startgeschwindigkeit ist und α ihr Winkel gegen die Horizontale. Ebenso kann der in die beiden Richtungen zurückgelegte Weg als Vektor geschrieben werden:
 
s → =( sx sy ) ​ =( v0 ·cosα·t v0 ·sinα·t- 1 2 ·g· t2 ) .
 
Aufgaben zum schiefen Wurf können also mit den bereits bekannten Gesetzen für die gleichförmige Bewegung und die gleichförmig beschleunigte Bewegung bearbeitet werden. Wie beim waagerechten Wurf wird die Bewegung in zwei Bewegungen in x und y-Richtung zerlegt.
Beispiel 4.2.42  
Anlässlich der Heirat Maria Stuarts mit dem Dauphin von Frankreich wurde im Jahre 1558 mit dem schottischen Riesengeschütz Mons Meg Salut geschossen. Angeblich konnte die Kanone eine Eisenkugel unter einem Winkel von 45 ∘ etwa 1288 m weit schießen. Welche Anfangsgeschwindigkeit v0 muss das Geschoss besessen haben und wie lange war seine Flugzeit t?
Zur Lösung dieser Aufgabe ist die Anfertigung einer Skizze hilfreich.


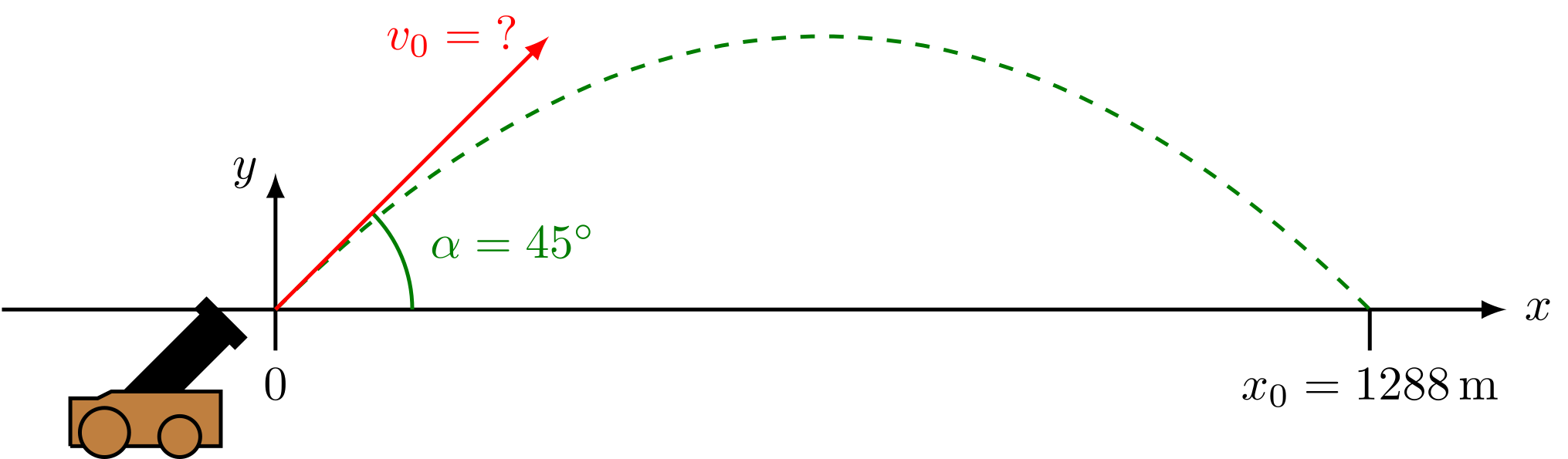
./_1FADA799_4x.png
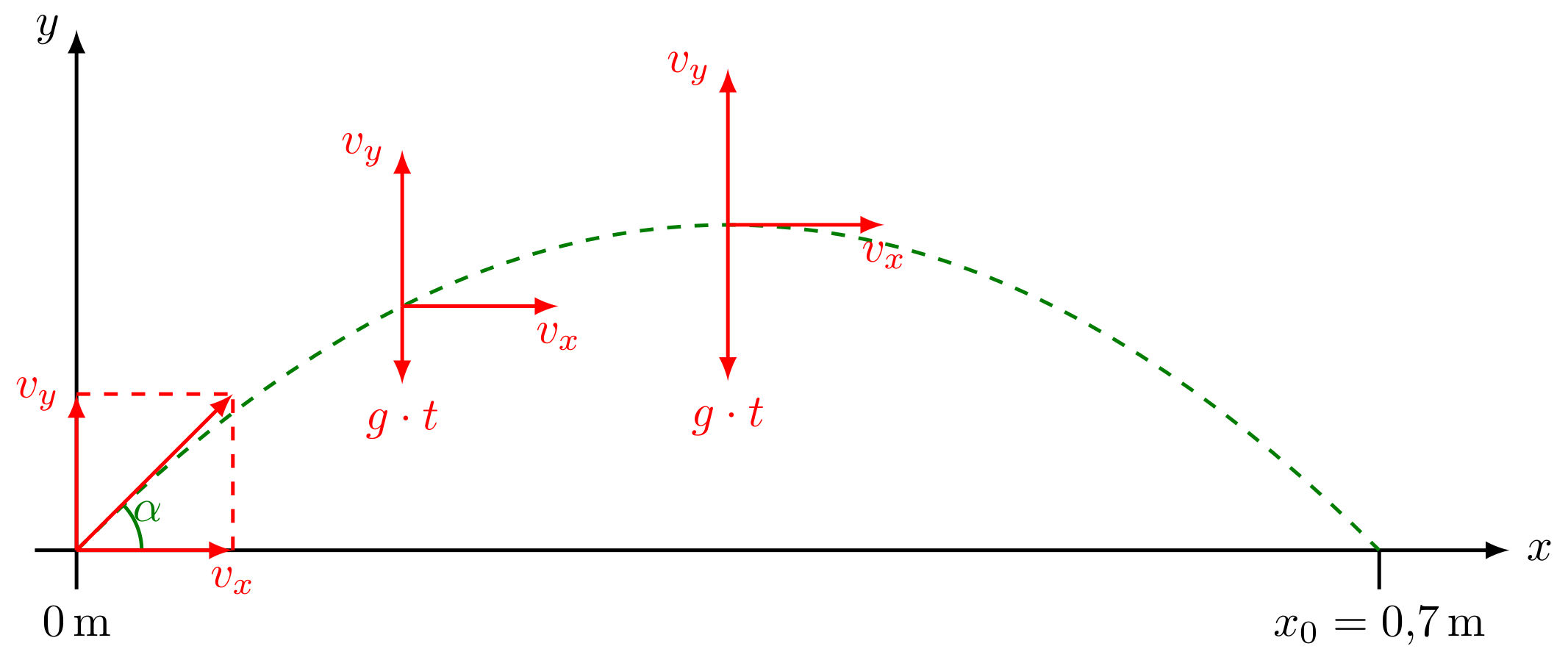
Abbildung 4.2.109: Skizze der Flugbahn beim Salutschuss  (C)

Für den Geschwindigkeitsvektor v → der Bewegung gilt in Bezug auf das gewählte Koordinatensystem:
 
v → =( vx vy ) ​ =( v0 ·cosα v0 ·sinα-g·t ) .
 
In x-Richtung ist der zurückgelegte Weg x0 bekannt. Damit kann die Flugzeit t in Abhängigkeit der noch unbekannten Anfangsgeschwindigkeit v0 bestimmt werden:
 
v0 ·cosα= x0 t   ⟺   t= x0 v0 ·cosα  .
 
In y-Richtung ist bekannt, dass die Geschwindigkeitskomponente vy im Umkehrpunkt kurzzeitig verschwindet und dass die Kugel diesen Punkt nach der halben Flugzeit erreicht:
 
vy, Scheitelpunkt =0 ​ = v0 ·sinα-g· t 2  .
 
Durch Einsetzen der Flugzeit t in diese Gleichung ergibt sich:
 
0= v0 ·sinα-g· x0 2· v0 ·cosα   ⟺   0= v0 2 ·sinα·cosα- 1 2 ·g· x0  .
 
Jetzt wird mit der Beziehung sin(2·α)=2·sinα·cosα vereinfacht und nach der Geschwindigkeit v0 umgeformt:
 
0= v0 2 · 1 2 ·sin(2·α)- 1 2 ·g· x0   ⟺   v0 2 = x0 ·g sin(2·α)  .
 
Da für den Winkel α=45 ∘ gilt und damit sin(2·α)=1, ergibt sich für den Geschwindigkeitsbetrag v0 :
 
v0 =g· x0 ​ =9,81  m s2 ·1288 m ​≈112  m s  .
 
Setzt man den Geschwindigkeitsbetrag v0 in obige Gleichung für die Flugzeit ein, erhält man:
 
t= x0 v0 ·cosα ​≈ 1288 m 112  m s · 2 2 ≈16,3 s .
 


Unter dem folgenden Link finden Sie eine Animation, die Ihnen erlaubt, mit verschiedenen Startwerten einen senkrechten, einen waagerechten und einen schiefen Wurf zu simulieren:
 
Animation zum senkrechten, waagerechten und schiefen Wurf  

Basiswissen „Ortsvektor und Bahnkurve“


Im Folgenden soll am Beispiel des schiefen Wurfes der Unterschied zwischen Ortsvektor und Bahnkurve besprochen werden. Betrachtet man die Bewegung eines Körpers im Raum, so wird der Ort, an dem sich der Körper befindet, in einem Koordinatensystem durch den Ortsvektor beschrieben. Der Ortsvektor ist ja gerade der Vektor, der vom gewählten Koordinatenursprung zu einem Punkt geht. Prinzipiell kann das Koordinatensystem frei gewählt werden.
In der Abbildung ist dies für einen schiefen Wurf gezeigt. Das Koordinatensystem wurde so gewählt, dass die x-Achse parallel und die y-Achse senkrecht zur Horizontalen liegt. Der Ursprung des Systems liegt am Abwurfpunkt. Die grüne Linie stellt die Bahn, auf der sich der Ball bewegt, dar. Sie wird Bahnkurve genannt. Die roten Pfeile sind Ortsvektoren zu verschiedenen Zeitpunkten. Der Ortsvektor ist also abhängig von der Zeit: r → = r → (t).


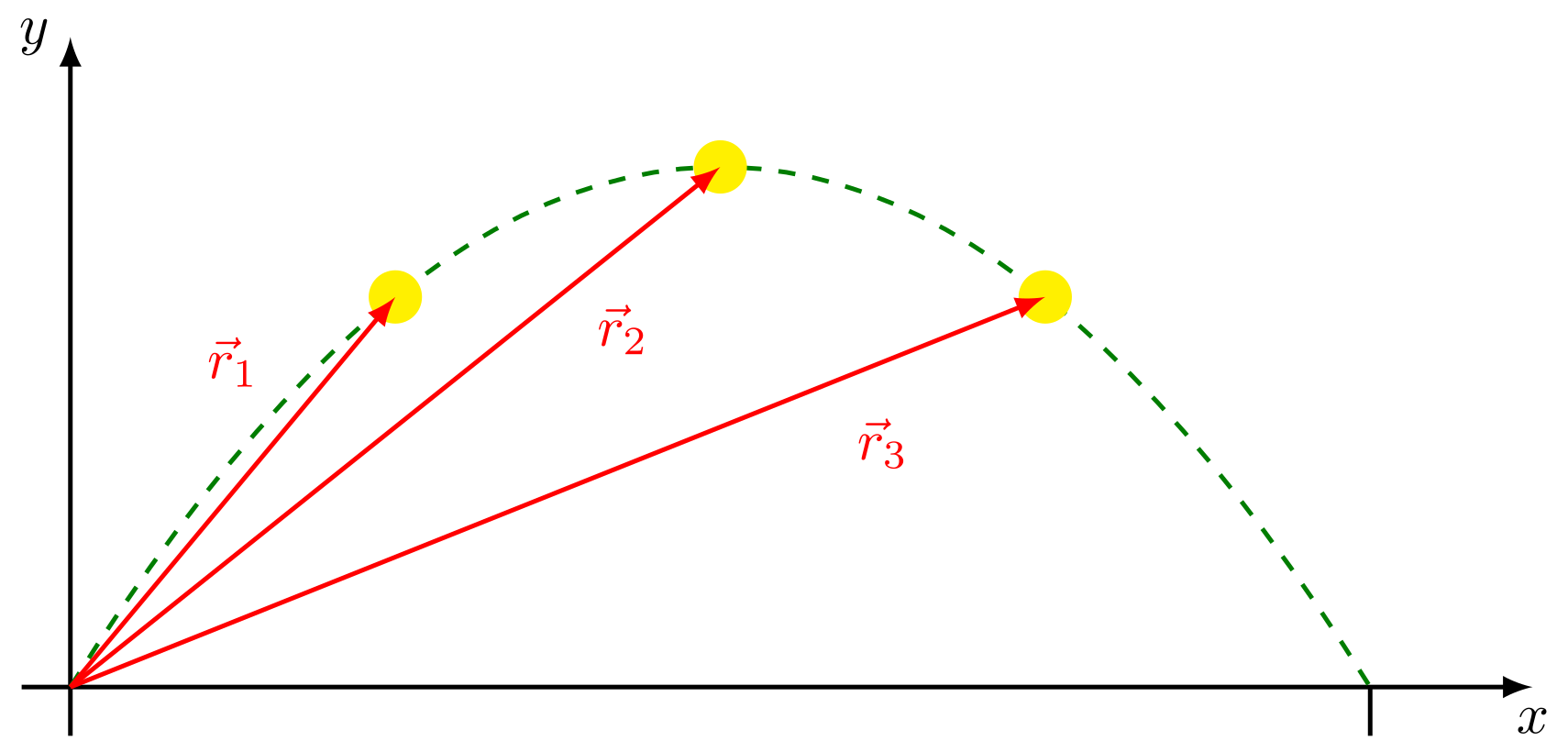
./_261ED692_4x.png
Abbildung 4.2.110: Illustration zu Ortsvektor und Bahnkurve  (C)

Der Ortsvektor des Balles zu jedem Zeitpunkt lässt sich für das gewählte Beispiel mit Hilfe der Orts-Zeit-Funktionen aufschreiben:
 
r → (t)=( rx (t) ry (t) ) ​ =( v0 ·cosα·t v0 ·sinα·t- 1 2 ·g· t2 ) .
 
Dabei wird der Ball mit der Geschwindigkeit v0 unter dem Winkel α gegen die Horizontale abgeworfen.
Aus diesem Ortsvektor kann die Gleichung für die Bahnkurve hergeleitet werden. Dazu wird die Beziehung für die x-Koordinate nach t umgeformt:
 
x= v0 ·cosα·t   ⟺   t= x v0 ·cosα  .
 
Diese Gleichung für die Zeit wird nun in die y-Koordinate eingesetzt:
 
y=​ v0 ·sinα· x v0 ·cosα ​- 1 2 ·g· ( x v0 ·cosα )2 ​ =tanα·x- g 2· v0 2 · cos2 α · x2  .
 
Durch diese Gleichung wird der Zusammenhang zwischen der x-Koordinate und y-Koordinate während der Bewegung hergestellt. Die Bahnkurve ist unabhängig von der Zeit. Sie entspricht einer nach unten geöffneten Parabel (allgem. Form y(x)=a· x2 +b·x+c).

Wenn in den folgenden Aufgabentexten nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie g=9,81  m s2  .
Aufgabe 4.2.43  
Der Pilot eines Flugzeuges soll über der in der Abbildung gezeigten Insel Proviant abwerfen. Die Lieferung soll an der Fahne landen. In welcher Entfernung vor der Fahne muss der Pilot die Last abwerfen? Die Geschwindigkeit des Flugzeuges beträgt vx =180 km/h und die Flughöhe liegt bei h=400 m.

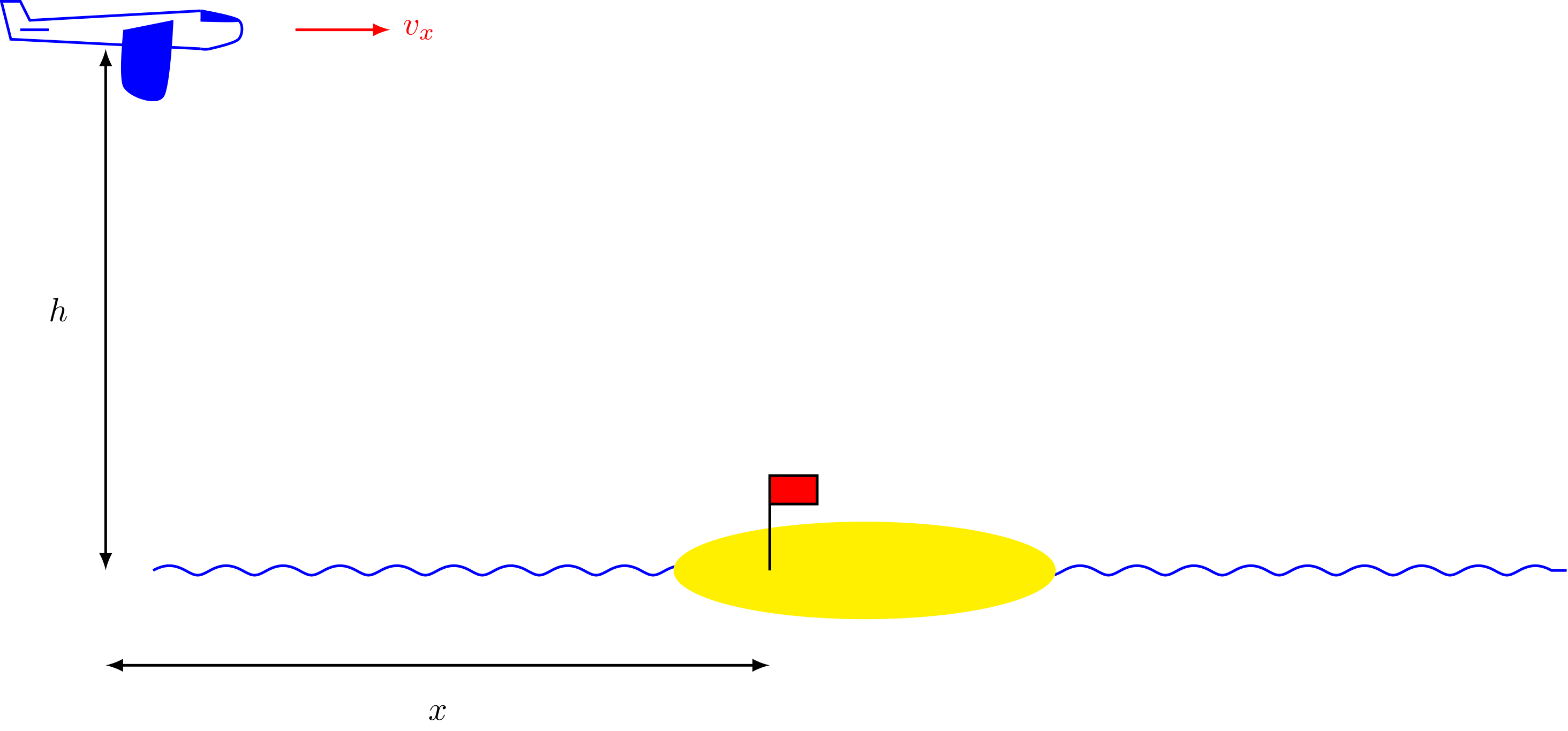
./_F360913F_4x.png
Abbildung 4.2.111: Flugzeug wirft Proviant ab  (C)

Direkt über der Fahne, da der Proviant im freien Fall fällt und dann punktgenau landet.
Das kann man mit diesen Angaben nicht berechnen.
Etwa 450 m vor dem Ziel.
Etwa 1625 m vor dem Ziel.
Etwa 450 m hinter dem Ziel.



Aufgabe 4.2.44  
Der Pilot eines Flugzeuges soll über der Insel Makura dringend benötigte Güter abwerfen. Die Lieferung soll an der Fahne landen. Wie lange vor Überfliegen des Ziels muss der Pilot die Ladung abwerfen und in welcher Entfernung x vor der Fahne befindet er sich zu diesem Zeitpunkt? Die Geschwindigkeit des Flugzeuges beträgt vx =220 km/h und die Flughöhe liegt bei h=300 m.
 
./_F360913F_4x.png
Abbildung 4.2.113: Flugzeug wirft Proviant ab  (C)

t  = 


x  = 




Aufgabe 4.2.45  
Bei einem Wettkampf im Kugelstoßen misslingt dem Favoriten der Stoß. Er stößt die Kugel waagerecht von seiner Schulter ( h=1,55 m) weg. In einer Entfernung von x=17,2 m kommt sie zum Liegen. Machen Sie sich die Situation anhand einer Skizze klar.
 
Welche Zeit t war die Kugel unterwegs?

t  = 


Mit welcher Geschwindigkeit vx wurde sie gestoßen?

vx  = 


Unter welchem Winkel α gegen die Horizontale landet sie auf dem Boden?

α  = 
∘

Wie groß ist dabei der Betrag der Geschwindigkeit?

| v → |  = 




Aufgabe 4.2.46  
Ein Fußballer schafft es, einen Ball mit einer Geschwindigkeit von v=120 km/h unter einem Winkel von 34 ∘ zu schießen. Nach welcher Zeit trifft der Ball aus den Boden auf?
Nehmen Sie an, dass der Ball in Bodenhöhe getroffen wurde.

t ges  = 




Aufgabe 4.2.47  
Eine Waldmaus kann etwa 0,7 m weit springen. Wie hoch springt sie unter der Annahme, dass ihre Flugbahn einem schiefen Wurf entspricht? Der Absprungwinkel soll bei 45 ∘ und die Absprunggeschwindigkeit bei 2,6 m/s liegen.

Verwenden Sie zur Berechnung lediglich die letzten beiden Angaben.

h  = 




Aufgabe 4.2.48  
In Acapulco springt ein Klippenspringer vom bekannten Felsen La Quebrada. Er springt mit einer Geschwindigkeit von 5,0 m/s unter einem Winkel von 30 ∘ gegen die Horizontale nach oben ab. Der Startpunkt liegt 35 m über der Wasseroberfläche. Wie weit bewegt sich der Klippenspringer in x-Richtung durch die Luft?
Zur Veranschaulichung ist in der Abbildung die Situation skizziert.
 
./_F801D29E_4x.png
Abbildung 4.2.118: Sprung des Klippenspringers  (C)

x0  = 




Aufgabe 4.2.49  
Der Pilot eines Flugzeuges soll über der in der Abbildung gezeigten Insel Proviant abwerfen. Die Lieferung soll an der Fahne landen. Die Geschwindigkeit des Flugzeuges beträgt vx =234 km/h. Welche Flughöhe ist nötig, wenn das Flugzeug 570 m in horizontaler Richtung vor dem Ziel die Ladung abwirft?
Bestimmen Sie zuerst die Bahngleichung für die abgeworfene Ladung und berechnen Sie damit die gesuchte Größe.
 
./_F360913F_4x.png
Abbildung 4.2.119: Flugzeug wirft Proviant ab  (C)





 

Unabhängigkeit von Bewegungen (!)
Video 37: Unabhängigkeit von Bewegungen (C) .

Um zweidimensionale Bewegungen zu beschreiben, berücksichtigt man das Prinzip der Unabhängigkeit verschiedener Bewegungen des gleichen Körpers. Man kann z.B. die Gesamtbewegung eines Körpers in zwei geradlinige Bewegungen in unterschiedliche Richtungen aufteilen, die unbeeinflusst voneinander ablaufen. Die Überlagerung zweier gleichförmiger Bewegungen mit konstanter Geschwindigkeit ist einsichtig:

  • Ein Fußgänger bewegt sich mit der Geschwindigkeit v1 auf einem Rollsteig (ebene Rolltreppe), der mit der Geschwindigkeit v2 läuft. In diesem Fall addieren sich die beiden Geschwindigkeiten zur Gesamtgeschwindigkeit des Fußgängers:

    v= v1 + v2  .



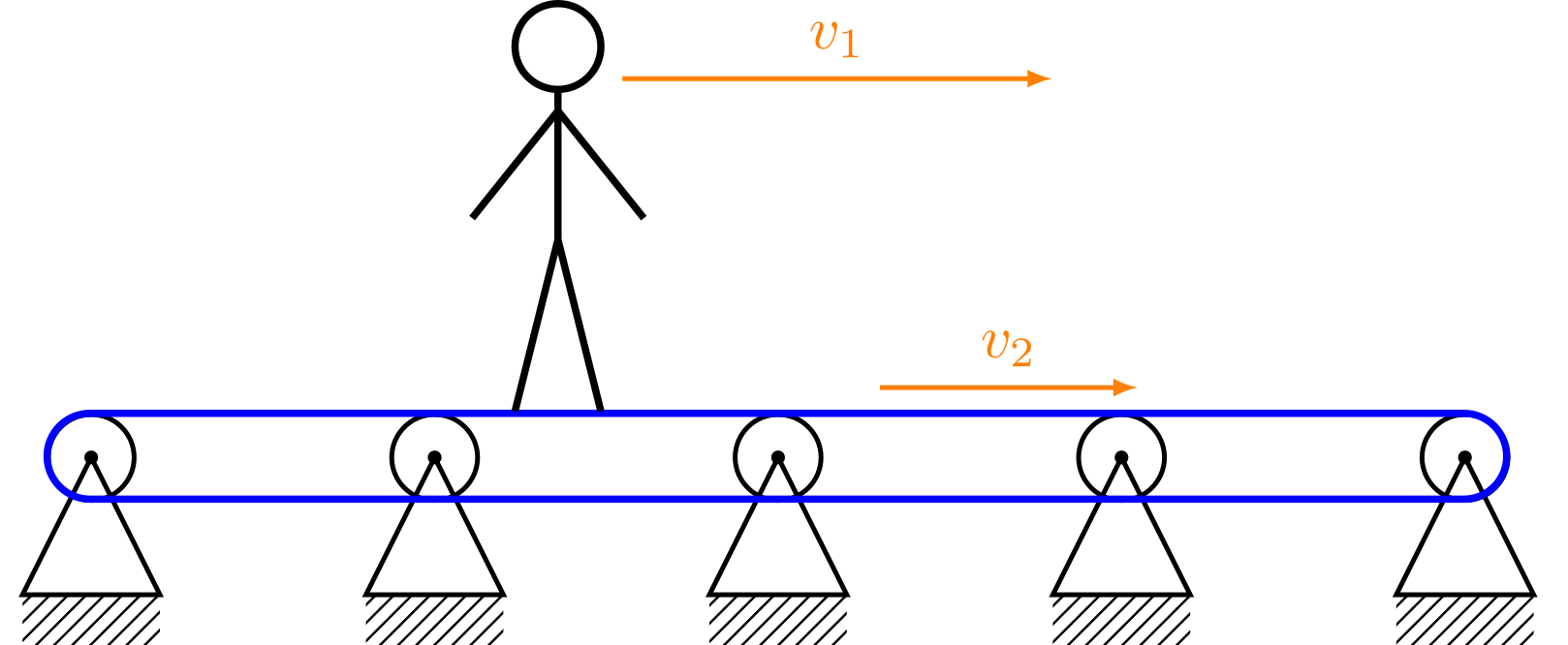    ./_CFDBF46A_4x.png
    Abbildung 4.2.121: Fußgänger läuft auf Rollsteig  (C)



  • Ein Schwimmer schwimmt mit der Schwimmgeschwindigkeit v → 1 im Wasser quer über einen Fluss, der eine Strömungsgeschwindigkeit von v → 2 besitzt. Dann addieren sich die beiden Geschwindigkeiten vektoriell:

    v → = v → 1 + v → 2  .

    Richtung und Geschwindigkeitsbetrag des Schwimmers sind durch den Summenvektor v → gegeben.

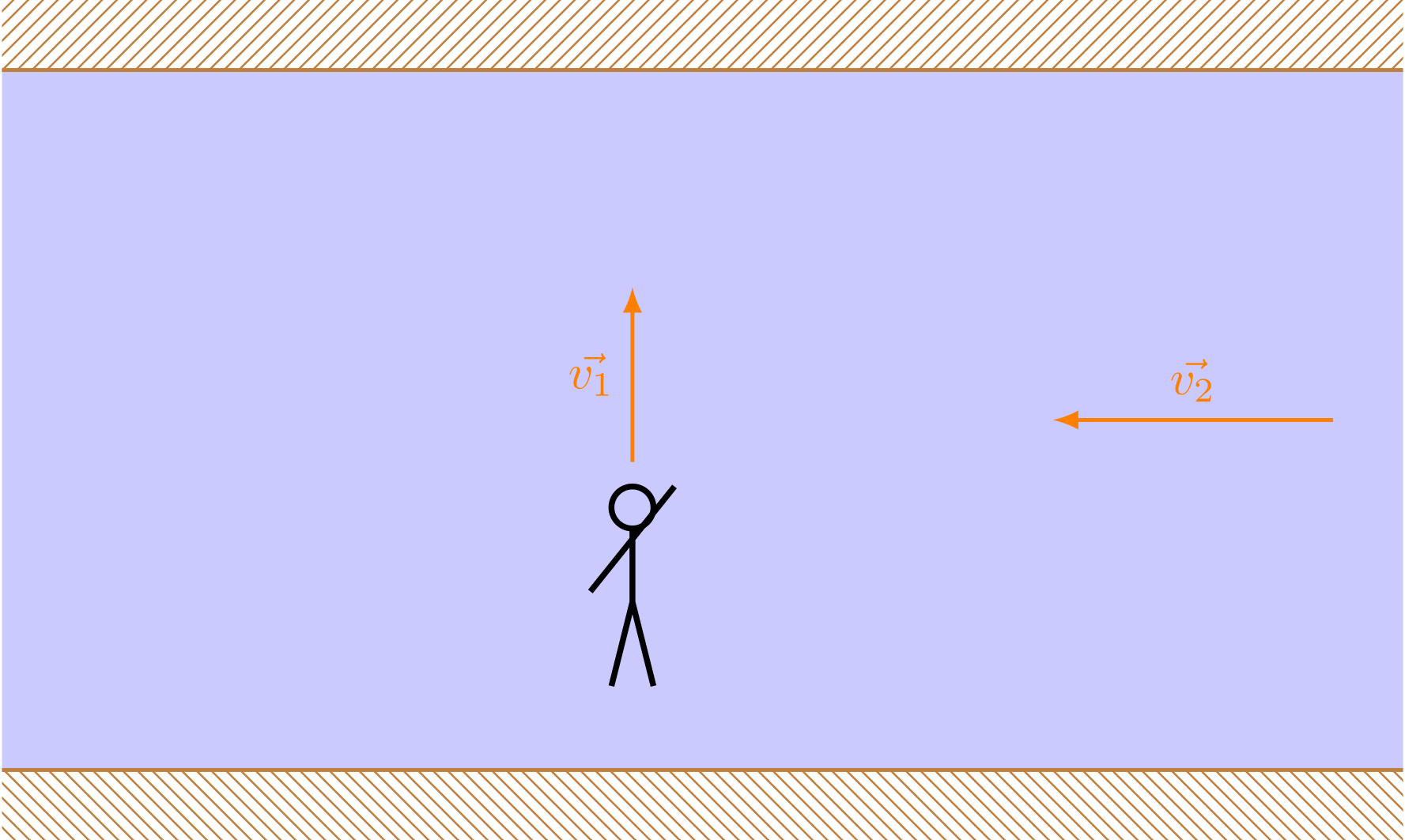    ./_FE2F4903_4x.png
    Abbildung 4.2.122: Schwimmer durchquert Fluss  (C)





Video 38: Unabhängigkeit von Bewegungen: Beispiel (C) .

Video 39: Unabhängigkeit von Bewegungen: Beispiel (C) .

Video 40: Unabhängigkeit von Bewegungen: Beispiel (C) .

Video 41: Unabhängigkeit von Bewegungen: Beispiel (C) .



Ist eine der beiden Bewegungen beschleunigt, wird die Anschauung etwas schwieriger:

  • Ein Körper benötigt für den Fall aus 5 m Höhe eine Fallzeit von ca. 1 s. Dabei ist es gleichgültig, ob er senkrecht herunterfällt oder ob er während des Fallens noch mehrere hundert Meter parallel zur Erdoberfläche fliegt. Die Fallbewegung „interessiert“ sich also nicht für die gleichzeitig stattfindende horizontale Bewegung. Dies leuchtet manchen Menschen nicht direkt ein.

  • Wirft man einen Körper unter einem Winkel α relativ zur Horizontalen, so bezeichnet man dies als „schiefen Wurf“ (oder auch „schrägen Wurf“). Auch hier besteht die Bewegung aus der Überlagerung zweier unabhängiger Bewegungen. Die eine ist die gleichförmige Bewegung in horizontaler Richtung, die andere ist eine beschleunigte Bewegung in vertikaler Richtung. Überlagert man beide Bewegungen, so entsteht eine parabelförmige Bahnkurve, die sogenannte Wurfparabel.

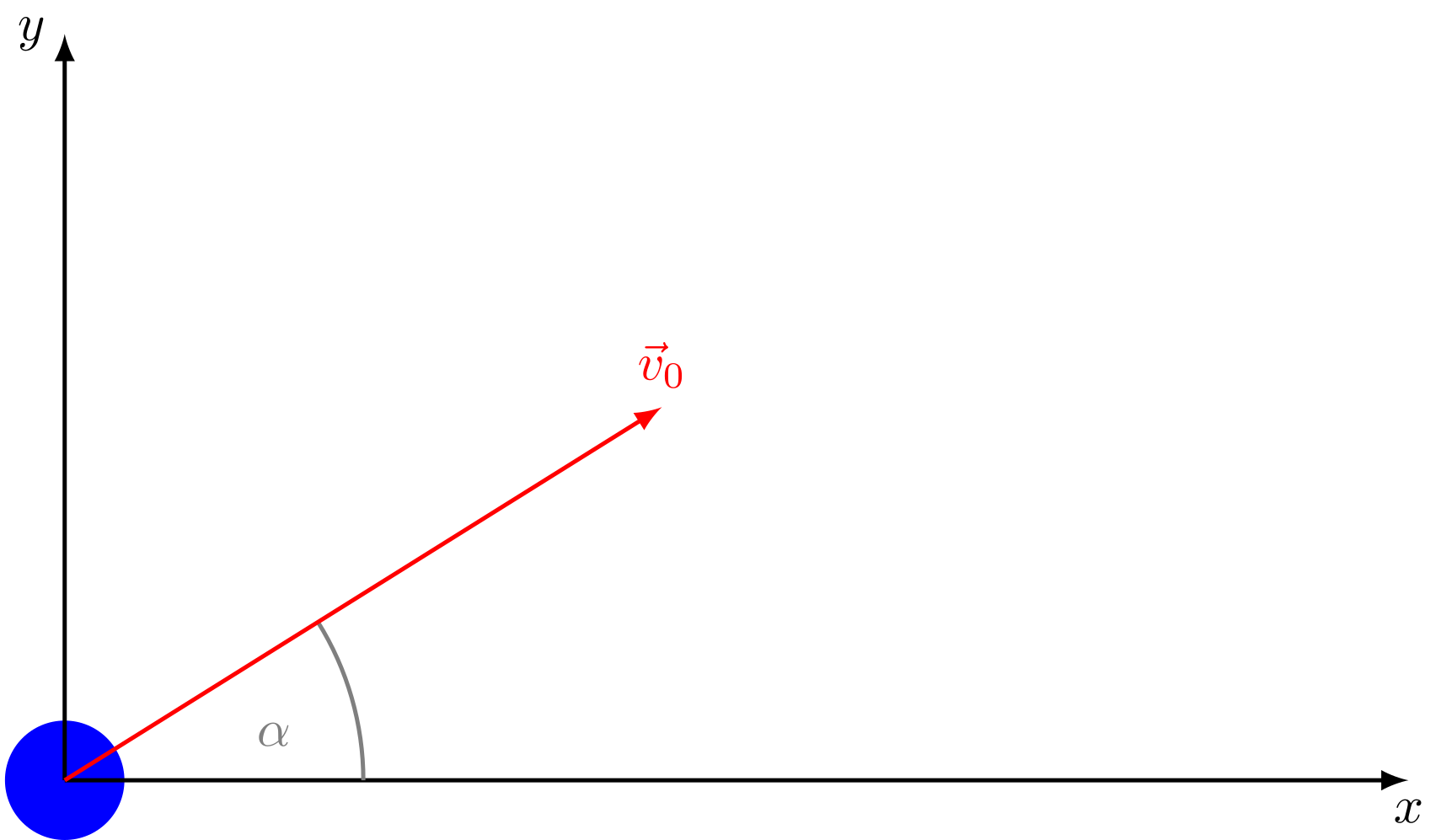    ./_C828F043_4x.png
    Abbildung 4.2.123: Schieferwurf  (C)





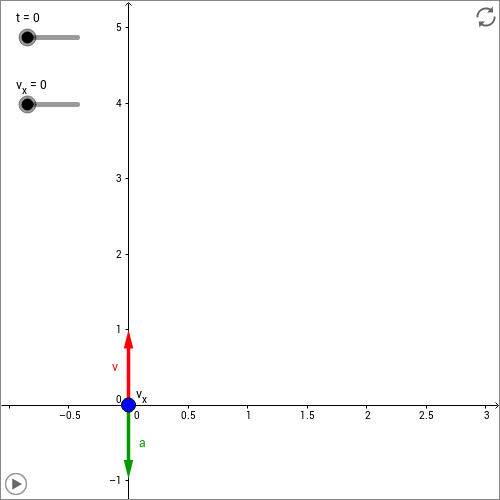
Das soeben Gesagte sei nochmals an folgender interaktiver Skizze illustriert. Man sieht hier als Beispiel einen Wurf, der vom Ursprung des Koordinatensystems ausgeht. Die vertikale Anfangsgeschwindigkeit beträgt v0 y =10 m/s, die horizontale Anfangsgeschwindigkeit kann im Bereich 0 m/s< v0 x <2 m/s gewählt werden.

Belassen Sie v0 x zunächst bei dem voreingestellten Wert von 0 m/s und starten Sie die Animation durch Klicken auf das Symbol links unten in der Ecke. Sie beobachten eine geradlinige beschleunigte Bewegung senkrecht nach oben.

Setzen Sie nun durch Klicken auf das Symbol rechts oben in der Ecke die Animation wieder zurück. Wählen Sie eine kleine Geschwindigkeit v0 x >0 und starten Sie die Animation erneut. Sie beobachten, wie sich der Körper zusätzlich zur senkrechten Bewegung nun auch nach rechts bewegt und dadurch eine parabelförmige Bahnkurve zurücklegt.

Am Körper sind die drei Vektoren eingezeichnet, die seine Bewegung bestimmen, und zwar die beiden Geschwindigkeitskomponenten vx und vy sowie der Beschleunigungsvektor a → .

././Physikkurs/bewegung_zweidimensional/images/geogebra_bewegung_standbild10.png
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)



 

Bewegungsgesetze beim schiefen Wurf (!)
Video 42: Bewegungsgesetze beim schiefen Wurf: Orts-Zeit-Gesetz (C) .

Video 43: Bewegungsgesetze beim schiefen Wurf: Geschwindigkeits-Zeit-Gesetz (C) .

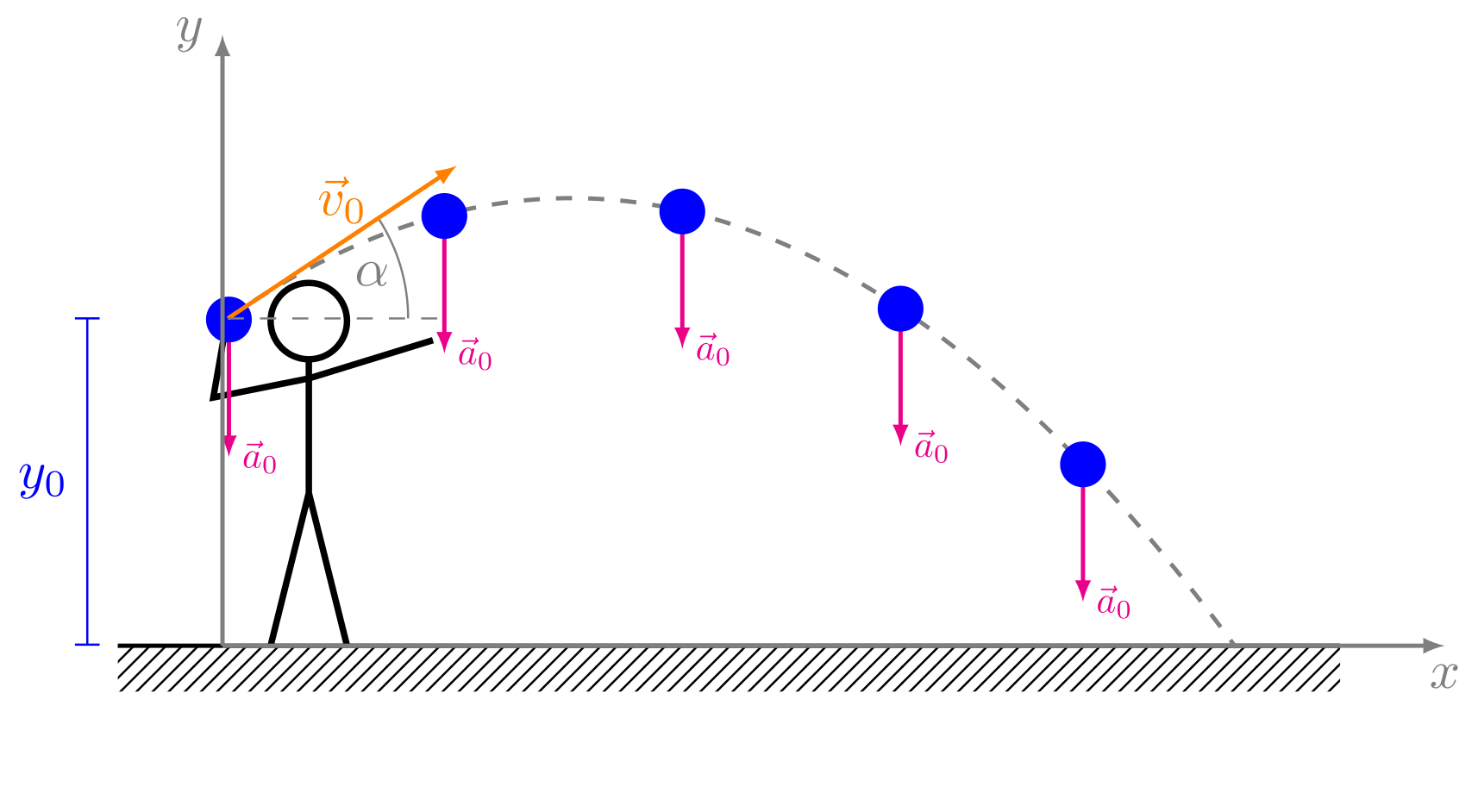
./_CF1A7DD7_4x.png
Abbildung 4.2.125: Wurfparabel eines schiefen Wurfs  (C)

Der schiefe Wurf ist die Überlagerung einer gleichförmigen Bewegung in horizontaler Richtung ( x-Richtung) und einer beschleunigten Bewegung in vertikaler Richtung ( y-Richtung). Der Wurf startet zur Zeit t=0 am Ort (0, y0 ) mit der Anfangsgeschwindigkeit v → 0 . Das Koordinatensystem wird also so gelegt, dass der Wurf bei x=0 beginnt. Man erlaubt allerdings eine Anfangshöhe y0 über der Erdoberfläche. Damit erhält man die nachfolgend aufgeführten Zeitabhängigkeiten.
Horizontale Richtung:

ax (t) = 0 , vx (t) = v0 x  , x(t) = v0 x  t .

Vertikale Richtung:

ay (t) = -g , vy (t) = -g t+ v0 y  , y(t) = - 1 2  g  t2 + v0 y  t+ y0  .

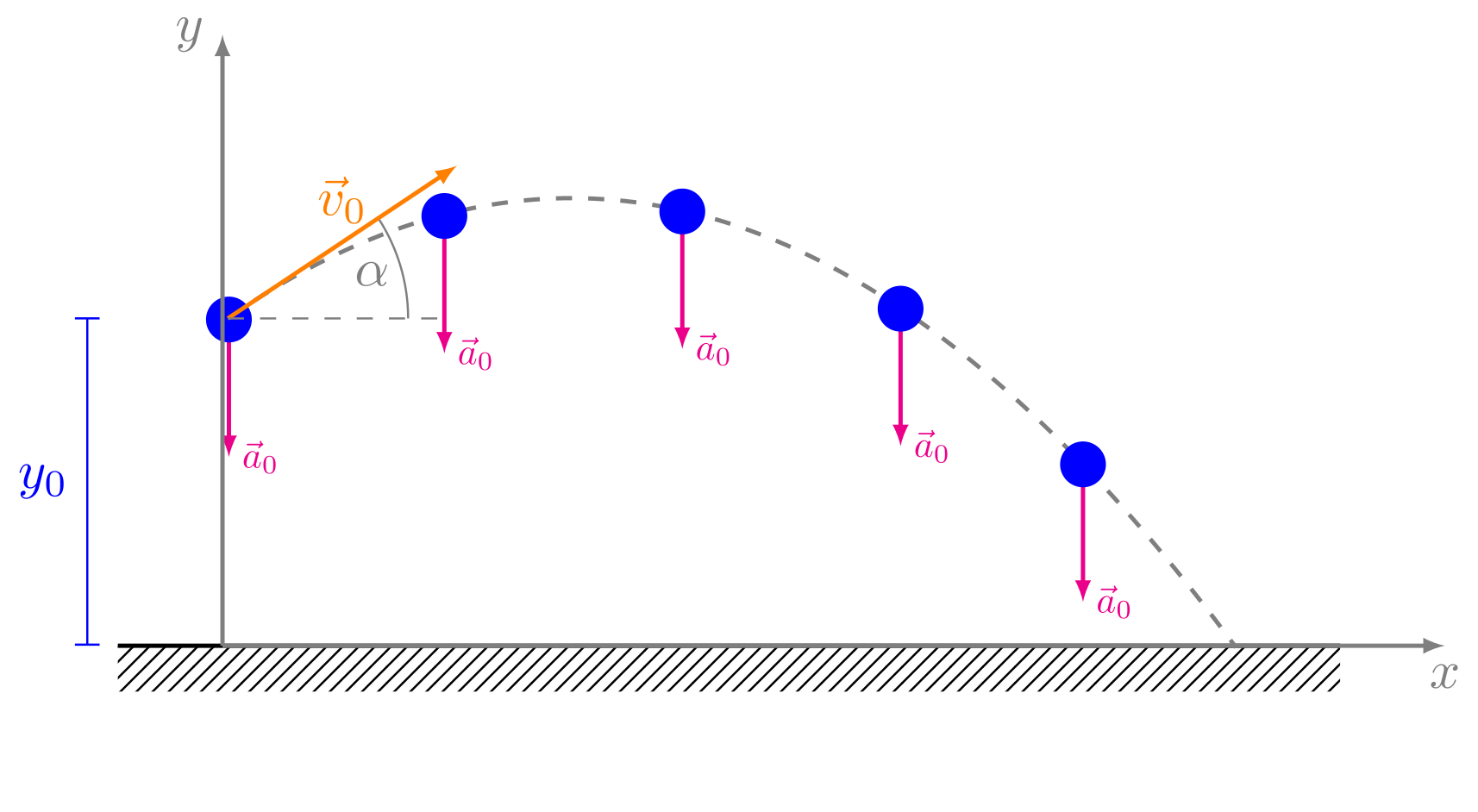
./_6F59CE71_4x.png
Abbildung 4.2.126: Wurfparabel eines schiefen Wurfes  (C)

Diese Zeitabhängigkeiten kann man auch kompakt in einer Vektorschreibweise zusammenfassen. Hierbei benutzt man zweikomponentige Vektoren, da die dritte Koordinate für die vorliegende zweidimensionale Bewegung nicht benötigt wird:

a → (t) = ( 0 -g ) , v → (t) = ( v0 x -g t+ v0 y ) , r → (t) = ( v0 x  t - 1 2  g  t2 + v0 y  t+ y0 ) .

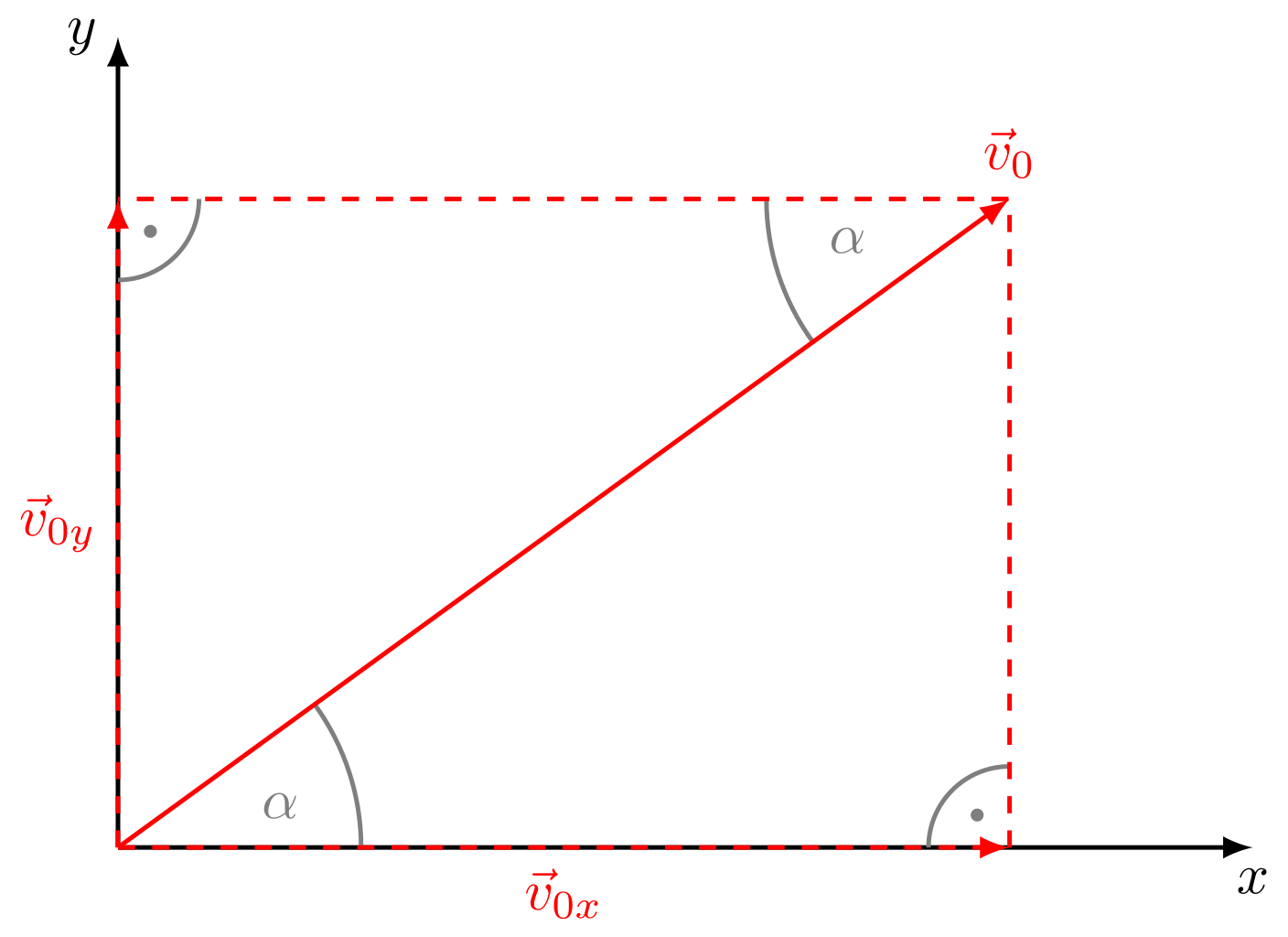
./_FF91A99B_4x.png
Abbildung 4.2.127: Zerlegung des Geschwindigkeitsvektor  (C)

Zur Zeit t=0 wird der Körper mit der Geschwindigkeit v → 0 unter einem Winkel α relativ zur Horizontalen geworfen. Die Werte für die Geschwindigkeitskomponenten v0 x und v0 y erhält man durch einfache Trigonometrie:

v0 x = v0  cosα , v0 y = v0  sinα .



 

Wurfhöhe und Wurfweite (+)
Video 44: Berechnung der Wurfhöhe (C) .

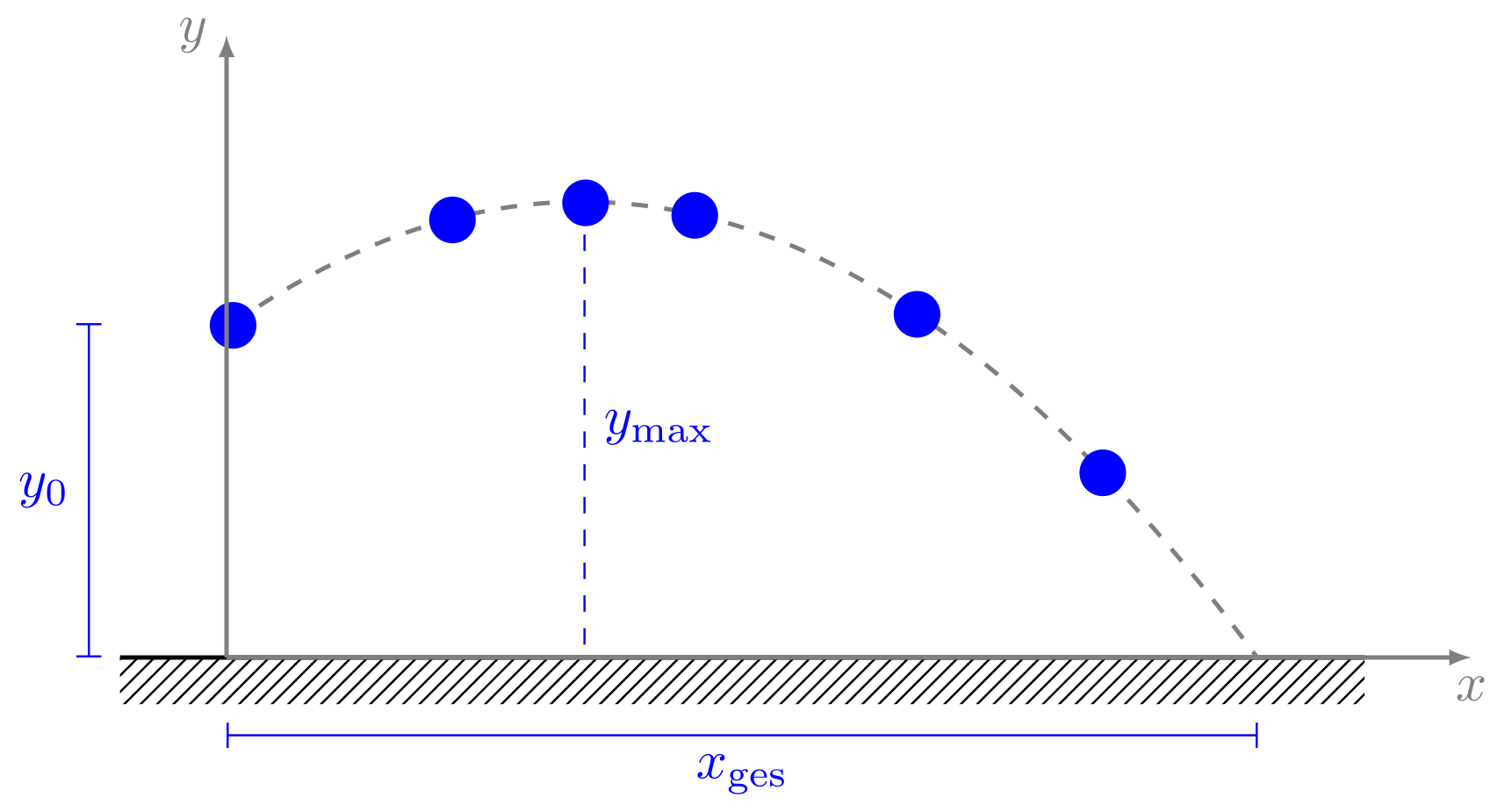
./_F52F3F77_4x.png
Abbildung 4.2.128: Wurfhöhe beim schiefen Wurf  (C)

Da die vertikale und die horizontale Bewegung jeweils unabhängig voneinander sind, kann man zunächst nur die Vertikalbewegung alleine betrachten. Sowohl die Wurfhöhe als auch die Wurfdauer entsprechen den Ergebnissen, die wir beim senkrechten Wurf erhalten hatten. Beim senkrechten Wurf war die Wurfhöhe:

h= 1 2   v W 2 g  ,

wobei v W die vertikale Abwurfgeschwindigkeit ist. Die Zeit bis zum Erreichen der maximalen Wurfhöhe ist

t W = v W g  .



Im Fall des schiefen Wurfs beträgt die Vertikalkomponente der Anfangsgeschwindigkeit v0 y . Dazu wird der Körper von einer Anfangshöhe y0 aus nach oben geworfen. Damit ergibt sich für die Wurfhöhe y max :

y max = 1 2   v0 y 2 g + y0  .

Video 45: Berechnung der Wurfweite (C) .

Um die gesamte Wurfdauer zu berechnen, muss man zur Aufstiegszeit, die durch die Abwurfgeschwindigkeit festgelegt ist, und die Dauer des freien Falls aus der Abwurfhöhe y max addieren:
 
t ges = v0 y g + 2  y max g ​ = v0 y g + v0 y 2 g2 + 2  y0 g ​ = v0 y g (1+1+ 2 g  y0 v0 y 2 ) .
 


Im Fall y0 =0 ergibt sich

t ges = 2 v0 y g  ,

also die doppelte Aufstiegszeit des senkrechten Wurfs, wie man es aus Symmetriegründen (Aufstiegszeit = Fallzeit) auch erwartet.

Von der Vertikalbewegung unabhängig erfolgt in horizontaler Richtung eine gleichförmige Bewegung mit der konstanten Geschwindigkeit v0 x . So erhält man die Wurfweite x ges einfach, indem man v0 x mit der Wurfdauer t ges multipliziert:
 
x ges = v0 x   t ges ​ = v0 x v0 y g (1+1+ 2 g  y0 v0 y 2 ) .
 


Video 46: Schiefer Wurf: Beispiel (C) .



 

Bahnkurve (Trajektorie) des schiefen Wurfs (+)
Video 47: Die Bahnkurve des schiefen Wurfs (C) .

Wir wollen nun die Bahnkurve beim schiefen Wurf ermitteln. Hierfür wechselt man von der Parameterdarstellung r → (t)=(x(t),y(t)) in die Funktionsdarstellung y(x). Dafür muss die Zeitkoordinate t eliminiert werden. Horizontal bewegt sich der Körper mit konstanter Geschwindigkeit. Daher besteht zwischen t und der Koordinaten x folgende Beziehung:

t= x v0 x  .

Einsetzen in y(t) ergibt:
 
y(t)=- 1 2  g  t2 + v0 y  t+ y0 ​ =- 1 2  g  ( x v0 x )2 + v0 y   x v0 x + y0
⟹   y(x)=- g 2  v0 x 2   x2 + v0 y v0 x  x+ y0  .
 
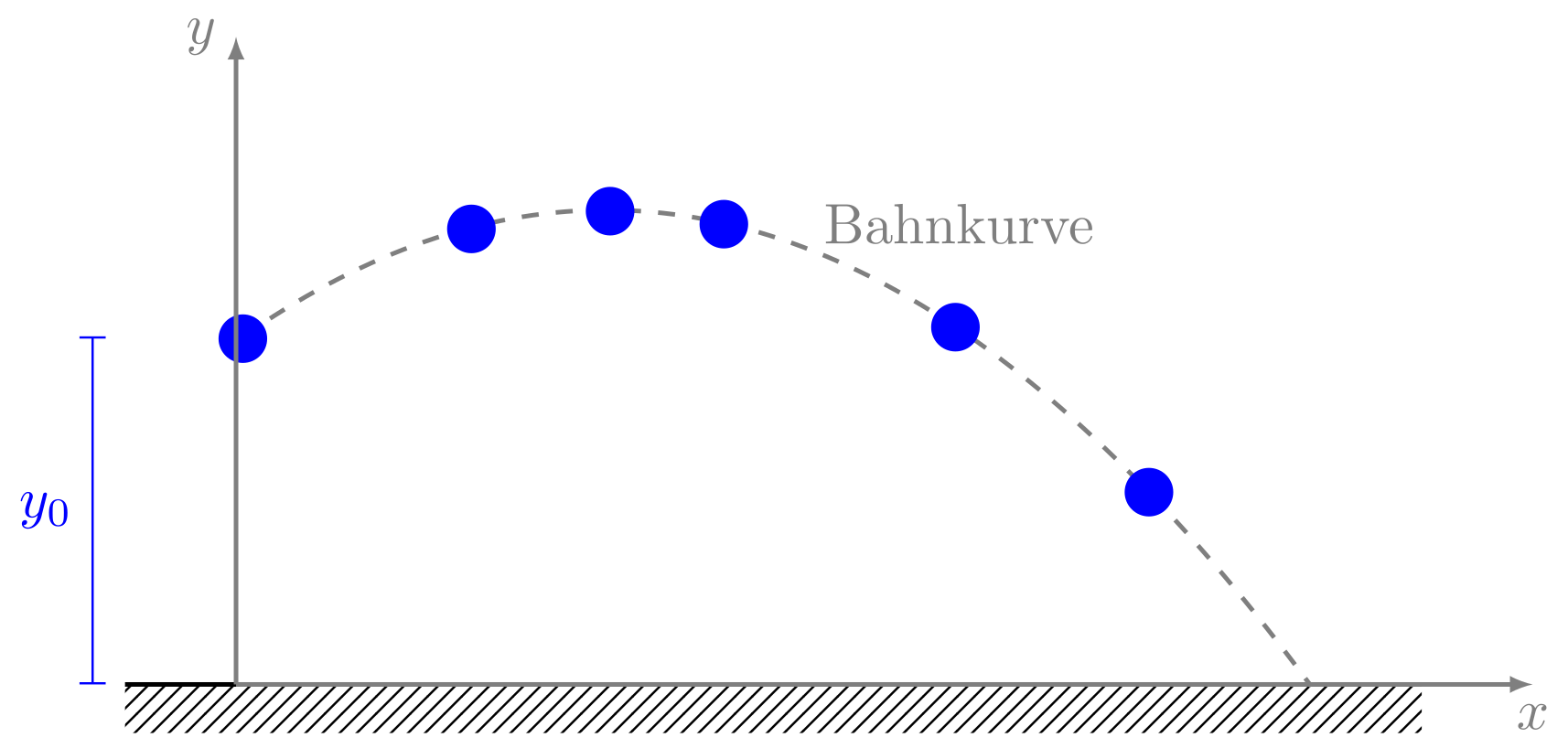
./_9835CB99_4x.png
Abbildung 4.2.129: Bahnkurve des schiefen Wurfs  (C)

Die Bahnkurve des schiefen Wurfs ist also von der Form einer Parabel, wie man an der mathematischen Form der Funktionsgleichung y(x) leicht erkennen kann. Man spricht von einer sogenannten Wurfparabel.

Drückt man die Geschwindigkeitskomponenten durch den Betrag der Abwurfgeschwindigkeit v0 und den Winkel α aus, so ergibt sich schließlich

y(x)=- g 2  v0 2   cos2 α   x2 +tanα x+ y0  .




In der folgenden Skizze ist die Wurfparabel des schiefen Wurfs gezeichnet. Anfangs- und Randbedingungen sind eine Abwurfgeschwindigkeit von v0 =10 m/s und natürlich die Erdbeschleunigung von g=9,81 m/ s2 .

Variieren Sie durch Ziehen am grünen Punkt den Abwurfwinkel α sowie durch Ziehen am blauen Punkt die Abwurfhöhe y0 .

Bei welchem Winkel α ist die Wurfweite maximal, wenn man vom Erdboden ( y0 =0) abwirft?

Welche Winkel α ergeben die maximale Wurfweite für erhöhte Abwürfe ( y0 >0)?

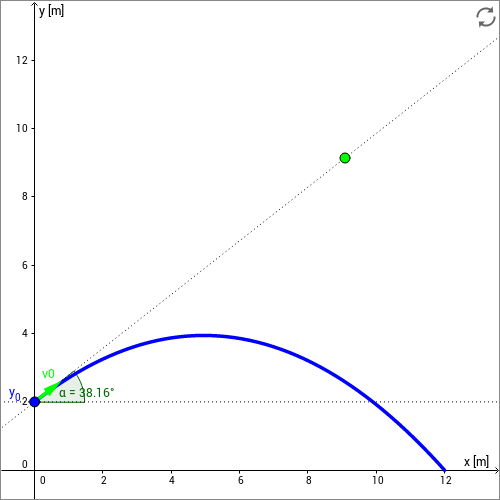././Physikkurs/bewegung_zweidimensional/images/geogebra_bewegung_standbild11.png
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)

 

Maximale Wurfweite (*)
Video 49: Berechnung der maximal möglichen Wurfweite (C) .

In der vorherigen Skizze konnten Sie ein Gefühl dafür bekommen, unter welchem Abwurfwinkel man eine maximale Wurfweite erreicht. Wenn man zu flach abwirft, ist die vertikale Komponente der Abwurfgeschwindigkeit v0 y klein und damit die Wurfdauer kurz. Damit hat der Körper wenig Zeit für seine Horizontalbewegung und die Wurfweite ist kurz. Wenn man andererseits zu steil abwirft, ist die horizontale Komponente der Abwurfgeschwindigkeit v0 x klein und trotz längerer Wurfdauer ergibt sich wegen der kleinen Horizontalgeschwindigkeit ebenfalls eine kurze Wurfweite. Für einen Abwurf vom Erdboden ( y0 =0) ergibt sich die maximale Wurfweite bei einem Abwurfwinkel von α=45 ∘ . Dies kann man auch aus obiger Formel für x ges schnell ableiten. Bei y0 =0 gilt:
 
x ges = 2  v0 x v0 y g ​ = 2  v0 2 g  sinα cosα ​ = v0 2 g  sin(2α) ,
 
wobei das Additionstheorem sin(2φ)=2sinφcosφ aus der Trigonometrie verwendet wurde. Die Funktion sin(2α) nimmt ihren maximalen Wert 1 das erste Mal bei α=45 ∘ an. Daher ist dies der Abwurfwinkel für die größte Wurfweite.

Für Abwürfe von erhöhter Position ( y0 >0) liegt der optimale Abwurfwinkel bei kleineren Winkeln, wie man leicht mit Hilfe der obigen interaktiven Skizze nachprüfen kann.






Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie g=9,81  m s2  .