5.3.5 Wechselstromwiderstände
Video 10: Ohmscher Widerstand im Wechselstromkreis (C)
.
Ohmscher Widerstand (*)
Wird an einen rein ohmschen Widerstand eine Wechselspannung
angelegt, so erzeugt dies einen Strom
der sich phasengleich mit der angelegten Spannung ändert. Für die Beziehung zwischen Strom und Spannung gilt weiterhin das ohmsche Gesetz (sowohl für die Effektivwerte als auch für die Amplituden). Der Wechselstromwiderstand (Impedanz) ist also gleich dem Widerstand, der im Fall des Gleichstroms gilt:
Video 11: Kondensator im Wechselstromkreis (C)
.
Kapazitiver Widerstand (Kondensator) (*)
Legt man an einem Kondensator die Wechselspannung an, so ergibt sich der Strom als die zeitliche Ableitung der Ladung auf dem Kondensator:
Es ergibt sich ebenfalls eine sinusförmige Schwingung, allerdings um phasenverschoben:
Der Strom läuft der Spannung um voraus.
Das Verhältnis zwischen Effektivspannung und Effektivstrom ist das gleiche wie zwischen der Spannungsamplitude und der Stromamplitude . Es wird als kapazitiver Blindwiderstand bezeichnet. Damit wird der Wechselstromwiderstand des Kondensators
Der Blindwiderstand des Kondensators ist umgekehrt proportional zur Frequenz. Er sinkt also bei steigender Frequenz und umgekehrt.
Video 12: Spule im Wechselstromkreis (C)
.
Induktiver Widerstand (Spule) (*)
Wird an eine Spule eine Spannung angelegt, so stellt sich in ihr ein Strom ein, so dass die Selbstinduktionsspannung gerade die äußere Spannung aufhebt:
Ein Strom mit der zeitlichen Abhängigkeit
erfüllt die obige Bedingung, wie man leicht durch Ableiten zeigen kann. Der Strom läuft der Spannung um hinterher.
Auch hier ist das Verhältnis zwischen Effektivspannung und Effektivstrom das gleiche wie zwischen der Spannungsamplitude und der Stromamplitude. Dieses wird als induktiver Blindwiderstand bezeichnet:
Der Blindwiderstand der Spule ist proportional zur Frequenz.
Es zeigt sich also, dass das Vorauseilen bzw. Hinterherhinken des Stroms bei Spule und Kondensator genau gegensätzlich ist.
Zeigerdiagramme (*)
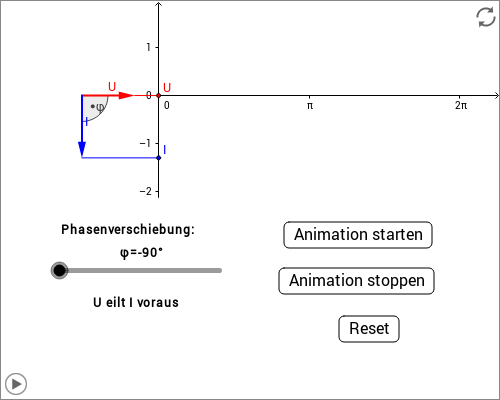
Bei der Berechnung von Wechselstromschaltungen werden zur Erklärung sogenannte Zeigerdiagramme verwendet. Dabei stellen rotierende Zeiger die Spannung und Stromstärke dar. Die -Komponente der Zeiger wird jeweils in Abhängigkeit der Zeit in ein -- bzw. --Diagramm eingetragen. In der folgenden Animation ist ein solches Zeigerdiagramm zu sehen. Über den Schieberegler kann die Phasenverschiebung zwischen Strom und Spannung eingestellt werden. Dabei bedeutet eine Phasenverschiebung von , dass der Strom der Spannung um eine Viertelperiode vorauseilt.
Video 13: Blindleistung im Wechselstromkreis (C)
.
Elektrische Leistung (*)
Eine Wechselspannung erzeugt an einem ohmschen Widerstand einen gleichphasigen Wechselstrom . Die am ohmschen Widerstand verbrauchte elektrische Leistung ist
Der zeitliche Mittelwert ist
Man nennt dies auch die Wirkleistung.
Eine Wechselspannung erzeugt an einem Kondensator den Wechselstrom . Berechnet man das Produkt aus Momentanspannung und Momentanstrom , so erhält man
Der zeitliche Mittelwert dieser Funktion verschwindet, da die Sinus-Funktion um null oszilliert. Dies bedeutet, die Wirkleistung ist null. Dennoch wird am Kondensator steht ein Feld auf und wieder abgebaut. Die zum Aufbauen benötigte Leistung wird zunächst dem Netz entzogen und beim Abbau wieder an das Netz abgegeben. Zur Charakterisierung dieser Größe führt man die Blindleistung des Kondensators ein:
Legt man eine Wechselspannung an einen Kondensator an, so nimmt er Energie während einer Viertelperiode auf und gibt sie in der darauf folgenden wieder ab. Es wird also netto keine elektrische Energie verbraucht. Ein idealer Kondensator hat daher keine Wirkleistung, sondern nur eine Blindleistung.
Auch bei einer Spule liegt eine Phasenverschiebung von zwischen Spannung und Strom vor. Im Zeigerdiagramm stehen Spannung und Strom senkrecht aufeinander. Die ideale Spule (mit verschwindendem ohmschen Widerstand) hat also auch keine Wirkleistung und besitzt ebenfalls die Blindleistung
Eine reale Spule kann als Hintereinanderschaltung einer idealen Spule und eines ohmschen Widerstands angesehen werden. Für das gesamte Bauteil ergibt sich dann eine Phasendifferenz von Spannung und Strom, die zwischen den Werten (ideale Spule) und (rein ohmscher Widerstand) liegt. Als Wirkleistung ergibt sich bei einer Phasendifferenz von :
Für die Blindleistung erhält man allgemein .
Reihenschaltung von Wechselstromwiderständen (*)
Video 14: Reihenschaltung von Wechselstromwiderständen (C)
.
In folgender Skizze sind ein ohmscher Widerstand, eine Spule und ein Kondensator in Reihe geschaltet und an eine äußere Wechselspannungsquelle angeschlossen.
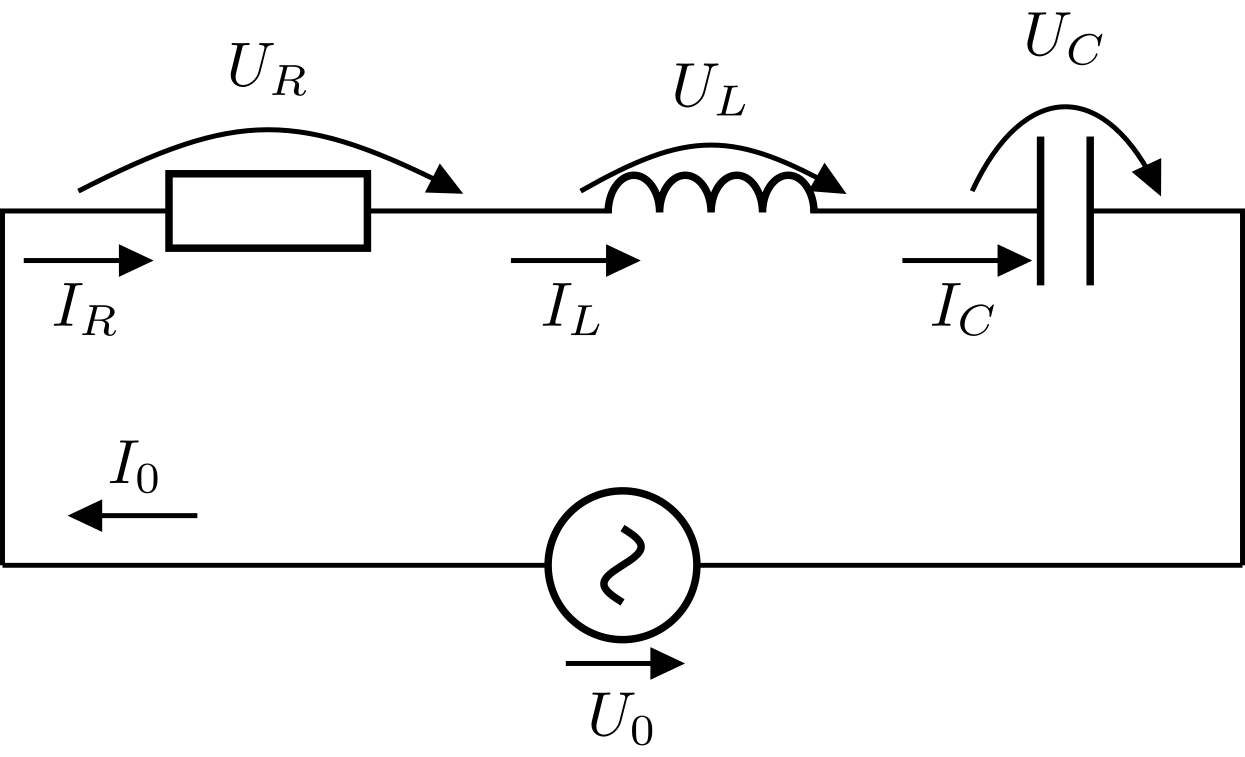
Gemäß der Knotenregel ist der Strom in allen Bauelementen gleich und zwar zu jedem Zeitpunkt. Es gilt also:
Auf Grund der Maschenregel ist die von außen anliegende Wechselspannung entgegengesetzt gleich der Summe der Einzelspannungen an den Bauelementen:
Nun muss man noch berücksichtigen, dass nur beim ohmschen Widerstand die Spannung gleichphasig zum Strom liegt. Dem gegenüber läuft die Spannung an der Spule dem Strom um voraus, während die Spannung am Kondensator dem Strom um hinterher läuft. Dies ist im Zeigerdiagramm der folgenden Skizze veranschaulicht.

Die obige Skizze zeigt eine Momentaufnahme eines Zeigerdiagramms. Durch vektorielle Addition der Spannungszeiger kann die Amplitude der Gesamtspannung berechnet werden. Man erhält für die gesamte Spannungsamplitude :
Für die Impedanz der Gesamtschaltung erhält man dann:
Die Phasendifferenz ergibt sich mit:
Parallelschaltung von Wechselstromwiderständen (*)

Abbildung 5.3.157: Reihenschaltung von Widerstand, Spule und Kondensator (C)
Gemäß der Knotenregel ist der Strom in allen Bauelementen gleich und zwar zu jedem Zeitpunkt. Es gilt also:
Auf Grund der Maschenregel ist die von außen anliegende Wechselspannung entgegengesetzt gleich der Summe der Einzelspannungen an den Bauelementen:
Nun muss man noch berücksichtigen, dass nur beim ohmschen Widerstand die Spannung gleichphasig zum Strom liegt. Dem gegenüber läuft die Spannung an der Spule dem Strom um voraus, während die Spannung am Kondensator dem Strom um hinterher läuft. Dies ist im Zeigerdiagramm der folgenden Skizze veranschaulicht.

Abbildung 5.3.158: Zeigerdiagramm (C)
Die obige Skizze zeigt eine Momentaufnahme eines Zeigerdiagramms. Durch vektorielle Addition der Spannungszeiger kann die Amplitude der Gesamtspannung berechnet werden. Man erhält für die gesamte Spannungsamplitude :
Für die Impedanz der Gesamtschaltung erhält man dann:
Die Phasendifferenz ergibt sich mit:
Parallelschaltung von Wechselstromwiderständen (*)
Video 15: Parallelschaltung von Wechselstromwiderständen (C)
.
In der folgenden Skizze sind ein ohmscher Widerstand, eine Spule und ein Kondensator parallel zu einer äußeren Wechselspannungsquelle geschaltet.
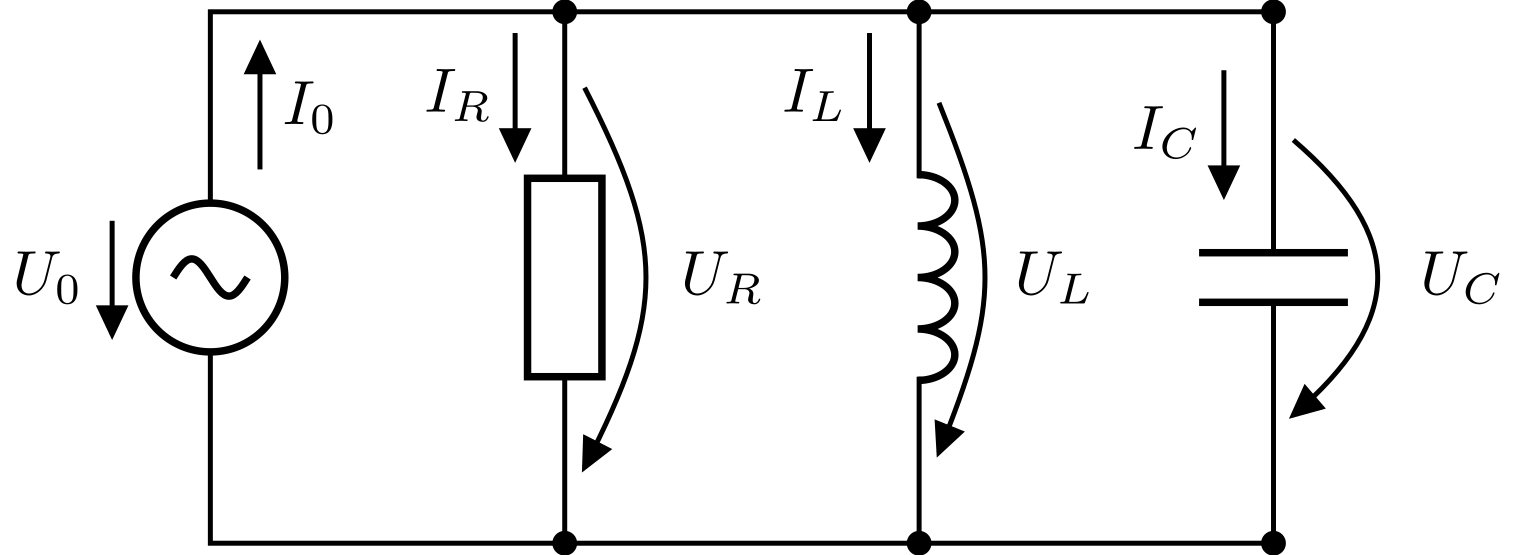
Nun fällt hier über alle drei Bauteile zu jedem Zeitpunkt die gleiche Spannung ab, die gleich der von außen angelegten Spannung ist:
Gemäß der Knotenregel addieren sich die Ströme durch die einzelnen Bauteile zum Gesamtstrom :
Nun muss man wieder berücksichtigen, dass die verschiedenen Ströme , und eine unterschiedliche Phasendifferenz zur Momentanspannung besitzen. Dies ist im Zeigerdiagramm der folgenden Skizze veranschaulicht.

Die obige Skizze zeigt eine Momentaufnahme eines Zeigerdiagramms. Durch vektorielle Addition der Stromzeiger kann die Amplitude des Gesamtstroms berechnet werden. Man erhält für die gesamte Stromamplitude :
Für die Impedanz der Gesamtschaltung erhält man dann:
Die Phasendifferenz ergibt sich mit:

Abbildung 5.3.159: Parallelschaltung von Widerstand, Spule und Kondensator (C)
Nun fällt hier über alle drei Bauteile zu jedem Zeitpunkt die gleiche Spannung ab, die gleich der von außen angelegten Spannung ist:
Gemäß der Knotenregel addieren sich die Ströme durch die einzelnen Bauteile zum Gesamtstrom :
Nun muss man wieder berücksichtigen, dass die verschiedenen Ströme , und eine unterschiedliche Phasendifferenz zur Momentanspannung besitzen. Dies ist im Zeigerdiagramm der folgenden Skizze veranschaulicht.

Abbildung 5.3.160: Zeigerdiagramm (C)
Die obige Skizze zeigt eine Momentaufnahme eines Zeigerdiagramms. Durch vektorielle Addition der Stromzeiger kann die Amplitude des Gesamtstroms berechnet werden. Man erhält für die gesamte Stromamplitude :
Für die Impedanz der Gesamtschaltung erhält man dann:
Die Phasendifferenz ergibt sich mit:
Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.

