4.6.2 Gedämpfte Schwingungen

Noch kein Basiswissen vorhanden ...
Zu diesem Abschnitt gibt es leider noch kein Basiswissen.

Video 17: Gedämpfte Schwingungen (C) .

Nach der Untersuchung des idealisierten Modells ohne dämpfende Reibung soll nun ein realistischeres Modell mit Reibung untersucht werden. Für einen einfachen Fall wird die Lösung angegeben.

Im Allgemeinen kann der Ausdruck für die Reibung kompliziert sein. Ein einfacher Fall ist, dass die Reibungskraft vom Betrag konstant ist und stets entgegen der Geschwindigkeit gerichtet ist (s. Amontonssche Gesetze). Hier soll ein anderer einfacher Fall betrachtet werden, nämlich dass die Reibungskraft entgegengesetzt und proportional der Geschwindigkeit ist. In mechanischen Systemen tritt dieser Fall auf, wenn ein Gegenstand langsam durch ein zähes Fluid bewegt wird und die Zähigkeit unabhängig von der Bewegungsgeschwindigkeit ist (s. Newtonsches Fluid und Reynolds-Zahl).

Mit einer positiven Konstante

c

können wir für den Reibungsterm also

- c \cdot v = - c \cdot \overset{\cdot}{x}

schreiben.

Die Bewegungsgleichung für den Oszillator (hier eine Feder) mit geschwindigkeitsproportionaler Dämpfung lautet

%\MLabel{Physik_Schwingungen_EQHONewtonD} m~ \ddot{x} = -D~x -c~ \dot{x} .

Division durch die Masse führt mit der Definition

c = m \cdot γ

auf

\ddot{x} = - \gamma ~ \dot{x} - \omega_0^2~x . \MLabel{SCHWINGUNGEN_GEDAEMPFT_EQHOD}

Im Vergleich zur freien harmonischen Schwingung ist ein linearer Term mit der Ableitung erster Ordnung hinzugekommen. Dies ändert nichts am Typ der Differentialgleichung (gewöhnliche explizite lineare homogene Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten), auch wenn die Lösung komplexer wird und schlecht geraten werden kann. Hier führt folgender Ansatz zum Ziel:

x (t) = \exp (λ t), λ \in ℂ

.
Einsetzen in Gl. (4.6.1) und Kürzen von

\exp (λ t)

führt auf die Bestimmungsgleichung

\lambda^2 + \gamma \lambda + \omega_0^2 = 0

für

λ

mit den Lösungen

\lambda_{1/2} = -\frac{\gamma}{2} \pm \MIU \sqrt{\omega_0^2-\left(\frac{\gamma}{2}\right)^2}.

falls

ω_{0}^{2} > {(\frac{γ}{2})}^{2}

. Mit der Abkürzung

ω_{d} = \sqrt{ω_{0}^{2} - {(\frac{γ}{2})}^{2}}

lautet die allgemeine Lösung

x (t) = A_{1} \exp (- \frac{γ}{2} t) \exp (i ω_{d} t)

​ + A_{2} \exp (- \frac{γ}{2} t) \exp (- i ω_{d} t) .

mit

A_{1}, A_{2} \in ℂ

. Damit die Lösungen wie erforderlich reell sind, müssen

A_{1}

und

A_{2}

zueinander komplex konjugiert sein. Unter Verwendung der Eulerformel und der Additionstheoreme ergeben sich drei Schreibweisen, analog zum Fall ohne Dämpfung.

Die Gleichung kann verhältnismäßig einfach gelöst werden, wenn komplexe Zahlen verwendet werden (s. Bemerkung). Da komplexe Zahlen aber über den Inhalt dieses Kurses hinaus führen, wird hier die allgemeine Lösung ohne Herleitung angegeben:

Die allgemeine Lösung von Gl. (4.6.1) kann mit folgenden Schreibweisen angegeben werden:

x_{\text{h}}(t) &=& \displaystyle x_{\text{max}}\exp\left(-\Mtfrac{\gamma}{2}t\right)\cos\left(\omega_{\text{d}} (t-t_1)\right)\MLabel{SCHWINGUNGEN_GEDAEMPFT_EQHODDLOES1}

oder

x_{\text{h}}(t) &=& \displaystyle x_{\text{max}}\exp\left(-\Mtfrac{\gamma}{2}t\right)\cos(\omega_{\text{d}} t+\Mvarphi_{\text{d}})\MLabel{SCHWINGUNGEN_GEDAEMPFT_EQHODDLOES2}

oder

x_{\text{h}}(t) &=& \displaystyle \exp\left(-\Mtfrac{\gamma}{2}t\right)\left(A\cos\left(\omega_{\text{d}} t\right)+B\sin\left(\omega_{\text{d}} t\right)\right)\MLabel{SCHWINGUNGEN_GEDAEMPFT_EQHODDLOES3}%\MLabel{Physik_Schwingungen_EQHODLoes3}

mit

\omega_{\text{d}} = \sqrt{\omega_0^2-\left(\frac{\gamma}{2}\right)^2} \MLabel{SCHWINGUNGEN_GEDAEMPFT_EQOmegaD}

(4.6.5)

in Gleichung (4.6.4) gilt

x_{max} = \sqrt{A^{2} + B^{2}}

.

Man unterscheidet drei Fälle:

Schwingfall $ω_{0} > \frac{γ}{2}$ (schwache oder unterkritische Dämpfung)
Skizze: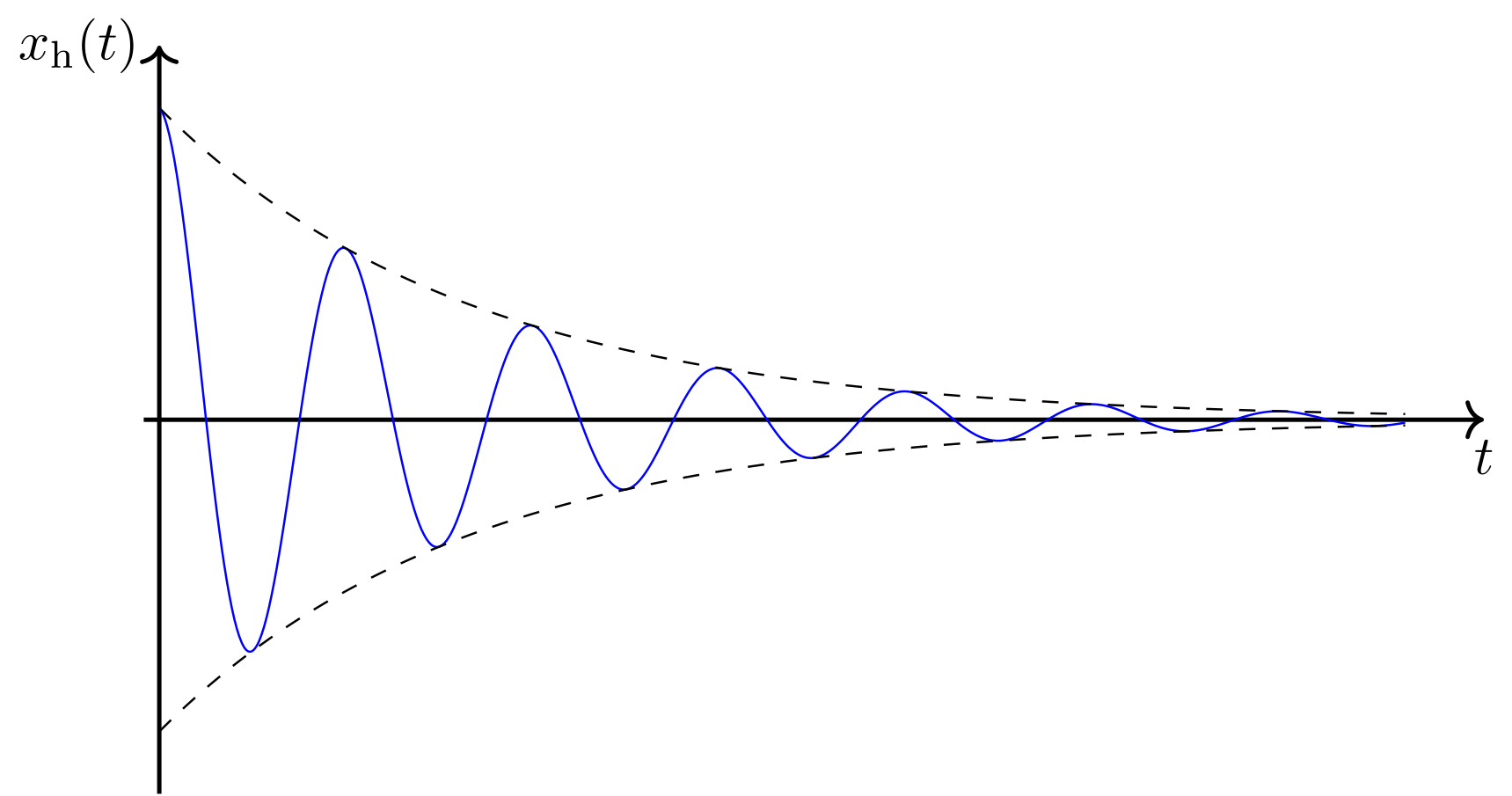

Abbildung 4.6.75: Schwache Dämpfung (C)
Aperiodischer Grenzfall $ω_{0} = \frac{γ}{2}$ (kritische Dämpfung)
Skizze: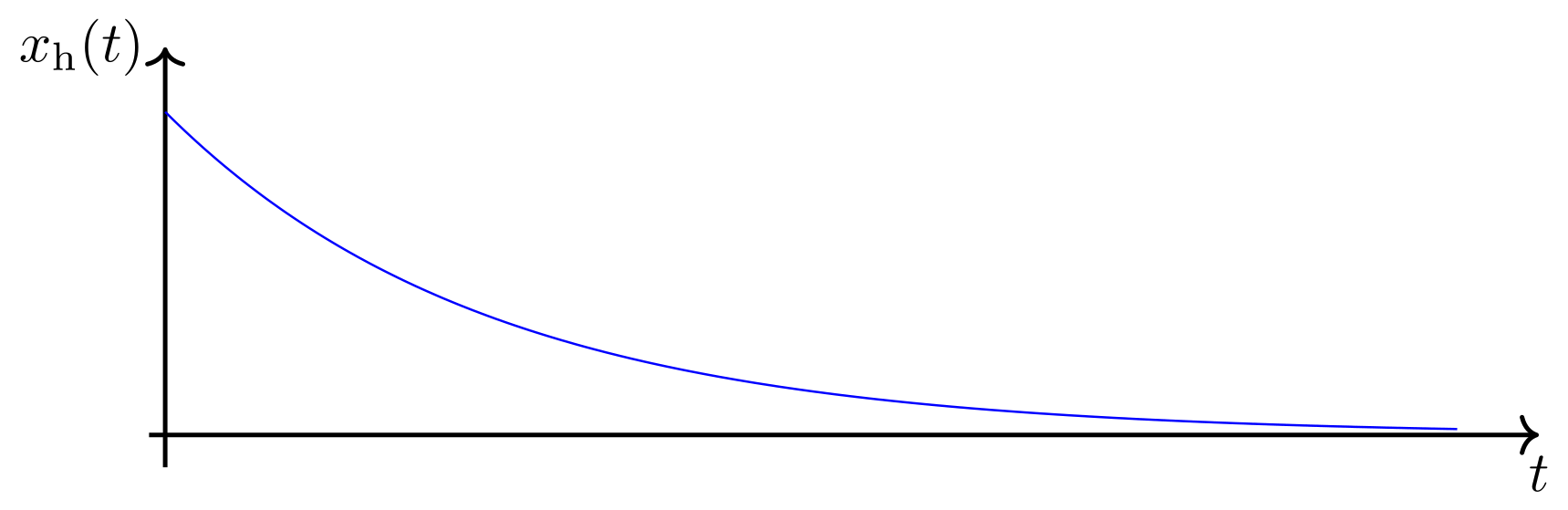

Abbildung 4.6.76: Kritische Dämpfung (C)
Kriechfall $ω_{0} < \frac{γ}{2}$ (starke oder überkritische Dämpfung)
Skizze:

Abbildung 4.6.77: Starke Dämpfung (C)

In einigen Quellen ist in Gleichungen (4.6.2)–(4.6.4) für die Dämpfung nur der Faktor

\exp (- γ t)

zu finden. Dementsprechend wird in diesen Quellen bei der Bewegungsgleichung (4.6.1) für die Proportionalitätskonstante

2 γ

statt

γ

eingesetzt. Bei dieser Definition sind natürlich auch die daraus folgenden Gleichungen entsprechend anzupassen.

Als Folge der geschwindigkeitsproportionalen Reibung wird die Oszillation exponentiell gedämpft und die Oszillationsfrequenz wird verringert. Die Lösung ist in den Gleichungen (4.6.2)–(4.6.4) mit dem Index

h

versehen, da sie in der Mathematik als homogene Lösung bezeichnet wird. Im Abschnitt über erzwungene Schwingungen wird die homogene Lösung als Einschwingvorgang in Erscheinung treten.

Online-Brückenkurs Physik

1 Allgemeines

2 Eingangstests

3 Grundlagen

4 Mechanik

5 Elektromagnetismus

6 Optik

7 Wärmelehre

8 Wellen

Kursinformationen

Legende

4.6.2 Gedämpfte Schwingungen