2. Mechanik
  3. Arbeit und Energie
  4. Energieerhaltung (!),(+)

4.3.2 Energieerhaltung





 

Noch kein Basiswissen vorhanden ...
Zu diesem Abschnitt gibt es leider noch kein Basiswissen.

Video 14: Abgeschlossene Systeme (C) .



Als Energie bezeichnet man die Fähigkeit eines Systems, Arbeit nach außen abgeben zu können. Energie ist in diesem Sinne also gespeicherte Arbeit.


Wir betrachten ein System, das räumlich begrenzt ist und bei dem kein Austausch von Materie oder Energie mit der Außenwelt erfolgt. Solch ein System nennt man ein abgeschlossenes System. Eine wichtige Eigenschaft eines abgeschlossenen Systems ist die Erhaltung der Energie. Die Energie verringert und vermehrt sich in diesem System nicht. Sie kann aber zwischen verschiedenen Energieformen umgewandelt werden. Im Folgenden betrachten wir einige wichtige Energieformen.

 

Kinetische Energie (!)


Video 15: Kinetische Energie (C) .



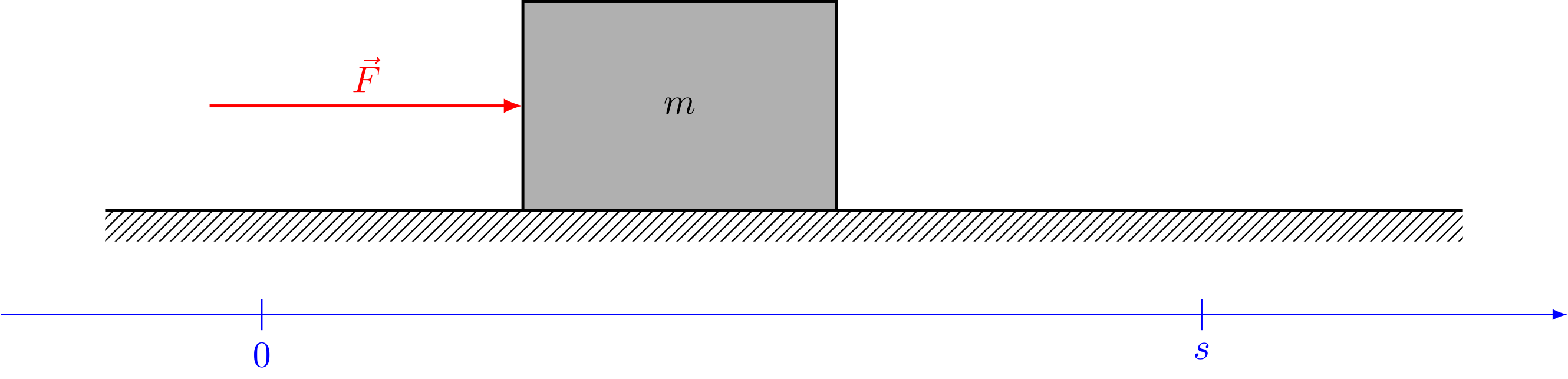
./_85C0005C_4x.png
Abbildung 4.3.34: Körper wird aus der Ruhe beschleunigt  (C)

Beschleunigt man einen Körper durch eine äußere Kraft, so erhöht sich seine Geschwindigkeit. Ist diese beschleunigende Kraft konstant, so kann man leicht die Arbeit berechnen, die benötigt wird, um ihn aus der Ruhe auf die Geschwindigkeit v zu beschleunigen. Man erhält:
 
W=F s ​ =ma s=ma  v2 2a ​ = 1 2 m v2 = E kin  .
 
Dabei haben wir die für gleichmäßig beschleunigte Bewegungen geltende Beziehung s= v2 2a aus Abschnitt 4.2.2 verwendet.

Die während der Beschleunigung am Körper geleistete Arbeit kann wegen der Energieerhaltung nicht verloren gehen. Sie ist daher als kinetische Energie E kin in der Bewegung des Körpers gespeichert.
Man definiert daher die kinetische Energie eines Körpers als:

E kin = 1 2 m v2  .



 

Potentielle Energie (!)


Video 16: Potentielle Energie (Lageenergie) (C) .



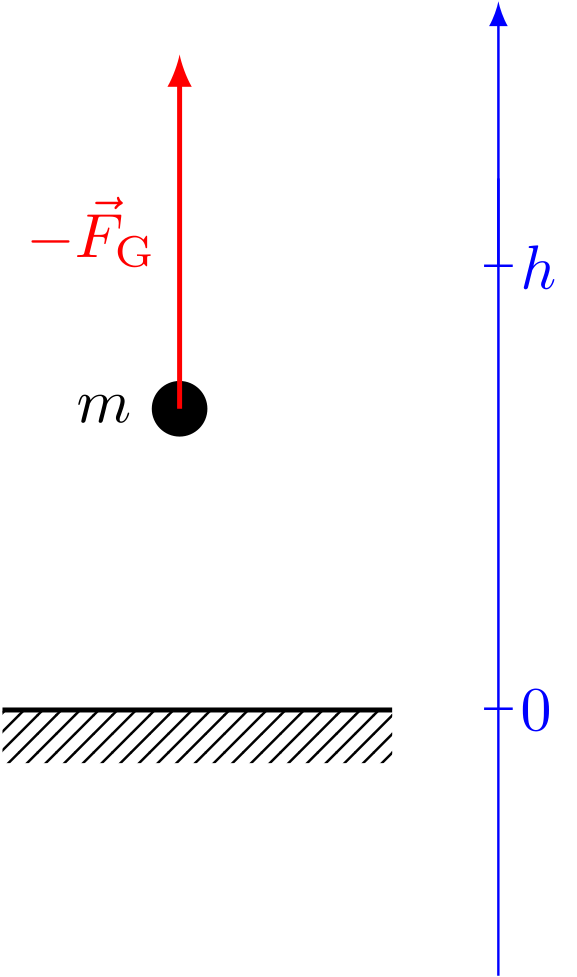
./_06D59AB4_4x.png
Abbildung 4.3.35: Potentielle Energie  (C)



Die potentielle Energie eines Körpers ist ein Maß für die Möglichkeit des Körpers, aufgrund seiner Lage Arbeit zu verrichten. Deshalb spricht man auch von Lageenergie. Sie ist die Energie, mit der man einen Körper anhebt und dabei gegen seine Gewichtskraft Arbeit verrichtet,

W= F G  h=mgh= E pot  .

Kehrt der Körper in die Ausgangslage zurück, so wird die hineingesteckte Arbeit wieder frei. Diese gespeicherte Arbeit nennt man die potentielle Energie des Körpers.

Man kann zeigen, dass die Arbeit, die benötigt wird, um einen Körper anzuheben, nur vom Anfangs- und Endpunkt der Bewegung abhängt, jedoch nicht von dem zurückgelegten Weg. Bei einer solchen Wegunabhängigkeit spricht man auch von einer konservativen Kraft.
Die zu leistende Arbeit und damit auch die potentielle Energie, die beim Anheben eines Körpers in diesen gesteckt wird, kann daher auch bei beliebigen Wegen immer berechnet werden als

E pot =mgh .



Video 17: Beispiel zur Lageenergie (C) .



Beispiel 4.3.16  
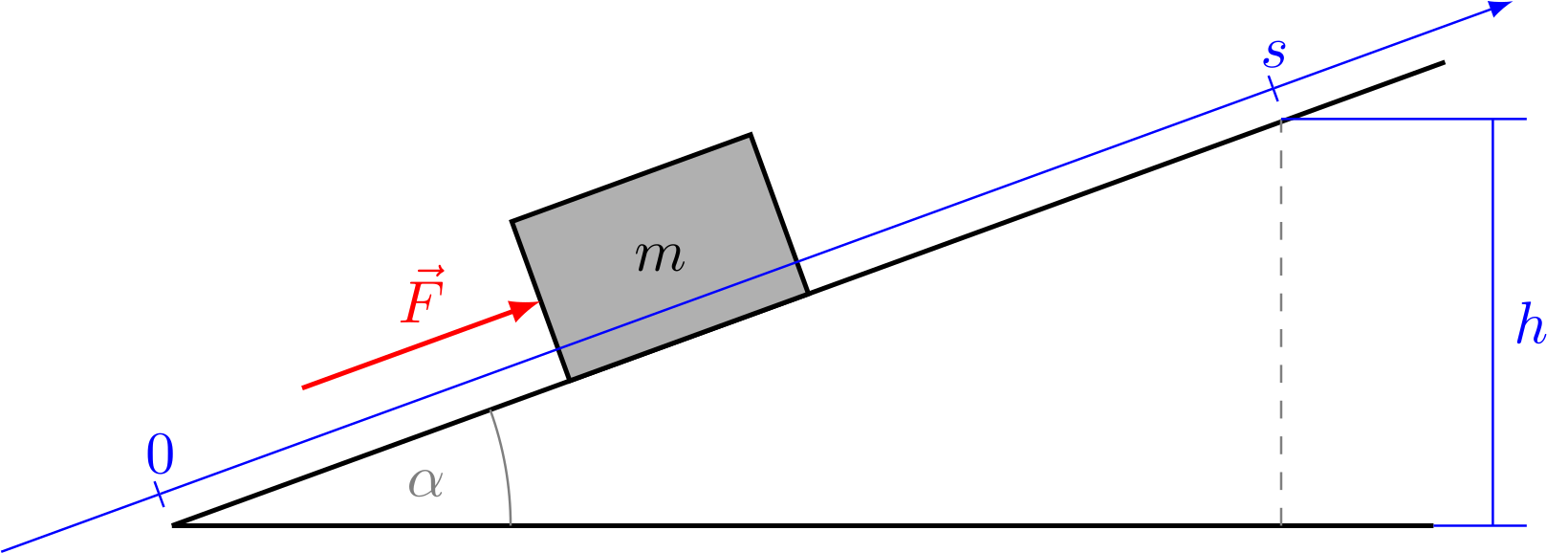
./_C284606E_4x.png
Abbildung 4.3.36: Körper auf schiefer Ebene  (C)

Schiebt man einen Körper mit konstanter Geschwindigkeit und reibungsfrei entlang einer schiefen Ebene, die den Winkel α zur Horizontalen aufweist, auf die Höhe h, so muss man Arbeit nur gegen die Hangabtriebskraft F H verrichten, die kleiner als die Gewichtskraft des Körpers ist:

F H = F G  sinα .

Im Gegenzug muss die dafür erforderliche Kraft F aber über die gesamte Streckenlänge s der schiefen Ebene angewendet werden:

s= h sin(α)



Die aufzuwendende Arbeit ist das Produkt aus der Kraft, die entlang eines Weges wirkt, und der Länge der Wegstrecke. In diesem Beispiel ist die wirkende Kraft im Betrag gleich groß wie die Hangabtriebskraft und wirkt entlang der Wegstrecke s. Insgesamt erhält man als Gesamtarbeit und damit als potentielle Energie wieder das gleiche Ergebnis:
 
W= E pot =F·s ​ = F G sinα· h sinα ​ = F G ·h=mgh .
 
Die potentielle Energie hängt also im Endergebnis nur von der Gewichtskraft und der Höhe des Körpers ab, nicht aber von der Wahl des zurückgelegten Weges.


Video 18: Potentielle Energie einer Feder (Federenergie) (C) .



./_303055D9_4x.png
Abbildung 4.3.37: Zur Erläuterung der Federenergie  (C)

Potentielle Energie entsteht auch bei der Dehnung oder Stauchung elastischer Körper. Je stärker eine Feder gespannt oder gestaucht ist, umso größer ist die Entfernung s des Feder-Endpunktes zu seiner Ruhelage (= Ausgangsposition im entspannten Fall) und umso mehr Arbeit kann die Feder leisten, um die Ruhelage wieder zu erreichen. Die Kraft, die zur Dehnung der Feder erforderlich ist, beträgt nach dem hookeschen Gesetz:

F=D s .



Da diese Kraft nicht konstant ist, sondern sich während der Dehnung der Feder ändert, erhält man die Arbeit über das Wegintegral:
 
W= ∫0 s F( s' ) d s' ​ = ∫0 s D s'  d s' = 1 2 D s2  .
 
In der Feder ist demnach die potentielle Energie

E pot = 1 2 D s2

gespeichert, die auch Spannenergie genannt wird.
Wenn man die Feder wieder loslässt, kann man sie wieder freisetzen. Sie wird dann in andere Energieformen (z.B. kinetische Energie) umgewandelt.

 

Energieerhaltungssatz (!)


Video 19: Energieerhaltungssatz (C) .



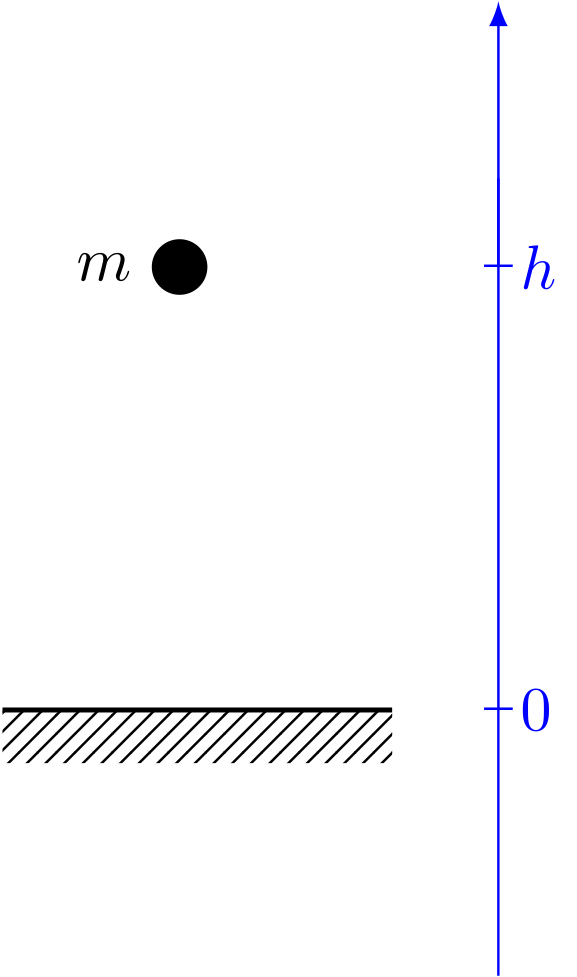
./_4157DD94_4x.png
Abbildung 4.3.38: Energieerhaltungsgesetz  (C)

Betrachten Sie einen fallenden Körper. Seine Gewichtskraft leistet über die Fallstrecke hinweg eine beschleunigende Arbeit. Diese vom Körper geleistete beschleunigende Arbeit entspricht dabei genau seinem Verlust an potentieller Energie. Andererseits erzeugt diese Arbeit über die Beschleunigung kinetische Energie.
Insgesamt bleibt die Gesamtenergie, also die Summe aus potentieller und kinetischer Energie gleich. Mathematisch wird dieser Zusammenhang folgendermaßen formuliert, wobei das Delta Δ für die Änderung zwischen den beiden Zuständen steht:

-Δ E pot = W=Δ E kin ⟺  Δ E pot +Δ E kin = 0 ⟺   E pot + E kin =E = const  .

Dies ist der Energieerhaltungssatz für mechanische Energie ohne Reibungsverluste.


Video 20: Beispiel zum Energieerhaltungssatz (C) .



Beispiel 4.3.17  
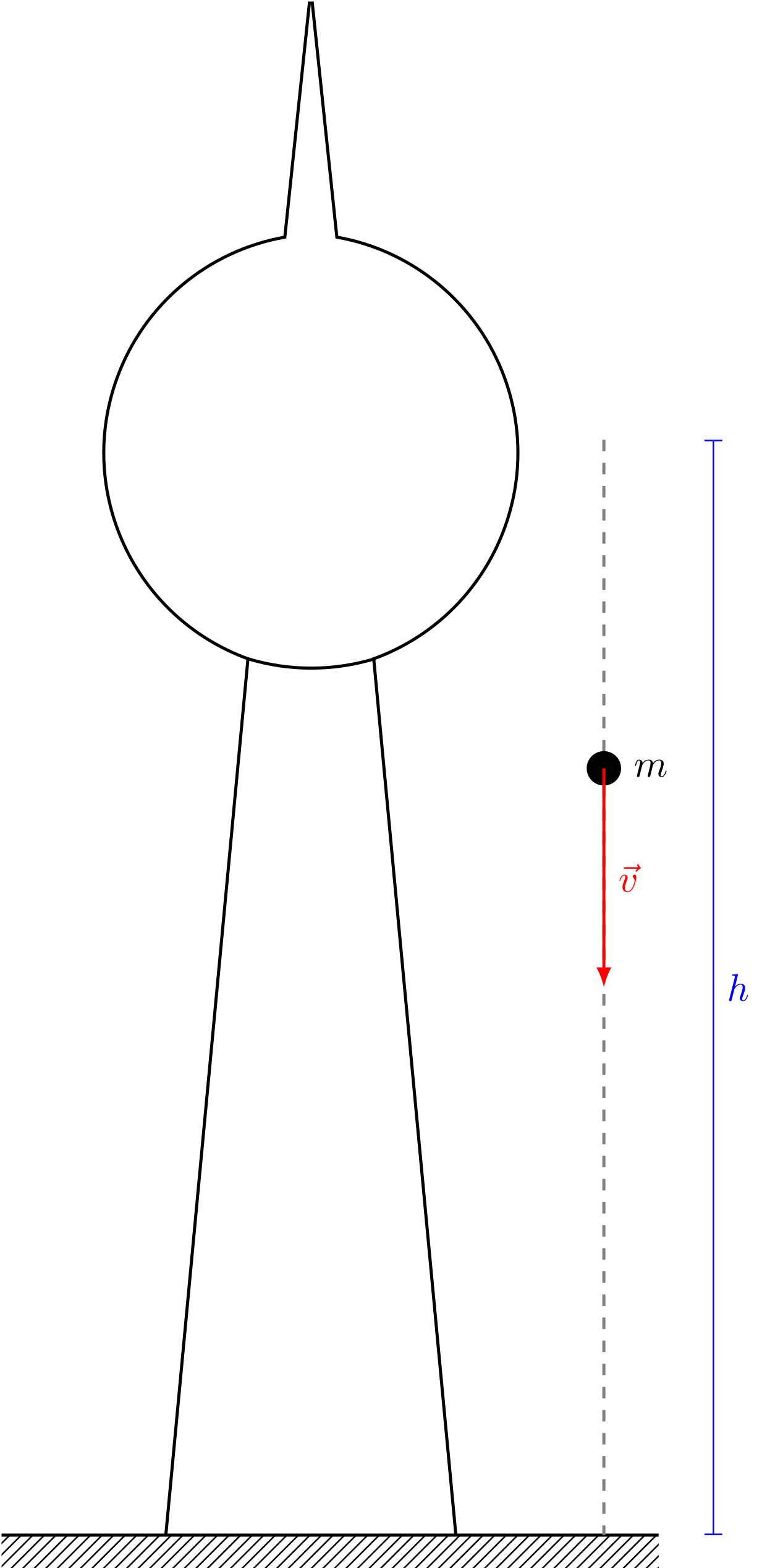
./_16F67E4F_4x.png
Abbildung 4.3.39: Kamera fällt vom Berliner Fernsehturm  (C)



Bei einem Versuch, die Stadt Berlin von oben zu fotografieren, fällt einem Fotografen auf dem Berliner Fernsehturm in einer Höhe von h=203,78 m seine Kamera aus der Hand. In der Hand des Fotografen befindet sich die Kamera in Ruhe.

Mit welcher Geschwindigkeit fällt die Kamera kurz vor dem Aufprall am Boden, wenn Luftreibung vernachlässigt wird?



Video 21: Beispiel zum Energieerhaltungssatz (C) .



Beispiel 4.3.18  
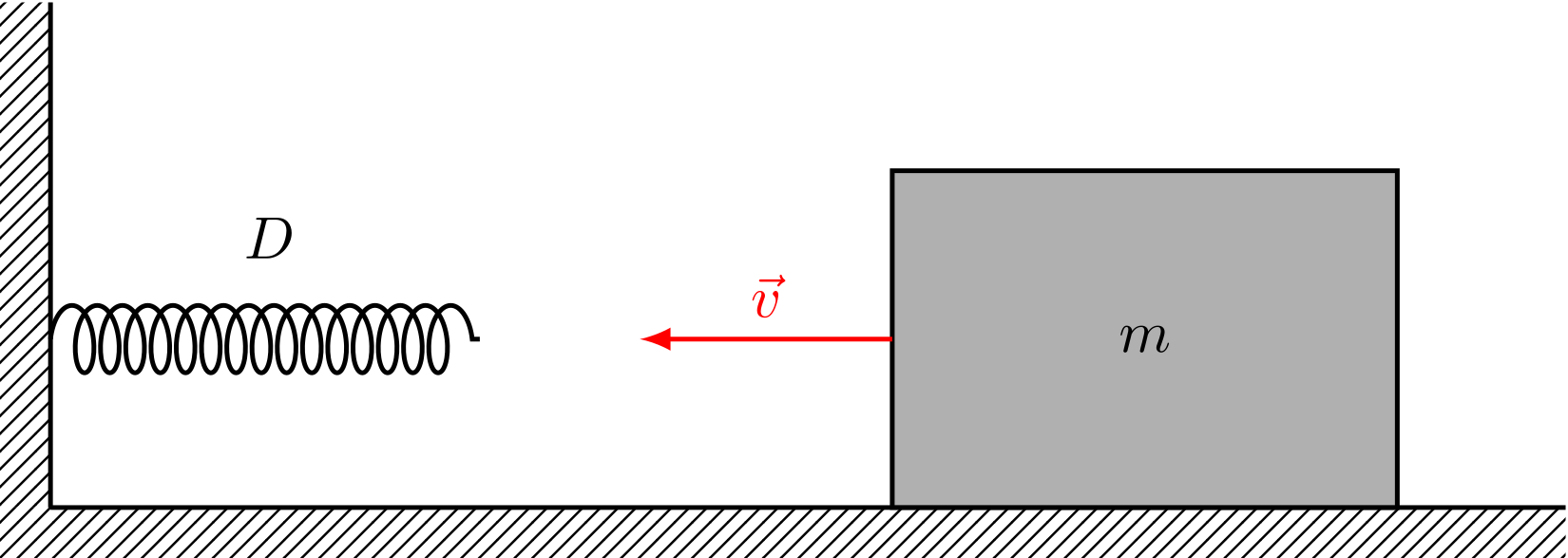
./_F535D8D7_4x.png
Abbildung 4.3.40: Feder bremst Körper  (C)



Ein Quader der Masse m=0,5 kg rutscht reibungsfrei horizontal mit einer Geschwindigkeit des Betrags v=2 m/s gegen eine an einer Wand angebrachte Feder der Federhärte D=5000 N/m.
  1. Um welche Strecke s wird die Feder gestaucht, bis der Quader vollständig zum Stillstand kommt?

  2. Wie verhält sich das System nach dem vollständigen Stillstand des Quaders?



 

Wärmeenergie (+)


Video 22: Wärmeenergie (C) .



./_C6D9F777_4x.png
Abbildung 4.3.41: Bewegter Körper auf rauem Untergrund  (C)

Wärmeenergie wird z.B. dann freigesetzt, wenn Reibungsarbeit geleistet wird. Wird ein Körper gegen eine konstante Reibungskraft gezogen, so wird Reibungsarbeit verrichtet:

W= F R  s=Q .

Die Wärmeenergie Q ist eine Energieform mit einer speziellen Eigenschaft. Alle anderen anderen Energieformen können ineinander umgewandelt werden. Man kann sie auch in Wärmeenergie umwandeln. Allerdings lässt sich die Wärmeenergie selbst nicht oder nur teilweise in die ursprünglichen Energieformen zurück verwandeln.

Video 23: Beispiel Reibung (C) .



Beispiel 4.3.19  
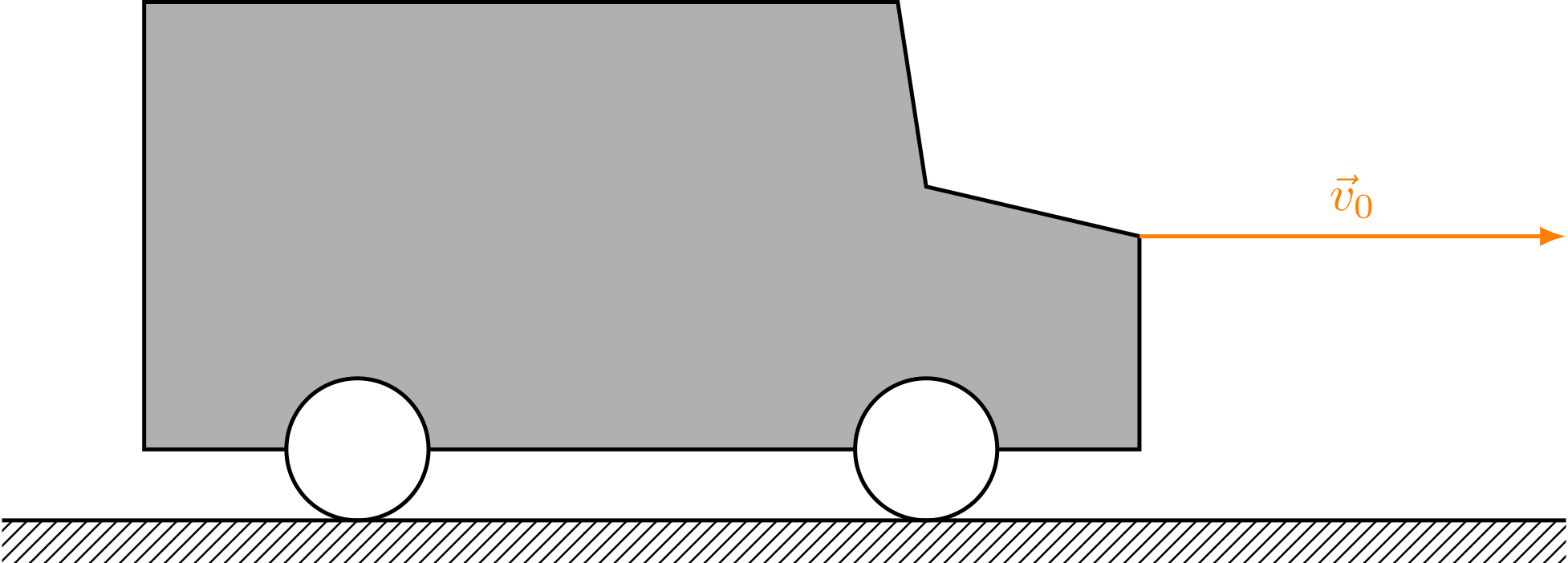
./_5C36DF41_4x.png
Abbildung 4.3.42: Bremsendes Auto  (C)



Ein Auto der Masse m=2500 kg wird auf freier gerader Strecke mit blockierenden Reifen abgebremst. Das Auto bewege sich mit einer Anfangsgeschwindigkeit des Betrags v0 =72 km/h. Zwischen Fahrbahn und Reifen herrsche ein Gleitreibungskoeffizient μ G =0,8.
  1. Bestimmen Sie den Bremsweg des Autos über eine Energiebetrachtung (kinetische Energie, Beschleunigungsarbeit).

  2. Wie groß ist der Bremsweg des Autos, wenn der Reibungskoeffizient sich durch Regen auf μ G =0,2 verringert?





Der Energieerhaltungssatz kann auf alle Energieformen erweitert werden. Er ist ein sehr grundlegendes physikalisches Gesetz. Es kann keine Energie gewonnen oder verloren werden. Die unterschiedlichen Energieformen werden lediglich ineinander umgewandelt.

Durch Anwendung des Energieerhaltungssatzes kann man die Lösung mancher Aufgabenstellungen in der Mechanik stark vereinfachen. Ein Beispiel wäre z.B. ein Körper, der auf einer komplizierten Bahn insgesamt eine Höhendifferenz h durchläuft. Die Aufgabe lautet, die Endgeschwindigkeit des Körpers zu ermitteln. Dies kann man recht einfach erreichen, indem man die potentiellen und kinetischen Energien am Anfang und Ende der Bewegung miteinander vergleicht. Die Einzelheiten der Bewegung auf dem Weg zwischen dem Anfangs- und Endzustand müssen dann gar nicht betrachtet werden.

Mit dem Satz von der Energieerhaltung versteht man das zuvor schon zitierte „Goldene Gesetz der Mechanik“ noch besser:

„Was man an Kraft spart, muss man an Weg zusetzen“ (Wikipedia).


Einen Kraftwandler kann man auch als eine Maschine auffassen. Der Benutzer leistet an der Maschine Arbeit und die Maschine überträgt diese Arbeit an einer anderen Stelle wieder an ein Objekt. Die kraftverstärkende Wirkung der Maschine, wie z.B. eines Hebels oder eines Flaschenzugs, beruht nun auf folgendem Prinzip: Die Wegstrecke s N , entlang der die Kraft F N auf der Seite des Benutzers aufgewendet wird, ist länger ist als die Wegstrecke s O , über die die Maschine die Kraft F O an das Objekt weitergibt. Wegen der Energieerhaltung steht aber fest, dass die an der Maschine geleistete und die von der Maschine erbrachte Arbeit gleich sind. Die Arbeit ergibt sich nun aus dem Produkt von Kraft und Wegstrecke:

F N · s N =W= F O · s O  .

Aus dieser Beziehung folgt sofort, dass die Kraft F N , die der Benutzer aufwendet, um den Faktor s N / s O verstärkt wird, und diese verstärkte Kraft F O auf das Objekt wirkt.



Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie g=9,81  m s2  .