8.2.5 Interferenz und Beugung
Video 6: Interferenz und Beugung von Wasserwellen (C)
.
Im Normalfall gibt es nicht nur eine einzige Quelle, die Wellen aussendet, sondern mehrere unabhängige Quellen, die gleichzeitig phasenverschobene Signale mit verschiedenen Frequenzen und Amplituden aussenden. Das Ergebnis ist eine unsystematische Überlagerung aller Wellen. Wenn die an der Überlagerung beteiligten Wellen völlig unabhängig sind, spricht man von inkohärenten Wellen.
Interferenz (+)
Kohärenz
Für den Spezialfall, dass die sich überlagernden Wellen die gleiche Frequenz und eine konstante Phasenverschiebung relativ zueinander haben, spricht man von kohärenten Wellen.
Interferenz
Bei der Überlagerung von Wellen addieren sich zu jedem Zeitpunkt überall im Ausbreitungsmedium die momentanen Auslenkungen der einzelnen Wellen. Wenn sich kohärente Wellen überlagern, spricht man von Interferenz. Dabei können sich Wellen verstärken (konstruktive Interferenz) oder auch schwächen bzw. im Extremfall völlig auslöschen (destruktive Interferenz). Das dabei entstehende Bild nennt sich Interferenzmuster.
Für den Spezialfall, dass die sich überlagernden Wellen die gleiche Frequenz und eine konstante Phasenverschiebung relativ zueinander haben, spricht man von kohärenten Wellen.
Interferenz
Bei der Überlagerung von Wellen addieren sich zu jedem Zeitpunkt überall im Ausbreitungsmedium die momentanen Auslenkungen der einzelnen Wellen. Wenn sich kohärente Wellen überlagern, spricht man von Interferenz. Dabei können sich Wellen verstärken (konstruktive Interferenz) oder auch schwächen bzw. im Extremfall völlig auslöschen (destruktive Interferenz). Das dabei entstehende Bild nennt sich Interferenzmuster.
Interferenz (+)
Video 7: Interferenz (C)
.
Interferenz tritt auf, wenn Wellenzüge, die aus der gleichen Lichtquelle stammen, zunächst getrennt und dann wieder überlagert werden. Die Auftrennung in die Wellenzüge kann z.B. durch teilweise Reflexion oder Abschattung des Lichts erfolgen. Am Ort der Überlagerung kommen die Wellenzüge im Allgemeinen mit einer unterschiedlichen Phase an, d.h. die Schwingung des einen Wellenzugs ist z.B. schon etwas weiter als die des anderen. Dies wird durch unterschiedliche Wegstrecken der beiden Wellenzüge verursacht. Der eine Wellenzug ist also früher am Ort der Überlagerung als der andere. Wellenberge und Wellentäler der beiden Wellenzüge verschieben sich dadurch gegeneinander. Das Ergebnis dieser Verschiebung wird in der folgenden animierten Skizze illustriert. Es sind zwei Wellenzüge (grün und rot) dargestellt, die am gleichen Ort aufeinander treffen und dabei miteinander interferieren sollen. Das Resultat dieser Interferenz ist die Summe der beiden Wellenzüge und wird darunter als Welle (blau) angezeigt. Zunächst sind die beiden interferierenden Wellenzüge nicht gegeneinander verschoben, Wellenberg und Wellental treffen also jeweils genau aufeinander. Als Amplitude der resultierenden Welle ergibt sich die Summe der Amplituden der Einzelwellen.
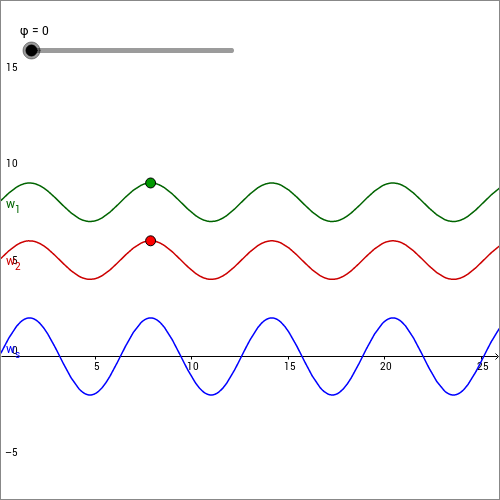
Verschieben Sie nun den Regler für die Phasenverschiebung zwischen den beiden Wellen. Dadurch werden die beiden Wellenzüge in der Phase gegeneinander verschoben. Die Wellenberge und Wellentäler treffen dann nicht mehr genau aufeinander. Die Amplitude der resultierenden Welle wird kleiner und ist dann nicht mehr die Summe der Amplituden der Einzelwellen. Wenn die beiden Wellenzüge genau so gegeneinander verschoben sind, dass Wellenberge auf Wellentäler treffen, d.h. für , heben sich diese sogar genau auf. Als Resultat der Interferenz verschwindet die Amplitude der resultierenden Welle. Die beiden Wellen löschen sich also gegenseitig aus. Vergrößern Sie nun die Phasenverschiebung bis zu einem Wert von , so treffen Wellenberge wieder auf Wellenberge und die Amplitude der resultierenden Welle ist wieder maximal.
Interferenz von Licht an einer dünnen Schicht (*)
Video 8: Interferenz an einer dünnen Schicht (C)
.
Als erstes Beispiel für die Interferenz von Licht soll die Reflexion einer Lichtwelle an einer dünnen Schicht betrachtet werden. Ein bekanntes Beispiel aus dem Alltag sind Wasserflächen, die von einer dünnen Ölschicht bedeckt werden. Diese Schichten sind meist so dünn, dass ihre Dicke der Größenordnung der Wellenlänge des Lichts entspricht. Zur Interferenz kommt es nun dadurch, dass ein Teil des Lichts direkt an der Oberfläche der Ölschicht reflektiert wird. Der andere Teil des Lichts dringt jedoch in die Ölschicht ein und wird an der Wasseroberfläche reflektiert. Konstruktive Interferenz erfolgt bei der Reflexion nur für bestimmte Wellenlängen des Lichts, wodurch die Farbenspiele bei Lichtspiegelungen an diesen Oberflächen entstehen.

Abbildung 8.2.182: Interferenz (C)
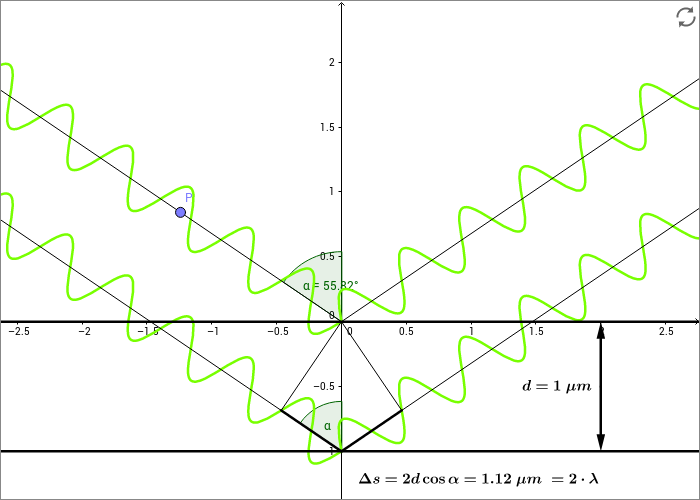
Sie können das Grundprinzip hinter diesem Phänomen mit Hilfe der folgenden animierten Skizze untersuchen. Hier ist eine Schicht der Dicke dargestellt, an deren Ober- und Unterseite jeweils ein Teil des Lichts reflektiert wird. Man erkennt, dass die an der Unterseite reflektierte Lichtwelle einen längeren Weg zurückzulegen hat als die an der Oberseite reflektierte. Nach der Reflexion überlagern sich die beiden Lichtwellen und interferieren miteinander.
In der animierten Skizze ist die zusätzliche Wegstrecke , die der untere Lichtstrahl zurückzulegen hat, eingezeichnet. Betrachtet man die Skizze, erkennt man, dass die zusätzliche Strecke sich aus den Katheten zweier rechtwinkliger Dreiecke zusammensetzt. In beiden Dreiecken bildet die Schichtdicke jeweils die Hypotenuse. Aus der Trigonometrie folgt dann, dass von der Schichtdicke und dem Einfallswinkel wie folgt abhängt:
Eine konstruktive Interferenz zwischen den beiden Teilwellen findet statt, wenn auf dieser Strecke der Phasenunterschied zwischen den beiden Wellenzügen gerade ein ganzzahliges Vielfaches von beträgt, d.h. wenn der untere Wellenzug gerade um eine oder mehrere Wellenlängen verzögert die Ölschicht verlässt ( mit einer natürlichen Zahl ). Vergrößern Sie nun den Einfallswinkel des Lichts durch Ziehen am Punkt . Hierdurch ändert sich die Strecke . Lichtwellen mit einer Wellenlänge erfahren also eine konstruktive Interferenz und werden daher reflektiert. Die Lichtwellen werden in der Skizze automatisch eingezeichnet und in etwa mit der Farbe markiert, die einer passenden Wellenlänge für die Größe entspricht. Dies bewirkt, dass unter verschiedenen Reflexionswinkeln verschiedene Spektralfarben des Lichts zurückgeworfen werden.
Die hier dargestellte Situation lässt sich direkt auf den interessanten Anwendungsfall der Bragg-Reflexion von Röntgenlicht an Kristallgittern von Festkörpern übertragen. Will man das Prinzips der Interferenz an dünnen Schichten jedoch auf den eingangs erwähnten Fall einer Ölschicht auf Wasser anwenden, so muss die obige Darstellung in zwei Punkten modifiziert werden:
- Da Öl einen anderen Brechungsindex als Luft besitzt, wird der Lichtstrahl beim Eintritt in die Ölschicht gebrochen, so dass sich die optische Länge, die das Licht in der Ölschicht zurücklegt, ändert. Eine entsprechende Berechnung ergibt . Wegen erhält man mathematisch das vorherige Resultat zurück, wenn gesetzt wird.
- Weil der Brechungsindex von Luft kleiner ist als der von Öl, ergibt sich beim Übergang von Luft zu Öl ein Phasensprung von einer halben Wellenlänge. Dies kann man beispielsweise in Analogie zur Reflexion einer Seilwelle an einer harten Wand verstehen. Weil der Brechungsindex von Öl größer ist als der von Wasser, gibt es beim Übergang von Öl zu Wasser keinen Phasensprung. Dadurch verändert sich die Bedingung für konstruktive Interferenz insgesamt zu .
Rechnerische Betrachtung der Interferenz von zwei Wellen
Rechnerische Interferenz zweier gleichläufiger Wellen gleicher Frequenz und Amplitude:
| Wellenfunktion 1 | |
| Wellenfunktion 2 (mit Gangunterschied ) | mit |
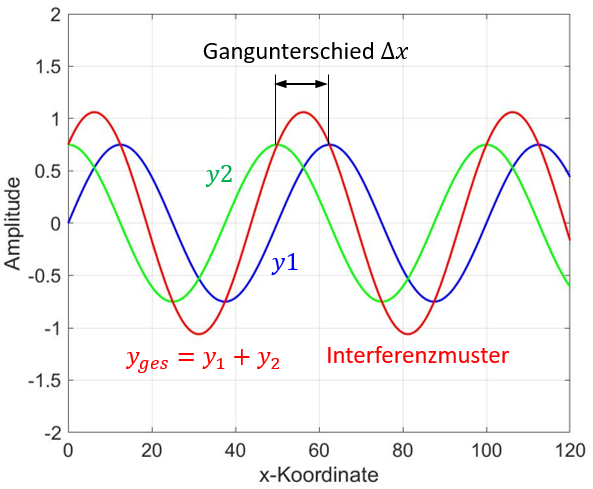
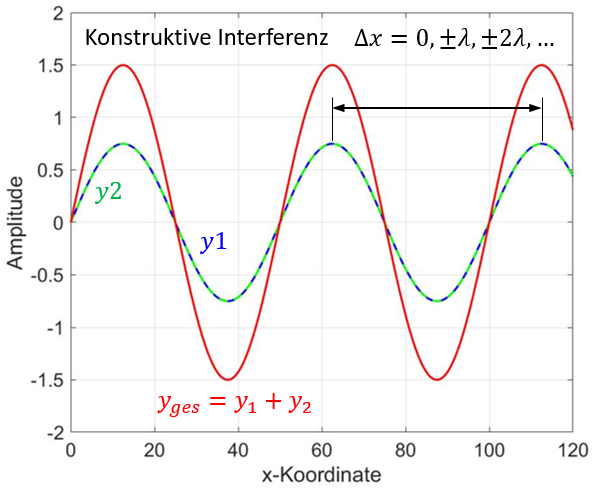
Abbildung 8.2.184: Interferenz von Wellenfunktion 1 und Wellenfunktion 2 (C)
| nach Interferenz | |
| Additionstheorem und | |
| mit folgt | |
| Max. Amplitude bei | konstruktive Interferenz |
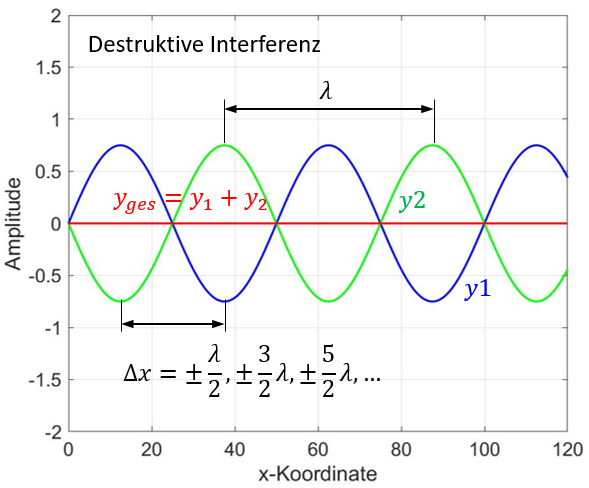
| Min. Amplitude bei | destruktive Interferenz |
| 
|
Konstruktive und destruktive Interferenz
| Gangunterschied bei konstruktiver Interferenz | mit |
| Gangunterschied bei destruktiver Interferenz |
Wenn zwei Wellen mit einem kleinen Unterschied in ihrer Frequenz bzw. Wellenlänge interferieren, entsteht eine Schwebung:
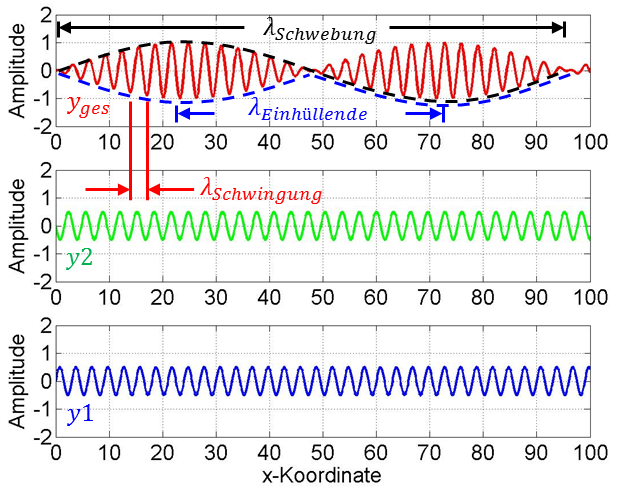
Abbildung 8.2.187: Schwebung (C)
Schwebungsbild (für ):
| Wellenzahl Schwebung: | |
| Wellenzahl Einhüllende: | |
| Wellenzahl Schwingung: |
Beugung
Wenn eine Welle auf ein Hindernis trifft und dessen Dimensionen ungefähr die gleiche Größenordnung wie die Wellenlänge haben, tritt „Beugung“ auf, d.h. die Wellen breiten sich auch in Richtungen aus, die von der geometrischen Einfallrichtung der Welle abweichen. Huygens’sches Prinzip: viele Elementarkugelwellen überlagern sich zu neuen Wellenfronten.
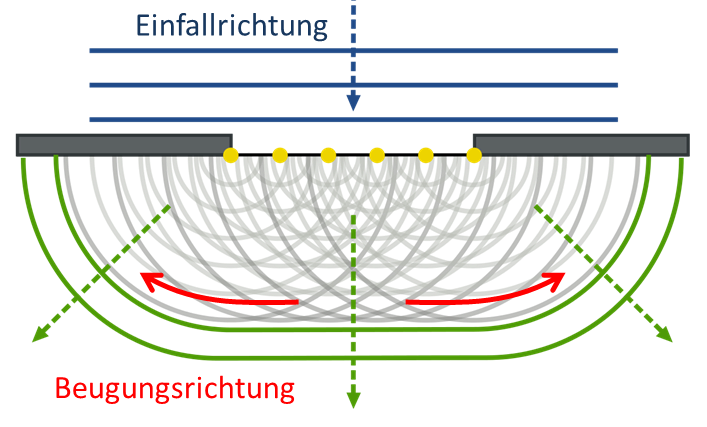
Wenn eine Welle auf ein Hindernis trifft und dessen Dimensionen ungefähr die gleiche Größenordnung wie die Wellenlänge haben, tritt „Beugung“ auf, d.h. die Wellen breiten sich auch in Richtungen aus, die von der geometrischen Einfallrichtung der Welle abweichen. Huygens’sches Prinzip: viele Elementarkugelwellen überlagern sich zu neuen Wellenfronten.

Abbildung 8.2.188: Beugung an einem Spalt (C)
- Der Beugungseffekt kann bei allen Wellentypen auftreten. Z.B. kann man tieffrequenten Schall „um die Ecke“ hören (Akustik), oder Licht, das durch einen Spalt fällt, erzeugt nicht nur ein Spaltbild, sondern ein Interferenzmuster aus vielen Spaltbildern (Optik).
- „Fraunhofer’sche Beugung“: Bildschirm zur Sichtbarmachung der Beugungsmuster ist weit vom Hindernis entfernt. „Fresnel’sche Beugung“: Bildschirm ist nahe am Hindernis.
Je nachdem, wie groß die Dimension des Hindernisses relativ zur Wellenlänge ist, tritt Beugung auf (rote Pfeile) oder nicht (geometrische Ausbreitung, schwarze Pfeile).
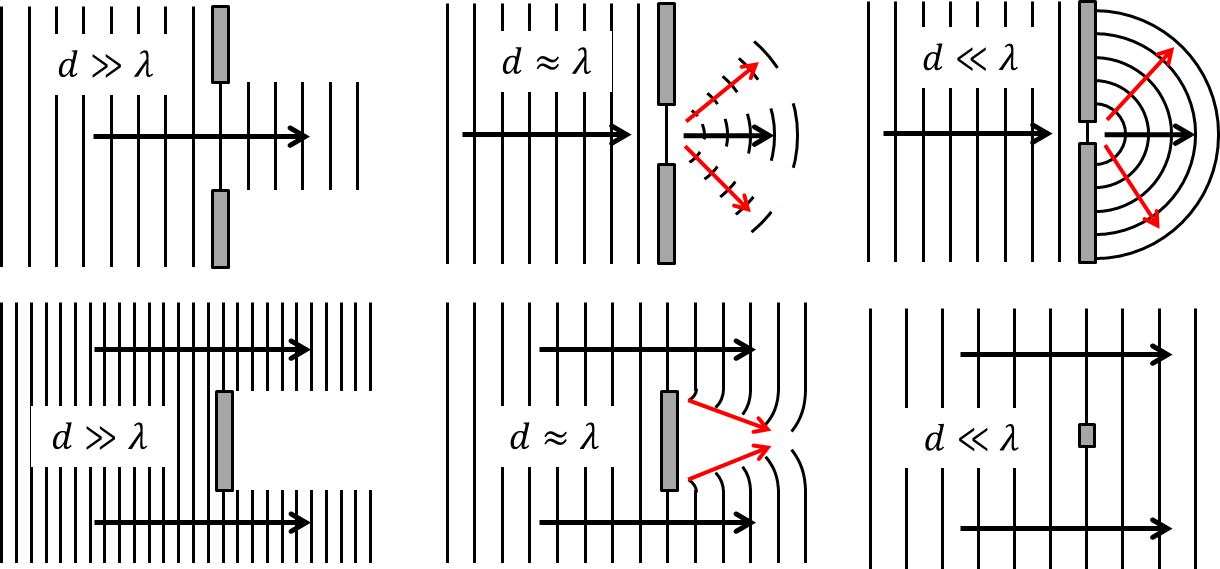
Abbildung 8.2.189: Wechselwirkung von Wellen mit verschiedenen Hindernissen (C)
Beugung am Doppelspalt
Ein Doppelspalt ist ein Hindernis, das in der Ebene senkrecht zu Ausbreitungsebene des Lichts nur an zwei Punkten die Lichtwelle passieren lässt (siehe animierte Skizze). Von diesen beiden Punkten (eigentlich sind es ja Linien) geht nun jeweils eine Elementarwelle aus. Diese beiden Elementarwellen überlagern sich und erzeugen ein Interferenzmuster.
In der folgenden animierten Skizze läuft von links eine Lichtwelle ein. Die blauen Linien sollen jeweils die Wellenberge der Welle kennzeichnen. Rechts von dem Doppelspalt ist die Ausbreitung der beiden Elementarwellen dargestellt. Dabei wurden die Schnittpunkte der Wellenberge beider Elementarwellen durch schwarze Linien miteinander verbunden. Wo zwei Wellenberge aufeinandertreffen, ergibt sich konstruktive Interferenz und damit eine große Amplitude der resultierenden Welle. Entlang der schwarzen Linien erwartet man also die Maximalamplituden des Interferenzmusters.
Sie können das Interferenzmuster beeinflussen, indem Sie den Abstand der beiden Spalte variieren oder die Wellenlänge ändern. Beobachten Sie, wie sich die Anordnung der Interferenzmaxima ändert.
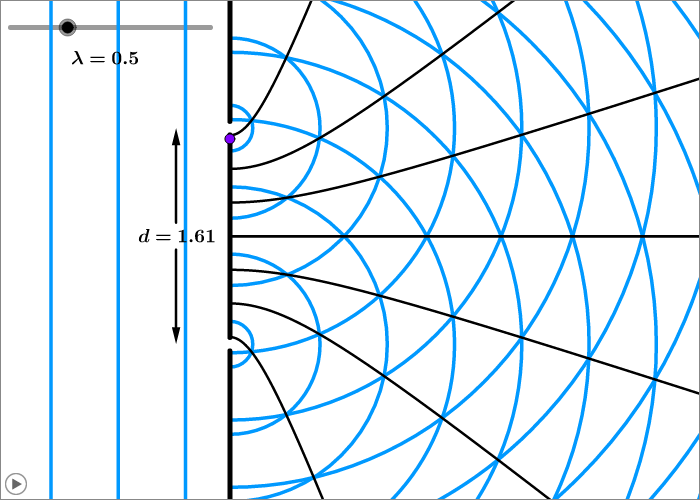
Interferenz am Doppelspalt (+)
Video 9: Interferenz am Doppelspalt (C)
.
Man kann nun wie bei der Reflexion an der dünnen Schicht auch bei der Beugung am Doppelspalt aus der Geometrie den Wegstreckenunterschied zwischen den beiden Teilwellen ermitteln, die durch die beiden Spalte erzeugt werden. Dies ist in der folgenden animierten Skizze dargestellt. Wir gehen im Folgenden davon aus, dass das Interferenzbild auf einem weit entfernten Schirm betrachtet wird. Zur Berechnung des Wegstreckenunterschieds kann man dann die von den beiden Spalten ausgehenden Strahlen näherungsweise als parallel annehmen. Der Wegstreckenunterschied ergibt sich dann aus dem Spaltabstand und dem Winkel , unter dem man den Spalt betrachtet, zu
In der animierten Skizze geht man nun davon aus, dass weißes Licht, also Licht als Gemisch verschiedener Wellenlängen, von links auf den Doppelspalt fällt. Wenn Sie nun durch Ziehen an dem Punkt den Winkel vergrößern, wird die Strecke eine Größe erreichen, die den Wellenlängen des sichtbaren Lichts entspricht. Es kommt dann gerade für die Farbe zu konstruktiver Interferenz, bei der eine Wellenlänge genau in die Wegstreckendifferenz passt. Dies ist durch eine entsprechende Farbe des Wellenzuges angedeutet. Ändern Sie die Richtungen zu größeren Beugungswinkeln , so erscheinen auch Interferenzmaxima höherer Ordnung, bei denen zwei, drei oder mehr Wellenlängen in die Strecke passen. Untersuchen Sie auch, wie die Beugungsrichtungen der verschiedenen Farben von dem Abstand der beiden Spalte abhängen.
Ein Doppelspalt ist also in der Lage, das weiße Licht in seine Spektralfarben zu zerlegen. In der Praxis wird für die spektrale Zerlegung des Lichts durch Beugung aber in der Regel kein Doppelspalt, sondern ein Gitter verwendet. In diesem Gitter befinden sich sehr viele Spalte mit regelmäßigem Abstand , die im Wesentlichen das gleiche Beugungsmuster wie der Doppelspalt erzeugen, allerdings mit wesentlich höherer Intensität und Trennschärfe.
Beispiel
8.2.9
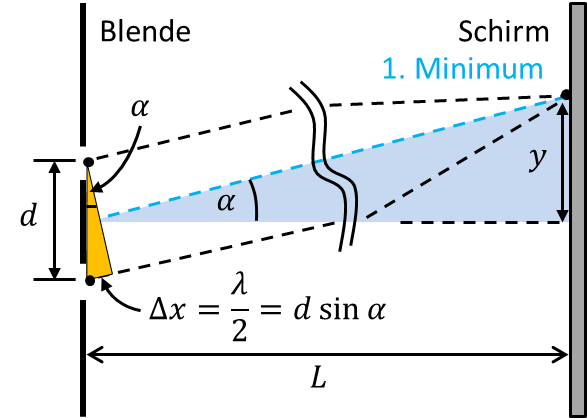
Sie machen ein Doppelspaltexperiment und bestrahlen eine Blende, in der sich zwei sehr schmale Spalte befinden, mit gelbem Licht der Wellenlänge . Die Spalte haben den Abstand . Der Schirm sei von der Blende entfernt. Auf dem Schirm erkennen Sie das dargestellte Interferenzmuster mit einem Hauptintensitätsmaximum und mehreren Nebenmaxima und -minima.
Berechnen Sie die Entfernung des 1. Intensitätsminimums auf dem Schirm von der Hauptachse.
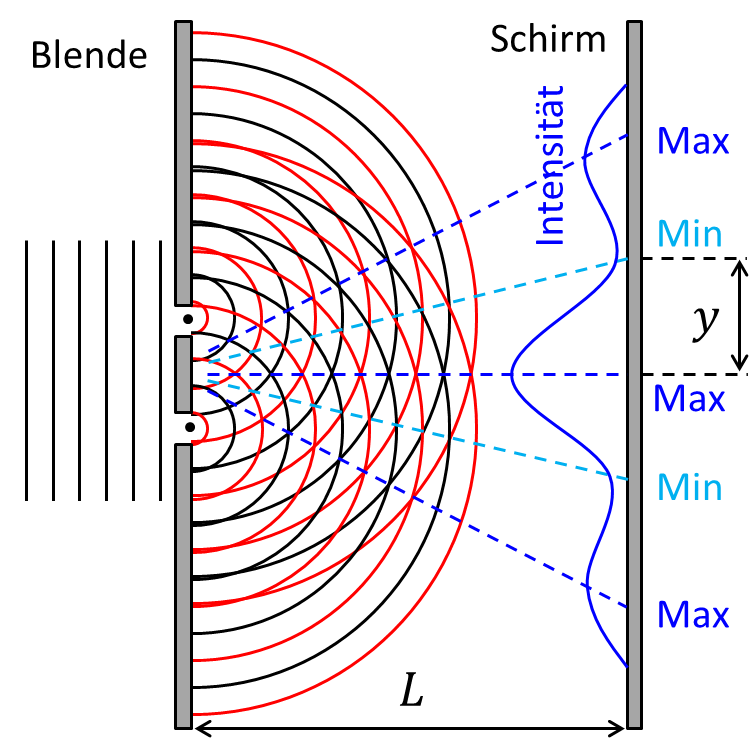
Sie machen ein Doppelspaltexperiment und bestrahlen eine Blende, in der sich zwei sehr schmale Spalte befinden, mit gelbem Licht der Wellenlänge . Die Spalte haben den Abstand . Der Schirm sei von der Blende entfernt. Auf dem Schirm erkennen Sie das dargestellte Interferenzmuster mit einem Hauptintensitätsmaximum und mehreren Nebenmaxima und -minima.
Berechnen Sie die Entfernung des 1. Intensitätsminimums auf dem Schirm von der Hauptachse.

Abbildung 8.2.191: Doppelspaltexperiment (C)