2. Mechanik
  3. Kräfte und ihre Wirkungen
  4. Druck und Auftrieb (!),(+)

4.1.6 Druck und Auftrieb





 

Basiswissen „Dichte der Stoffe“


Wenn man unterschiedliche Körper betrachtet, finden sich Körper, die das gleiche Volumen einnehmen, aber unterschiedlich schwer sind. Ein einfaches Beispiel sind zwei Würfel mit den Kantenlängen 10 cm. Ein Würfel soll aus Eisen und einer aus Holz sein. Ermittelt man das Gewicht dieser Würfel, erhält man für das Gewicht des Eisenwürfels etwa 7,8 kg und für einen Holzwürfel aus Buchenholz etwa 0,74 kg. Man kann aber auch Körper aus den beiden Materialien finden, die die gleiche Masse haben, aber unterschiedlich groß sind. Ein Eisenwürfel mit einer Kantenlänge von 4,5 cm hat eine Masse von etwa 0,74 kg. Dies ist anschaulich in der Abbildung dargestellt. Der linke und der mittlere Würfel haben das gleiche Volumen, aber unterschiedliche Masse. Der mittlere und der rechte Würfel haben zwar unterschiedliche Volumina, aber gleiche Masse.
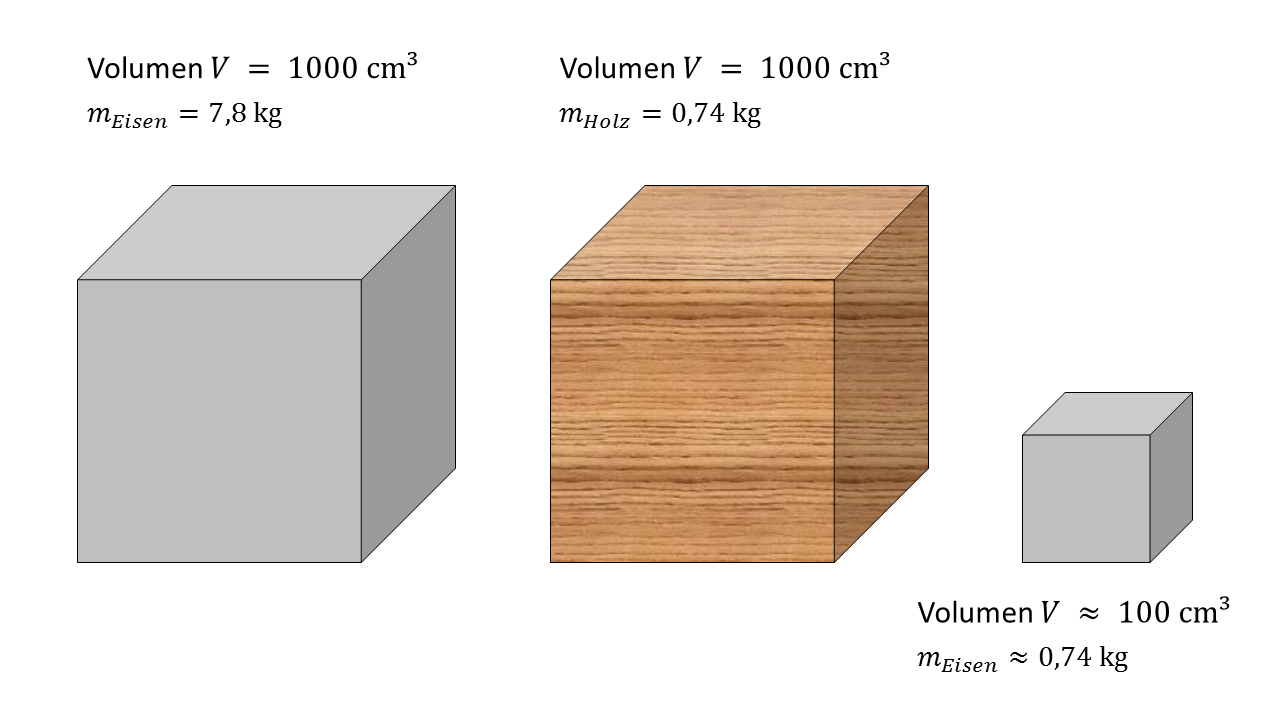
././Physikkurs/kraefte_druckauftrieb/images/DichteWuerfel.png
Abbildung 4.1.263: Dichte und Volumen von Würfeln (C)


Bei einem Körper ist das Verhältnis zwischen Masse und Volumen vom Material abhängig. Es handelt sich hier um eine Kenngröße des Materials.
Das Verhältnis zwischen der Masse m und dem Volumen V eines Körpers wird als Dichte ρ bezeichnet:

ρ= m V  .

Bei der Dichte handelt es sich um eine Materialeigenschaft. Sie ist abhängig von der Temperatur.
Die SI-Einheit der Dichte ist [ρ] SI = kg m3 .
Praktisch gebräuchliche Einheiten sind abgeleitete Einheiten wie [ρ]= g cm3 ​= kg dm3 = 103   kg m3 .
Untersucht man das Verhalten eines Körpers bei verschiedenen Temperaturen, kann man feststellen, dass das Volumen eines Körpers von seiner Temperatur abhängt. Körper dehnen sich bei zunehmender Temperatur aus. Dabei bleibt ihre Masse aber konstant. Das bedeutet, dass ihre Dichte kleiner wird. Die Dichte ist also von der Temperatur abhängig.
Beispiel 4.1.54  
Ein Gartentor mit einem Metallschloss funktioniert im Frühjahr und Herbst ohne Probleme. Im Winter bei kalten Temperaturen beobachten Sie, dass das Tor oft aufgeht. Der Riegel verändert seine Länge, er wird kürzer und das Tor schließt nicht mehr. Im Gegensatz dazu beobachten Sie im Sommer, wenn es sehr heiß ist, dass das Tor klemmt und nicht mehr zu öffnen ist. Der Riegel hat sich ausgedehnt.
Dieses Verhalten muss bei der Entwicklung und beim Bau von Maschinen und Anlagen beachtet werden, um die volle Funktionsfähigkeit und die Sicherheit zu gewährleisten. So muss ein Ingenieur schon bei der Konstruktion von Rohrleitungen berücksichtigen, das diese sich im Betrieb erwärmen können und ihre Länge ändern, insbesondere weil in komplexen Anlagen eine Vielzahl von Abzweigungen und Zugängen existieren. Im kalten Zustand werden die Systeme montiert, nach Inbetriebnahme erreichen Sie ihre Temperatur und dehnen sich aus. Auch dann muss das komplette System an Ort und Stelle sein und darf nicht kaputt gehen.

Dichten verschiedener Stoffe sind in Büchern tabelliert. Dabei wird im Allgemeinen die Temperatur, bei der die Werte ermittelt wurden, mit angegeben. In der folgenden Tabelle sind die Dichten einiger Materialien aufgeführt. Weitere Daten sind in einschlägigen Tabellenwerken oder auch in der Tabellensammlung Chemie/ Dichte fester Stoffe zu finden.

 Material   Dichte [ρ]= g cm3   Temperatur [T]= ∘ C  
 Blei    11,342   20  
 Quarzglas    2,201    
 Gold    19,302   20  
 Kupfer    8,92   20  
 Stahl, unlegiert    7,85    
Beispiel 4.1.55  
Sie haben eine Metallkugel mit der Masse m=250 g und einem Volumen V=28  cm3 . Um welches Material könnte es sich nach obiger Tabelle handeln?
Mit Hilfe der Gleichung können wir die Dichte der Kugel bestimmen:
 
ρ= m V ​ = 250 g 28  cm3 ​≈8,929  g cm3 ​≈8,9  g cm3  .
 
Es handelt sich also um eine Kugel aus Kupfer.


Wenn in den folgenden Aufgabentexten nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie g=9,81  m s2  .
Aufgabe 4.1.56  
 
In einen Tank werden 7,0  m3 Heizöl gefüllt. Welche Masse hat das Öl?
Die Dichte von Heizöl liegt bei 0,92  g   cm3 .
6440 kg
920 kg
644 kg
131429 kg
 
Aufgabe 4.1.57  
 
Zwei Körper nehmen den gleichen Rauminhalt ein. Die Masse m1 des ersten Körpers soll viermal so groß sein wie die Masse m2 des zweiten Körpers. Wie verhalten sich die Dichten ρ1 und ρ2 der Körper zueinander?
 
Das hängt von der Form des Körpers ab und darüber wurde nichts gesagt.
Die Dichten sind gleich groß.
Die Dichte ρ1 des ersten Körpers beträgt ein Viertel der Dichte ρ2 des zweiten Körpers.
Die Dichte ρ1 des ersten Körpers ist viermal so hoch wie die Dichte ρ2 des zweiten Körpers.
 
Aufgabe 4.1.58  
 
Welche Kantenlänge a hat ein Würfel aus purem Gold mit der Masse m=1 kg?
Die Dichte von Gold beträgt ρ=19,3  g   cm3  .
a  = 

 


 

Definition des Drucks (!)


Video 22: Definition des Drucks (C) .



Eine Kraft, die von außen auf ein flüssiges oder gasförmiges Medium wirkt, wird im Inneren gleichmäßig in alle Richtungen weitergegeben. Um dies zu quantifizieren, wird als physikalische Größe der Druck p eingeführt. Man geht von einer äußeren Kraft F aus, die senkrecht auf eine ebene äußere Fläche A des Mediums wirkt, z.B. ein Kolben, der ein Gasvolumen abschließt. Der Druck ist dann der Quotient aus der Kraft F und der Fläche A:

p= F A  .



Genauer gesagt handelt es sich hier um den statischen Druck. Dieser statische Druck, der durch die Wirkung einer äußeren Kraft auf eine äußere Fläche des Mediums erzeugt wird, ist an dieser Fläche, an allen anderen äußeren Flächen sowie auch an jedem Ort innerhalb des Mediums gleich groß.

Die SI-Einheit des Drucks ist das Pascal:

1 Pa=1  N m2  .



Weiterhin wird häufig noch das bar benutzt. Dieses ist keine SI-Einheit, kann aber leicht von und zu Pascal umgerechnet werden:

1 bar= 105  Pa .

Ein Druck von 1  bar entspricht ungefähr dem Atmosphärendruck.

Video 23: Beispiel Konservenglas (C) .



Beispiel 4.1.59  
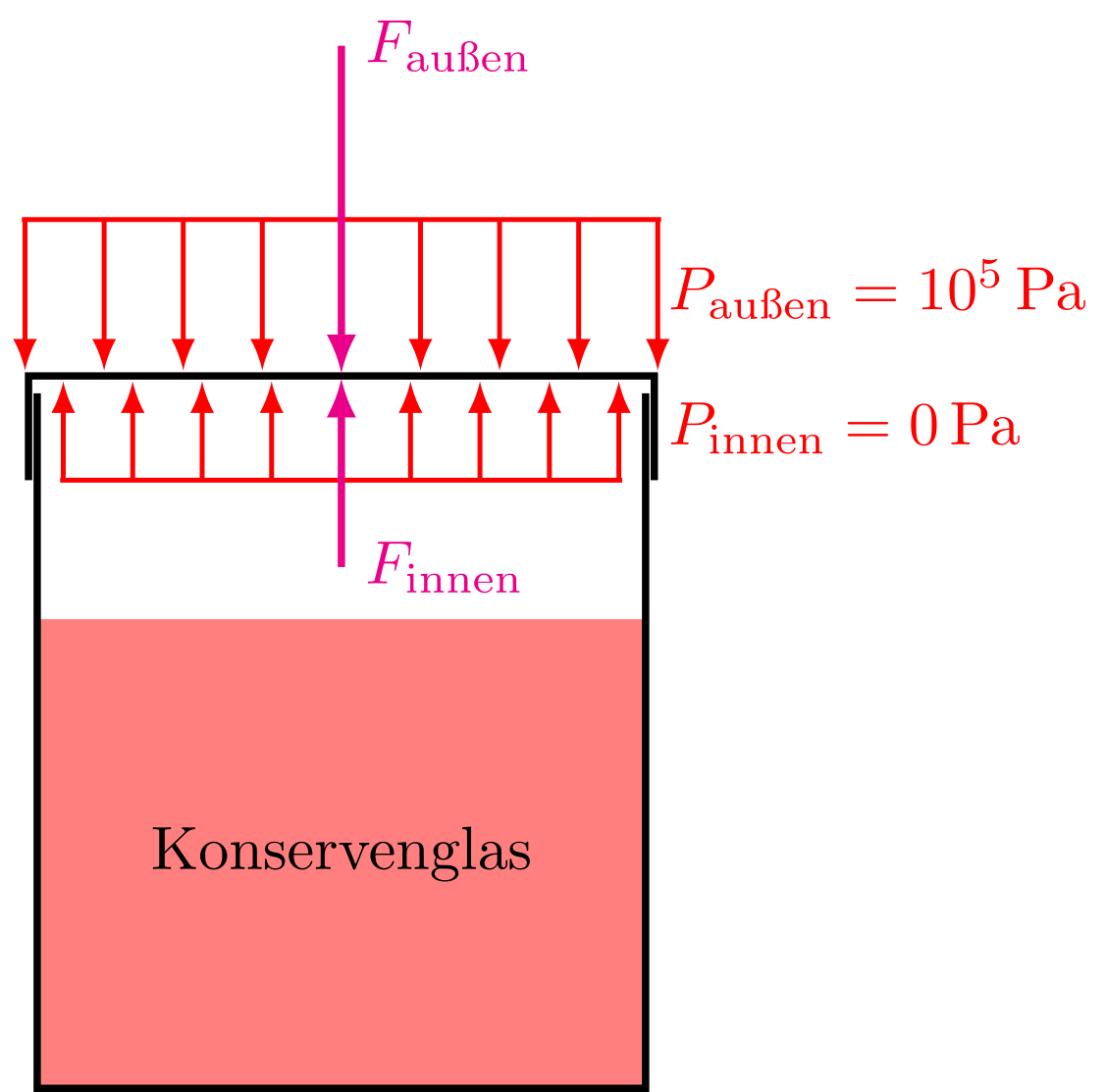
./_C85FC8CC_4x.png
Abbildung 4.1.264: Konservenglas mit Vakuumverschluss  (C)

Welche Kraft wirkt auf den Deckel eines Vakuumverschlusses eines Konservenglases, der einen Durchmesser von 5 cm hat?

Der Druckunterschied zwischen den beiden Seiten des Deckels ist gerade der Atmosphärendruck, also ca. 105  Pa,
 
F=p A ​ = 105  Pa π (0,025 m )2 ​≈196 N .
 


Video 24: Schweredruck in Flüssigkeiten (C) .



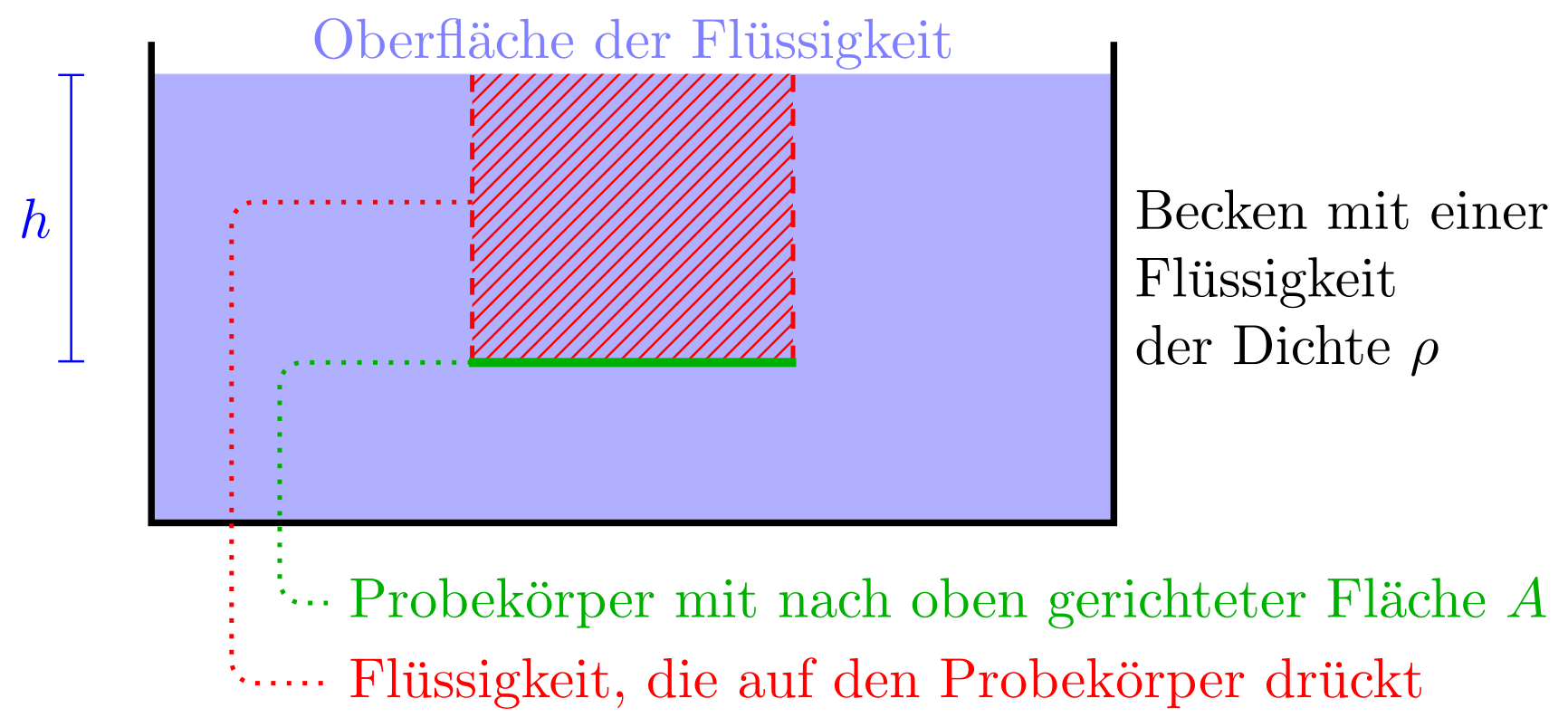
./_6F0618BC_4x.png
Abbildung 4.1.265: Schweredruck in Flüssigkeiten  (C)

Bisher entstand der Druck durch die Einwirkung einer äußeren Kraft. In Medien, bei denen die oberen Schichten durch ihre Gewichtskraft auf die unteren Schichten drücken, entsteht Schweredruck. In Flüssigkeiten wird dieser auch als hydrostatischer Druck bezeichnet. Betrachten wir nun eine dünne Flüssigkeitsschicht der Fläche A in der Tiefe h. Auf sie wirkt die Gewichtskraft der über ihr liegenden Flüssigkeitssäule. Bei einer Flüssigkeit der Dichte ρ ergibt sich für diese Kraft:
 
F=g m ​ =g ρ V ​ =g ρ h A .
 
Mit der obigen Beziehung für den Druck erhält man dann als Schweredruck

p= F A =g ρ h .

D.h. der Schweredruck ist proportional zur Höhe der Flüssigkeitssäule bzw. zur Tiefe unterhalb der Flüssigkeitsoberfläche. Bei Gasen ist die Situation unterschiedlich, da die kompressibel sind und sich daher ihre Dichte mit der Höhe ändert.


Video 25: Beispiel Wasserdruck (C) .



Beispiel 4.1.60  
Wie groß ist der Wasserdruck in 100 m Tiefe?
 
p=g ρ h ​ =9,81  m s2 ​ · 1000  kg m3 ​ · 100 m ​≈ 106  Pa ​ =10 bar .
 
Hieraus lässt sich die Faustformel ableiten, dass pro 10 m Wassertiefe der Druck um 1 bar ansteigt.


Video 26: Schweredruck in Flüssigkeiten, Ergänzung des Luftdrucks (C) .



In den meisten Fällen herrscht über der Oberfläche der Flüssigkeit kein Vakuum. Dann gibt es noch einen Luftdruck p0 , der auf die gesamte Flüssigkeitsoberfläche wirkt.
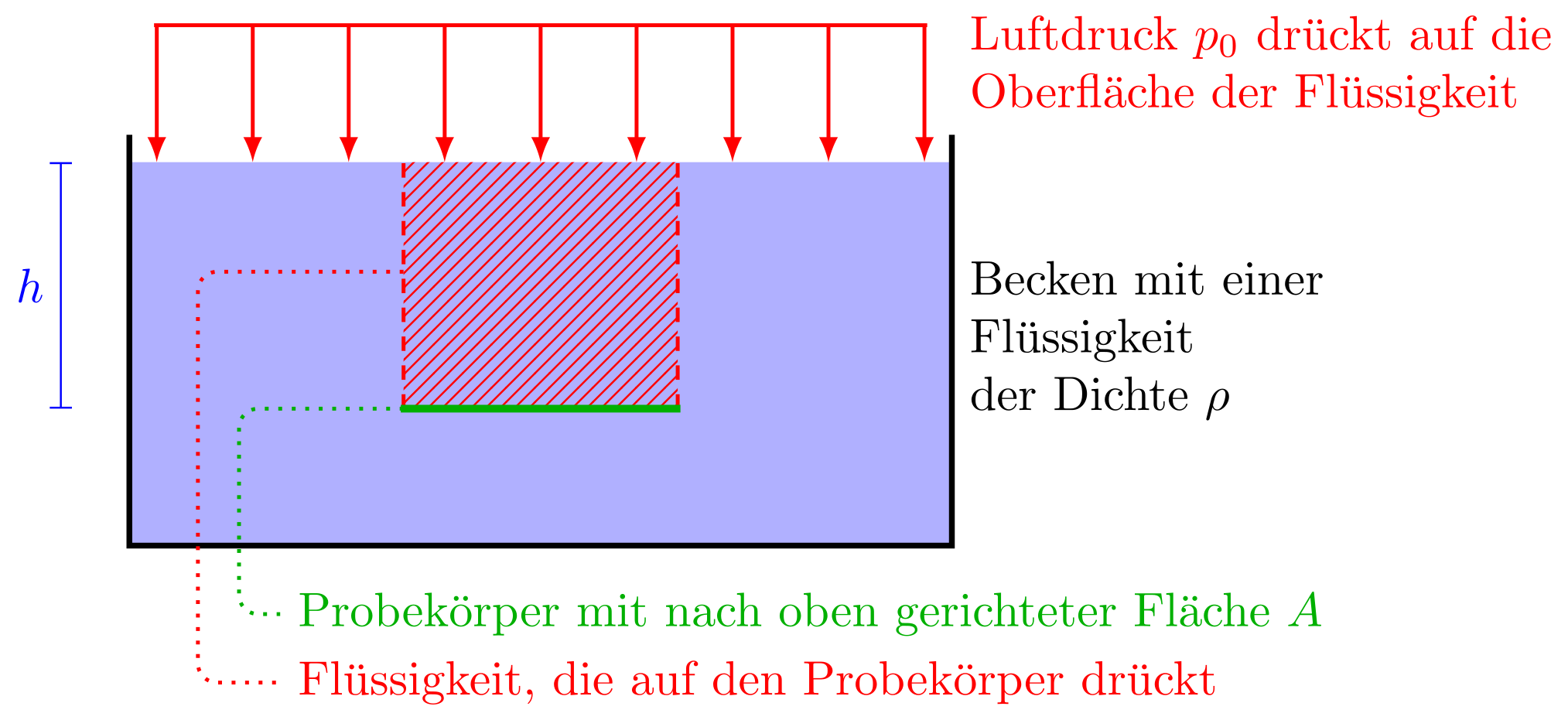
./_6A6913A9_4x.png
Abbildung 4.1.266: Schweredruck in Flüssigkeiten, Ergänzung des Luftdrucks  (C)

Der Luftdruck drückt auf die Oberfläche der Flüssigkeit und die Flüssigkeit drückt auf die Oberfläche des Probekörpers. Der Gesamtdruck, der auf die Oberfläche des Probekörpers drückt, ist damit
 
p(h)= p0 + F A ​ = p0 +g ρ h .
 
Die folgende Abbildung zeigt, wie der Druck mit zunehmender Tiefe unterhalb der Flüssigkeitsoberfläche steigt.
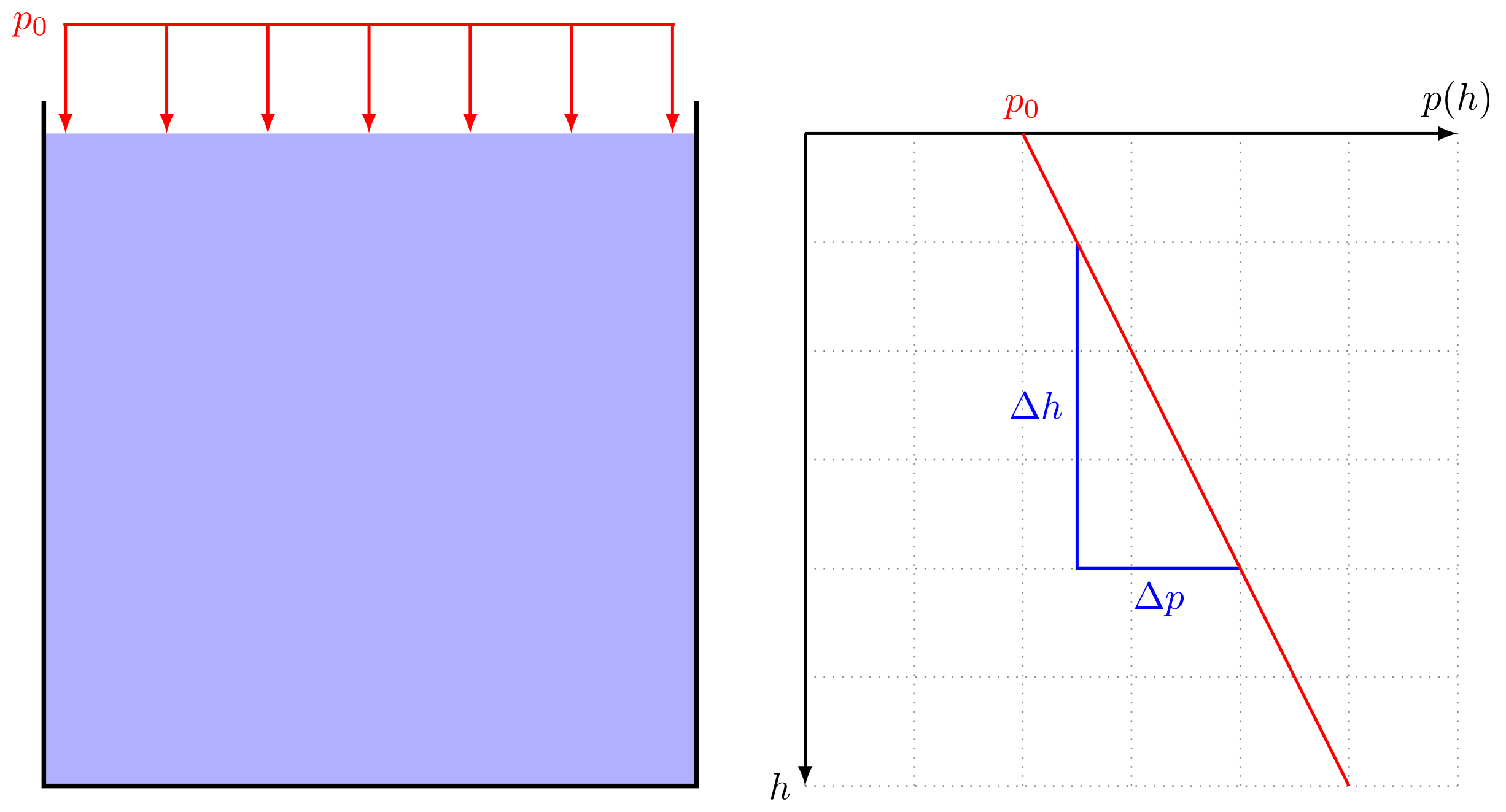
./_016EAC60_4x.png
Abbildung 4.1.267: Hydrostatischer Druck in zunehmender Tiefe  (C)



 

Auftrieb (+)


Video 27: Auftrieb (C) .



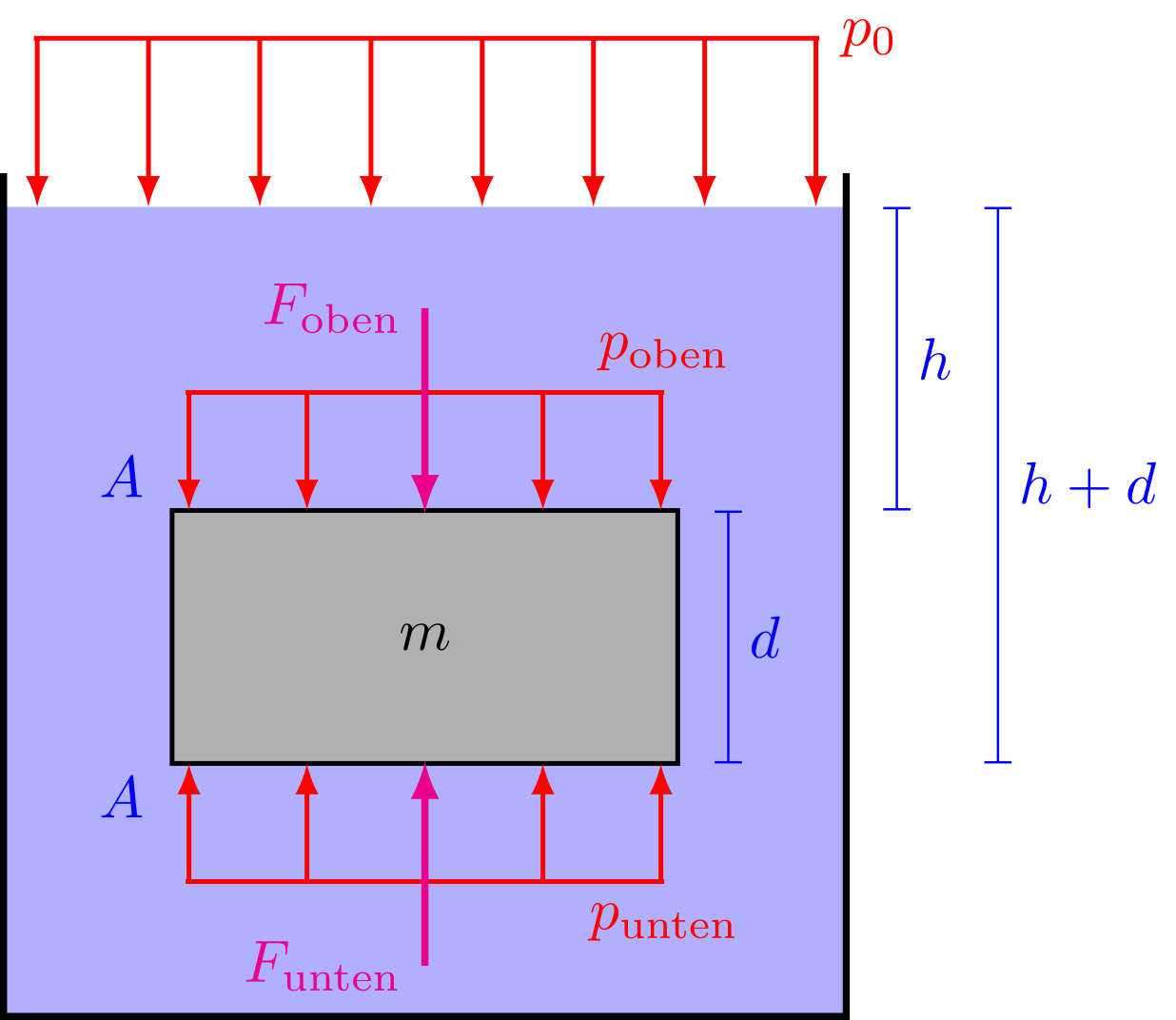
./_00A44B10_4x.png
Abbildung 4.1.268: Druckkräfte auf einen untergetauchten Körper  (C)

Ist ein Körper vollständig in einer Flüssigkeit untergetaucht, so wirkt auf ihn an der Unterseite ein höherer hydrostatischer Druck als an der Oberseite. Denn dieser nimmt ja mit der Tiefe unter der Flüssigkeitsoberfläche zu. Die Differenz zwischen diesen beiden Kräften bezeichnet man als Auftriebskraft F A . Anhand der Skizze sieht man leicht, dass sich für einen quaderförmigen Körper Folgendes ergibt:
 
F A ​ =g ρ A (h+d)-g ρ A h ​ =g ρ A d=g ρ V .
 
Dieses Ergebnis kann man auch für beliebig geformte Körper benutzen. Denn man kann sich vorstellen, dass diese aus vielen kleinen Quadern aufgebaut sind.


Dieses Ergebnis wird als Prinzip von Archimedes bezeichnet: „Der statische Auftrieb eines Körpers in einem Medium ist genauso groß wie die Gewichtskraft des vom Körper verdrängten Mediums.“ (Wikipedia)

Die Differenz zwischen Gewichtskraft und Auftriebskraft ergibt die Gesamtkraft, die auf den Körper wirkt und damit auch, ob dieser in der Flüssigkeit absinkt oder aufsteigt. Die Auftriebskraft hängt nach obigem Ergebnis nicht von der Dichte des Körpers ab. Daher wirken unter Wasser auf einen Stein und ein Holzstück von gleichem Volumen die gleiche Auftriebskraft. Beim Stein ist die Gewichtskraft aber größer als die Auftriebskraft, also sinkt er. Beim Holzstück ist die Gewichtskraft kleiner und daher steigt es nach oben.



 

Schwimmen von Körpern (+)


Video 28: Schwimmen (C) .



Video 29: Schwimmen: Verdrängte Flüssigkeit (C) .



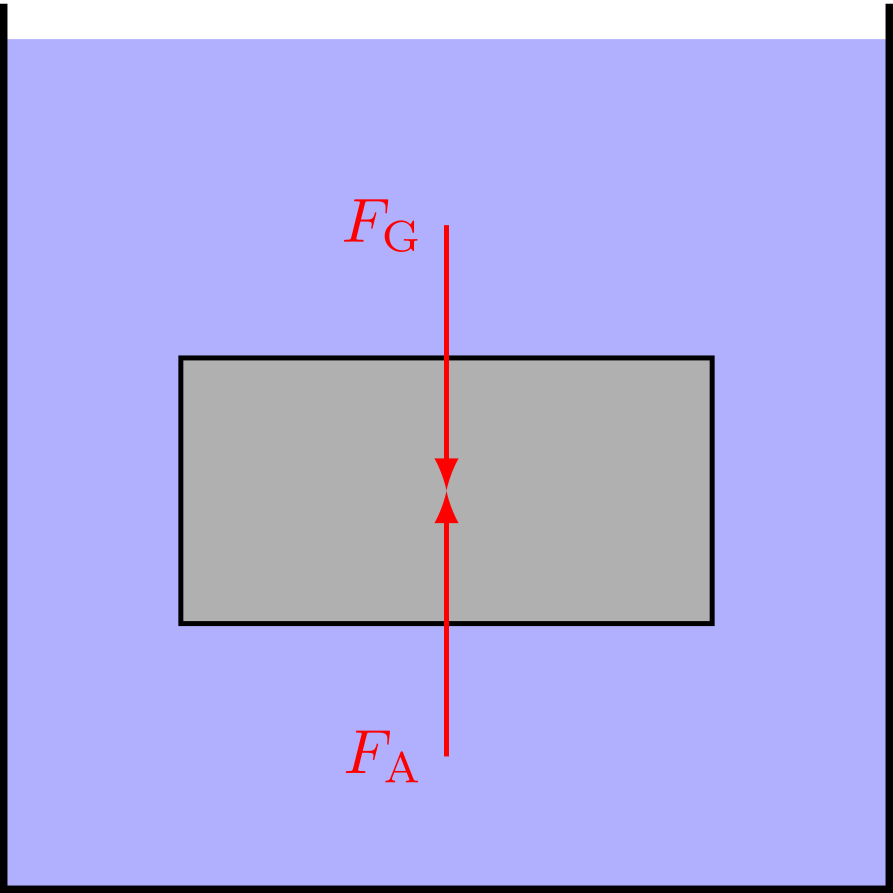
./_63383712_4x.png
Abbildung 4.1.269: Gewichtskraft und Auftriebskraft bei untergetauchtem Körper  (C)

Ein Körper steigt nach oben, wenn seine Gewichtskraft F G kleiner ist als die Auftriebskraft F A :
 
F G =g  ρ K  V ​<g  ρ F  V= F A   ⟹   ρ K < ρ F  .
 
Dies ist offenbar dann der Fall, wenn die Dichte des Körpers ρ K kleiner ist die Dichte der Flüssigkeit ρ F . Er steigt so lange nach oben, bis er aus der Flüssigkeitsoberfläche auftaucht und beginnt dort zu schwimmen.

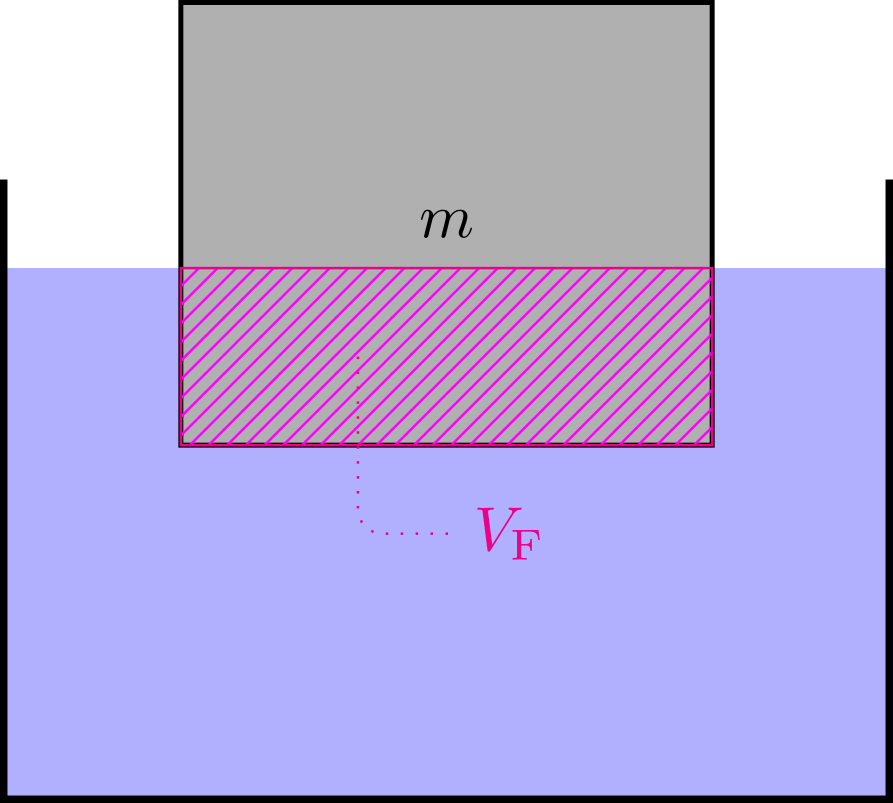
./_20BE3BD5_4x.png
Abbildung 4.1.270: Schwimmender Körper  (C)

Beim Schwimmen gilt wieder das Archimedische Prinzip. Der Körper taucht so tief in die Flüssigkeit ein, dass die Auftriebskraft, die durch das verdrängte Flüssigkeitsvolumen erzeugt wird, gerade so groß ist wie die Gewichtskraft des Körpers:
 
g  ρ K   V K =g  ρ F   V F   ⟹   ​ V F V K = ρ K ρ F  .
 




Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie g=9,81  m s2  .