4.1.5 Federkraft und hookesches Gesetz
Basiswissen „Kraft, Kraftmessung und hookesches Gesetz“
Kräfte kennt jeder aus dem Alltag. Um einen Ball zu werfen, muss man eine Kraft aufwenden. Um eine Zitrone auszuquetschen, muss man ebenfalls eine Kraft aufwenden. Schon diese beiden alltäglichen Beispiele zeigen, woran eine Kraft zu erkennen ist.
Eine Kraft verursacht die Änderung des Bewegungszustandes eines Körpers und / oder die Verformung eines Körpers.
Im Gegensatz dazu nennt man eine Verformung elastisch, wenn der Körper wieder seine ursprünglich Form annimmt, sobald keine Kraft mehr wirkt. Ein solches Verhalten findet man zum Beispiel bei Federn oder Therabändern. In einem Bereich, dem sogenannten elastischen Bereich, können Federn unter Einwirkung einer Kraft gedehnt werden und nehmen nach Ende der Krafteinwirkung ihre ursprüngliche Form und Länge wieder an. Wenn dabei die Dehnungslänge proportional zur angreifenden Kraft ist, kann dieser Effekt durch das hookesche Gesetz beschrieben werden.
Zur Ergänzung sollen noch spröde Stoffe erwähnt werden, die schon bei einer geringen plastischen Verformung zerreißen oder brechen. Ein Beispiel hierfür sind Kunststoffe die verspröden, wenn die enthaltenen Weichmacher entweichen.
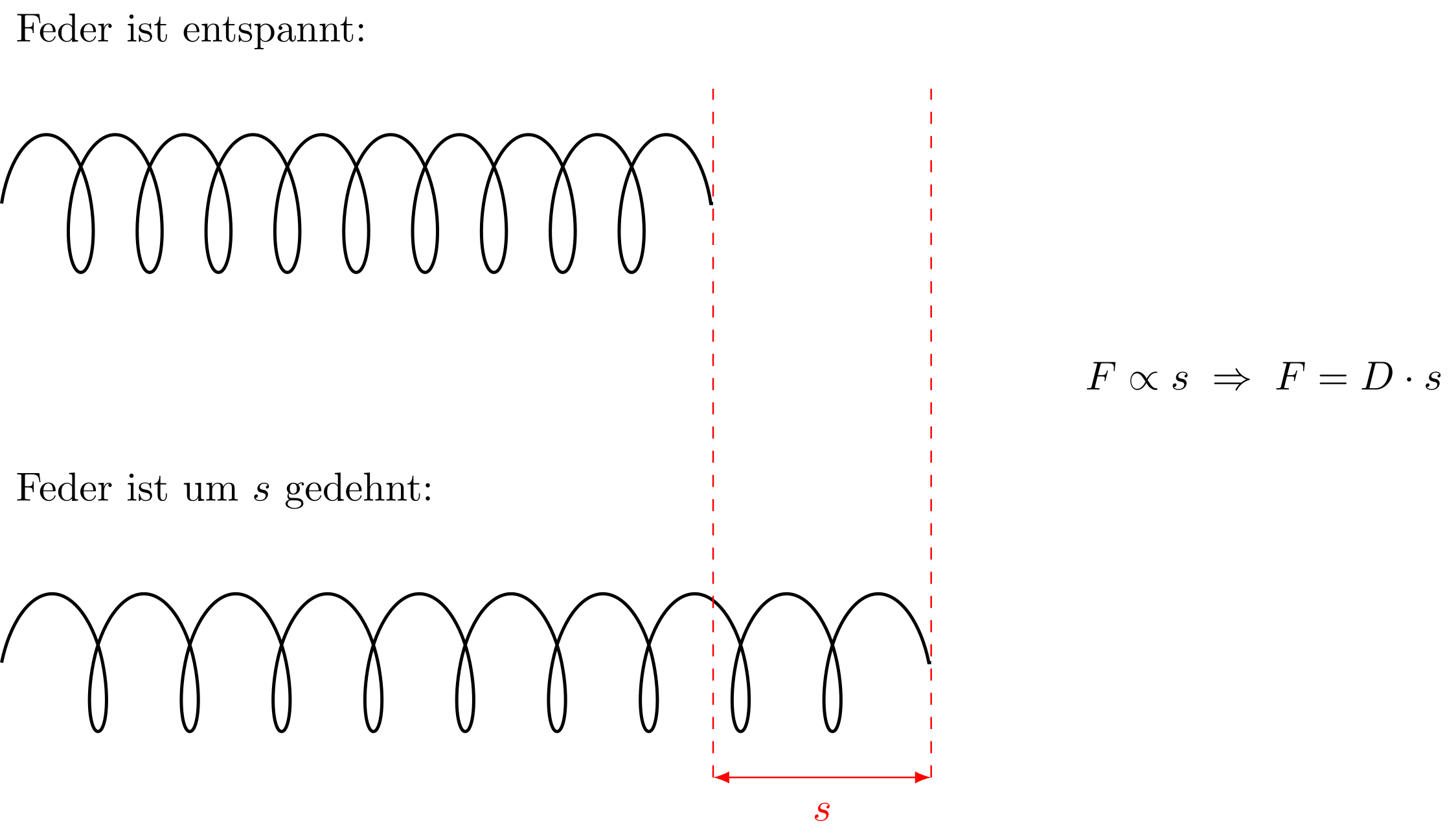
Abbildung 4.1.203: Hookesches Gesetz (C)
Die Tatsache, dass die Auslenkung einer Feder proportional zur einwirkenden Kraft ist, wird in Federwaagen genutzt. Zur Kalibrierung wird eine Feder mit verschiedenen Gewichten belastet. Es wirkt die Gewichtskraft. Auf die doppelte Masse wirkt die doppelte Gewichtskraft und führt damit zur doppelten Auslenkung. Durch das Anbringen einer Skala können Kräfte gemessen werden, wie in der Abbildung unten gezeigt ist. Für verschiedene Größenbereiche müssen verschiedene Kraftmesser verwendet werden.
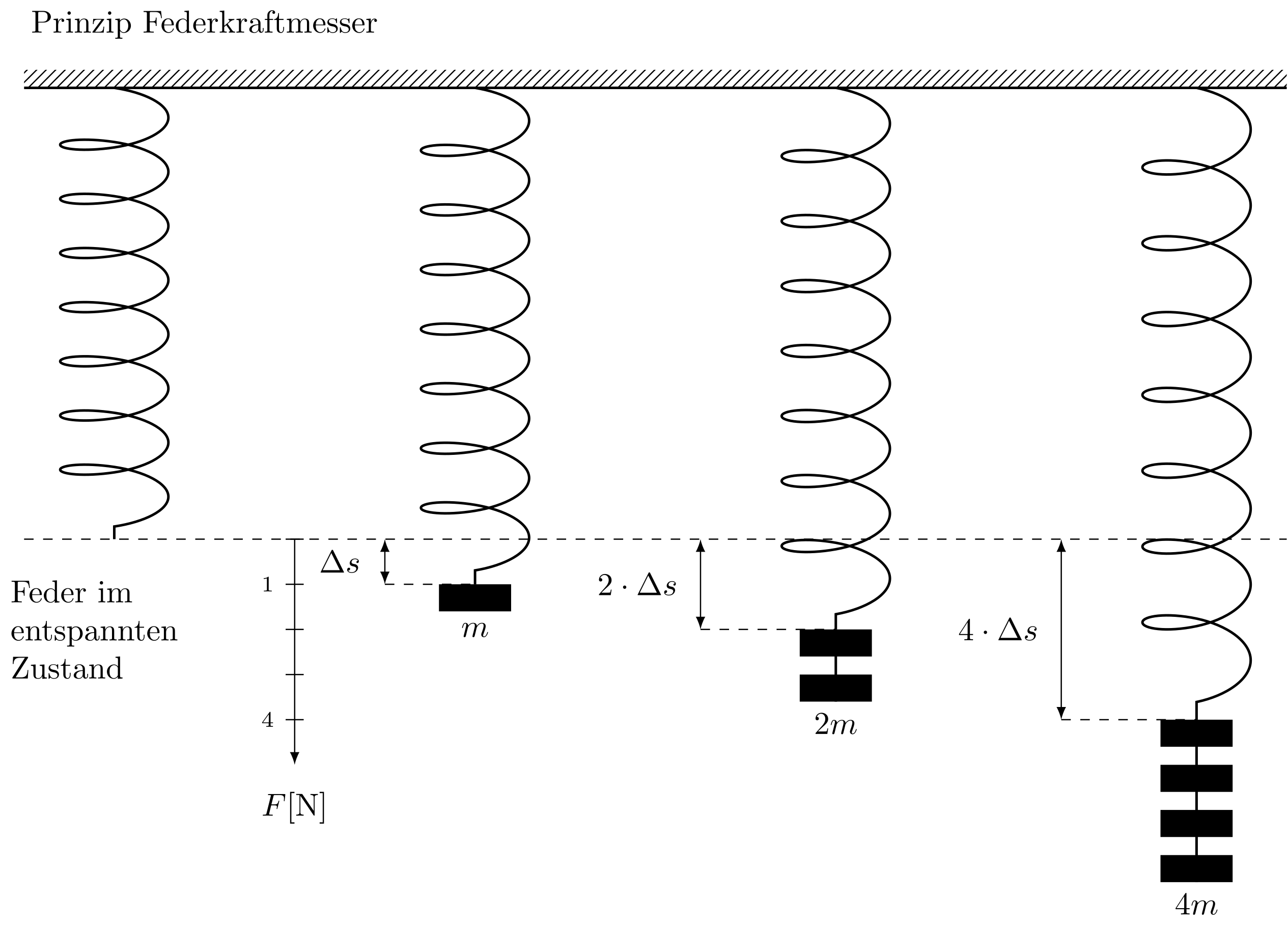
Abbildung 4.1.204: Gleiche Feder wird mit verschiedenen Gewichten belastet (C)
Beispiel
4.1.43
Die Feder einer Federwaage wird durch ein Gewicht von um verlängert. Um welchen Wert wird die Feder länger, wenn die angehängte Masse beträgt?
Wenn die dreifache Masse angehängt wird, ist nach dem Hooke'schen Gesetz auch die Auslenkung dreimal so groß. Die Verlängerung der Feder beträgt also .
Die Feder einer Federwaage wird durch ein Gewicht von um verlängert. Um welchen Wert wird die Feder länger, wenn die angehängte Masse beträgt?
Wenn die dreifache Masse angehängt wird, ist nach dem Hooke'schen Gesetz auch die Auslenkung dreimal so groß. Die Verlängerung der Feder beträgt also .
Beispiel
4.1.44
An eine Kraftwaage wird eine Masse von gehängt. Die Verlängerung der Feder beträgt . Welche Federkonstante besitzt die verbaute Feder?
Zur Lösung der Aufgabe berücksichtigen wir das das hookesche Gesetz:
Gleichzeitig wird die angehängte Masse durch die Erdanziehung in Richtung Erde beschleunigt:
Im Gleichgewichtszustand gilt dann, dass beide Kräfte gleich sein müssen, da der Körper sich nicht mehr bewegt. Durch Gleichsetzen erhält man eine Beziehung, in der die gesuchte Größe enthalten ist:
Zur Vereinfachung nehmen wir für die Fallbeschleunigung an und schreiben die Längenänderung in die SI-Einheit um. Mit ergibt sich:
An eine Kraftwaage wird eine Masse von gehängt. Die Verlängerung der Feder beträgt . Welche Federkonstante besitzt die verbaute Feder?
Zur Lösung der Aufgabe berücksichtigen wir das das hookesche Gesetz:
Gleichzeitig wird die angehängte Masse durch die Erdanziehung in Richtung Erde beschleunigt:
Im Gleichgewichtszustand gilt dann, dass beide Kräfte gleich sein müssen, da der Körper sich nicht mehr bewegt. Durch Gleichsetzen erhält man eine Beziehung, in der die gesuchte Größe enthalten ist:
Zur Vereinfachung nehmen wir für die Fallbeschleunigung an und schreiben die Längenänderung in die SI-Einheit um. Mit ergibt sich:
Wenn in den folgenden Aufgabentexten nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie
Aufgabe 4.1.46
Wieviel Newton zeigt die Federwaage rechts in der Abbildung an?
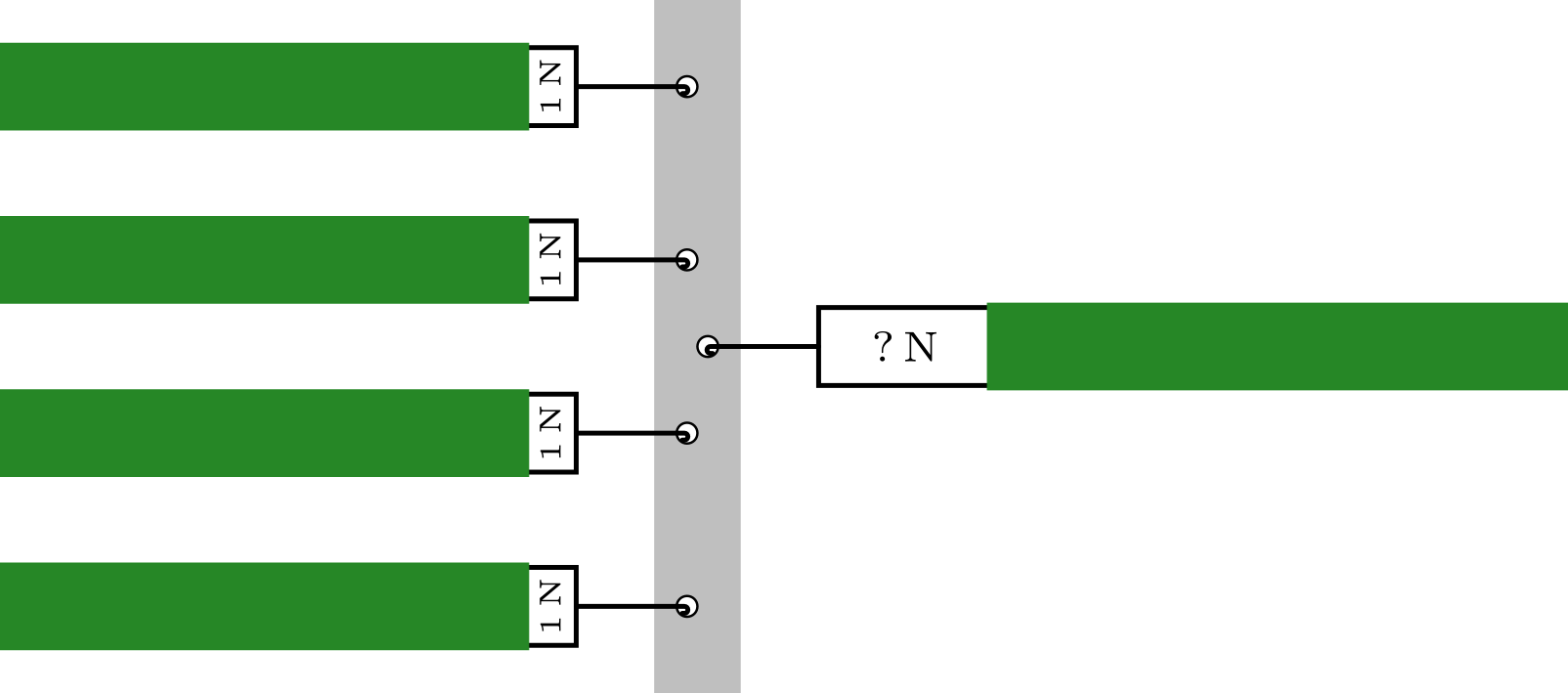
Wieviel Newton zeigt die Federwaage rechts in der Abbildung an?

Abbildung 4.1.205: Skizze zur Aufgabe (C)
| Ohne weitere Angaben ist hier keine Aussage möglich. | |
Aufgabe 4.1.47
Welche der folgenden Stoffe zeigen plastisches Verhalten?
Welche der folgenden Stoffe zeigen plastisches Verhalten?
| Glühender Stahl beim Schmieden | |
| Kaugummi | |
| Butterkekse | |
| Gummiband |
Aufgabe 4.1.48
Zwei Federn werden mit derselben Masse belastet. Die erste Feder mit der Federkonstanten verlängert sich um den fünffachen Wert der zweiten Feder mit der Federkonstanten . Wie verhalten sich die Federkonstanten zueinander?
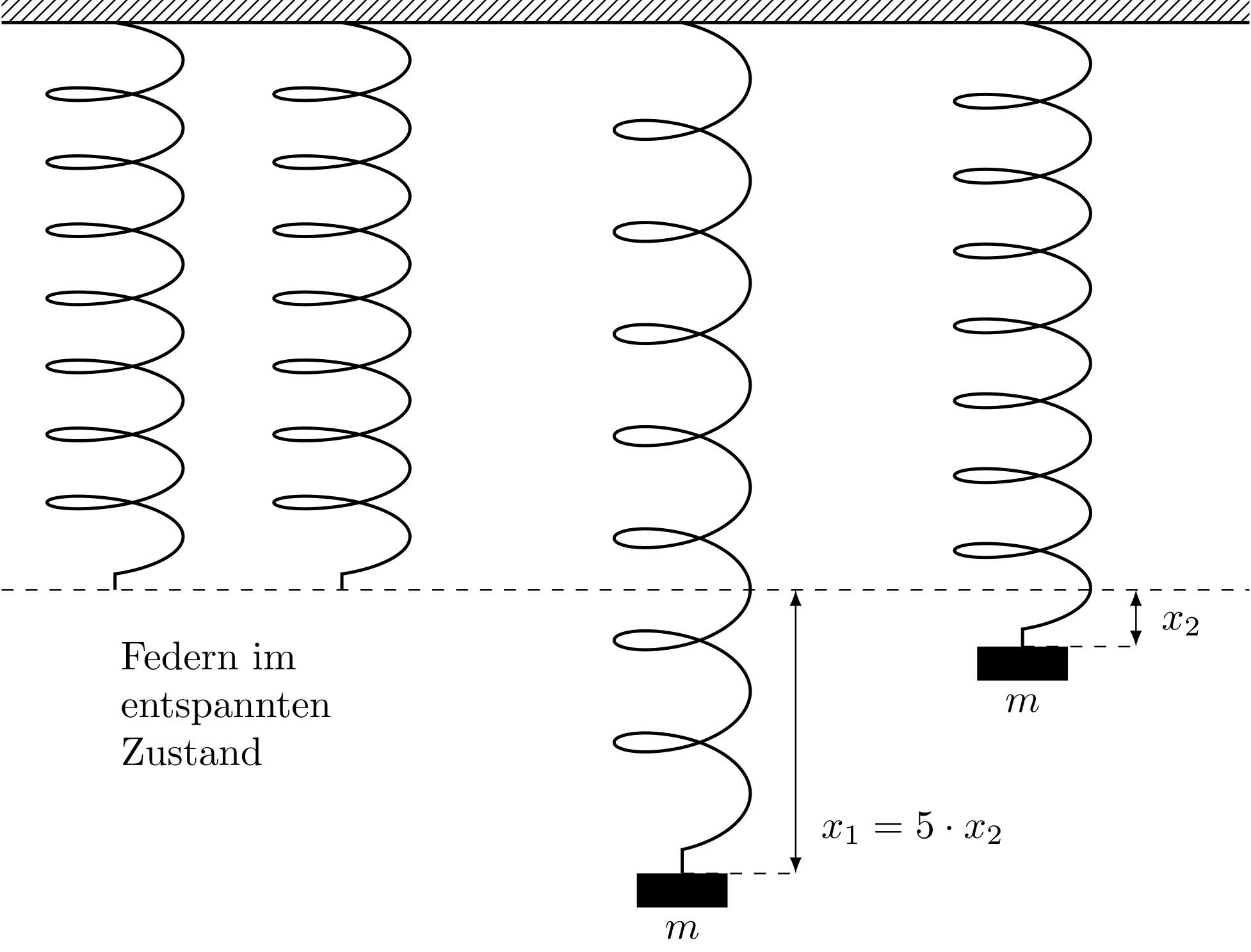
Zwei Federn werden mit derselben Masse belastet. Die erste Feder mit der Federkonstanten verlängert sich um den fünffachen Wert der zweiten Feder mit der Federkonstanten . Wie verhalten sich die Federkonstanten zueinander?

Abbildung 4.1.206: Versuchsanordnung im entspannten und belasteten Zustand (C)
Elastizität und hookesches Gesetz (!)
Video 19: Elastizität und hookesches Gesetz (C)
.

Abbildung 4.1.207: Metallstab unter Zug (C)

Abbildung 4.1.208: Metallstab unter Druck (C)
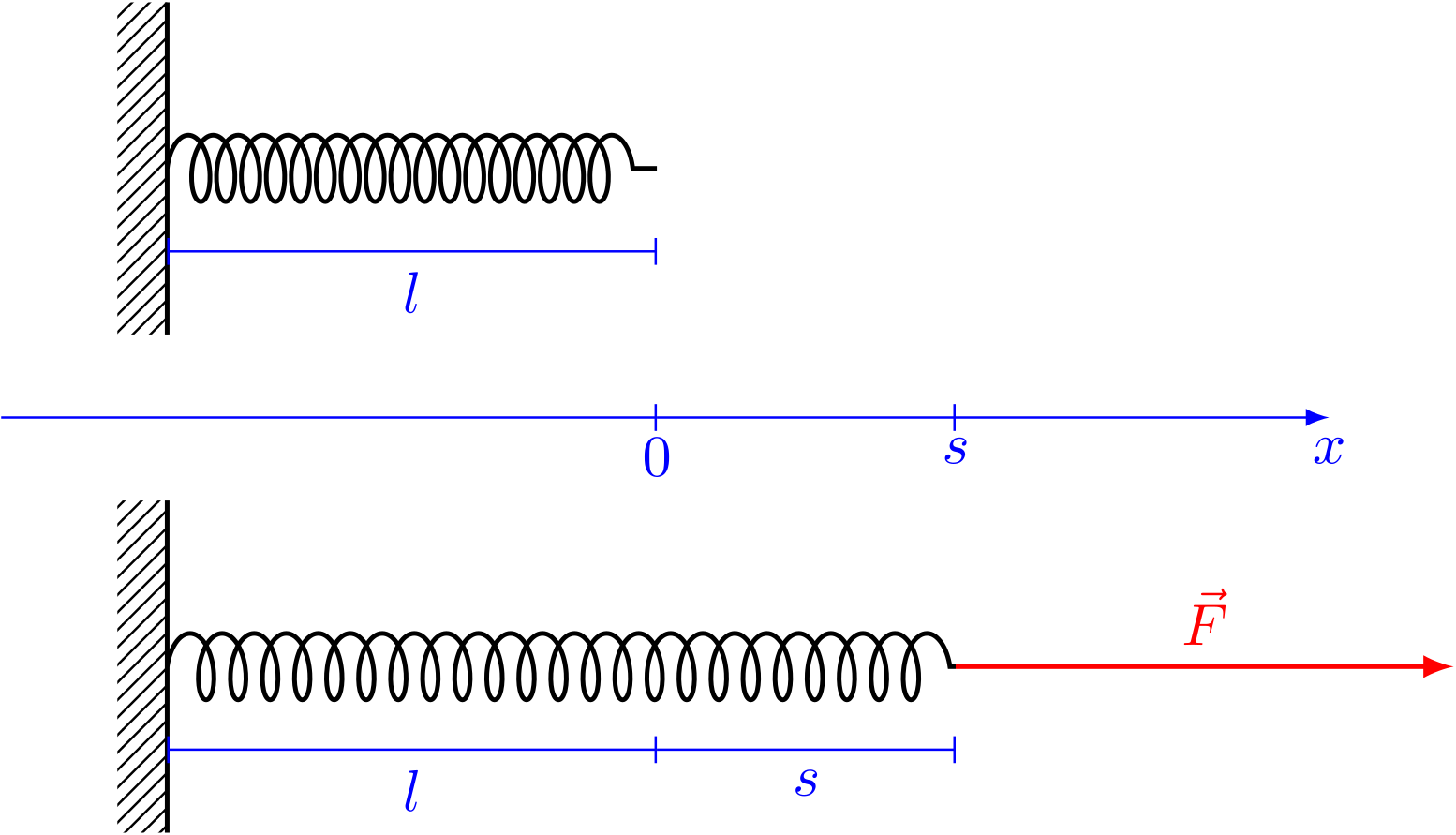
Abbildung 4.1.209: Feder unter Einwirkung von Kraft (C)
Man nennt die Federkonstante, weil sie eine für eine Spannfeder charakteristische Größe ist.

Abbildung 4.1.210: Zugkraft einer Feder (C)
Beispiel
4.1.49
Eine Feder dehnt sich bei einer Zugkraft von um aus. Welche Zugkraft wird für eine Dehnung von benötigt?
Eine Feder dehnt sich bei einer Zugkraft von um aus. Welche Zugkraft wird für eine Dehnung von benötigt?
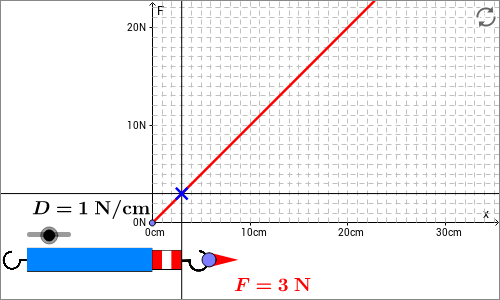
Skizze: In der folgenden interaktiven Skizze wird die Funktionsweise einer Federwaage illustriert, wie Sie sie wahrscheinlich aus dem Physikunterricht kennen. Verschieben Sie den Punkt am Federhaken und variieren Sie dadurch die Auslenkung der Federwaage. Die hierfür nötige Kraft wird durch den Kraftvektor angezeigt. Je größer die ziehende Kraft, um so größer ist die Auslenkung der Federwaage. Zusätzlich ist die Kraft gegen die Auslenkung als Graph aufgetragen. Man erkennt den proportionalen Zusammenhang. Die Steigung des Graphen ist gerade die Federkonstante . Variieren Sie auch die Federkonstante der Federwaage mit Hilfe des Schiebereglers und ändern Sie damit die Steigung des Graphen.
Parallelschaltung von Federn (*)
Video 20: Parallelschaltung von Federn (C)
.
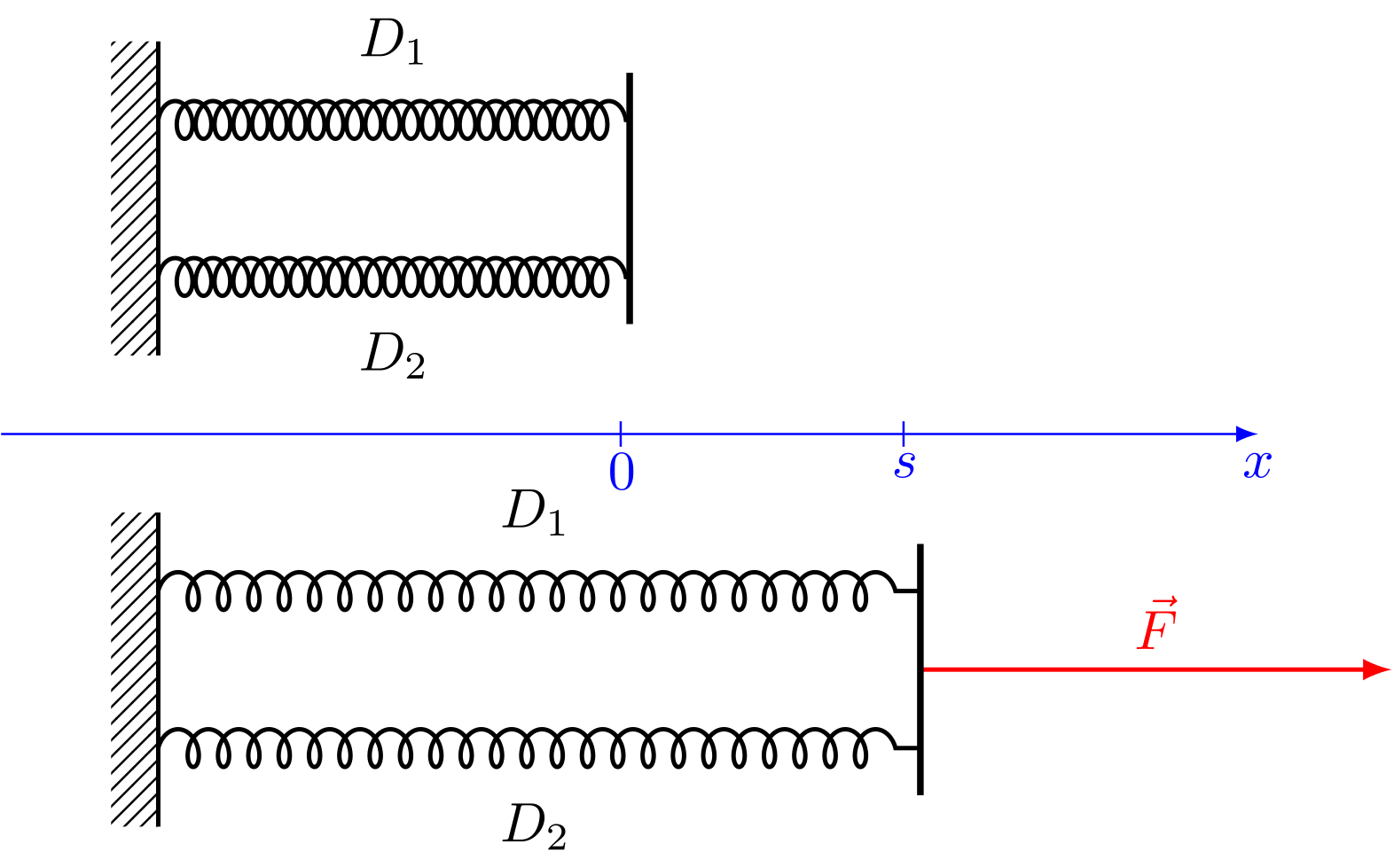
Abbildung 4.1.212: Parallelschaltung von Federn (C)
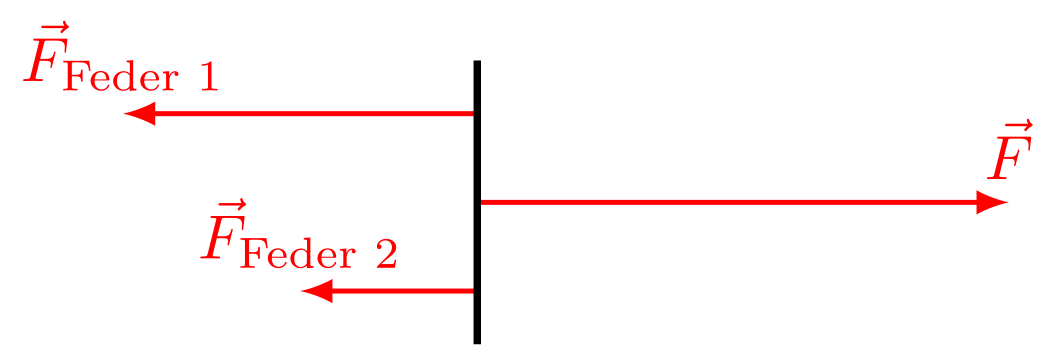
Abbildung 4.1.213: Kräfte in der Parallelschaltung von Federn (C)
Die Federkonstante des Gesamtsystems ergibt sich somit aus der Summe der beiden einzelnen Federkonstanten.
Skizze: Die Parallelschaltung zweier Federwaagen ist auch auf der folgenden interaktiven Skizze dargestellt. Im dabei entstehenden Graphen sieht man, dass sich die beiden Einzelkräfte der Federwaagen zu einer Gesamtkraft addieren. Daraus folgt, dass sich die Steigung des Graphen für das Gesamtsystem aus der Summe der Steigungen der Einzelfedern ergibt. Daher ist auch die Federkonstante des Gesamtsystems gleich der Summe der Federkonstanten der Einzelfedern.
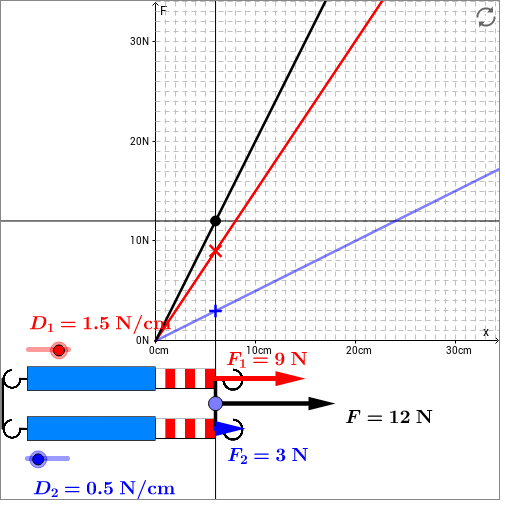
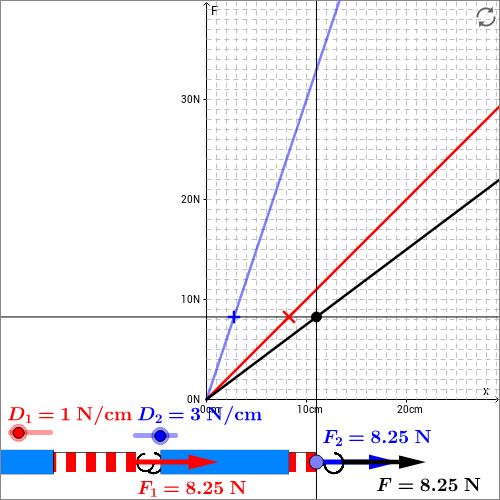
Serienschaltung von Federn (*)
Video 21: Serienschaltung von Federn (C)
.
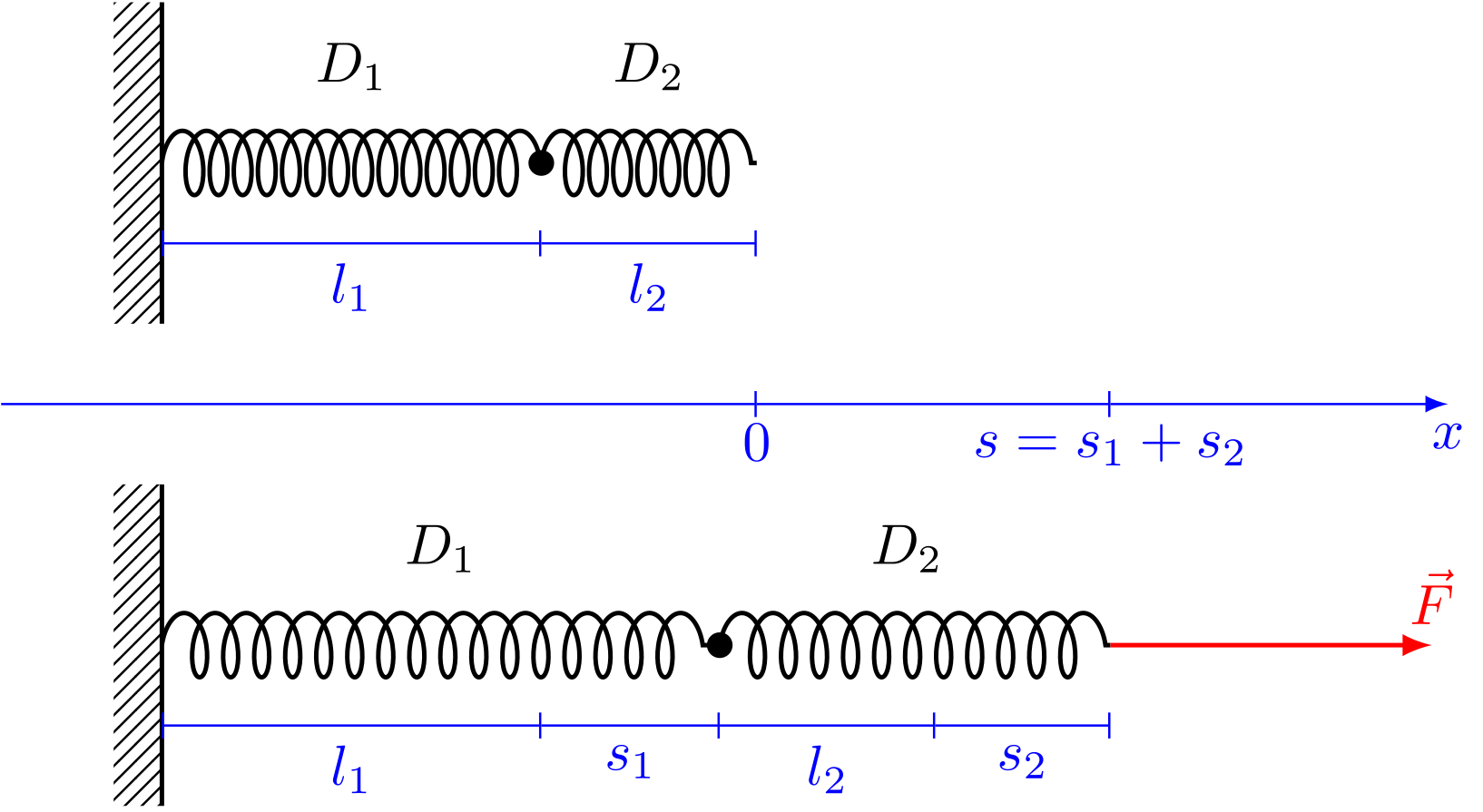
Abbildung 4.1.215: Serienschaltung von Federn (C)
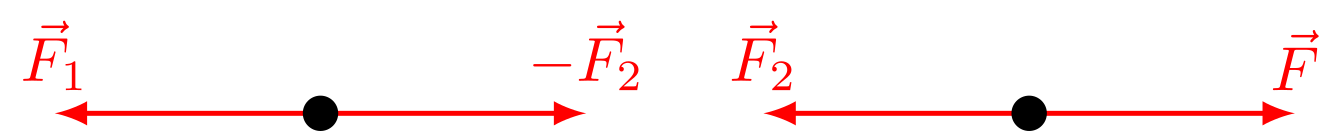
Abbildung 4.1.216: Kraft und Gegenkraft, die auf die Federn wirken (C)
Der Kehrwert der Federkonstanten des Gesamtsystems ist also die Summe der beiden Kehrwerte der einzelnen Federkonstanten.
Skizze: Die Serienschaltung zweier Federwaagen ist auch in der folgenden interaktiven Skizze dargestellt. Die Kraft, die auf jede einzelne Federwaage wirkt, hat den gleichen Wert und ist gerade die Gesamtkraft, mit der man am System zieht. Im dabei entstehenden Graphen sieht man, dass sich bei dieser Zugkraft die beiden Dehnungsstrecken der Federwaagen zu einer Gesamtdehnung addieren. Der größere Teil der Dehnung entfällt dabei auf die weichere der beiden Federn, also auf die mit der kleineren Federkonstanten. Untersuchen Sie dies, indem Sie die Federkonstanten der beiden Einzelfedern variieren.
Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie .
Falls nicht anders angegeben, verwenden Sie

