2. Elektromagnetismus
  3. Strom und Magnetismus
  4. Magnetisches Feld (!),(*),(+)

5.2.2 Magnetisches Feld





 

Noch kein Basiswissen vorhanden ...
Zu diesem Abschnitt gibt es leider noch kein Basiswissen.  

Magnetisches Feld (!)


Video 5: Das magnetische Feld (C) .



Aus der Mittelstufe und dem Alltag kennen Sie Magnetismus zunächst als ein unabhängiges Phänomen. Es gibt Permanentmagnete, Ferromagnete wie Eisen, dia- und paramagnetische Stoffe. Magnetische Felder haben einen Nord- und einen Südpol, analog zu elektrischen Feldern mit positiven und negativen Ladungen. Während man jedoch positive und negative Ladungen voneinander isolieren kann, ist es nicht möglich, einen isolierten Nord- oder Südpol zu erhalten. Magnetische Feldlinien sind immer geschlossen.

Video 6: Das Ampère'sche Kraftgesetz (C) .



Der französische Physiker André-Marie Ampère (1775–1836) fand heraus, dass zwei stromdurchflossene Leiter gegenseitig eine Kraft aufeinander ausüben. Auch der dänische Physiker Christian Oersted (1777–1851) hatte beobachtet, dass eine magnetische Kompassnadel durch einen stromdurchflossenen Leiter abgelenkt wird.

Strom und Magnetismus hängen also zusammen: Jeder stromdurchflossene Leiter ist von einem Magnetfeld umgeben. Dies kann man in einem Versuch z.B. mit Eisenfeilspänen sichtbar machen. Die Magnetfeldlinien sind ringförmig um den Leiter geschlossen. Die Orientierung ist durch die Rechte-Faust-Regel gegeben: Zeigt der Daumen in Richtung der sogenannten technischen Stromrichtung, also vom Pluspol zum Minuspol der Spannungsquelle, zeigen die Finger der rechten Hand die Richtung der Magnetfeldlinien an. Hier gibt es also keinen Nord- und keinen Südpol.

././Physikkurs/strommagnetisch_magnetfeld/images/strommagnetisch_leiterstueck_bfeld2.png
Abbildung 5.2.14: Magnetfeld um stromdurchflossenen Leiter (C)

   
././Physikkurs/strommagnetisch_magnetfeld/images/strommagnetisch_magnetfeld_rechte_faust_regel.png
Abbildung 5.2.15: Bestimmung der Richtung der Magnetfeldlinien (C)



Ampère hat die Kraftwirkung des Magnetfeldes und die Zusammenhänge mit den Eigenschaften des elektrischen Stroms untersucht und ein Kraftgesetz formuliert, das sogenannte Ampère’sche Kraftgesetz.

Eigenschaften der Kraft zwischen zwei parallelen stromdurchflossenen Leitern

  • Die Kraft ist umgekehrt proportional zum Abstand r der Leiter;

  • die Kraft ist proportional zu den elektrischen Strömen I1 und I2 ;

  • die Kraft wirkt anziehend bei gleicher Stromrichtung, abstoßend bei entgegengesetzter Stromrichtung;

  • die Kraft ist proportional zur Länge l der Leiter.



Ampère’sches Kraftgesetz  


F= μ0 2π   I1 · I2 r ·l ,  l= Leiterlänge  .

Analog zur elektrischen Feldkonstante ε0 verwendete auch Ampère eine Feldkonstante, nämlich die magnetische Feldkonstante μ0 , auch Vakuumpermeabilität genannt:

μ0 =4π· 10-7   V·s A·m  .



 

Das Magnetfeld eines (unendlich) langen, geraden Leiters (!)


Wir interpretieren das Kraftgesetz von Ampère,

F= μ0 2π   I1 · I2 r ·l ,

für die Kraft zwischen zwei langen stromdurchflossenen Leitern nun so, dass der Strom I1 ein Magnetfeld erzeugt, welches auf den Leiter mit dem Strom I2 eine Kraft ausübt.
Wir formen die Gleichung so um, dass auf der rechten Seite diejenigen Größen stehen, die das magnetische Feld von Leiter 1 charakterisieren:

F I2 ·l = μ0 2π · I1 r  .

Die so formulierten Eigenschaften des Magnetfeldes fasst man als magnetische Flussdichte B zusammen:

F I2 ·l =B  bzw.   | F → | I2 ·l =| B → | , | B → |=B= μ0 2π · I1 r  ,   B → = magnetische Flussdichte

Einheit von B:

[B]= V·s m2 = N A·m =T (Tesla) .



Wenn der Strom I1 in Leiter 1 ein Magnetfeld erzeugt, dann übt dieses also auf den Leiter 2 mit der Länge l im Abstand r die Kraft

F=B(r)· I2 ·l

aus, sobald der Leiter 2 vom Strom I2 durchflossen wird. Diese Kraft ist sowohl senkrecht zur Richtung des Stroms I2 als auch senkrecht zum Magnetfeld.

Dabei ist

B(r)= μ0 2π   I r

die magnetische Flussdichte eines langen geraden Leiters mit dem Strom I= I1 .
Das Magnetfeld ist also nicht homogen, sondern nimmt – analog zum elektrischen Feld der Punktladung – mit zunehmender Entfernung ab. Die Richtung des Magnetfeldes ergibt sich, wie oben erläutert, mit der Rechten-Faust-Regel.

Die interaktive GeoGebra-Skizze verdeutlicht noch einmal den Zusammenhang:

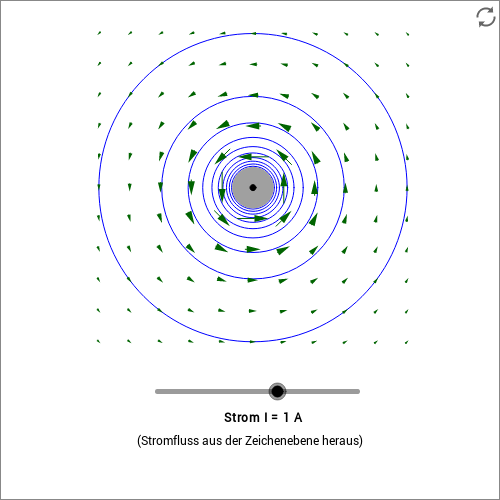
././Physikkurs/strommagnetisch_magnetfeld/images/geogebra_strommagnetisch_standbild3.png
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)

Der Leiter liegt hier senkrecht zur Zeichenebene, der Strom kommt aus der Zeichenebene heraus oder fließt in diese hinein.

Video 7: Das Magnetfeld eines langen Leiters (C) .



Beispiel 5.2.9  
  1. Gegeben seien zwei parallele Leiter mit I1 = I2 =1 A, Länge l=1 m, Abstand r=1 cm. Gesucht sind die magnetische Flussdichte B, die durch den Strom I1 im Abstand r erzeugt wird, und die Kraft F auf den zweiten Leiter.



    Zum Vergleich:

  2. 1 T sei die Flussdichte, die auf einen Leiter, der von 1 A durchflossen wird, auf einer Länge von 1 m eine Kraft von 1 N ausübt.

    Welchen Strom I1 bräuchte man im Abstand von 1 cm, um die Flussdichte 1 T zu erzeugen?





Zum Vergleich:

Am LHC beim Forschungszentrum CERN in Genf sind über 1000 Magnete im Einsatz, um die dort benötigten hohen Teilchenenergien zu erzeugen. Diese Magnete erreichen Felder von bis zu 7,7 T. Im sogenannten Hochfeld-Magnetlabor in Dresden werden Magnetfelder bis zu 100 T erzeugt. Dies sind mit die stärksten von Menschen erzeugten Magnetfelder. In Sonnen und insbesondere in Neutronensternen werden Felder von mehreren Tausend bis Millionen Tesla erreicht.

Video 8: Das Magnetfeld einer langen Spule (C) .



 

Magnetfeld einer langen Spule (+)


  1. Leiterschleife

    Das Magnetfeld eines langen, geraden Leiters wurde in der vorhergehenden Lektion vorgestellt. Es ist ein inhomogenes Feld. Nun biegen wir den Leiter zu einer Leiterschleife.

    Wie beim elektrischen Feld überlagern sich auch die Feldlinien des Magnetfelds im Inneren des Leiters. Für die magnetische Flussdichte im Mittelpunkt einer solchen Leiterschleife gilt:

    B= μ0   I 2r  ,  r= Radius der Leiterschleife  .



  2. Spule

    Hängt man nun viele solcher Leiterschleifen aneinander, erhält man eine elektromagnetische Spule:

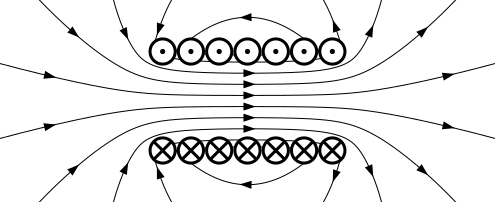    ././Physikkurs/strommagnetisch_magnetfeld/images/MFILE2xB-Feld_Solenoid.png
    Abbildung 5.2.17: Magnetfeld einer Spule (C)



    In Innenraum dieser Spule überlagern sich die Felder aller einzelnen Leiterschleifen so, dass ein (nahezu) homogenes Feld entlang der ganzen Spule entsteht. Dieses Feld ähnelt dem eines Stabmagneten. Nach Konvention sind die Feldlinien des äußeren Magnetfeldes vom Nordpol zum Südpol gerichtet, so dass unsere Beispielspule links einen Südpol ausbildet und rechts einen Nordpol.

    Ist der Radius der Spule sehr viel kleiner als die Länge der Spule, erhält man für die magnetische Flussdichte im Inneren einer langen Magnetspule:

    B= μ0   N·I l    für    r≪l .





Beispiel 5.2.10  
Eine Spule hat 600 Windungen. Die Länge der Spule beträgt 48 mm. Durch die Spule fließt ein Strom von 4,7 A. Damit herrscht im Inneren der Spule ein Magnetfeld von

B=4π· 10-7   V·s A·m · 600·4,7 A 0,0048 m =0,74 T .

Zum Vergleich: Das Erdmagnetfeld in Deutschland hat eine Flussdichte von B≈3· 10-5  T.


 

Magnetfeld mit Materie (*)


Video 9: Magnetfeld einer Spule mit Materie (C) .



In der Lektion über den Kondensator wurde gezeigt, dass das Einbringen von nichtleitender Materie in das elektrische Kondensatorfeld die Kapazität des Kondensators beeinflusst.

Auch in eine Spule kann man Materie einbringen. Dabei gibt es unterschiedliche magnetische Eigenschaften. Bei paramagnetischen Stoffen kann man sich vorstellen, dass das Material aus vielen ungeordneten Elementarmagneten besteht. Kommt das Material in ein Magnetfeld, so ordnen sich die Elementarmagnete in Richtung der magnetischen Feldlinien so an, dass das äußere Magnetfeld verstärkt wird. Beim Ferromagnetismus neigen die Elementarmagnete selbst dazu, sich parallel auszurichten. Dadurch verstärken sie ein äußeres Magnetfeld viel stärker als bei paramagnetischen Stoffen. Nimmt man das äußere Magnetfeld weg, so bleiben einige Elementarmagnete ausgerichtet, es bleibt ein Restmagnetfeld zurück. Das nennt man Remanenz.

Diamagnetische Stoffe bestehen aus Atomen oder Molekülen, die kein permanentes magnetisches Dipolmoment, also keine Elementarmagnete besitzen. Erst bei Anlegen eines Magnetfeldes werden magnetische Dipole induziert, die sich dann aber entgegen den äußeren magnetischen Feldlinien ausrichten und somit das Magnetfeld schwächen. Diese Schwächung ist ein Analogon zur Schwächung des elektrischen Feldes in einem Kondensator durch ein Dielektrikum.

Spule mit Materie  
Die Wirkung von Materie im Magnetfeld wird, auch wieder analog zur Wirkung des Dielektrikums, mit einer materialabhängigen Konstanten, der sogenannten Permeabilitätszahl μ r beschrieben:

B= μ r · μ0   N·I l  .

Es gilt:
μ r <1:
diamagnetisches Material (Beispiel Kupfer, μ r =0,9999904);
μ r >1:
paramagnetisches Material (Beispiel Aluminium, μ r =1,000021);
μ r ≫1:
ferromagnetisches Material (Beispiel Eisen, μ r =300– 1000).
Daraus sieht man, dass ferromagnetisches Material das Magnetfeld in einer Spule deutlich erhöhen kann. Dielektrika dagegen können niemals ein elektrisches Feld verstärken.




Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Verwenden Sie e=1,602 · 10-19   C und μ0 =4π · 10-7   T m A  .