2. Mechanik
  3. Kräfte und ihre Wirkungen
  4. Newtonsche Axiome (!)

4.1.8 Newtonsche Axiome





 

Noch kein Basiswissen vorhanden ...
Zu diesem Abschnitt gibt es leider noch kein Basiswissen.

Wie sich Kräfte auf die Bewegung und die Bewegungsänderung von Körpern auswirken, kann mit Newtons drei Axiomen beschrieben werden. Sie werden im Folgenden jeweils als Aussagesatz und als physikalische Formel dargestellt. Zusätzlich ist jeweils ein von der ESA produziertes erklärendes Video angegeben.

Auf die in den Axiomen auftretenden Größen Geschwindigkeit und Beschleunigung werden wir später im gleichnamigen Abschnitt 4.2.1 näher eingehen.

 

1. Axiom: Trägheitsprinzip (!)
Ein Körper mit konstanter Masse, auf den keine Kraft einwirkt, bleibt in Ruhe oder bewegt sich geradlinig gleichförmig weiter.

    F → =0  ⇔   v → · =0   



 

2. Axiom: Aktionsprinzip (!)
Ein Körper mit konstanter Masse m, auf den eine äußere Kraft wirkt, wird in Richtung der Kraft beschleunigt. Die Beschleunigung ist proportional zur Größe der Kraft und antiproportional zur Masse.

    F → =m  a →    



 

3. Axiom: Reaktionsprinzip (!)
Die Kräfte, die zwei Körper aufeinander ausüben, sind vom Betrag her gleich groß und zeigen in entgegengesetzte Richtungen.

    F → 12 =- F → 21    







Skizze: In der folgenden Skizze sollen die Aussagen von Newtons Axiomen näher untersucht werden.

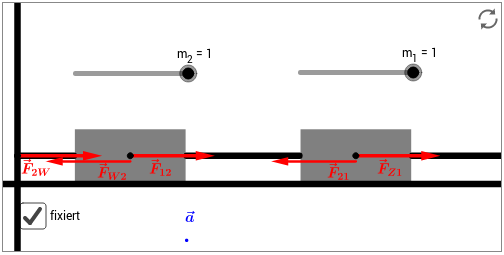
././Physikkurs/kraefte_newton/images/geogebra_standbild14.png
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)

Durch das Zugseil wirkt auf den Körper 1 (rechter Körper) eine nach rechts ziehende Kraft F → Z 1 . Diese Kraft wird über ein Verbindungsseil auf Körper 2 (linker Körper) übertragen ( F → 12 ). Gemäß dem Reaktionsprinzip (3. Axiom) zieht der Körper 2 mit der gleichen, aber entgegengesetzten Kraft F → 21 an Körper 1. Die Kraft wird weiter auf die Wand übertragen ( F → 2 W ). Auch diese wirkt mit der gleichen, aber entgegengesetzten Kraft auf Körper 2 ( F → W 2 ).

Da die Kräfte sich bei beiden Körpern ausgleichen, ist die Gesamtkraft bei jedem der zwei Körper gleich null. Gemäß dem Trägheitsprinzip (1. Axiom) bleiben die Körper daher in Ruhe.

Entfernen Sie nun den Haken „fixiert“. Dadurch wird eine Situation gezeigt, bei der die Anbindung an die linke Wand nicht existiert. Gemäß dem Aktionsprinzip (2. Axiom) entsteht jetzt eine Beschleunigung a der beiden Körper von

a= F Z 1 m1 + m2  .

Da ein Teil der auf Körper 1 wirkenden Kraft durch die Beschleunigung „absorbiert“ wird, reduziert sich die Kraft, die über das Verbindungsseil auf Körper 2 wirkt, gegenüber dem statischen Fall:

F12 = F Z 1 - m1  a .

Der Körper 2 wird also mit der Kraft F12 beschleunigt und man erhält als Beschleunigung
 
a2 = F Z 1 - m1  a m2 ​ = ( m1 + m2 ) a- m1  a m2 ​ =a .
 
Betrachtet man den Körper 1 alleine, erhält man ebenfalls
 
a1 = F Z 1 - F21 m1 ​ = F12 + m1  a- F21 m1 ​ =a .
 
Variieren Sie nun die Massen der beiden Körper und beobachten Sie die Veränderungen an den Kräften.

Beispiel 4.1.73  
Ein PKW der Masse m P =1,5 t zieht einen Anhänger der Masse m A =0,5 t. Der PKW überträgt eine Kraft von F=4 kN auf die Straße. Wie groß ist die Beschleunigung des Gespanns und welche Kraft wirkt auf die Kupplung zwischen PKW und Anhänger?

Als Beschleunigung erhält man
 
a= F m P + m A ​ = 4000 N 2000 kg ​ =2  m s2  .
 
Die Kraft auf die Kupplung beträgt
 
F K = m A  a ​ =500 kg·2  m s2 ​ =1 kN .
 




Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie g=9,81  m s2  .