5.3.3 Kondensatoren
Video 8: Reihen- und Parallelschaltung von Kondensatoren (C)
.
In Abschnitt 5.1.4 haben wir schon den (Platten-)Kondensator kennengelernt. Der Kondensator kann Ladungen aufnehmen, dabei bildet sich eine Spannung zwischen seinen beiden Flächen (Elektroden), die – mit der Kapazität des Kondensators als Proportionalitätsfaktor – proportional zu der aufgenommenen Ladung ist:
Die Einheit der Kapazität ist das Farad (). Das Schaltzeichen des Kondensators ist:
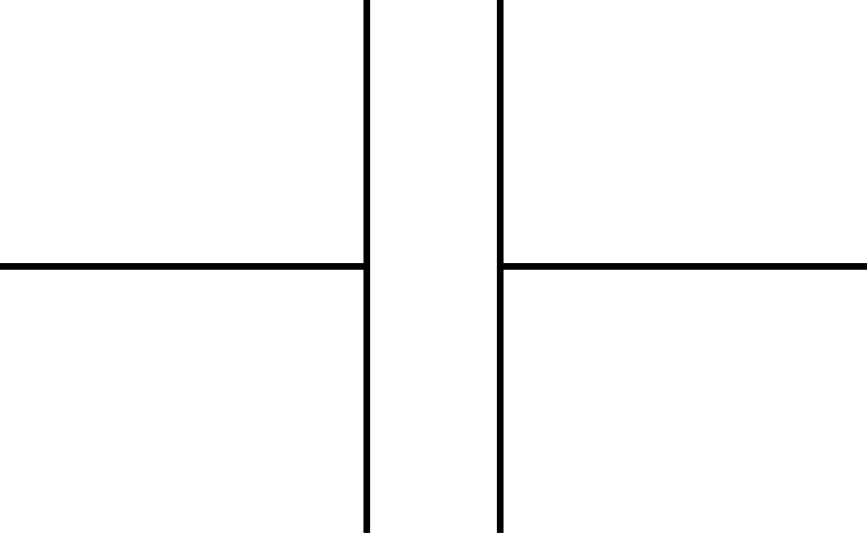
Wir betrachten zunächst nur den elektrostatischen Fall, d.h. der Kondensator ist mit der Ladung aufgeladen, es liegt die konstante Spannung an. Ein- und Ausschaltvorgänge sowie Wechselspannung behandeln wir weiter unten.
Parallelschaltung (+)
Die folgende Skizze zeigt eine Parallelschaltung von Kondensatoren.
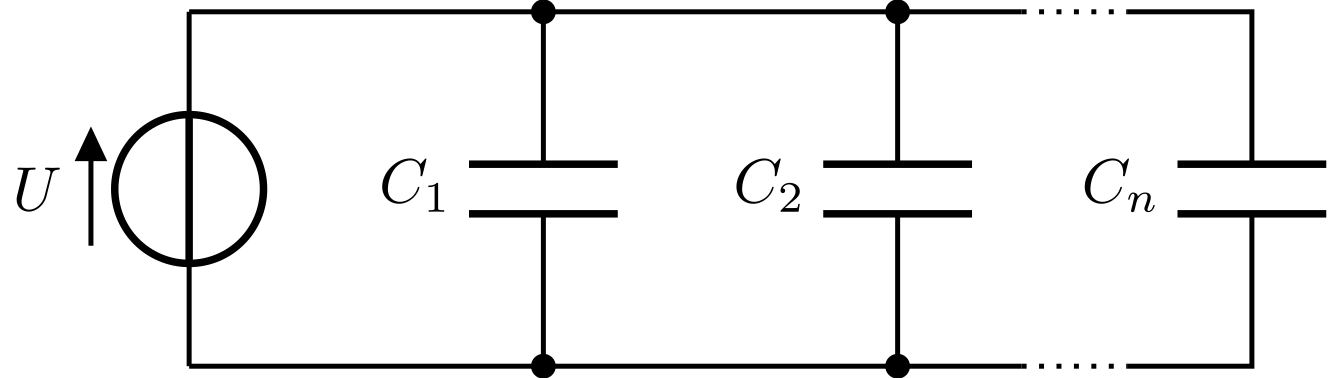
Bei der Parallelschaltung liegt an allen Kondensatoren die gleiche Spannung an. Die Gesamtladung wird auf die Einzelkondensatoren so verteilt, dass sie jeweils mit der Ladung aufgeladen werden:
Damit ergibt sich für die Gesamtkapazität :
Reihenschaltung (+)
In folgender Skizze ist die Reihenschaltung von Kondensatoren dargestellt:
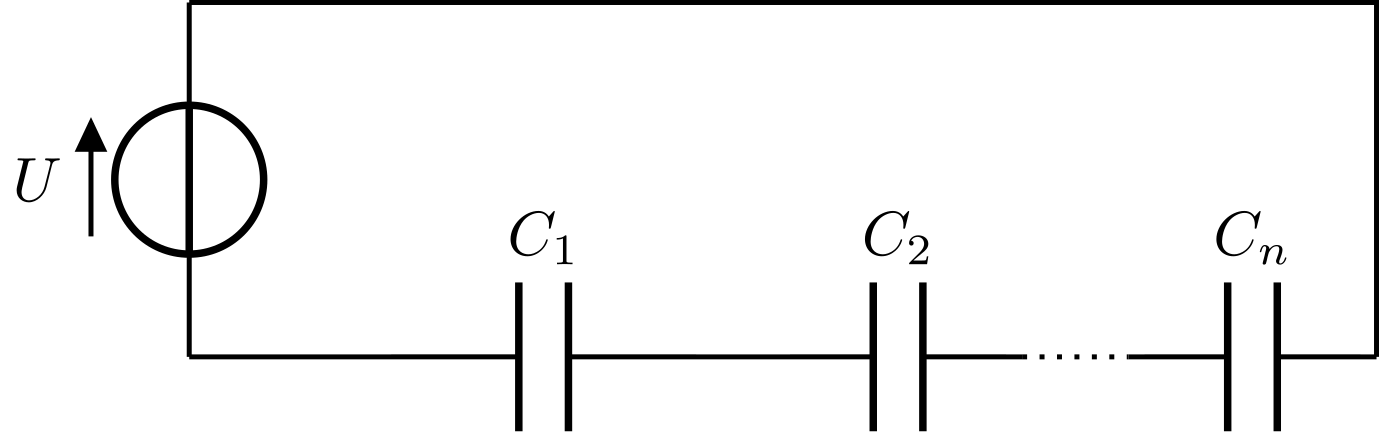
Im Fall der Reihenschaltung befinden sich alle Kondensatoren in einer gemeinsamen Masche. Darüber hinaus werden die Kondensatoren alle mit der gleichen Stromstärke geladen, d.h. jeder der Kondensatoren besitzt die gleiche Ladung . Gemäß der Maschenregel muss die Summe der Einzelspannungen an den Kondensatoren gerade gleich der Spannung der Spannungsquelle sein. Es ergibt sich also:
Damit erhält man für die Gesamtkapazität :
Die Einheit der Kapazität ist das Farad (). Das Schaltzeichen des Kondensators ist:

Abbildung 5.3.76: Schaltzeichen eines Kondensators (C)
Wir betrachten zunächst nur den elektrostatischen Fall, d.h. der Kondensator ist mit der Ladung aufgeladen, es liegt die konstante Spannung an. Ein- und Ausschaltvorgänge sowie Wechselspannung behandeln wir weiter unten.
Parallelschaltung (+)
Die folgende Skizze zeigt eine Parallelschaltung von Kondensatoren.

Abbildung 5.3.77: Parallelschaltung von Kondensatoren (C)
Bei der Parallelschaltung liegt an allen Kondensatoren die gleiche Spannung an. Die Gesamtladung wird auf die Einzelkondensatoren so verteilt, dass sie jeweils mit der Ladung aufgeladen werden:
Damit ergibt sich für die Gesamtkapazität :
Die Kapazität einer Parallelschaltung von Kondensatoren ist gleich der Summe der Einzelkapazitäten:
Beispiel
5.3.14
Ein -Kondensator und ein -Kondensator werden parallel geschaltet.
Bei der Parallelschaltung von Kondensatoren ergibt sich die Gesamtkapazität als Summe der Einzelkapazitäten. Damit gilt
Die Gesamtkapazität der Schaltung beträgt also .
Ein -Kondensator und ein -Kondensator werden parallel geschaltet.
Bei der Parallelschaltung von Kondensatoren ergibt sich die Gesamtkapazität als Summe der Einzelkapazitäten. Damit gilt
Die Gesamtkapazität der Schaltung beträgt also .
Reihenschaltung (+)
In folgender Skizze ist die Reihenschaltung von Kondensatoren dargestellt:

Abbildung 5.3.78: Reihenschaltung von Kondensatoren (C)
Im Fall der Reihenschaltung befinden sich alle Kondensatoren in einer gemeinsamen Masche. Darüber hinaus werden die Kondensatoren alle mit der gleichen Stromstärke geladen, d.h. jeder der Kondensatoren besitzt die gleiche Ladung . Gemäß der Maschenregel muss die Summe der Einzelspannungen an den Kondensatoren gerade gleich der Spannung der Spannungsquelle sein. Es ergibt sich also:
Damit erhält man für die Gesamtkapazität :
Der Kehrwert der Gesamtkapazität einer Reihenschaltung von Kondensatoren ist gleich der Summe der Kehrwerte der Einzelkapazitäten,
Beispiel
5.3.15
Drei -Kondensatoren werden in Reihe geschaltet.
Bei der Reihenschaltung von Kondensatoren ist der Kehrwert der Gesamtkapazität gegeben als Summe der Kehrwerte der Einzelkapazitäten. Mit gilt hier
Schließlich muss davon noch der Kehrwert gebildet werden und mal erhält
Die Gesamtkapazität der Schaltung beträgt also .
Drei -Kondensatoren werden in Reihe geschaltet.
Bei der Reihenschaltung von Kondensatoren ist der Kehrwert der Gesamtkapazität gegeben als Summe der Kehrwerte der Einzelkapazitäten. Mit gilt hier
Schließlich muss davon noch der Kehrwert gebildet werden und mal erhält
Die Gesamtkapazität der Schaltung beträgt also .
Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.

