5.1.1 Elektrische Ladung
Basiswissen – Aufbau der Atome
Für ein besseres Verständnis, was eine elektrische Ladung ist, schauen wir uns erst den Aufbau der Materie an.
Alles was uns umgibt, ist aus sogenannten Atomen aufgebaut. Diese Atome bestehen aus einem Kern und einer Hülle. Der Kern besteht aus kleinen Teilchen, den sogenannten Protonen und Neutronen. Um den Kern bewegen sich Elektronen und bilden die Hülle. In einem Atom sind immer gleich viele Protonen wie Elektronen enthalten.
Protonen und Neutronen sind nahezu gleich schwer. Elektronen besitzen sehr viel weniger Masse als Protonen und Neutronen.
Neben der unterschiedlichen Masse haben Elektronen und Protonen eine weitere Eigenschaft. Sie tragen eine sogenannte elektrische Ladung. Die Ladung der Protonen wird als positiv und die Ladung der Elektronen als negativ bezeichnet. Neutronen tragen keine Ladung. Sie sind elektrisch neutral.
- Die kleinste Ladungseinheit wird Elementarladung genannt.
- Ein Elektron trägt genau eine negative Elementarladung .
- Ein Proton trägt genau eine positive Elementarladung .
- Das Symbol für Ladungen ist .
- Die Einheit der Ladung heißt Coulomb, .
| Teilchenart | Ladung | Masse |
| Elektron | () | |
| Proton | () | |
| Neutron | keine Ladung |
Eines der ersten Modelle, die den Aufbau von Atomen beschreiben, wurde 1913 von Niels Bohr entwickelt. Er ging davon aus, dass sich die negativ geladenen Elektronen (
 )
auf geschlossenen Bahnen um die Protonen
(
)
auf geschlossenen Bahnen um die Protonen
(
 )
und Neutronen
(
)
und Neutronen
(
 )
des Atomkerns bewegen, ähnlich wie sich die Planeten um die Sonne bewegen.
)
des Atomkerns bewegen, ähnlich wie sich die Planeten um die Sonne bewegen. Die Anzahl der Protonen und Elektronen bestimmt, um welches Element es sich handelt. Ein Atom besitzt die gleiche Anzahl von Elektronen wie Protonen. Es trägt also gleich viele positive wie negative Ladungen und ist von außen betrachtet elektrisch neutral.
Die ersten Atome im Periodensystem der Elemente, Wasserstoff (links), Helium (Mitte) und Lithium (rechts), sind in der einfachen Skizze dargestellt:
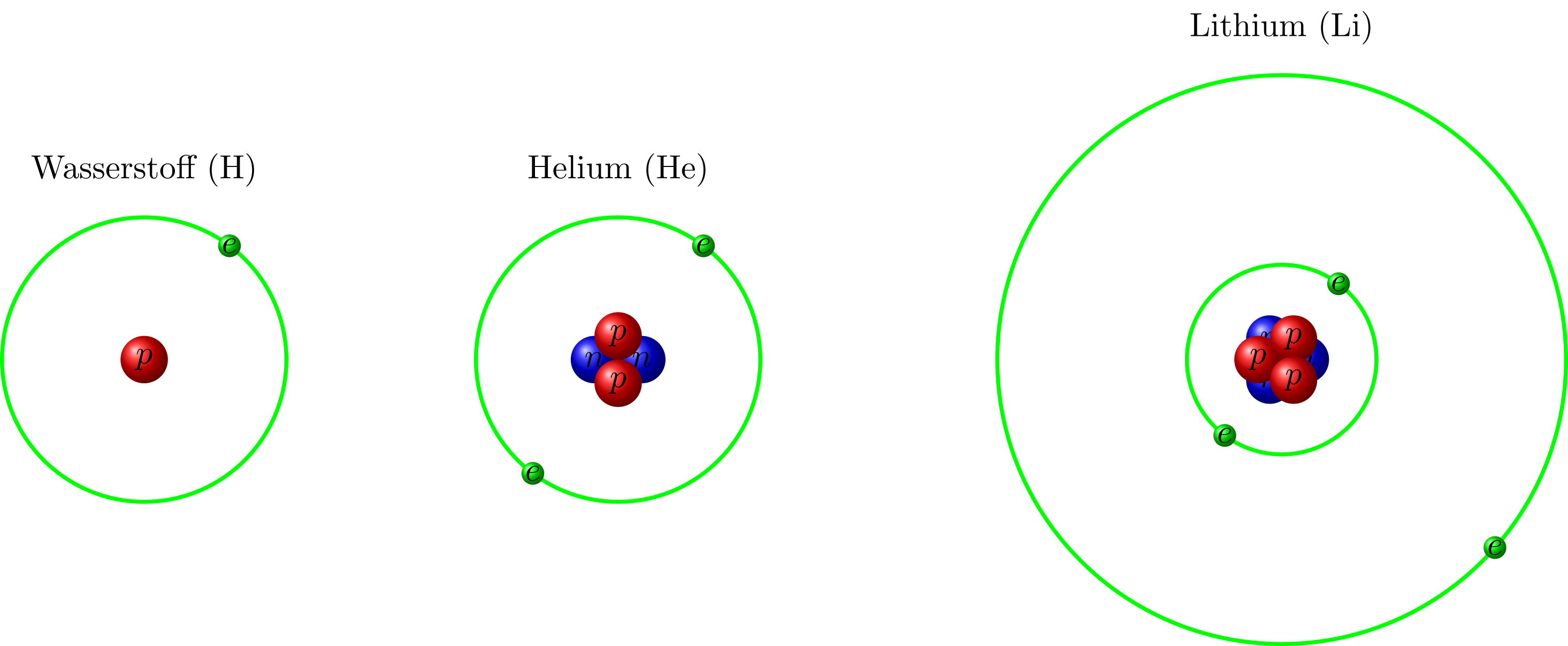
Abbildung 5.1.4: Vereinfachte Darstellung von Wasserstoff, Helium und Lithium im Bohrschen Atommodell (C)
Um eine erste Vorstellung zu erhalten, ist dieses einfache Modell ausreichend. Für die verschiedenen existierenden Elemente wurden von Mendelejew und Mayer unabhängig voneinander das Periodensystem der Elemente entwickelt. Darin sind die Atome mit ihrem Namen, der zugehörigen Abkürzung und weiteren Größen aufgeführt.
Die verschiedenen Atome können sich zu sogenannten Molekülen verbinden und bilden so die gesamte uns umgebende Materie.
Wie schon erwähnt wurde, sind Atome und auch Moleküle elektrisch neutral. Jedoch ist es möglich elektrische Ladungen zu trennen. Das können Sie selbst ausprobieren. Nehmen Sie ein Plastiklineal und reiben es fest an einem Tuch oder Pullover. Nähern Sie das Lineal an kleine Papierschnipsel an, bewegen sich die Papierschnipsel auf das Lineal zu und bleiben daran haften. Das ist keine Zauberei, sondern kann mit der Trennung von Ladungen erklärt werden. Durch das Reiben des Lineals am Stoff, wandern Ladungen von einem Körper zum andern. Das Lineal trägt eine andere Ladung als das Tuch. Die Ladung auf dem Lineal wirkt anziehend auf die Papierschnipsel.
Beispiel
5.1.1
Wieviele Elektronen ergeben eine Ladung von ?
Die Anzahl der Elektronen ergibt sich, wenn die Ladung durch die Ladung , die ein Elektron trägt, geteilt wird:
Wieviele Elektronen ergeben eine Ladung von ?
Die Anzahl der Elektronen ergibt sich, wenn die Ladung durch die Ladung , die ein Elektron trägt, geteilt wird:
Ladungen üben Kräfte aus. Gleichnamige Ladungen stoßen sich ab und ungleichnamige Ladungen ziehen sich an:
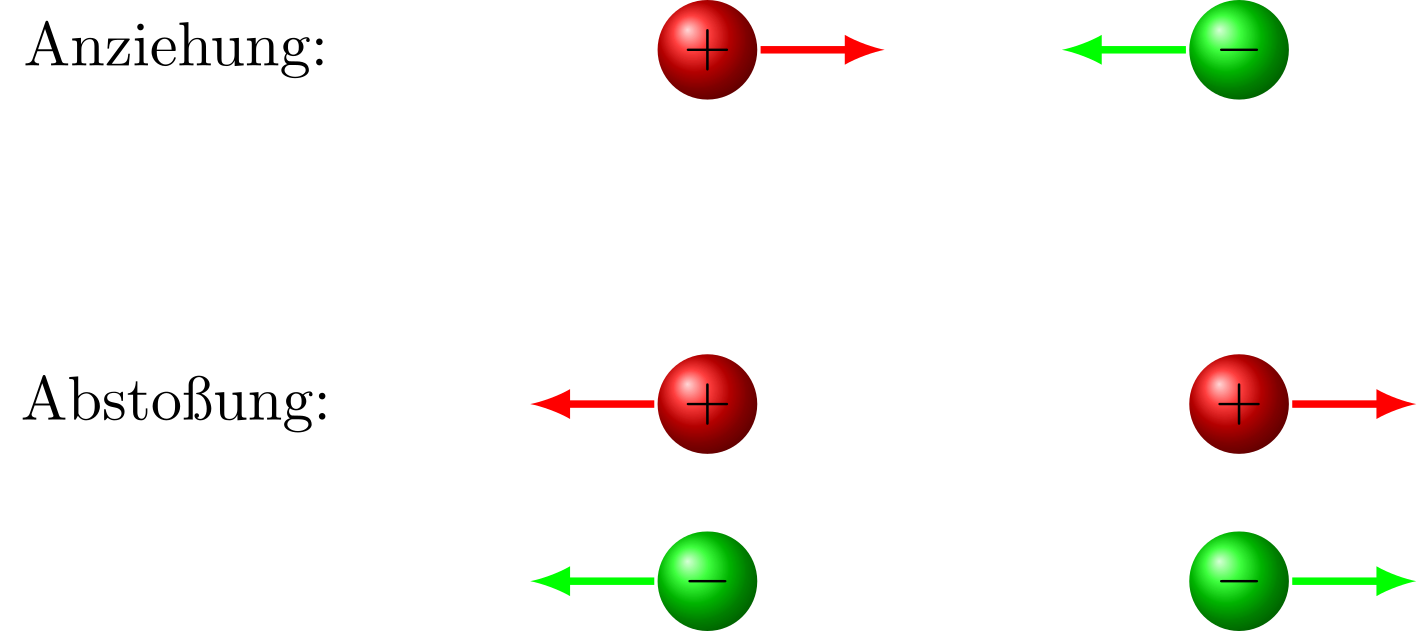

Abbildung 5.1.5: Anziehende und abstoßende Wirkung der elektrisch geladenen Teilchen aufeinander (C)
Bei der Ladungstrennung werden Elektronen aus dem Atomverband gelöst und wandern von einem Körper zum Körper . Körper besitzt dann mehr negative Ladungen und ist negativ aufgeladen. Gleichzeitig fehlen diese negativen Ladungen Körper . ist positiv geladen. Ein Atom oder Molekül, dem ein oder mehrere Elektronen fehlen oder mehr Elektronen als Protonen hat, wird Ion genannt. Ladungen können getrennt werden. Es ist jedoch nicht möglich, Ladungen zu erzeugen oder zu vernichten.
Für zwei punktförmige, geladene Körper kann die anziehende oder abstoßende Kraft durch das Coulomb-Gesetz beschrieben werden:
Dabei gilt:
Dabei gilt:
- , : sind die Ladungen der Körper,
- : ist der Abstand zwischen den Ladungen,
- : heißt elektrische Feldkonstante oder Dielektrizitätskonstante des Vakuums mit
- : heißt Permittivitätszahl und ist eine Stoffkonstante. Sie berücksichtigt den Einfluss des Mediums, in dem sich die beiden Körper befinden. Im Vakuum gilt und in Luft .
Diese Formel kann in guter Näherung auch für jeweils räumlich eng begrenzte Ladungsverteilungen angewendet werden, wenn deren Ausdehnungen sehr klein im Vergleich zu ihrem Abstand sind. Als Abstand der Ladungsverteilungen wird dann der Abstand der Ladungsmittelpunkte verwendet.
Beispiel
5.1.2
Zwei Punktladungen mit und befinden sich im Abstand voneinander. Welche Kraft üben sie aufeinander aus, wenn sich die beiden Ladungen im Vakuum befinden?
Die beiden Ladungen stoßen sich ab, da beide positiv sind. Diese Kraft wird mit dem coulombschen Gesetz berechnet:
Zwei Punktladungen mit und befinden sich im Abstand voneinander. Welche Kraft üben sie aufeinander aus, wenn sich die beiden Ladungen im Vakuum befinden?
Die beiden Ladungen stoßen sich ab, da beide positiv sind. Diese Kraft wird mit dem coulombschen Gesetz berechnet:
Beispiel
5.1.3
In welchem Abstand befinden sich zwei Punktladungen mit und , wenn zwischen ihnen eine Kraft wirkt und das Umgebungsmedium Luft ist?
Zur Beantwortung der Frage muss das Coulomb-Gesetz nach dem Abstand umgeformt werden:
In welchem Abstand befinden sich zwei Punktladungen mit und , wenn zwischen ihnen eine Kraft wirkt und das Umgebungsmedium Luft ist?
Zur Beantwortung der Frage muss das Coulomb-Gesetz nach dem Abstand umgeformt werden:
- Es gibt positive und negative Ladung.
- Ladungen üben Kräfte aufeinander aus.
- Ein Körper mit gleich vielen positiven und negativen Ladungen ist elektrisch neutral.
- Ladungen können getrennt, aber nicht erzeugt oder vernichtet werden.
Aufgabe 5.1.4
Welche Aussagen über Protonen, Neutronen und Elektronen sind richtig?
Welche Aussagen über Protonen, Neutronen und Elektronen sind richtig?
| Elektronen, Protonen und Neutronen verteilen sich gleichmäßig im gesamten Atomvolumen. | |
| Elektronen sind sehr viel leichter als Protonen. | |
| Nahezu die gesamte Masse eines Atoms sitzt im Kern. | |
| Neutronen sind leichter als Elektronen. | |
| Elektronen und Protonen haben ungefähr die gleichen Masse. | |
| In einem Atom haben Elektronen und Kern die gleiche Masse. |
Aufgabe 5.1.5
Eine Kugel wird mit einer Ladung aufgeladen.
Wie und um welche Zahl ändert sich die Anzahl der Elementarteilchen?

Eine Kugel wird mit einer Ladung aufgeladen.
Wie und um welche Zahl ändert sich die Anzahl der Elementarteilchen?
Aufgabe 5.1.6
Welche der Formeln beschreibt die Coulomb-Kraft zwischen zwei punktförmigen Ladungen und richtig?
Welche der Formeln beschreibt die Coulomb-Kraft zwischen zwei punktförmigen Ladungen und richtig?
Aufgabe 5.1.7
Wie verändert sich die Coulomb-Kraft zwischen zwei punktförmigen Ladungen und , wenn der Abstand halbiert wird?
Wie verändert sich die Coulomb-Kraft zwischen zwei punktförmigen Ladungen und , wenn der Abstand halbiert wird?
Aufgabe 5.1.8
Warum stehen nach dem Ausziehen einer Mütze die Haare in alle Richtungen ab?
Normalerweise ist in einem Körper die Anzahl der positiven Ladungen der Anzahl negativen Ladungen. Beim Absetzen der Mütze findet durch Reibung statt. Die Haare werden dabei aufgeladen. Die Haare stoßen sich aufgrund der Ladung ab.
Warum stehen nach dem Ausziehen einer Mütze die Haare in alle Richtungen ab?
Normalerweise ist in einem Körper die Anzahl der positiven Ladungen der Anzahl negativen Ladungen. Beim Absetzen der Mütze findet durch Reibung statt. Die Haare werden dabei aufgeladen. Die Haare stoßen sich aufgrund der Ladung ab.
Aufgabe 5.1.9
Zwei Kugeln sind voneinander entfernt. Auf der ersten Kugel befindet sich die Ladung . Die zweite Kugel trägt die Ladung . Welchen Betrag hat die zwischen Kugel wirkende Kraft? Ist die Kraft abstoßend oder anziehend?
E
Die beiden Kugeln
Zwei Kugeln sind voneinander entfernt. Auf der ersten Kugel befindet sich die Ladung . Die zweite Kugel trägt die Ladung . Welchen Betrag hat die zwischen Kugel wirkende Kraft? Ist die Kraft abstoßend oder anziehend?
E
Die beiden Kugeln
Aufgabe 5.1.10
Auf einer Kugel befindet sich die Ladung . Eine zweite identische Kugel trägt die Ladung . Die Kugeln berühren sich kurzzeitig und werden dann im Abstand voneinander aufgestellt.
Wie ist die Kraft zwischen den beiden Kugeln?
E
Auf einer Kugel befindet sich die Ladung . Eine zweite identische Kugel trägt die Ladung . Die Kugeln berühren sich kurzzeitig und werden dann im Abstand voneinander aufgestellt.
Wie ist die Kraft zwischen den beiden Kugeln?
E
Die elektrische Ladung (!)
Video 1: Elektrische Ladung (C)
.
Video 2: Aufbau der Materie und Elementarladung (C)
.
Materie ist aus Atomen aufgebaut. Die Atomkerne bestehen aus positiv geladenen Protonen und elektrisch neutralen Neutronen, während in der Atomhülle negativ geladene Elektronen vorhanden sind. Interessanterweise ist die Ladung eines Protons und eines Elektrons vom Betrag her genau gleich. Ein Atom besitzt gleich viele Elektronen wie Protonen und ist deshalb als Gesamtsystem ungeladen. Daher ist gewöhnliche Materie elektrisch neutral. Atome mit unterschiedlicher Anzahl von Protonen und Elektronen werden als Ionen bezeichnet.
Den Betrag der elektrischen Ladung von Proton bzw. Elektron nennt man die Elementarladung . Sie wird/wurde zum 20. Mai 2019 auf den Wert
festgelegt, womit das Coulomb seinerseits den Wert erhält. Die Elementarladung ist gleichzeitig die kleinste Ladungseinheit von frei existierenden Teilchen. Ist ein Körper elektrisch negativ geladen, so besitzt er einen Überschuss an Elektronen. Ist er positiv geladen, so hat er einen Elektronenmangel. Der Transport von elektrischer Ladung findet in Festkörpern typischerweise durch Elektronen statt, da die Atomkerne, in denen sich die Protonen befinden, an festen Positionen befinden. Die Bewegung von elektrischen Ladungen nennt man den elektrischen Strom.
Bildet ein Körper ein abgeschlossenes System, können keine elektrischen Ladungen vom Körper entfernt oder dem Körper hinzugefügt werden. In einem abgeschlossenen System ist die Gesamtladung konstant. Damit haben wir neben Energie- und Impulserhaltung aus der Mechanik einen weiteren Erhaltungssatz kennengelernt, nämlich den der Ladungserhaltung. Allerdings können innerhalb eines abgeschlossenen Systems elektrische Ladungen verschoben werden, zum Beispiel durch Influenz, ohne dass dabei seine Gesamtladung verändert wird.
Das coulombsche Gesetz (!)
Video 3: Das coulombsche Gesetz (C)
.
Gleichnamig geladene Körper stoßen sich gegenseitig ab ( bzw. ), ungleichnamig geladene Körper ziehen sich an ( bzw. ).
Die Kraftwirkung ist proportional zur Ladungsmenge auf dem ersten Körper , der Ladungsmenge auf dem zweiten Körper
und umgekehrt proportional zum Quadrat des Abstands zwischen beiden Körpern.
Dies wird durch das coulombsche Kraftgesetz beschrieben:
Die Konstante heißt Dielektrizitätskonstante des Vakuums und besitzt den Wert
Die Konstante heißt Dielektrizitätskonstante des Vakuums und besitzt den Wert
Exakt gilt das coulombsche Kraftgesetz nur für Punktladungen, also für den Fall, dass die beiden Ladungen jeweils auf einen Punkt konzentriert sind.
In der folgenden animierten Skizze können zwei Ladungen beliebig in der Ebene verschoben werden. Auch die Ladungsmenge und das Ladungsvorzeichen der beiden Ladungen können variiert werden. Die auf die beiden Ladungen wirkenden Kräfte durch die elektrische Anziehung bzw. Abstoßung werden jeweils angezeigt.
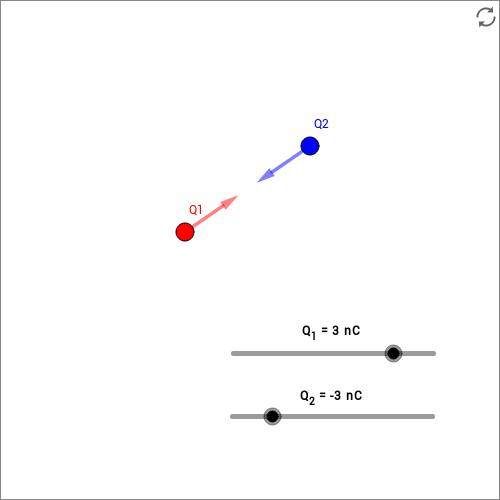
Video 4: Beispiele zur Berechnung der Coulomb-Kraft (C)
.
Beispiel
5.1.11
- Gegeben sind die Punktladungen sowie der Abstand der beiden Ladungen mit .
Berechnen Sie die Coulomb-Kraft.
-
Bestimmen Sie die elektrische Anziehungskraft zwischen einem Elektron und einem Proton im Atom.
Gegeben ist der Abstand der Teilchen .
Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Verwenden Sie und .
Verwenden Sie und .

