8.1.2 Die Wellenfunktion
Basiswissen „Wellenfunktion “
Findet die Störung nicht nur einmal statt, sondern wiederholt sich periodisch, führt dies auch zu einer periodischen Ausbreitung der Störung. Im folgenden sollen die Begriffe Wellenlänge, Frequenz und Amplitude für eine transversale Welle am Beispiel einer periodischen Anregung eingeführt werden. Bei einer transversalen Welle schwingt der Erreger senkrecht zur Ausbreitungsrichtung der Welle.
Der Erreger soll eine Sinusschwingung ausführen. Das bedeutet, dass die Auslenkung () des Erregers von seiner Ruhelage in Abhängigkeit von der Zeit mit einer Sinusfunktion beschrieben werden kann:
Auch hier gilt die Beziehung zwischen der Frequenz einer Schwingung deren Schwingungsdauer .
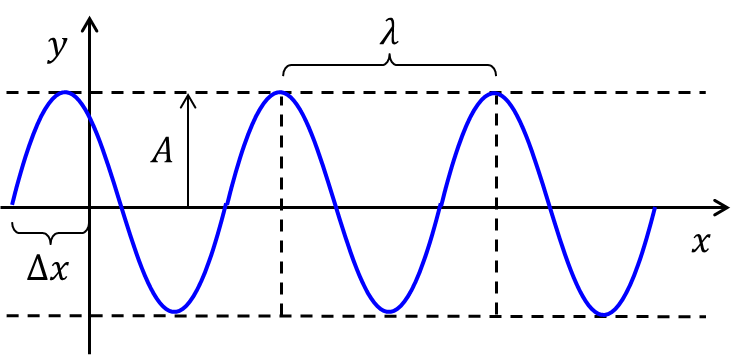
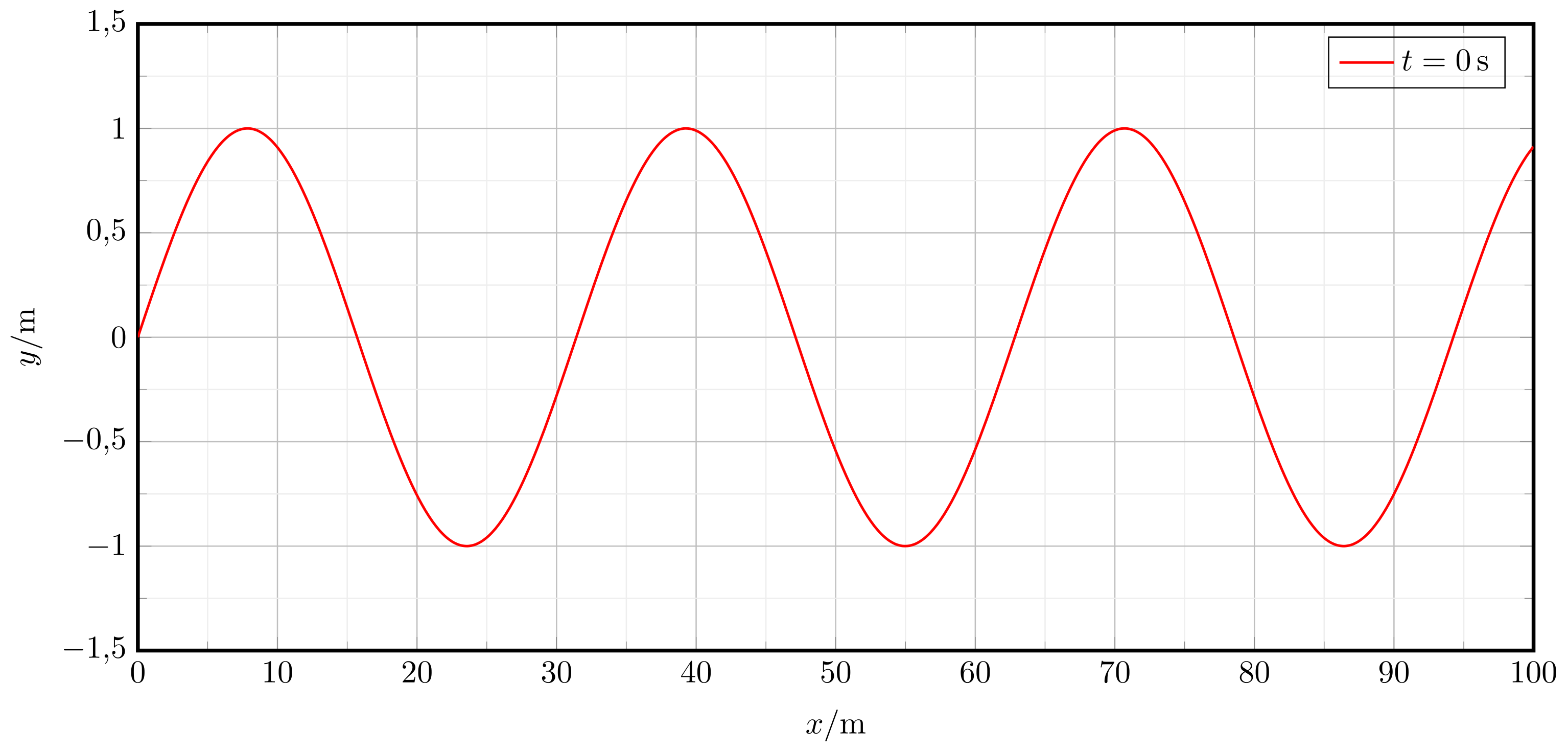
Die Welle breitet sich dann im Medium aus. Anschaulich führen die Massen dann nacheinander ebenfalls sinusförmige Bewegungen aus. Die nachfolgende Skizze zeigt, untereinander angeordnet, Momentaufnahmen einer sinusförmigen Welle die sich nach rechts bewegt. Beispielhaft ist ein Massenpunkt (grün) eingezeichnet. Der Punkt bewegt sich aufgrund der Welle auf und ab, bleibt aber an seiner Position . Der maximale Abstand der Masse von der -Achse entspricht gerade der Amplitude . Die Wellenlänge , ist durch zwei Punkte gleicher Phase gegeben. Sie kann also zum Beispiel durch den Abstand zweier benachbarter Wellenberge bestimmt werden. Die Frequenz kann aus der Zeit bestimmt werden, die vergeht bis ein Massenpunkt einen kompletten Schwingungsvorgang durchlaufen hat. In der Skizze sind die für eine Welle charakteristischen Größen eingezeichnet.
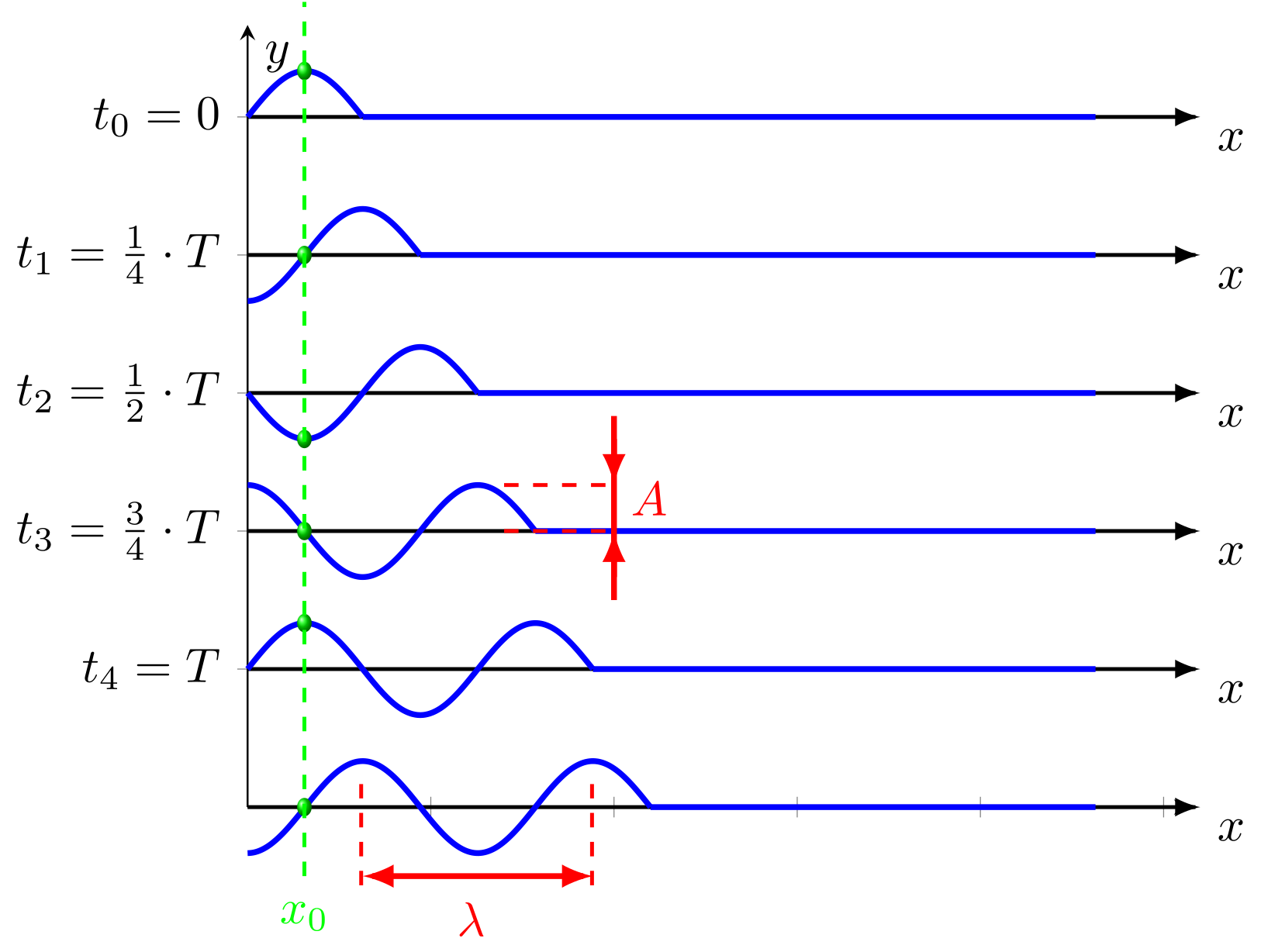
Abbildung 8.1.72: Fortschreitende Wellen durch periodische Anregung (C)
Um eine solche transversale Welle zu beschreiben, muss die von den Schwingungen bekannte Sinusfunktion erweitert werden, da mit einer Gleichung nicht nur das Verhalten eines Massenpunktes, sondern vieler benachbarter Punkte beschrieben werden soll. Die ursprüngliche, nur von der Zeit abhängige Funktion
muss um die Abhängigkeit der Bewegung von der Lage des Massenpunktes in -Richtung ergänzt werden:
Diese Gleichung beschreibt eine nach rechts laufende sinusförmige Welle. Die Auslenkung eines beliebigen Massenpunktes an einer Stelle zum Zeitpunkt kann durch einsetzen der Werte ermittelt werden .
An der obigen Skizze ist zu erkennen, dass die Ausbreitungeschwindigkeit der Welle auch über die Wellenlänge und die Periodendauer berechnet werden kann. Der grün gekennzeichnete Massenpunkt bewegt sich während einer Periode vom Maximum über den Nulldurchgang zum Minimum und wieder zurück. Gleichzeitig wandert die Welle in dieser Zeit um die Länge entlang der -Achse. Es ist also:
Da es sich bei Wellen um Schwingungen handelt, die sich in einem Medium ausbreiten, können die von den Schwingungen bekannten Größen definiert werden:
- Bei einer Welle werden die einzelnen Teilchen periodisch aus ihrer Ruhelage ausgelenkt. Die maximale Auslenkung wird als Amplitude bezeichnet und entspricht der Amplitude der erregenden Schwingung und der Welle.
- Die Wellenlänge ist bestimmt durch den Abstand zweier benachbarter Wellenberge bzw. durch den Abstand zweier benachbarter Teilchen gleicher Schwingungsphase. Sie ist weder orts- noch zeitabhängig.
- Die Periodendauer ist genau die Zeit, die vergeht, bis die erregende Schwingung einmal durchlaufen ist.
- Die Frequenz ist der Kehrwert der Periodendauer . Zwischen Winkelgeschwindigkeit und Frequenz gilt:
- Die Welle bewegt sich im Medium mit der Geschwindigkeit fort. Dabei gilt:
Aufgabe 8.1.7
Berechnen Sie die Wellenlänge folgender Wellen:
UKW mit einer Frequenz von und von Mikrowellen mit einer Frequenz von .
Überlegen Sie zuerst, um was für Wellen es sich handelt und mit welcher Geschwindigkeit sie sich in Luft ausbreiten.


Berechnen Sie die Wellenlänge folgender Wellen:
UKW mit einer Frequenz von und von Mikrowellen mit einer Frequenz von .
Überlegen Sie zuerst, um was für Wellen es sich handelt und mit welcher Geschwindigkeit sie sich in Luft ausbreiten.
Aufgabe 8.1.8
Eine sinusförmige Wasserwelle breitet sich in positiver -Richtung aus. Sie startet an der Stelle Die Frequenz beträgt und die Wellenlänge liegt bei . Nach welcher Zeit hat die Welle die Stelle erreicht?

Eine sinusförmige Wasserwelle breitet sich in positiver -Richtung aus. Sie startet an der Stelle Die Frequenz beträgt und die Wellenlänge liegt bei . Nach welcher Zeit hat die Welle die Stelle erreicht?
Aufgabe 8.1.9
Eine sinusförmige, transversale Welle breitet sich in positiver -Richtung aus. Zum Zeitpunkt startet sie an der Stelle in positiver -Richtung (). Ihre Geschwindigkeit beträgt . Die maximale Amplitude beträgt bei einer Schwingungsdauer von .
Berechnen Sie die Wellenlänge .

Nach welcher Zeit erreicht die Welle den Punkt ?

Eine sinusförmige, transversale Welle breitet sich in positiver -Richtung aus. Zum Zeitpunkt startet sie an der Stelle in positiver -Richtung (). Ihre Geschwindigkeit beträgt . Die maximale Amplitude beträgt bei einer Schwingungsdauer von .
Berechnen Sie die Wellenlänge .
Nach welcher Zeit erreicht die Welle den Punkt ?
Eindimensionale Wellenbewegung (*)
Video 2: Wellenlänge und Periodendauer (C)
.
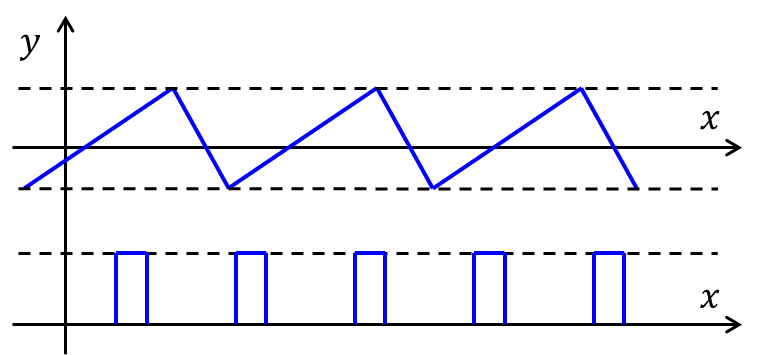
Bei einer Welle möchte man wissen, welche Form die Welle über einem bestimmten Gebiet hat (grau markierter Bereich in der Grafik unten). Man sucht eine Funktion, die die Auslenkung an einzelnen Positionen (-Koordinate) beschreibt. Da die Auslenkungen sich aber an allen Positionen in dem Gebiet auch über der Zeit verändern, muss die Zeit in dieser so genannten Wellenfunktion ebenfalls eine Variable sein.
Die durchgezogene schwarze Linie in der Grafik stellt z.B. die Auslenkung eines Seils, in dem sich gerade eine Welle fortbewegt, zum Zeitpunkt dar. Zu einem etwas späteren Zeitpunkt hat sich die Auslenkung des Seils etwas verändert und es sieht so aus, als ob die schwarze Linie um ein kleines Stück nach rechts verschoben wurde. Um eine Wellenfunktion zu definieren, braucht man also eine beliebige Kurve , die je nach Ausbreitungsrichtung der Welle in Abhängigkeit der Zeit nach links oder rechts verschoben wird. Eine Verschiebung erfolgt mathematisch gesehen dadurch, dass man zur Ortskoordinate einen bestimmten Wert addiert oder subtrahiert, der von der Zeit abhängt. Der Faktor entspricht dabei der Ausbreitungsgeschwindigkeit.
Periodische und harmonische Wellen (+)

Abbildung 8.1.73: Wellenfunktion zu verschiedenen Zeitpunkten (C)
Die durchgezogene schwarze Linie in der Grafik stellt z.B. die Auslenkung eines Seils, in dem sich gerade eine Welle fortbewegt, zum Zeitpunkt dar. Zu einem etwas späteren Zeitpunkt hat sich die Auslenkung des Seils etwas verändert und es sieht so aus, als ob die schwarze Linie um ein kleines Stück nach rechts verschoben wurde. Um eine Wellenfunktion zu definieren, braucht man also eine beliebige Kurve , die je nach Ausbreitungsrichtung der Welle in Abhängigkeit der Zeit nach links oder rechts verschoben wird. Eine Verschiebung erfolgt mathematisch gesehen dadurch, dass man zur Ortskoordinate einen bestimmten Wert addiert oder subtrahiert, der von der Zeit abhängt. Der Faktor entspricht dabei der Ausbreitungsgeschwindigkeit.
Die allgemeinste Form einer Wellenfunktion
| mit | Auslenkung der Partikel im Ausbreitungsmedium | |
| Position im Ausbreitungsgebiet | ||
| Zeit | ||
| Ausbreitungsgeschwindigkeit |
Beispiel
8.1.10
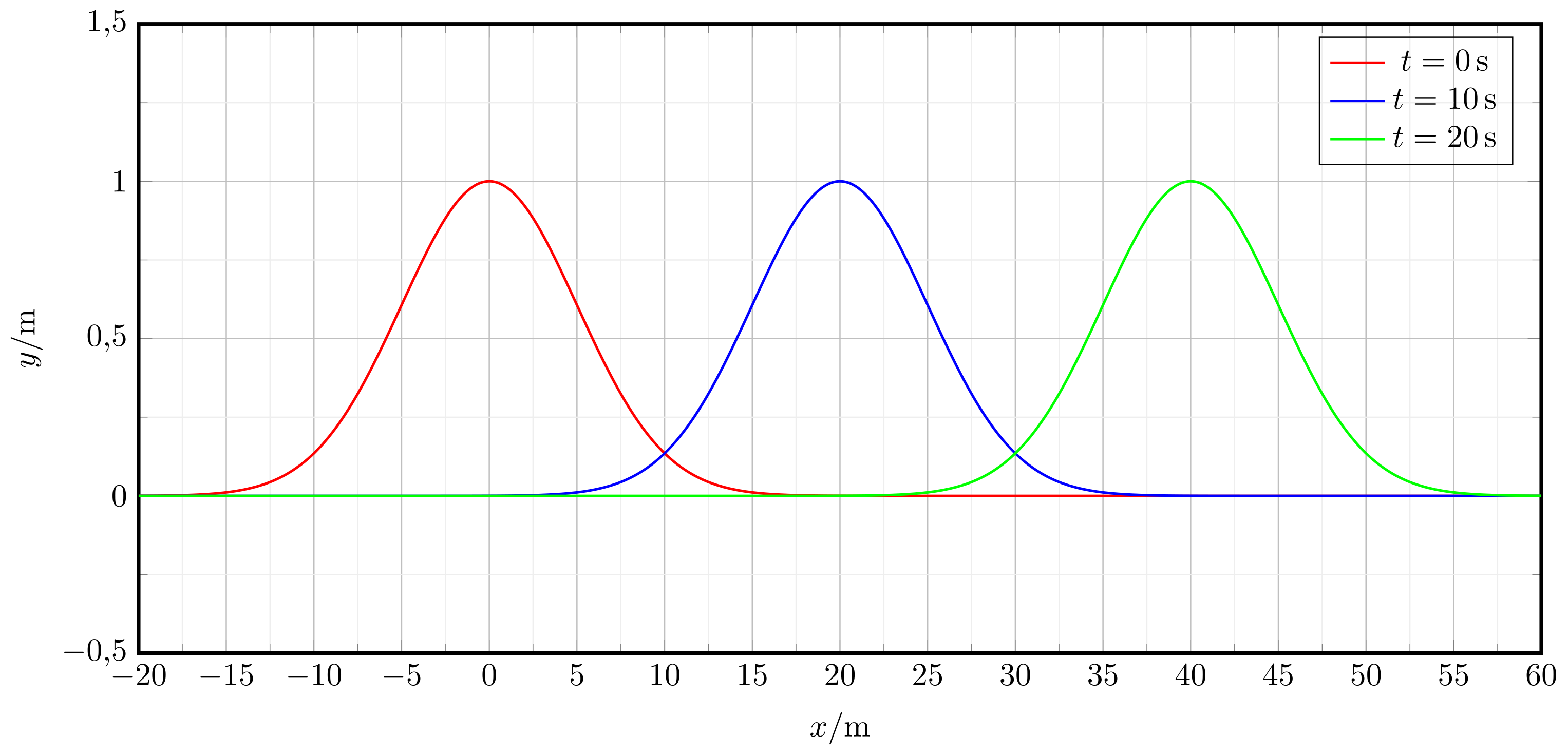
Der Wellenberg einer Seilwelle kann z.B. mithilfe einer Exponentialfunktion (Glockenfunktion) dargestellt werden:
mit:
Nachfolgend: Diagramm für .
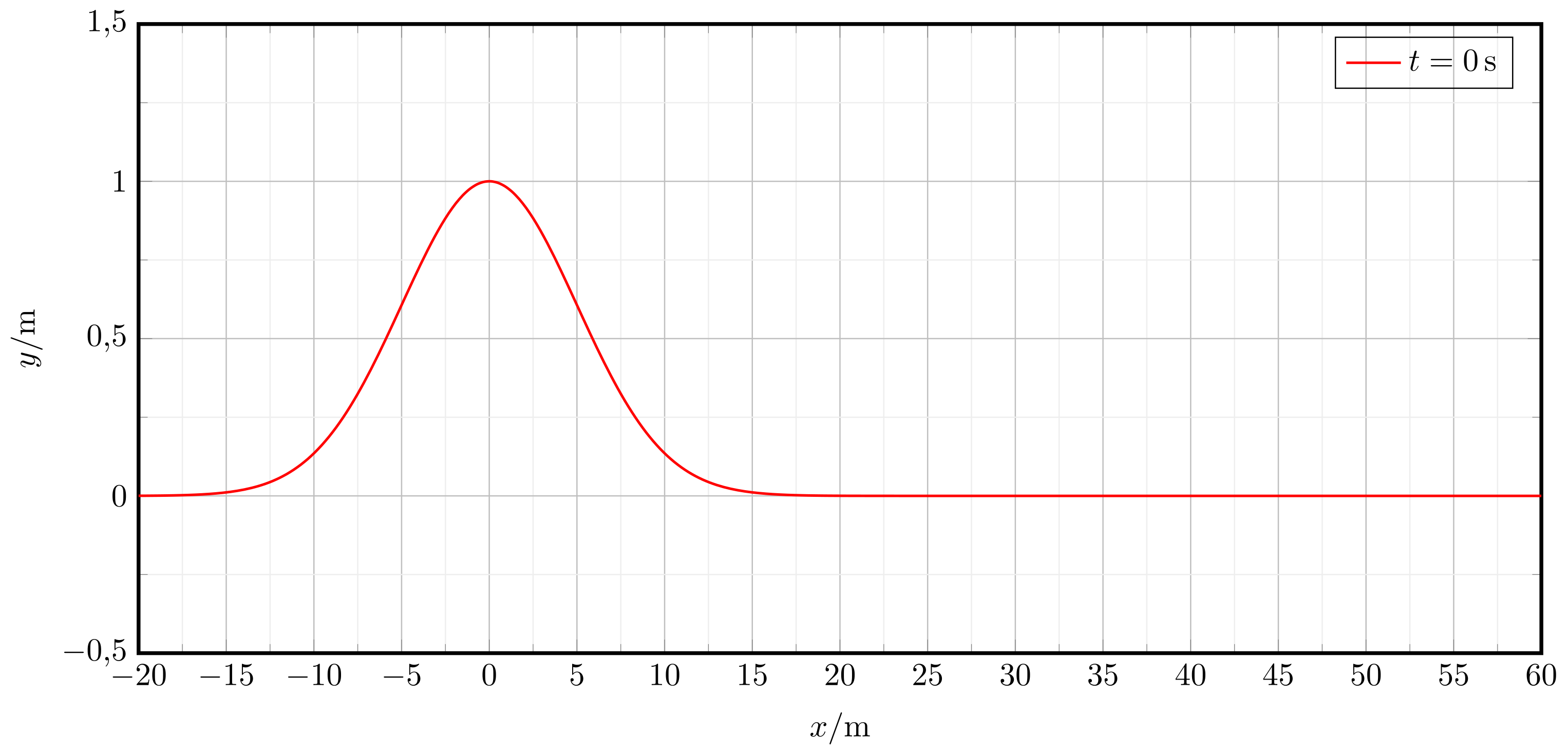
Der Wellenberg einer Seilwelle kann z.B. mithilfe einer Exponentialfunktion (Glockenfunktion) dargestellt werden:
mit:
Nachfolgend: Diagramm für .

Abbildung 8.1.74: Wellenberg einer Seilwelle für . (C)
| a) | In welche Richtung breitet sich die Welle aus? |
| b) | An welcher absoluten Position befindet sich der Wellenberg nach ? |
Periodische und harmonische Wellen (+)
Beispiel
8.1.11
Gegeben sei eine rechtslaufende Welle:
Gegeben sei eine rechtslaufende Welle:
| a) | Welche Wellenlänge besitzt die Welle? |
| b) | Bestimmen Sie die Phasengeschwindigkeit. |