4.1.10 Kräftebehandlung in der Technischen Mechanik: Freikörperbild
An dieser Stelle wird beispielhaft anhand der bereits bekannten Anordnung der schiefen Ebene die Sichtweise bzw. die Herangehensweise der Technischen Mechanik kurz erläutert.
Allgemeine Prinzipien
Alle Kräfte zwischen zwei Körpern unterliegen dem Reaktionsprinzip, d.h. zu einer gegebenen Kraft (Körper wirkt auf Körper ) gehört immer eine entsprechende Gegenkraft (Körper wirkt auf Körper ), die der ersten vektoriell entgegengesetzt gleich ist: . Dies ist die Aussage des dritten Newtonschen Axioms, siehe Abschnitt 4.1.8.
Aufgrund dessen kann ein beliebiges Teilsystem eines gesamten Gebildes vom Rest isoliert betrachtet werden, indem man die an den Grenzflächen wirkenden Kräfte innerhalb des Gebildes in Kräfte von außen nach innen und Kräfte von innen nach außen zerlegt. Auf das isolierte Teilsystem wirken dann äußere Kräfte, einerseits in Form von sogenannten Reaktionskräften an den Grenzflächen des Teilsystems zum Gesamtsystem und andererseits sogenannte eingeprägte Kräfte, die von außen auf das Gesamtsystem wirken, wie spezielle Lasten oder die Gravitationskraft. Die Abtrennung eines Teilsystems auf der Basis von Kräften bezeichnet man als Freimachen oder Freischneiden und führt auf das sogenannte Freikörperbild.
Beim Freimachen werden die nachfolgend aufgeführten Schritte durchgeführt. Dabei ist zu beachten, dass Kräfte im Allgemeinen gebundene Vektoren sind, die man entlang ihrer Wirklinie verschieben kann. Es werden nur äußere Kräfte berücksichtigt.
- Das Teilsystem wird isoliert ohne angrenzende Systemteile gezeichnet.
-
Für alle (äußeren) Kräfte werden (soweit möglich) die Angriffspunkte und die Wirklinien festgelegt.
-
Dabei ist auch der jeweilige Richtungssinn der Kraft in Bezug auf das Teilsystem festzulegen.
- Die Summe aller Kräfte verschwindet im statischen Fall. Dieses Kräftegleichgewicht gilt dann für jede Kraftkomponente in Bezug auf ein kartesisches Koordinatensystem:
bzw. komponentenweise für zwei Dimensionen:
-
Die Summe aller Drehmomente (siehe Abschnitte 4.1.2 und 4.5.2) bezüglich eines beliebigen Nullpunkts verschwindet. Dies ist insbesondere dann bereits implizit erfüllt, wenn sich die Wirklinien aller Kräfte in einem Punkt schneiden. Im Fall dreier nichtverschwindender Kräfte ist letzteres auch notwendig.
Anwendung auf die schiefe Ebene
Waagerechte Ebene:
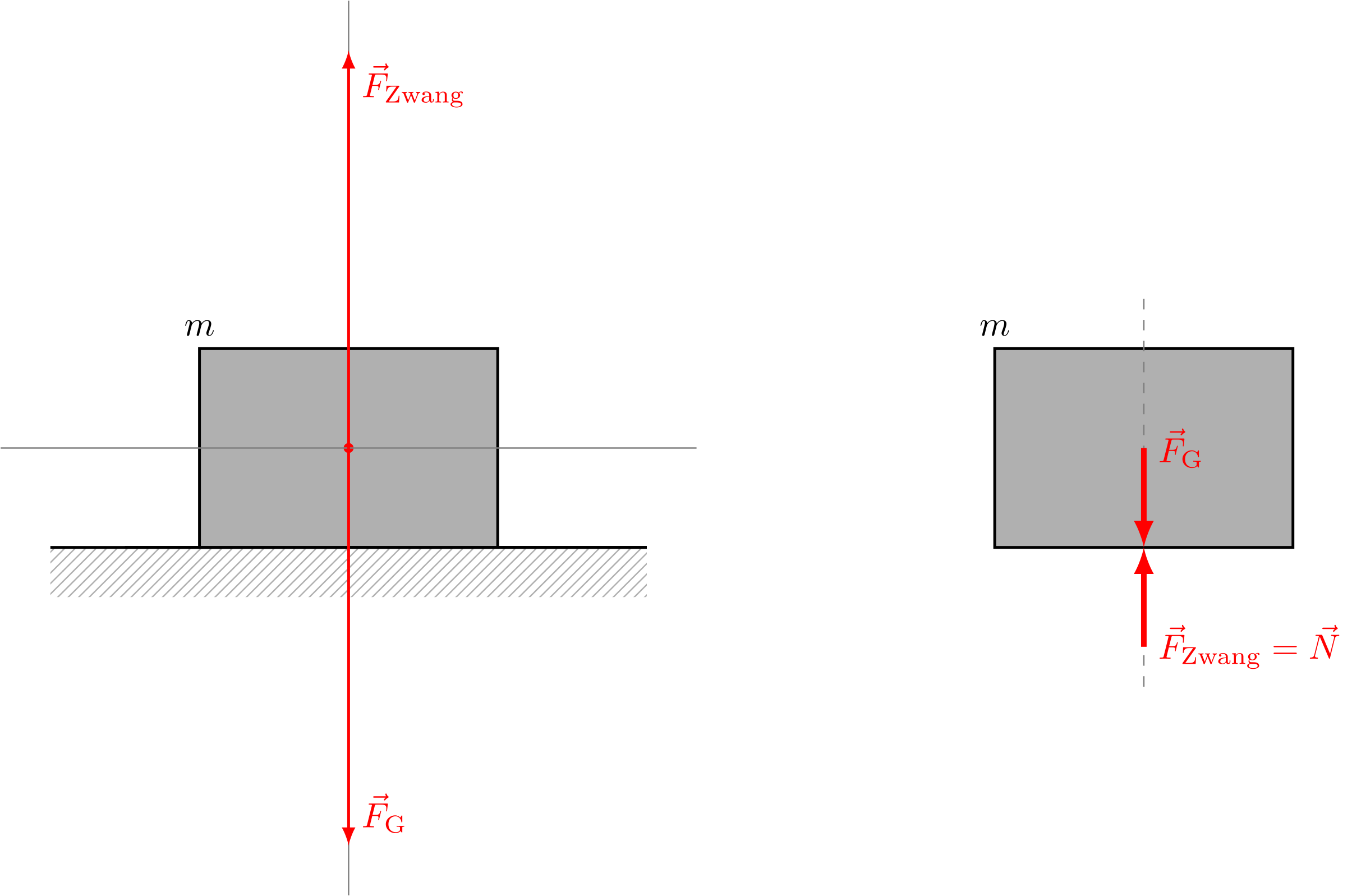
Abbildung 4.1.509: Waagerechte Ebene (C)
Schiefe Ebene mit großer Reibung:
Im nächsten Fall sei die Ebene um einen Winkel gegenüber der Waagerechten geneigt, siehe Skizze, wobei die Reibung – siehe auch Abschnitt 4.1.4 – so groß sei, dass der Körper nicht rutscht.
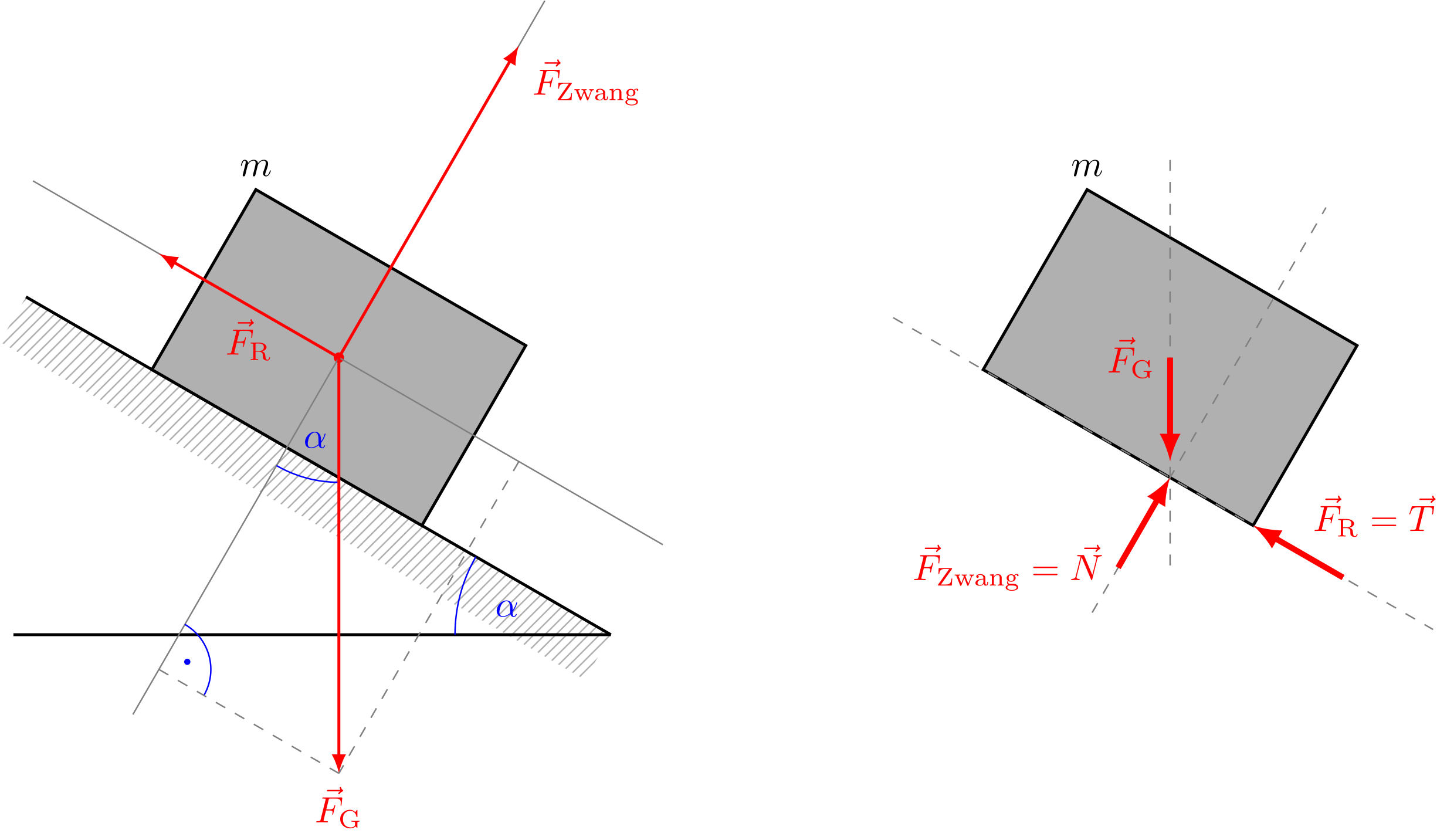
Abbildung 4.1.510: Schiefe Ebene mit großer Reibung (C)
Schiefe Ebene ohne Reibung:
Schließlich wird der Fall der reibungsfreien schiefen Ebene betrachtet; die Geometrie entspricht dabei der des vorhergehenden Falles der Ebene mit großer Reibung.
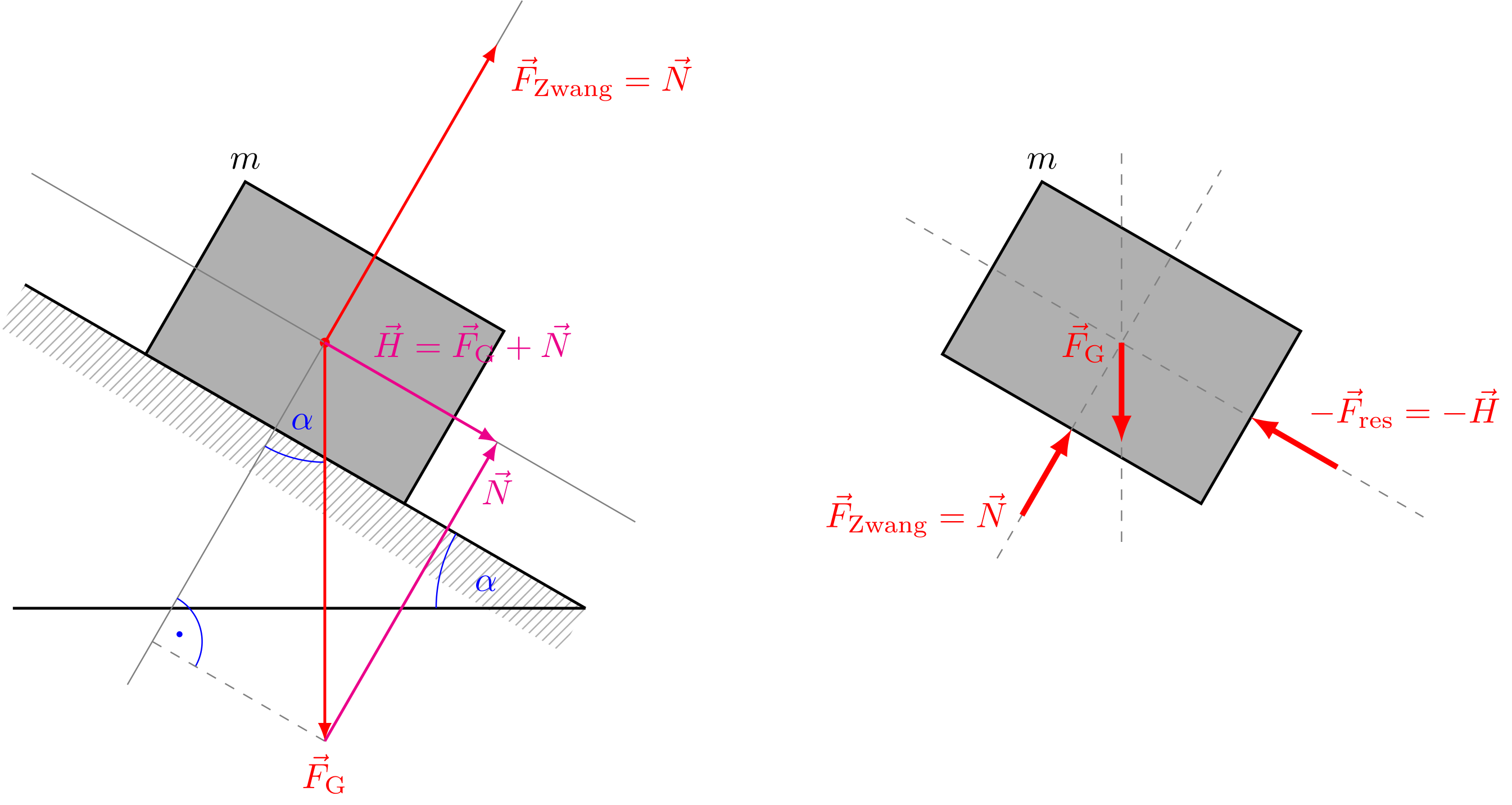
Abbildung 4.1.511: Schiefe Ebene ohne Reibung (C)

