4.2.2 Geradlinige Bewegungen
Geradlinige Bewegungen wurden bereits im Basiswissen Abschnitt 4.2.1 vorgestellt. Hier betrachten wir einige wichtige Spezialfälle.
Basiswissen – freier Fall
Beim freien Fall handelt es sich um eine gleichmäßig beschleunigte Bewegung. Dabei fällt ein Körper aus der Ruhe heraus und wird immer schneller. Hervorgerufen wird die Beschleunigung durch die Erdanziehung. Der Luftwiderstand wird vernachlässigt. Prinzipiell sind die Formeln, mit denen eine solche Bewegung beschrieben werden kann, identisch mit den schon aus dem letzten Abschnitt bekannten Gleichungen. Allerdings wird für den zurückgelegten Weg, also die Fallhöhe, ein verwendet. Als Beschleunigung wird für die Erdbeschleunigung eingesetzt.
In der Abbildung sind zwei Möglichkeiten skizziert, wie ein solches Problem betrachtet werden kann. Beide Male durchfällt ein Ball eine Strecke der Länge und trifft auf dem Boden auf. Im linken Bild ist der Nullpunkt der Bewegung auf den Start gelegt. Mit der daneben stehenden Formel kann dann der durchfallene Weg berechnet werden. Es ist die Gleichung für eine gleichmäßig beschleunigte Bewegung aus der Ruhe heraus. Im rechten Bild liegt der Nullpunkt auf dem Boden und der Ball wird in der Höhe losgelassen. Mit dieser Formel kann nun berechnet werden, in welcher Höhe der Ball sich während seines Fluges gerade befindet.
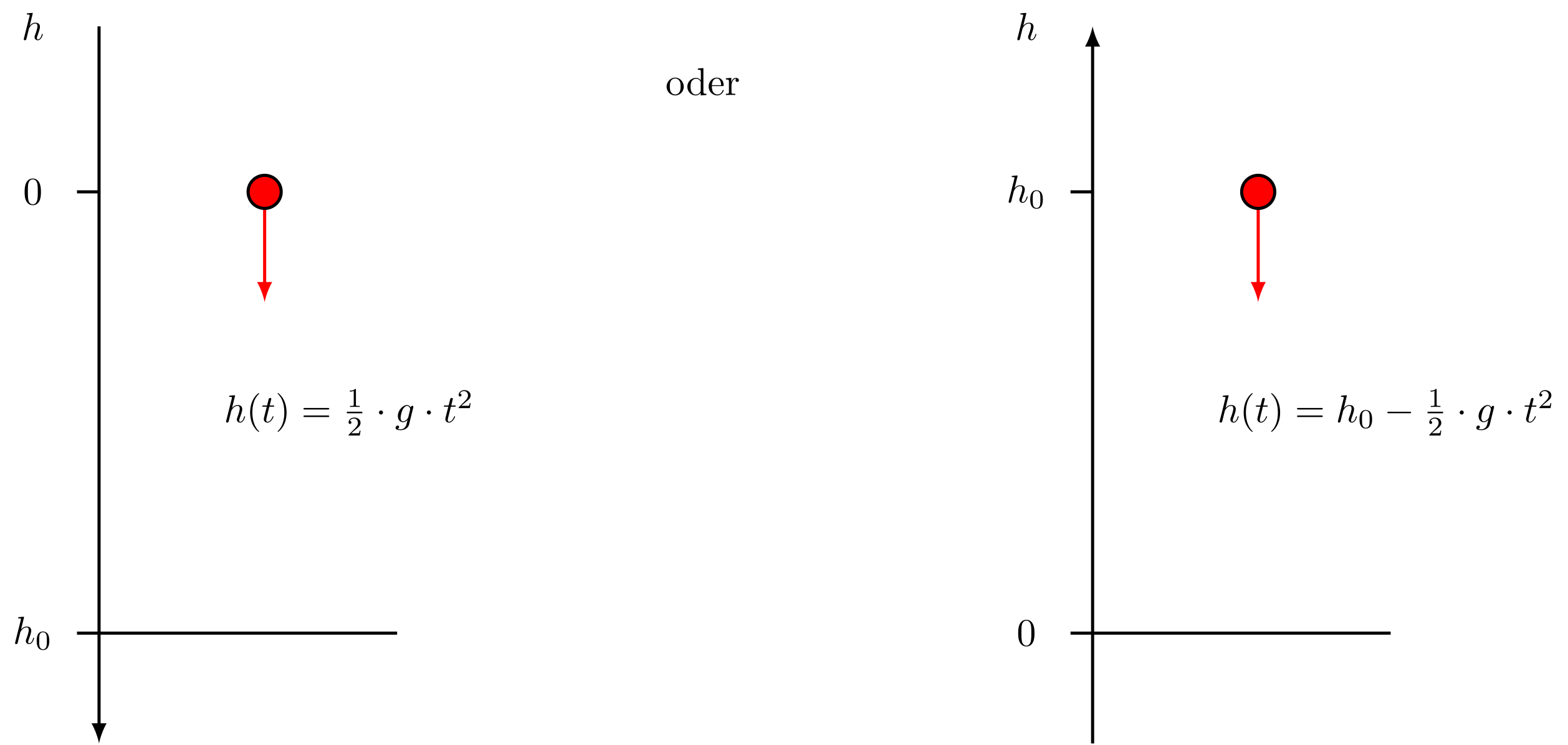
Abbildung 4.2.77: Betrachtungsweisen für freien Fall (C)
Die Gleichung zur Beschreibung der Fallstrecke, d.h. des in der Zeit durchfallenen Wegs, lautet also
oder, falls man die momentane Höhe des Körpers über dem Boden sucht,
Die erreichte Geschwindigkeit ergibt sich in beiden Fällen zu:
oder, falls man die momentane Höhe des Körpers über dem Boden sucht,
Die erreichte Geschwindigkeit ergibt sich in beiden Fällen zu:
Beispiel
4.2.23
Ein Apfel wird von der hohen Kochertalbrücke fallen gelassen. Wie lange dauert sein Fall und welche Geschwindigkeit hat er beim Erreichen des Bodens?
Die Fallzeit kann durch Umstellen aus der ersten Gleichung ermittelt werden,
Da sie nicht sinnvoll ist, scheidet die negative Lösung hier aus. Mit der berechneten Zeit ergibt sich die Geschwindigkeit nun zu:
Ein Apfel wird von der hohen Kochertalbrücke fallen gelassen. Wie lange dauert sein Fall und welche Geschwindigkeit hat er beim Erreichen des Bodens?
Die Fallzeit kann durch Umstellen aus der ersten Gleichung ermittelt werden,
Da sie nicht sinnvoll ist, scheidet die negative Lösung hier aus. Mit der berechneten Zeit ergibt sich die Geschwindigkeit nun zu:
Beispiel
4.2.24
Ein Fallschirmspringer springt in Höhe aus einem Flugzeug ab. Er stürzt im freien Fall der Erde zu und zieht dann die Reißleine des Fallschirms. In welcher Höhe befindet er sich zu diesem Zeitpunkt?
Hier verwendet man am besten die zweite Formel, da der Abstand von der Erde gesucht ist. Für die Starthöhe gilt hier und für die Flugzeit . Damit können wir ausrechnen, in welcher Höhe über dem Boden der Fallschirm geöffnet wird:
Als zugehörige Endgeschwindigkeit erhält man in diesem Fall
In der Realität wirkt bei einem Fallschirmsprung natürlich der Luftwiderstand der Bewegung entgegen, dadurch dauert der Flug länger und die Geschwindigkeit erreicht, abhängig von der Sprunghaltung, einen maximalen Wert von nur etwa . Der Fallschirm wird üblicherweise in einer Höhe zwischen und über dem Boden geöffnet. Diese Höhe erreicht man bei einem Sprung aus nach etwa –.
Ein Fallschirmspringer springt in Höhe aus einem Flugzeug ab. Er stürzt im freien Fall der Erde zu und zieht dann die Reißleine des Fallschirms. In welcher Höhe befindet er sich zu diesem Zeitpunkt?
Hier verwendet man am besten die zweite Formel, da der Abstand von der Erde gesucht ist. Für die Starthöhe gilt hier und für die Flugzeit . Damit können wir ausrechnen, in welcher Höhe über dem Boden der Fallschirm geöffnet wird:
Als zugehörige Endgeschwindigkeit erhält man in diesem Fall
In der Realität wirkt bei einem Fallschirmsprung natürlich der Luftwiderstand der Bewegung entgegen, dadurch dauert der Flug länger und die Geschwindigkeit erreicht, abhängig von der Sprunghaltung, einen maximalen Wert von nur etwa . Der Fallschirm wird üblicherweise in einer Höhe zwischen und über dem Boden geöffnet. Diese Höhe erreicht man bei einem Sprung aus nach etwa –.
Basiswissen – senkrechter Wurf
Beim senkrechten Wurf wird ein Körper nach unten oder oben geworfen. Auch hier soll die Luftreibung bei den folgenden Betrachtungen vernachlässigt werden. In der Abbildung ist skizziert, in welche Richtung sich der Körper mit der Anfangsgeschwindigkeit bewegt und in welche Richtung die Erdbeschleunigung zeigt.
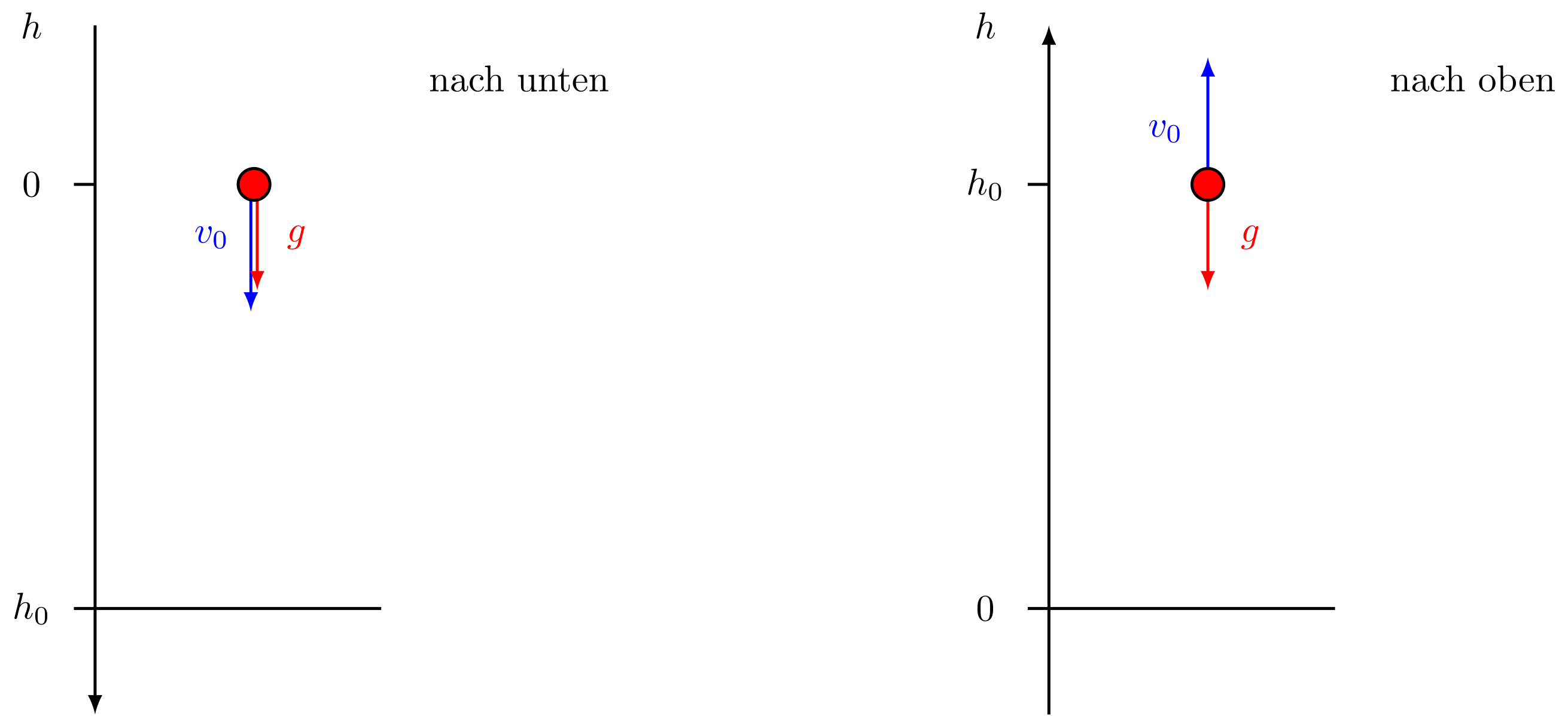
Abbildung 4.2.78: Senkrechter Wurf (C)
Fall 1: Der Körper wird nach unten geworfen (im Bild links).
Beim Abwurf startet der Körper mit der konstanten Geschwindigkeit nach unten, und zugleich wird er mit der Erdbeschleunigung gleichmäßig in dieselbe Richtung beschleunigt. Seine Geschwindigkeit wird also mit fortlaufender Zeit immer größer. Diese Bewegung kann mit den schon bekannten Formeln beschrieben werden.
Der durchfallene Weg und die Geschwindigkeit ergeben sich zu:
und
und
Beispiel
4.2.25
Ein Ball wird in einer Höhe von vom Turm des Ulmer Münsters nach unten geworfen. Nach kommt er auf dem Boden an. Mit welcher Geschwindigkeit ist der Ball nach unten geworfen worden und welche Endgeschwindigkeit erreicht er?
Zur Bestimmung der Anfangsgeschwindigkeit wird die Gleichung für die Höhe umgeformt:
Die Endgeschwindigkeit beim Aufprall auf die Erde ergibt sich dann zu
Ein Ball wird in einer Höhe von vom Turm des Ulmer Münsters nach unten geworfen. Nach kommt er auf dem Boden an. Mit welcher Geschwindigkeit ist der Ball nach unten geworfen worden und welche Endgeschwindigkeit erreicht er?
Zur Bestimmung der Anfangsgeschwindigkeit wird die Gleichung für die Höhe umgeformt:
Die Endgeschwindigkeit beim Aufprall auf die Erde ergibt sich dann zu
Fall 2: Der Körper wird nach oben geworfen (im Bild rechts)
Auch hier startet der Körper mit einer konstanten Geschwindigkeit . Allerdings bewegt er sich jetzt zu Beginn nach oben. Dieser gleichförmigen Bewegung wirkt die Erdanziehung entgegen, d.h. der Körper wird mit abgebremst. Im höchsten Punkt seiner Bahn ist die Geschwindigkeit des Körpers kurzzeitig null. Im Anschluss daran fällt der Körper wieder im freien Fall nach unten. Die Zeit die vergeht, bis der Umkehrpunkt erreicht ist, kann aus der Gleichung für die Geschwindigkeit berechnet werden.
Im Scheitelpunkt gilt für die Geschwindigkeit
Aus
kann nun mit dieser Flugzeit die Steighöhe bestimmt werden:
Aus
kann nun mit dieser Flugzeit die Steighöhe bestimmt werden:
Beispiel
4.2.26
Eine Kugel wird vom Boden aus senkrecht nach oben geschossen. Ihre Anfangsgeschwindigkeit beträgt . Wie hoch steigt die Kugel und wie lange dauert es, bis sie den Boden erreicht?
Die Steighöhe kann mit Hilfe der obigen Beziehung ermittelt werden,
Über die Zeit, die die Kugel braucht, um den Umkehrpunkt zu erreichen, kann die gesamte Flugzeit ermittelt werden,
Der Körper braucht zum Fallen genauso viel Zeit, wie er zum Steigen gebraucht hat. Die gesamte Flugzeit beträgt also .
Eine Kugel wird vom Boden aus senkrecht nach oben geschossen. Ihre Anfangsgeschwindigkeit beträgt . Wie hoch steigt die Kugel und wie lange dauert es, bis sie den Boden erreicht?
Die Steighöhe kann mit Hilfe der obigen Beziehung ermittelt werden,
Über die Zeit, die die Kugel braucht, um den Umkehrpunkt zu erreichen, kann die gesamte Flugzeit ermittelt werden,
Der Körper braucht zum Fallen genauso viel Zeit, wie er zum Steigen gebraucht hat. Die gesamte Flugzeit beträgt also .
Wenn in den folgenden Aufgabentexten nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie
Aufgabe 4.2.27
Zwei Birnen hängen in einem Abstand von übereinander an einem Baum. Zufälligerweise fallen beide zum gleichen Zeitpunkt vom Baum. Wie verändert sich der Abstand zwischen den beiden Birnen während des Falls?
Zwei Birnen hängen in einem Abstand von übereinander an einem Baum. Zufälligerweise fallen beide zum gleichen Zeitpunkt vom Baum. Wie verändert sich der Abstand zwischen den beiden Birnen während des Falls?
| Gar nicht. Der Abstand zwischen beiden bleibt gleich. | |
| Der Abstand wird größer. | |
| Der Abstand wird kleiner. | |
| Das kann man ohne weitere Angaben nicht sagen. |
Aufgabe 4.2.28
Welche Zeit braucht ein frei fallender Körper, um eine Geschwindigkeit von zu erreichen? Es soll angenommen werden, dass ist.

Welche Zeit braucht ein frei fallender Körper, um eine Geschwindigkeit von zu erreichen? Es soll angenommen werden, dass ist.
Aufgabe 4.2.29
Welche Strecke durchfällt ein Körper in im freien Fall unter der Annahme, dass ist?

Welche Strecke durchfällt ein Körper in im freien Fall unter der Annahme, dass ist?
Aufgabe 4.2.30
Zwei Früchte hängen übereinander an einem Baum. Die obere Frucht fällt. Zu dem Zeitpunkt, an dem sie an der unteren vorbeifällt, fällt diese ebenfalls. Welche Frucht trifft zuerst auf dem Boden auf?
Zwei Früchte hängen übereinander an einem Baum. Die obere Frucht fällt. Zu dem Zeitpunkt, an dem sie an der unteren vorbeifällt, fällt diese ebenfalls. Welche Frucht trifft zuerst auf dem Boden auf?
| Die Untere. | |
| Ohne genauere Angaben kann die Frage nicht beantwortet werden. | |
| Die Obere. | |
| Beide gleichzeitig. |
Aufgabe 4.2.31
Der goldene Ball der Prinzessin fällt in einen tiefen Brunnen. Nach welcher Zeit hört sie, dass der Ball die Wasseroberfläche erreicht hat?
Die Schallgeschwindigkeit beträgt und für die Erdbeschleunigung soll angenommen werden.
Der goldene Ball der Prinzessin fällt in einen tiefen Brunnen. Nach welcher Zeit hört sie, dass der Ball die Wasseroberfläche erreicht hat?
Die Schallgeschwindigkeit beträgt und für die Erdbeschleunigung soll angenommen werden.
| nach | |
| nach | |
| nach | |
| nach | |
| nach |
Aufgabe 4.2.32
Ein Ball wird mit einer Startgeschwindigkeit von senkrecht nach oben geworfen. Wie hoch steigt der Ball?
Nehmen Sie für die Erdbeschleunigung an.

Ein Ball wird mit einer Startgeschwindigkeit von senkrecht nach oben geworfen. Wie hoch steigt der Ball?
Nehmen Sie für die Erdbeschleunigung an.
Aufgabe 4.2.33
Ein Ball wird mit nach oben geschossen. Wie lange dauert es, bis er seinen Umkehrpunkt erreicht?
Nehmen Sie für die Erdbeschleunigung an.

Ein Ball wird mit nach oben geschossen. Wie lange dauert es, bis er seinen Umkehrpunkt erreicht?
Nehmen Sie für die Erdbeschleunigung an.
Aufgabe 4.2.34
Ein Körper wird mit einer Geschwindigkeit von senkrecht nach oben geschossen. Welche Höhe hat er nach einer Flugzeit von ?
Nehmen Sie für die Erdbeschleunigung an.

Ein Körper wird mit einer Geschwindigkeit von senkrecht nach oben geschossen. Welche Höhe hat er nach einer Flugzeit von ?
Nehmen Sie für die Erdbeschleunigung an.
Aufgabe 4.2.35
Ein Ball wird mit nach oben geschossen. Wie lange dauert es, bis seine Geschwindigkeit beträgt?
Nehmen Sie für die Erdbeschleunigung an.

Ein Ball wird mit nach oben geschossen. Wie lange dauert es, bis seine Geschwindigkeit beträgt?
Nehmen Sie für die Erdbeschleunigung an.
Aufgabe 4.2.36
Sie schießen eine Kugel mit einer Geschwindigkeit von nach oben. Wie lange dauert es, bis die Kugel die Höhe passiert und welche Geschwindigkeit hat die Kugel zu diesem Zeitpunkt?
Nehmen Sie für die Erdbeschleunigung an.




Sie schießen eine Kugel mit einer Geschwindigkeit von nach oben. Wie lange dauert es, bis die Kugel die Höhe passiert und welche Geschwindigkeit hat die Kugel zu diesem Zeitpunkt?
Nehmen Sie für die Erdbeschleunigung an.
In diesem Abschnitt werden geradlinige Bewegungen betrachtet, also Bewegungen in eine feste Richtung.
Diese werden auch eindimensionale Bewegungen genannt. Im Folgenden werden Kenntnisse aus dem Bereich der Integralrechnung benötigt, die z.B. im
Onlinekurs Mathematik, Kapitel 8 behandelt werden.
Geradlinige und gleichförmige Bewegung (!)
Geradlinige und gleichförmige Bewegung (!)
Video 19: Geradlinige und gleichförmige Bewegung: Weg-Zeit-Gesetz der geradlinig gleichförmigen Bewegung (C)
.

Abbildung 4.2.79: Körper mit Geschwindigkeit (C)
Die geradlinig gleichförmige Bewegung ist die Bewegung in eine feste Richtung bei konstanter Geschwindigkeit. In der vorher eingeführten Definition der Geschwindigkeit als zeitliche Ableitung des Ortes setzt man eine konstante Geschwindigkeit ein,
und erhält dann die Ortsfunktion durch Integration über die Zeit ,
Hierbei ist die Integrationskonstante. Sie folgt aus der Randbedingung, dass sich der Körper zum Zeitpunkt an der Stelle befindet.
Das Ergebnis ist natürlich nicht erstaunlich. Man hätte die zurückgelegte Strecke auch direkt als das Produkt aus der Geschwindigkeit und der Zeitdauer berechnen können. Die obige zeitliche Integration dient aber als einfaches Beispiel zur Einführung. Eine entsprechende Integration über die Zeit wird auch gleich bei der beschleunigten Bewegung wieder durchgeführt.
Beispiel für mit und :
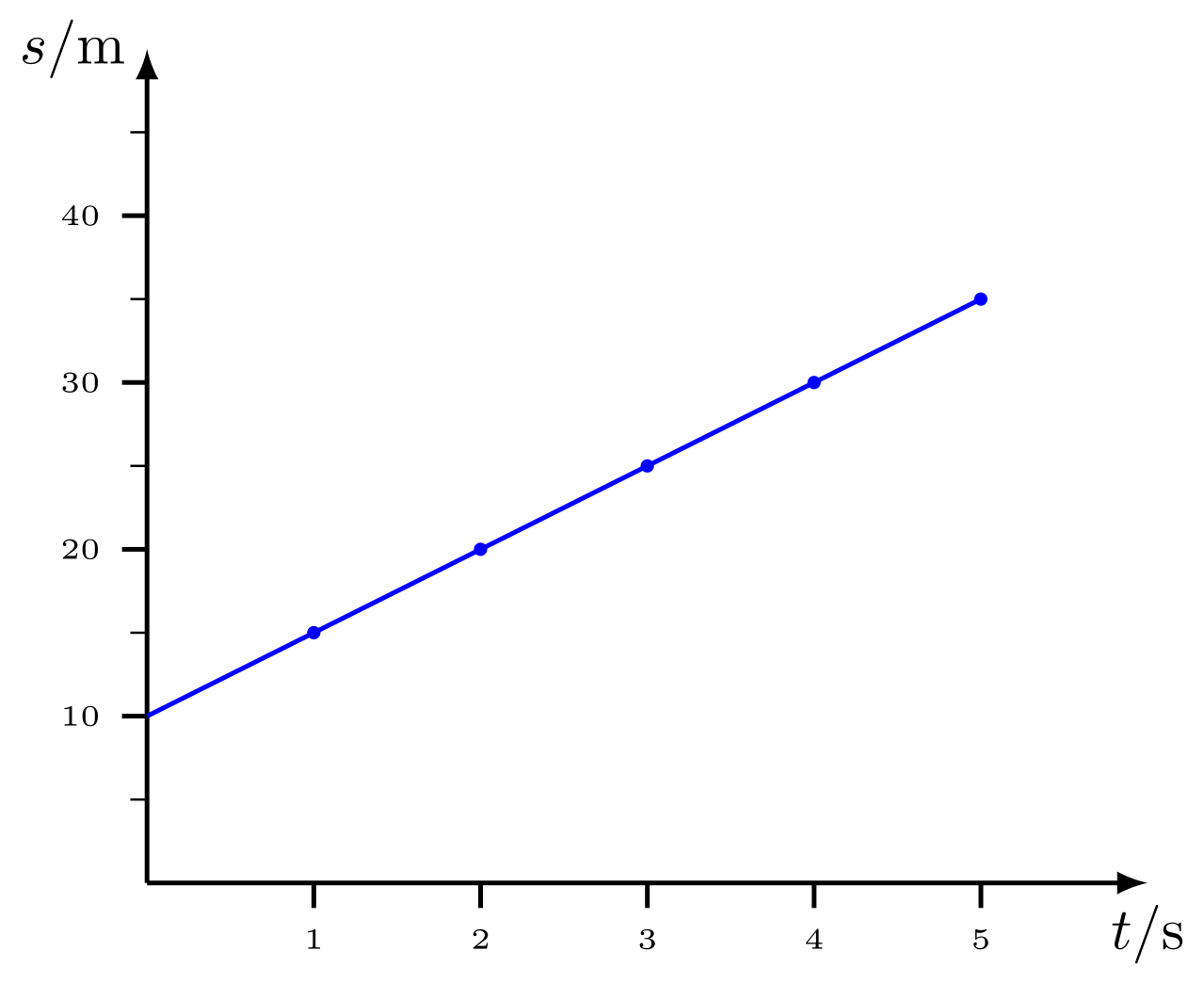
Abbildung 4.2.80: Weg-Zeit-Diagramm bei konstanter Geschwindigkeit (C)
Video 20: Geradlinige und gleichförmige Bewegung: Beispiel (C)
.
Geradlinige und gleichmäßig beschleunigte Bewegung (!)
Video 21: Geradlinige und gleichmäßig beschleunigte Bewegung: Geschwindigkeits-Zeit-Gesetz (C)
.
Bei einer beschleunigten Bewegung hängt die Geschwindigkeit von der Zeit ab.
Die Geschwindigkeitsfunktion erhält man durch die zeitliche Integration der Beschleunigungsfunktion .
Bei einer gleichförmig beschleunigten Bewegung ist konstant.
Die Integration ist wieder einfach:
Die Geschwindigkeit steigt linear mit der Zeit an. Als Integrationskonstante erhält man die Anfangsgeschwindigkeit zur Zeit .
Die Geschwindigkeit steigt linear mit der Zeit an. Als Integrationskonstante erhält man die Anfangsgeschwindigkeit zur Zeit .
Video 22: Geradlinige und gleichmäßig beschleunigte Bewegung: Weg-Zeit-Gesetz (C)
.
Die Ortsfunktion erhalten wir wieder über die zeitliche Integration der Geschwindigkeitsfunktion :
Der zurückgelegte Weg nimmt quadratisch mit der Zeit zu.
Zusammenfassend erhält man damit die folgenden funktionalen Abhängigkeiten:
Die Beziehungen für die Bewegung bei konstanter Geschwindigkeit erhält man durch Einsetzen von . Sie können also als Spezialfall aus den allgemeinen Beziehungen hergeleitet werden und brauchen deshalb nicht gesondert gemerkt zu werden.
Die Beziehungen für die Bewegung bei konstanter Geschwindigkeit erhält man durch Einsetzen von . Sie können also als Spezialfall aus den allgemeinen Beziehungen hergeleitet werden und brauchen deshalb nicht gesondert gemerkt zu werden.
Video 23: Geradlinige und gleichmäßig beschleunigte Bewegung: Grafische Darstellung (C)
.
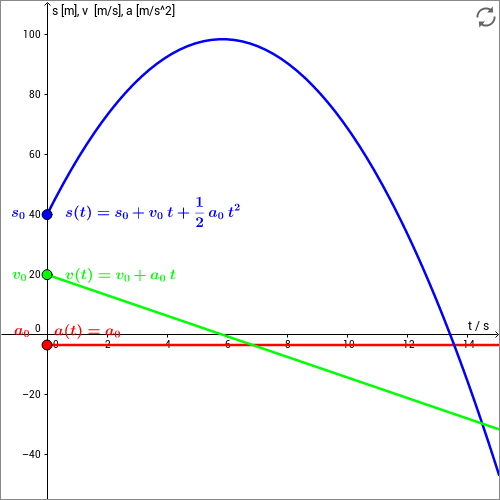
In der folgenden Skizze werden die soeben gewonnenen Bewegungsgesetze graphisch dargestellt. Durch Ziehen an den Schnittpunkten der Kurven entlang der vertikalen Achse können Sie die Anfangswerte , und variieren und damit verschiedene Bewegungen unter konstanter Beschleunigung darstellen.
Setzen Sie zunächst alle Anfangswerte auf 0.
Schieben Sie dann die Anfangsgeschwindigkeit (grüner Punkt) auf einen positiven Wert und beobachten Sie, wie sich die Ortsfunktion dabei ändert.
Schieben Sie jetzt den Startort (blauer Punkt) zunächst auf einen negativen Wert. Beobachten Sie, wie sich die Geschwindigkeitsfunktion und die Ortsfunktion ändern, wenn Sie die Beschleunigung (roter Punkt) variieren. Überlegen Sie dabei auch immer, wie sich der Körper bewegt! Wird er immer schneller oder wird er erst abgebremst und danach in die Gegenrichtung beschleunigt?
Video 24: Geradlinige und gleichmäßig beschleunigte Bewegung: Beispiel (C)
.
Video 25: Geradlinige und gleichmäßig beschleunigte Bewegung: Beispiel (C)
.
„Versteckte“ Zeitvariable
Video 26: "Versteckte Zeitvariable" (C)
.
Bei manchen Aufgaben zur geradlinigen Bewegung gehört die Zeit nicht zu den gegebenen Werten.
Man muss sie dann aus den Gleichungen eliminieren.
Hierfür löst man die Gleichung für die Geschwindigkeit nach der Zeit auf und setzt diese dann in die Gleichung für den Ort ein:
So kann man z.B. die Frage beantworten, welchen Bremsweg ein Auto mit gegebener Bremsverzögerung und Anfangsgeschwindigkeit hat.
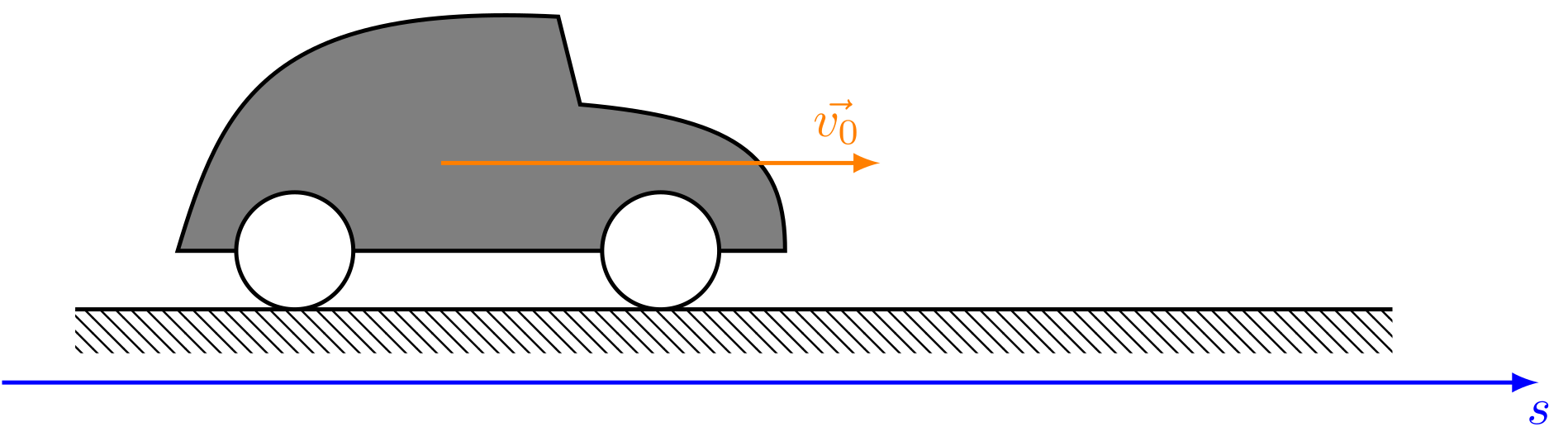
Man legt den Beginn des Bremswegs auf fest. Der Bremsweg ist die Strecke, nach der die Geschwindigkeit auf null abgesunken ist:
Da die Beschleunigung im vorliegenden Fall eine Verzögerung ist, gilt . Dies liefert ein positives Resultat für den Bremsweg . Das obige Ergebnis ist sehr bedeutend in der Verkehrssicherheit. Es besagt, dass eine Verdopplung der Geschwindigkeit zu einer Vervierfachung des Bremswegs führt. Denn der Bremsweg hängt quadratisch von der Anfangsgeschwindigkeit ab. Intuitiv mag man das zunächst nicht einsehen, da es sich ja um eine konstante (negative) Beschleunigung über den ganzen Bremsweg handelt. Nur erfolgt die konstante, lineare Abnahme der Geschwindigkeit in Bezug auf die Zeit und nicht auf den Ort.
Dies ist nochmals in der folgenden interaktiven Skizze illustriert. Es wird die Abbremsung eines Fahrzeugs mit der Anfangsgeschwindigkeit berechnet, das mit einer konstanten Beschleunigung von abgebremst wird. Aufgetragen ist die Geschwindigkeit in Abhängigkeit von der zurückgelegten Strecke. Man sieht direkt, dass dies kein linearer Verlauf ist. Bei der voreingestellten Anfangsgeschwindigkeit von () erhält man einen Bremsweg von .
Setzen Sie nun durch Ziehen am grünen Punkt die Anfangsgeschwindigkeit einmal auf und einmal auf das Doppelte, . Welches Verhältnis ergibt sich zwischen den Bremswegen?
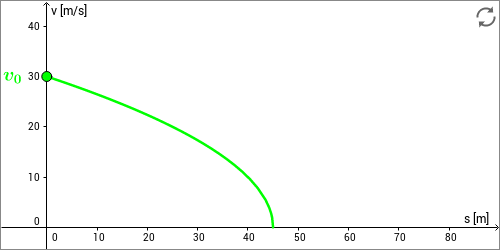 Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)
So kann man z.B. die Frage beantworten, welchen Bremsweg ein Auto mit gegebener Bremsverzögerung und Anfangsgeschwindigkeit hat.

Abbildung 4.2.82: Bremsweg eines Autos (C)
Man legt den Beginn des Bremswegs auf fest. Der Bremsweg ist die Strecke, nach der die Geschwindigkeit auf null abgesunken ist:
Da die Beschleunigung im vorliegenden Fall eine Verzögerung ist, gilt . Dies liefert ein positives Resultat für den Bremsweg . Das obige Ergebnis ist sehr bedeutend in der Verkehrssicherheit. Es besagt, dass eine Verdopplung der Geschwindigkeit zu einer Vervierfachung des Bremswegs führt. Denn der Bremsweg hängt quadratisch von der Anfangsgeschwindigkeit ab. Intuitiv mag man das zunächst nicht einsehen, da es sich ja um eine konstante (negative) Beschleunigung über den ganzen Bremsweg handelt. Nur erfolgt die konstante, lineare Abnahme der Geschwindigkeit in Bezug auf die Zeit und nicht auf den Ort.
Dies ist nochmals in der folgenden interaktiven Skizze illustriert. Es wird die Abbremsung eines Fahrzeugs mit der Anfangsgeschwindigkeit berechnet, das mit einer konstanten Beschleunigung von abgebremst wird. Aufgetragen ist die Geschwindigkeit in Abhängigkeit von der zurückgelegten Strecke. Man sieht direkt, dass dies kein linearer Verlauf ist. Bei der voreingestellten Anfangsgeschwindigkeit von () erhält man einen Bremsweg von .
Setzen Sie nun durch Ziehen am grünen Punkt die Anfangsgeschwindigkeit einmal auf und einmal auf das Doppelte, . Welches Verhältnis ergibt sich zwischen den Bremswegen?

Video 27: "Versteckte Zeitvariable": Beispiel (C)
.
Der freie Fall (!)
Video 28: Der freie Fall (C)
.
Video 29: Der freie Fall (alternative Herangehensweise) (C)
.
Der freie Fall ist ein Beispiel für die geradlinig beschleunigte Bewegung.
Dabei stellt man sich einen Körper (z.B. einen Stein) vor, der von einer erhöhten Position (z.B. von einem Turm)
frei fallen gelassen wird.
Er fällt dann mit der konstanten Beschleunigung in Richtung der Erdoberfläche.
Dabei ist die schon bekannte Erdbeschleunigung, die im Mittel beträgt.
Wenn man die Luftreibung vernachlässigt, fallen alle Körper unabhängig von ihrer Masse mit der gleichen Beschleunigung,
nämlich der Erdbeschleunigung .
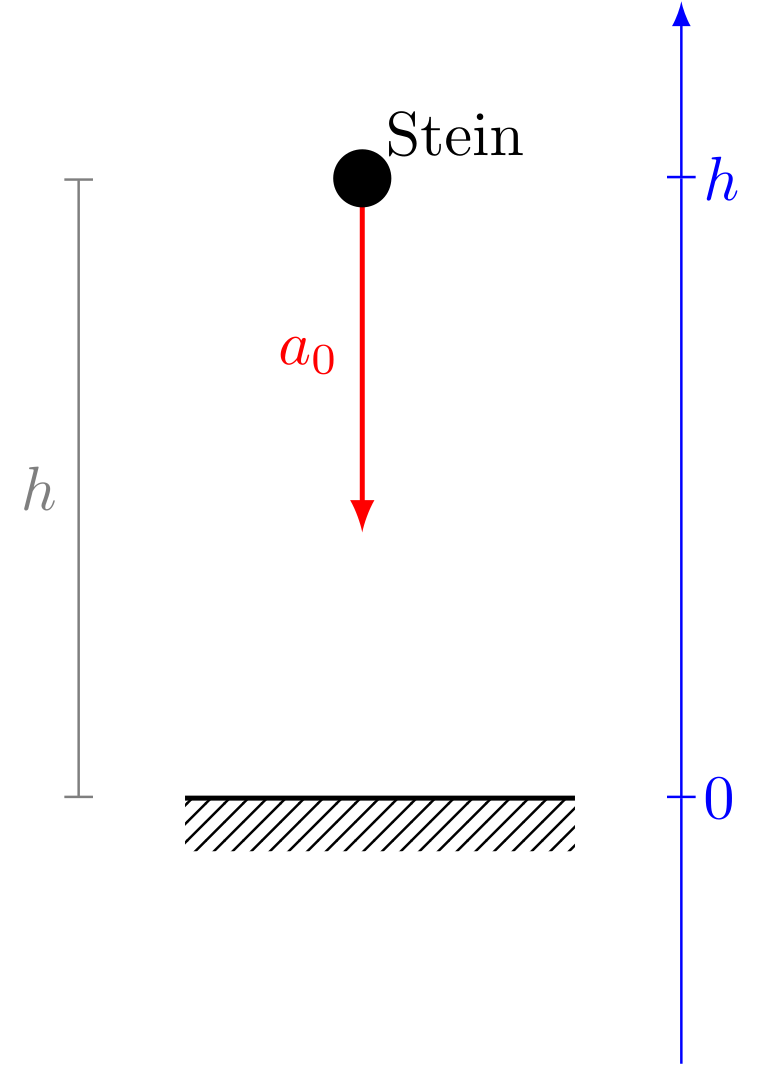
Legt man die Ortsachse der eindimensionalen Bewegung so, dass sie vertikal nach oben zeigt, und weiterhin die Erdoberfläche als ihren Nullpunkt fest, so ergeben sich die folgenden (Anfangs-)Bedingungen:

Abbildung 4.2.84: Frei fallender Stein (C)
Legt man die Ortsachse der eindimensionalen Bewegung so, dass sie vertikal nach oben zeigt, und weiterhin die Erdoberfläche als ihren Nullpunkt fest, so ergeben sich die folgenden (Anfangs-)Bedingungen:
- Der Körper wird mit nach unten beschleunigt: .
- Er startet in Ruhe: .
- Er startet bei der Höhe : .
Video 30: Der freie Fall: Falldauer und Aufschlaggeschwindigkeit (C)
.
Die Falldauer ist erreicht, wenn der Körper am Erdboden bei angekommen ist:
Als Aufschlaggeschwindigkeit am Ende des Falls ergibt sich zu
Man erhält ein negatives Ergebnis, weil der Körper mit einer Geschwindigkeit entgegen der Richtung der Ortsachse fällt.
In der folgenden Skizze ist diese Rechnung nochmals visualisiert. Am Schnittpunkt der Ortsfunktion mit der Zeitachse, also wenn gilt , kann der Zeitpunkt abgelesen werden, an dem der Körper den Erdboden erreicht. Der Wert der Geschwindigkeitsfunktion an dieser Stelle liefert dann die Aufschlaggeschwindigkeit .
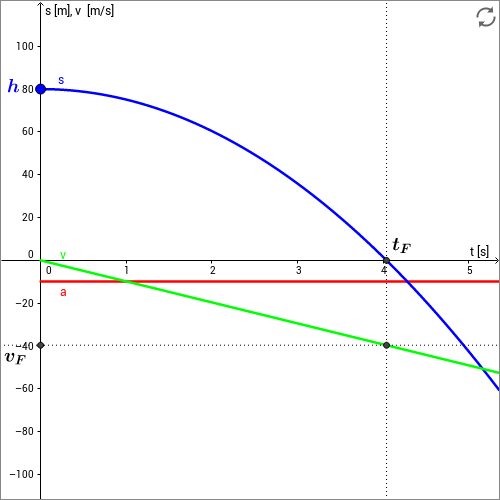
Video 31: Der freie Fall: Beispiel (C)
.
Der senkrechte Wurf (!)
Video 32: Der senkrechte Wurf: Weg-Zeit-Gesetz und Geschwindigkeits-Zeit-Gesetz (C)
.
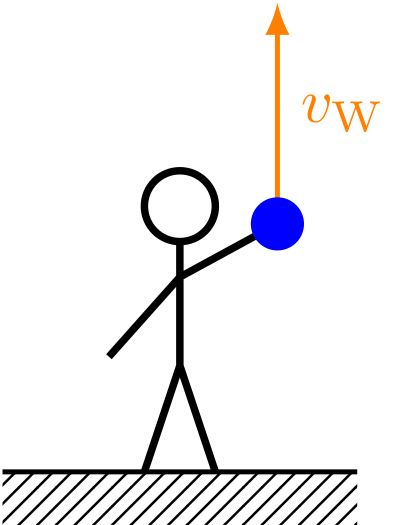
Abbildung 4.2.86: Kind wirft Ball senkrecht nach oben (C)
Beim senkrechten Wurf wird ein Körper mit einer Anfangsgeschwindigkeit vom Erdboden aus in die Höhe geworfen. Er erreicht eine maximale Höhe, bei der sich seine Richtung umkehrt. Von da an kehrt er im freien Fall wieder zum Erdboden zurück.
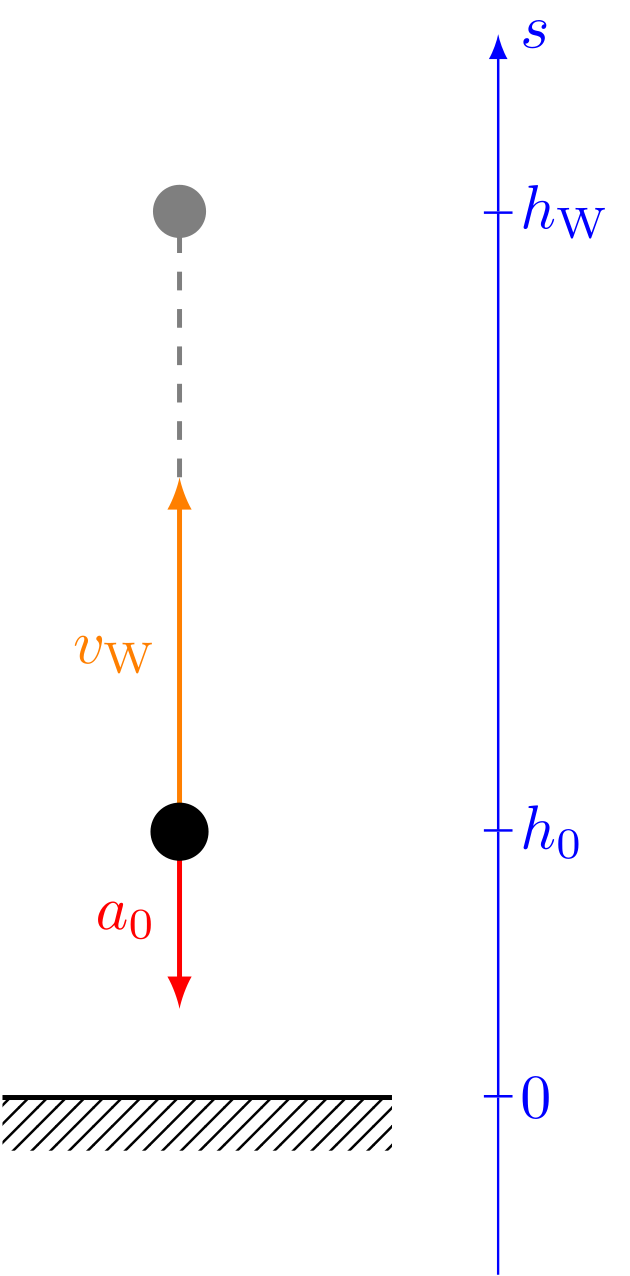
Abbildung 4.2.87: Maximale Wurfhöhe (C)
Der senkrechte Wurf beginnt mit einer Anfangsgeschwindigkeit ungleich null. Wir legen die Ortsachse wieder wie beim freien Fall senkrecht nach oben und erhalten als (Anfangs-)Bedingungen:
- Der Körper wird mit nach unten beschleunigt: .
- Er startet mit der Abwurfgeschwindigkeit : .
- Er startet am Erdboden, d.h. in der Höhe: .
Wir wollen zum einen die maximal erreichte Höhe des Körpers berechnen. Zum anderen interessiert uns die Zeitdauer bis zu deren Erreichen.
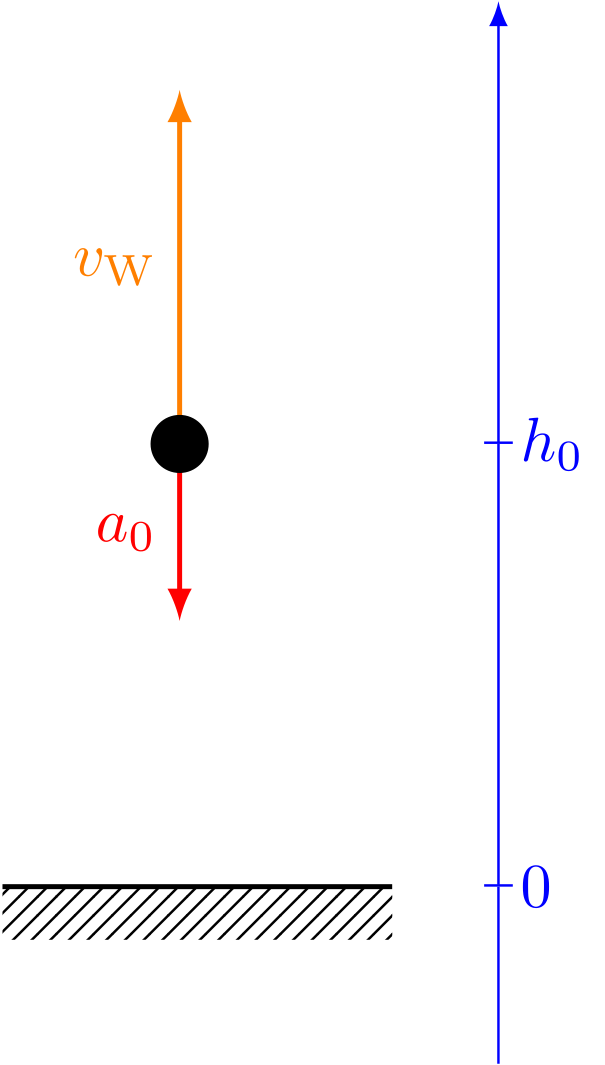
Abbildung 4.2.88: Senkrechter Wurf nach oben (C)
Die maximale Höhe ist zugleich auch der Umkehrpunkt der Bewegung. Hier ändert die Bewegung des Körpers seine Richtung und seine Geschwindigkeit ist kurzzeitig null. Die Zeit am Umkehrpunkt erhält man, indem man die Geschwindigkeitsfunktion null setzt:
Video 33: Der senkrechte Wurf: Berechnung der maximalen Wurfhöhe (C)
.
Die maximale Höhe erhält man dann, indem man die Zeit in die Ortsfunktion einsetzt:
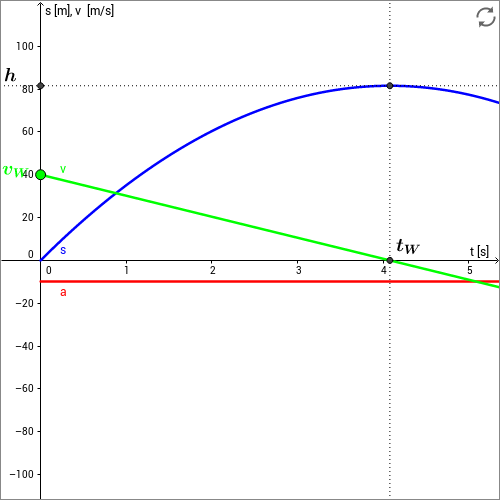
In der folgenden Skizze ist diese Rechnung nochmals visualisiert. Am Schnittpunkt der Geschwindigkeitsfunktion mit der Zeitachse, also wenn gilt , kann der Zeitpunkt abgelesen werden, an dem der Körper den Umkehrpunkt erreicht hat. Der Wert der Ortsfunktion an dieser Stelle liefert dann die maximal erreichte Höhe .
Video 34: Der senkrechte Wurf: Berechnung der Aufschlaggeschwindigkeit (C)
.
Video 35: Der senkrechte Wurf: Beispiel (C)
.
Vergleich von freiem Fall und senkrechtem Wurf (!)
Video 36: Vergleich von freiem Fall und senkrechtem Wurf (C)
.
Die Beziehung zwischen der Fallhöhe und der Aufschlaggeschwindigkeit beim freien Fall,
ist die gleiche Beziehung wie zwischen der Wurfhöhe und der Abwurfgeschwindigkeit beim senkrechten Wurf,
Dies zeigt eine gewisse Symmetrie zwischen den beiden Bewegungen. Man kann den senkrechten Wurf als zeitliche Umkehrung des freien Falls interpretieren.
Senkrechter Wurf und freier Fall sind beides Spezialfälle der eindimensionalen Bewegung mit konstanter Beschleunigung. Sie unterscheiden sich nur in den Anfangsbedingungen. Beim senkrechten Wurf ist der Körper nicht nur beim Zurückfallen zur Erdoberfläche, sondern auch schon beim Hochsteigen der konstanten Erdbeschleunigung ausgesetzt. Am Umkehrpunkt der Bewegung ändert sich diese Beschleunigung nicht! Der Körper befindet sich also auch schon beim Hochsteigen im „freien Fall“.
Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie .
Falls nicht anders angegeben, verwenden Sie

