4.2.1 Geschwindigkeit und Beschleunigung
Für dieses Thema ist der Begriff der Ableitung von zentraler Bedeutung, der z.B. im
Onlinekurs Mathematik, Kapitel 7 behandelt wird.
Zu Illustration der Begriffe Geschwindigkeit und Beschleunigung greifen wir hier der Einführung der geradlinigen Bewegungen im Lektionstext Abschnitt 4.2.2 ein wenig vor. Dabei betrachten wir zunächst die im folgenden dargestellten Zusammenhänge als experimentell gegeben. Eine Herleitung folgt in Abschnitt 4.2.2.
Basiswissen „Gleichförmige Bewegung“
In diesem Abschnitt werden wir ein bisher unbekanntes Zeichen verwenden. Dieses Zeichen (, gesprochen: Delta, ist der vierte Buchstabe des griechischen Alphabets als Großbuchstabe) steht im Allgemeinen für eine Differenz zwischen zwei Werten. In der folgenden Abbildung ist dies veranschaulicht. und bezeichnen zwei Zeitpunkte. Für das Zeitfenster zwischen diesen beiden Zeitpunkten schreibt man üblicherweise . Ebenso kann diese Schreibweise für andere Differenzen verwendet werden. und kennzeichnen zwei beliebige Ortspunkte. Für das Wegstück dazwischen kann geschrieben werden: .
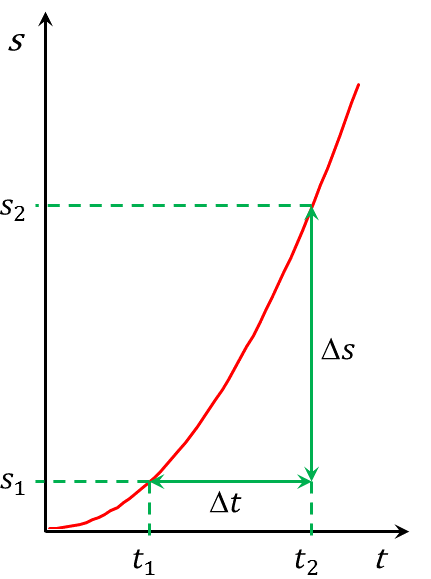
Abbildung 4.2.1: Erklärung des Zeichens (C)
Legt ein Körper in gleichen Zeiten gleiche Wege zurück, spricht man von einer gleichförmigen Bewegung. Verdoppelt sich der zurückgelegte Weg , dann verdoppelt sich ebenfalls die benötigte Zeit . Der zurückgelegte Weg und die benötigte Zeit sind zueinander proportional.
Der Quotient aus Wegstrecke und Zeitintervall wird als Geschwindigkeit bezeichnet und ändert sich
während der Bewegung nicht:
Die Einheit der Geschwindigkeit ist: .
Die Einheit der Geschwindigkeit ist: .
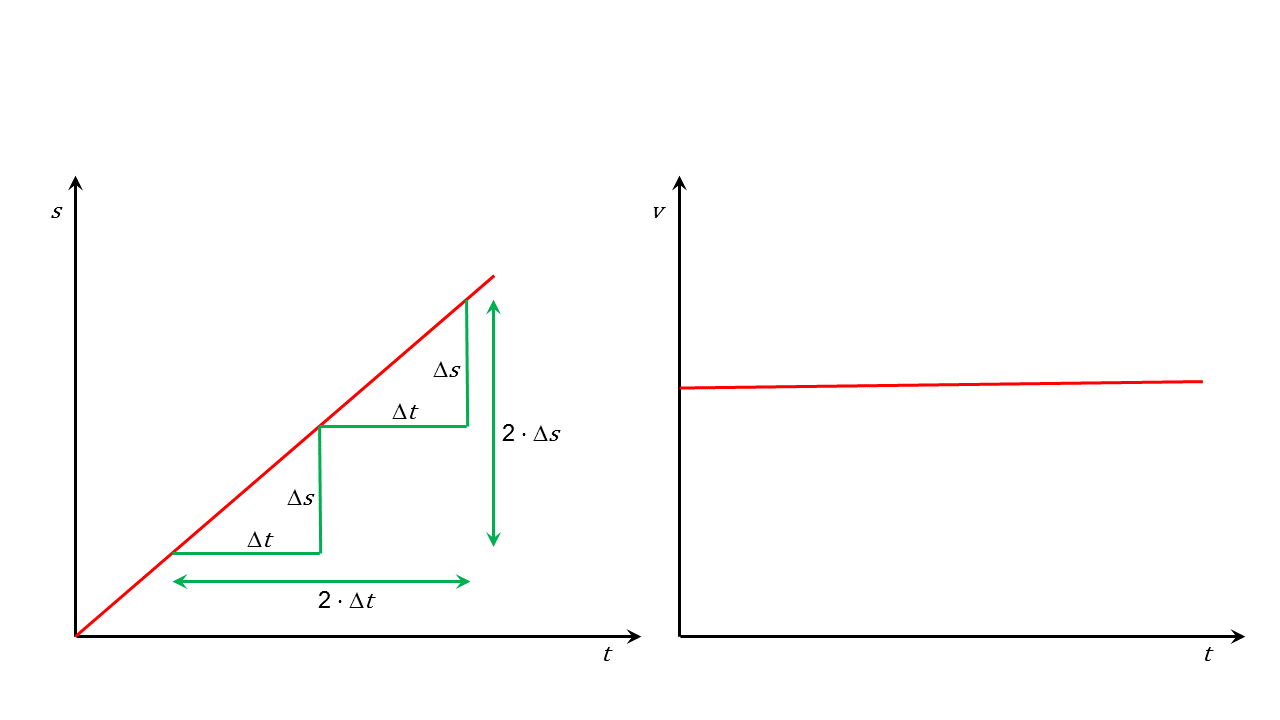
Abbildung 4.2.2: Gleichförmige Bewegung (C)
Sind zwei der drei Größen bekannt, kann mit diesen und der obenstehenden Gleichung die dritte berechnet werden. Diese Überlegungen gelten so auch für nicht geradlinige Bewegungen.
Beispiel
4.2.1
Ein Auto legt in einer Zeit von eine Strecke von zurück. Wie groß war seine Durchschnittsgeschwindigkeit ?
Der Querstrich über der Geschwindigkeit gibt an, dass es sich um eine mittlere Geschwindigkeit handelt. Das Auto ist während seiner Tour sicher nicht konstant mit der Geschwindigkeit von gefahren, sondern manchmal etwas schneller oder auch etwas langsamer.
Ein Auto legt in einer Zeit von eine Strecke von zurück. Wie groß war seine Durchschnittsgeschwindigkeit ?
Der Querstrich über der Geschwindigkeit gibt an, dass es sich um eine mittlere Geschwindigkeit handelt. Das Auto ist während seiner Tour sicher nicht konstant mit der Geschwindigkeit von gefahren, sondern manchmal etwas schneller oder auch etwas langsamer.
Beispiel
4.2.2
Die Lichtgeschwindigkeit beträgt etwa . Licht braucht für seinen Weg von der Sonne bis zu unserem Planeten etwa . Wie weit ist die Sonne von uns entfernt?
Tatsächlich liegt der mittlere Abstand bei Millionen Kilometer.
Die Lichtgeschwindigkeit beträgt etwa . Licht braucht für seinen Weg von der Sonne bis zu unserem Planeten etwa . Wie weit ist die Sonne von uns entfernt?
Tatsächlich liegt der mittlere Abstand bei Millionen Kilometer.
Beispiel
4.2.3
Der Mond bewegt sich mit einer Geschwindigkeit von um die Erde. Es soll die Umlaufzeit des Mondes um die Erde berechnet werden. Der Einfachheit halber nehmen wir an, die Bahn sei eine Kreisbahn mit dem Radius . Zuerst muss die Länge der Kreisbahn berechnet werden:
Zur Berechnung der Umlaufzeit formen wir die Gleichung nach der Zeit um. Der zurückgelegte Weg entspricht dem Kreisumfang :
Die genaue Umlaufzeit liegt bei .
Der Mond bewegt sich mit einer Geschwindigkeit von um die Erde. Es soll die Umlaufzeit des Mondes um die Erde berechnet werden. Der Einfachheit halber nehmen wir an, die Bahn sei eine Kreisbahn mit dem Radius . Zuerst muss die Länge der Kreisbahn berechnet werden:
Zur Berechnung der Umlaufzeit formen wir die Gleichung nach der Zeit um. Der zurückgelegte Weg entspricht dem Kreisumfang :
Die genaue Umlaufzeit liegt bei .
Basiswissen „Gleichmäßig beschleunigte Bewegung“
Unter einer gleichmäßig beschleunigten Bewegung versteht man eine Bewegung, bei der ein Körper einer konstanten Beschleunigung ausgesetzt ist. Die Geschwindigkeit wird dabei mit zunehmender Zeit immer größer. Dabei ist die Geschwindigkeitszunahme in gleich lang dauernden Zeitintervallen immer gleich groß, d.h. die Geschwindigkeit ist proportional zur Zeit.
Für den Proportionalitätsfaktor gilt: .
Für die Beziehung zwischen Weg und Zeit ergibt sich ein zusätzlicher quadratischer Term: .
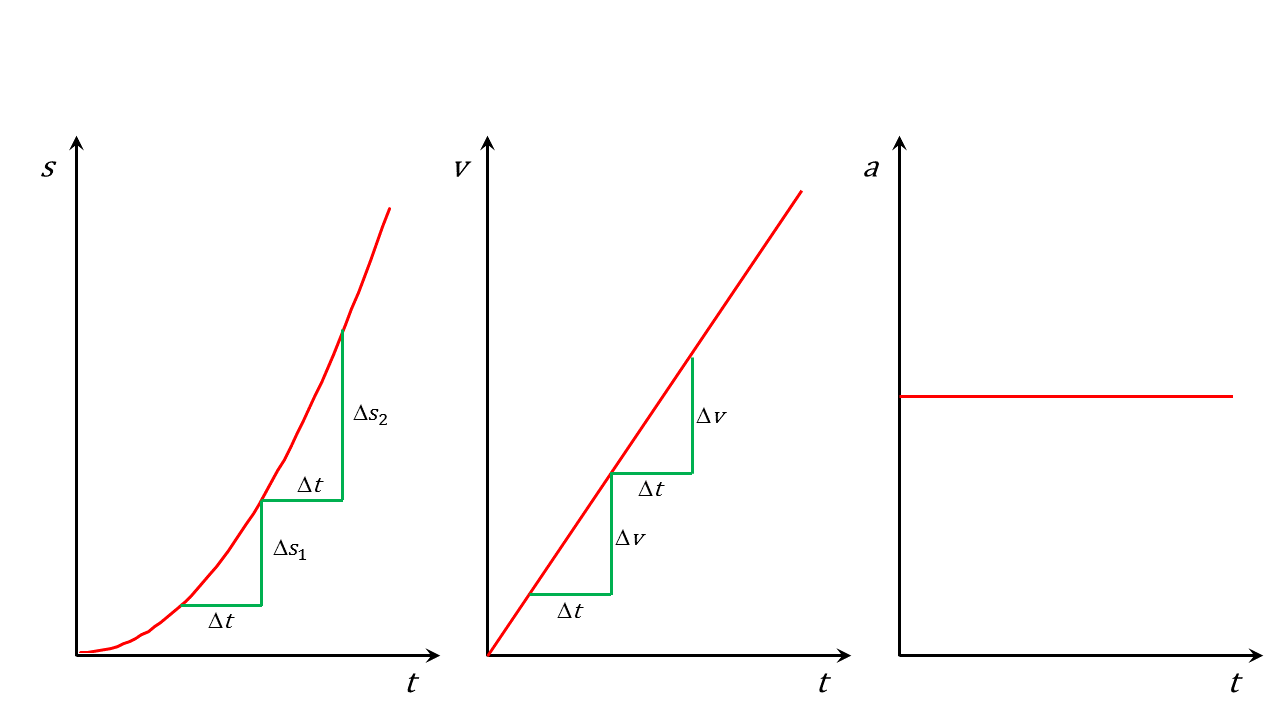
Abbildung 4.2.3: Diagramme für eine gleichmäßig beschleunigte Bewegung (C)
Bei einer gleichmäßig beschleunigten Bewegung können zwei Fälle unterschieden werden. Der Einfachheit halber nehmen wir bei unseren Überlegungen an, dass sich die Beschleunigung spontan von null auf den gewünschten Wert ändert. Dies entspricht zwar nicht der Realität, aber es erleichtert das Verständnis der Sachverhalte.
Fall 1:
Der Körper wird aus der Ruhe heraus beschleunigt. Die Diagramme, die eine solche Bewegung kennzeichnen, sind identisch mit den obigen Diagrammen. Als --Diagramm ergibt sich eine Ursprungsgerade mit Steigung und als --Diagramm erhält man eine Parabel durch den Ursprung.
Wird der Körper aus der Ruhe heraus beschleunigt, entspricht die Geschwindigkeitsänderung der erreichten Geschwindigkeit
und für den zurückgelegten Weg gilt
und für den zurückgelegten Weg gilt
Beispiel
4.2.4
Ein Auto fährt mit einer konstanten Beschleunigung von an. Welche Geschwindigkeit hat es nach erreicht und welchen Weg hat es zurückgelegt?
Mit Hilfe der beiden Gleichungen kann die Lösung berechnet werden. Für die Geschwindigkeit ergibt sich
und die zurückgelegte Wegstrecke liegt bei
Hier muss beachtet werden, dass sowohl der Zahlenwert als auch die Einheit quadriert werden müssen.
Ein Auto fährt mit einer konstanten Beschleunigung von an. Welche Geschwindigkeit hat es nach erreicht und welchen Weg hat es zurückgelegt?
Mit Hilfe der beiden Gleichungen kann die Lösung berechnet werden. Für die Geschwindigkeit ergibt sich
und die zurückgelegte Wegstrecke liegt bei
Hier muss beachtet werden, dass sowohl der Zahlenwert als auch die Einheit quadriert werden müssen.
Beispiel
4.2.5
Aus dem Stand beschleunigt ein Auto lang und erreicht eine Geschwindigkeit von . Wie groß ist die Beschleunigung und der zurückgelegte Weg ? Geben Sie die Ergebnisse in SI-Einheiten an. Zur Lösung des Problems muss zuerst die Geschwindigkeit in angeben werden:
Für die Beschleunigung formen wir die Gleichung für die Geschwindigkeit um und es ergibt sich
Damit kann der Weg berechnet werden:
Bei dieser Aufgabe ist es wichtig, dass die Einheiten umgerechnet werden. Die Umrechnung der Größen in SI-Einheiten macht man am besten zu Beginn der Rechnung.
Aus dem Stand beschleunigt ein Auto lang und erreicht eine Geschwindigkeit von . Wie groß ist die Beschleunigung und der zurückgelegte Weg ? Geben Sie die Ergebnisse in SI-Einheiten an. Zur Lösung des Problems muss zuerst die Geschwindigkeit in angeben werden:
Für die Beschleunigung formen wir die Gleichung für die Geschwindigkeit um und es ergibt sich
Damit kann der Weg berechnet werden:
Bei dieser Aufgabe ist es wichtig, dass die Einheiten umgerechnet werden. Die Umrechnung der Größen in SI-Einheiten macht man am besten zu Beginn der Rechnung.
Fall 2:
Der Körper bewegt sich mit einer Anfangsgeschwindigkeit und führt eine gleichförmige Bewegung aus. Zu Beginn der Beschleunigung hat der Körper dann schon eine Strecke zurückgelegt und wird aus der Bewegung heraus beschleunigt. Jeder kennt diesen Fall aus dem täglichen Leben. Man fährt auf der Autobahn und möchte dann ein langsameres Fahrzeug überholen.
In der Abbildung ist so ein Vorgang schematisch dargestellt. Im Zeitraum vor ergeben sich die gleichen Diagramme wie bei einer gleichförmigen Bewegung. Das Auto fährt konstant. Dann fängt der Überholvorgang an und eine gleichmäßig beschleunigte Bewegung kommt zur gleichförmigen Bewegung hinzu.
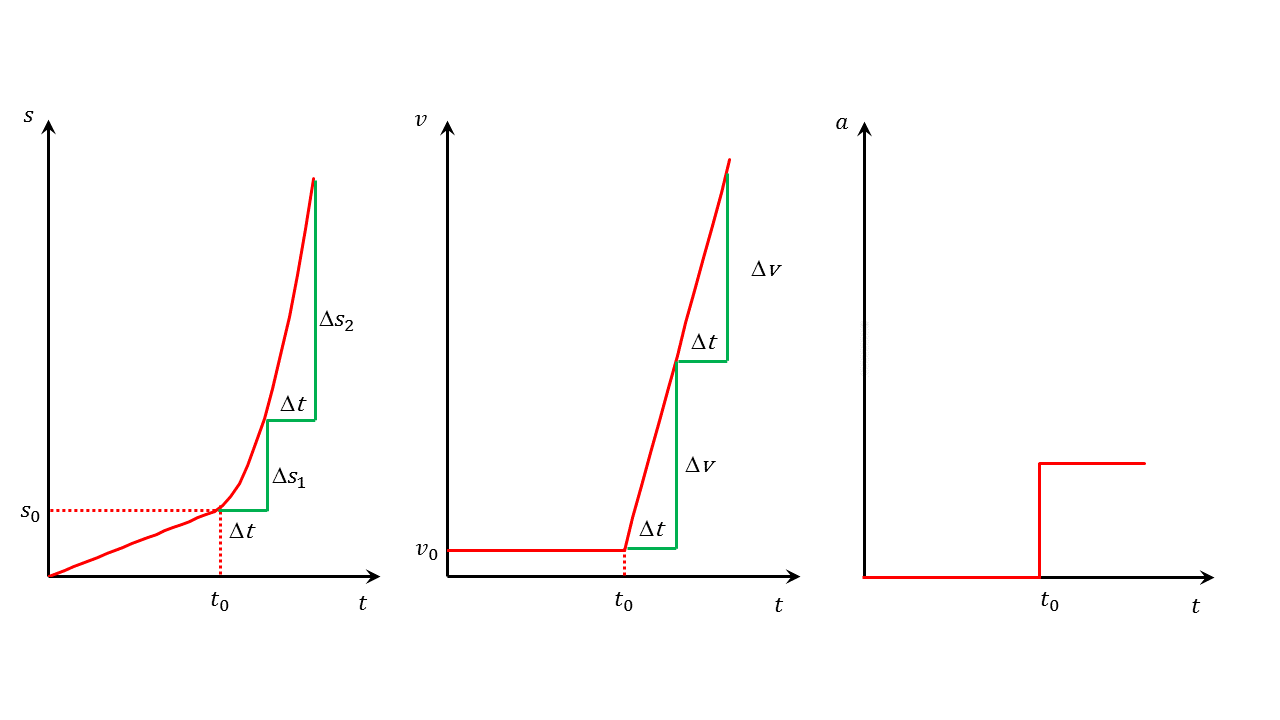
Abbildung 4.2.4: Diagramme für eine gleichmäßig beschleunigte Bewegung mit Anfangsgeschwindigkeit (C)
Um hier eine Aussage über die erreichte Geschwindigkeit oder den zurückgelegten Weg machen zu können, müssen die beiden bisher verwendeten Gleichungen etwas modifiziert werden. Der Einfachheit halber wird der Nullpunkt der Zeitrechnung auf den Wert gelegt. Der Körper bewegt sich schon mit einer Geschwindigkeit . Jetzt kommt die Beschleunigung hinzu und verursacht eine Änderung der Geschwindigkeit.
Es ergibt sich für die Geschwindigkeit zu einem Zeitpunkt :
Für die zu einem Zeitpunkt zurückgelegte Wegstrecke erhält man:
- : der Punkt, an dem die Beschleunigung zum Zeitpunkt startet, bzw. der bereits zurückgelegte Weg.
- : die Geschwindigkeit, mit der sich der Körper gleichförmig bewegt, bevor die Beschleunigung einsetzt. Diese muss auch während des Beschleunigungsvorganges berücksichtigt werden und trägt auch weiter zum zurückgelegten Weg bei.
- : der durch die Beschleunigung zurückgelegte Weg.
Beispiel
4.2.6
Ein Auto fährt in der Stadt mit einer konstanten Geschwindigkeit von . Am Ortsende beschleunigt der Fahrer mit , bis eine Geschwindigkeit von erreicht ist. Wie lange dauert der Beschleunigungsvorgang und welche Strecke legt das Fahrzeug währenddessen zurück?
Als Erstes werden die gegebenen Größen in SI-Einheiten umgerechnet:
Jetzt liegen alle Größen in SI-Einheiten vor und die Dauer der Beschleunigung kann bestimmt werden:
Im Anschluss wird die zweite Gleichung zur Berechnung des zurückgelegten Weges herangezogen. Da nur der Beschleunigungsvorgang von Interesse ist, kann für den Startpunkt gesetzt werden:
Ein Auto fährt in der Stadt mit einer konstanten Geschwindigkeit von . Am Ortsende beschleunigt der Fahrer mit , bis eine Geschwindigkeit von erreicht ist. Wie lange dauert der Beschleunigungsvorgang und welche Strecke legt das Fahrzeug währenddessen zurück?
Als Erstes werden die gegebenen Größen in SI-Einheiten umgerechnet:
Jetzt liegen alle Größen in SI-Einheiten vor und die Dauer der Beschleunigung kann bestimmt werden:
Im Anschluss wird die zweite Gleichung zur Berechnung des zurückgelegten Weges herangezogen. Da nur der Beschleunigungsvorgang von Interesse ist, kann für den Startpunkt gesetzt werden:
Beispiel
4.2.7
Der Fahrer aus obigem Beispiel muss eine Vollbremsung machen, da ein Reh vor ihm auf die Fahrbahn springt. Wie groß muss die Verzögerung sein, damit das Fahrzeug direkt vor dem Tier zum Stehen kommt? Und wie lange dauert der Bremsvorgang?
Da das Auto hier zum Stillstand kommt, liegt die Endgeschwindigkeit bei und die Ausgangsgeschwindigkeit bei . Der Bremsweg, der zur Verfügung steht, beträgt . Der Weg, der vor Beginn des Bremsvorganges zurückgelegt wurde, ist für die Fragestellung nicht von Bedeutung. Zur Lösung dieses Problems setzt man daher den Weg .
Die Schwierigkeit der Aufgabe liegt darin, dass die gesuchten Größen und jeweils in beiden Gleichungen vorkommen. Deshalb wird jetzt eine Gleichung nach einer der gesuchten Variablen aufgelöst:
Dieses Ergebnis wird jetzt in die zweite Gleichung eingesetzt:
Jetzt ist die für den Bremsvorgang benötigte Zeit bekannt, und mit diesem Ergebnis kann dann auch die Verzögerung berechnet werden:
Alternativ hätte man die Geschwindigkeitsgleichung auch erst nach der Zeit auflösen und diese dann in die Weggleichung einsetzen können.
Der Fahrer aus obigem Beispiel muss eine Vollbremsung machen, da ein Reh vor ihm auf die Fahrbahn springt. Wie groß muss die Verzögerung sein, damit das Fahrzeug direkt vor dem Tier zum Stehen kommt? Und wie lange dauert der Bremsvorgang?
Da das Auto hier zum Stillstand kommt, liegt die Endgeschwindigkeit bei und die Ausgangsgeschwindigkeit bei . Der Bremsweg, der zur Verfügung steht, beträgt . Der Weg, der vor Beginn des Bremsvorganges zurückgelegt wurde, ist für die Fragestellung nicht von Bedeutung. Zur Lösung dieses Problems setzt man daher den Weg .
Die Schwierigkeit der Aufgabe liegt darin, dass die gesuchten Größen und jeweils in beiden Gleichungen vorkommen. Deshalb wird jetzt eine Gleichung nach einer der gesuchten Variablen aufgelöst:
Dieses Ergebnis wird jetzt in die zweite Gleichung eingesetzt:
Jetzt ist die für den Bremsvorgang benötigte Zeit bekannt, und mit diesem Ergebnis kann dann auch die Verzögerung berechnet werden:
Alternativ hätte man die Geschwindigkeitsgleichung auch erst nach der Zeit auflösen und diese dann in die Weggleichung einsetzen können.
Unter dem folgenden Link finden Sie eine Animation, die Ihnen erlaubt, mit verschiedenen Startwerten eine gleichförmige Bewegung, eine gleichmäßig beschleunigte Bewegung oder einen Bremsvorgang zu simulieren:
Animation zur gleichmäßig beschleunigten Bewegung
Wenn in den folgenden Aufgabentexten nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie
Aufgabe 4.2.8
Unter welchen Bedingungen ist eine Bewegung gleichförmig?
Unter welchen Bedingungen ist eine Bewegung gleichförmig?
| In gleichen Zeiten werden gleiche Strecken zurückgelegt | |
| Die Anfangsgeschwindigkeit ist null | |
| Der Geschwindigkeitsbetrag ändert sich mit der Zeit | |
| Die Bewegung findet nur in eine Richtung statt |
Aufgabe 4.2.9
Eine Schnecke kriecht im Durchschnitt mit einer Geschwindigkeit von durch die Welt. Wieviele Minuten braucht sie, um einen Salatkopf, der von ihr entfernt ist, zu erreichen?

Eine Schnecke kriecht im Durchschnitt mit einer Geschwindigkeit von durch die Welt. Wieviele Minuten braucht sie, um einen Salatkopf, der von ihr entfernt ist, zu erreichen?
Aufgabe 4.2.10
Das schnellste Landtier, der Gepard, erreicht eine Geschwindigkeit von bis zu . Welche Strecke legt er zurück, wenn er lang sprintet?
Das schnellste Landtier, der Gepard, erreicht eine Geschwindigkeit von bis zu . Welche Strecke legt er zurück, wenn er lang sprintet?
Aufgabe 4.2.11
Ein Motorradfahrer fährt lang mit einer Geschwindigkeit von eine gerade Strecke entlang. Schlagartig ändert er seine Geschwindigkeit auf (in der realen Welt ist dies natürlich nicht möglich). Mit dieser Geschwindigkeit fährt er weiter. Dann macht er eine Pause und bleibt für stehen. Nach seiner Pause dreht er um und fährt mit einer Geschwindigkeit von an seinen Startpunkt zurück. Wie lange braucht er für die Rückfahrt?
Ein Motorradfahrer fährt lang mit einer Geschwindigkeit von eine gerade Strecke entlang. Schlagartig ändert er seine Geschwindigkeit auf (in der realen Welt ist dies natürlich nicht möglich). Mit dieser Geschwindigkeit fährt er weiter. Dann macht er eine Pause und bleibt für stehen. Nach seiner Pause dreht er um und fährt mit einer Geschwindigkeit von an seinen Startpunkt zurück. Wie lange braucht er für die Rückfahrt?
Aufgabe 4.2.12
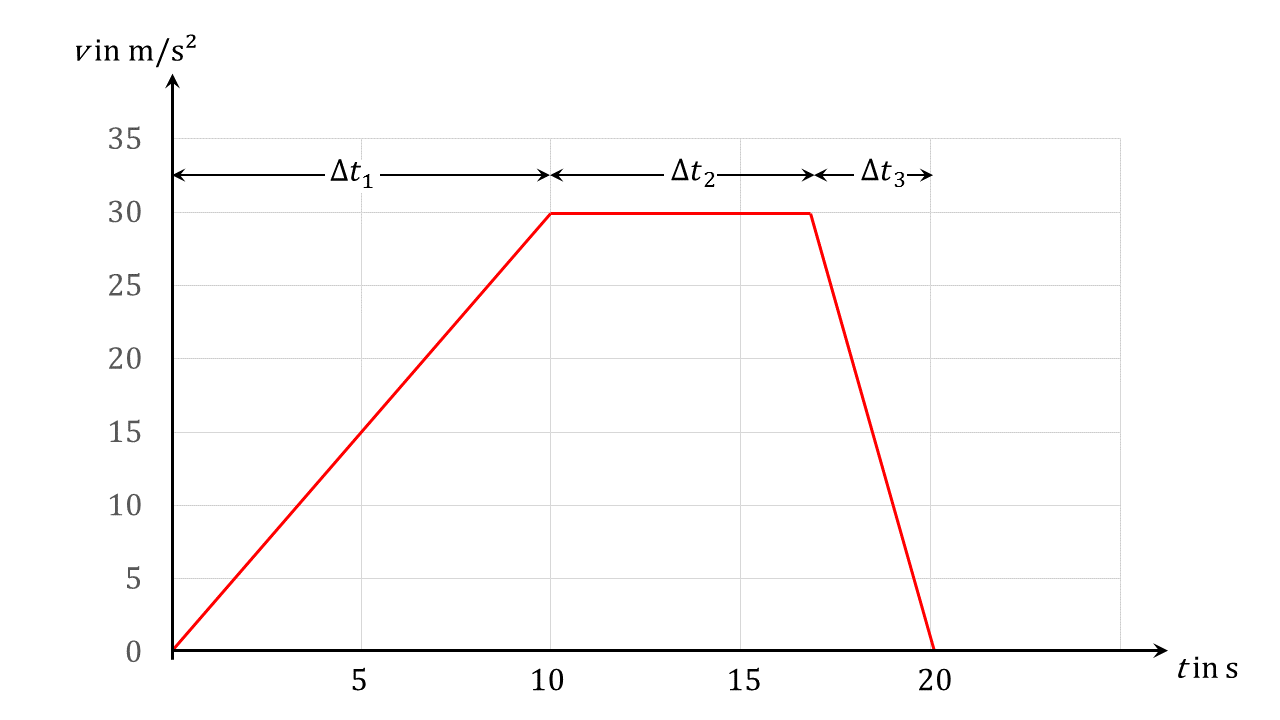
Für ein Fahrzeug wurde das untenstehende Beschleunigungs-Zeit-Diagramm aufgenommen. Zum Zeitpunkt und nach ist das Fahrzeug in Ruhe. Welche Art von Bewegung führt das Fahrzeug in den drei Zeitabschnitten aus? Interpretieren Sie das -Diagramm.
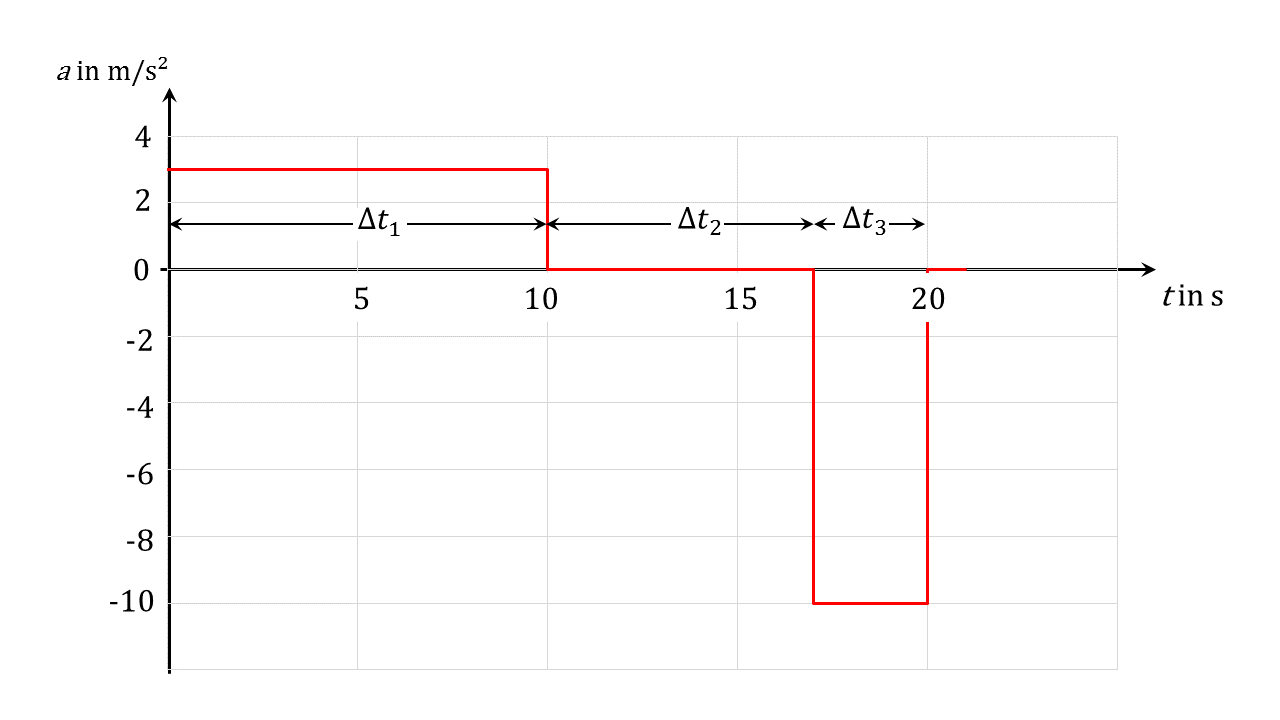
Im Zeitfenster liegt eine vor.
Im Zeitfenster liegt eine vor.
Im Zeitfenster liegt eine vor.
Für ein Fahrzeug wurde das untenstehende Beschleunigungs-Zeit-Diagramm aufgenommen. Zum Zeitpunkt und nach ist das Fahrzeug in Ruhe. Welche Art von Bewegung führt das Fahrzeug in den drei Zeitabschnitten aus? Interpretieren Sie das -Diagramm.

Abbildung 4.2.5: Skizze (C)
Im Zeitfenster liegt eine vor.
Im Zeitfenster liegt eine vor.
Im Zeitfenster liegt eine vor.
Aufgabe 4.2.13
Für ein Fahrzeug wurde untenstehendes Beschleunigungs-Zeit-Diagramm aufgenommen. Zum Zeitpunkt und nach ist das Fahrzeug in Ruhe. Wie hoch ist die Höchstgeschwindigkeit des Fahrzeugs und die insgesamt zurückgelegte Wegstrecke ?

Für ein Fahrzeug wurde untenstehendes Beschleunigungs-Zeit-Diagramm aufgenommen. Zum Zeitpunkt und nach ist das Fahrzeug in Ruhe. Wie hoch ist die Höchstgeschwindigkeit des Fahrzeugs und die insgesamt zurückgelegte Wegstrecke ?

Abbildung 4.2.7: Skizze (C)
| ; | |
| ; | |
| ; das Fahrzeug legt keinen Weg zurück. | |
| ; |
Aufgabe 4.2.14
Ein Auto wird aus dem Stand mit beschleunigt. Welchen Weg hat es nach zurückgelegt? Geben Sie Ihre Lösung in an.

Ein Auto wird aus dem Stand mit beschleunigt. Welchen Weg hat es nach zurückgelegt? Geben Sie Ihre Lösung in an.
Aufgabe 4.2.15
Ein Auto wird aus dem Stand für mit einer Beschleunigung von beschleunigt. Welche Geschwindigkeit erreicht es?
Ein Auto wird aus dem Stand für mit einer Beschleunigung von beschleunigt. Welche Geschwindigkeit erreicht es?
| Ein Auto kann gar nicht so schnell beschleunigen. | |
Aufgabe 4.2.16
Ein Auto hat zum Zeitpunkt eine Geschwindigkeit von und wird dann gleichmäßig mit abgebremst. Nach wieviel Sekunden beträgt die Geschwindigkeit nur noch ?

Ein Auto hat zum Zeitpunkt eine Geschwindigkeit von und wird dann gleichmäßig mit abgebremst. Nach wieviel Sekunden beträgt die Geschwindigkeit nur noch ?
Aufgabe 4.2.17
Ein Körper beschleunigt aus der Ruhe heraus mit einer konstanten Beschleunigung. Nach einer Strecke erreicht er eine Geschwindigkeit von . Wie lange braucht er für diesen Beschleunigungsvorgang?
Ein Körper beschleunigt aus der Ruhe heraus mit einer konstanten Beschleunigung. Nach einer Strecke erreicht er eine Geschwindigkeit von . Wie lange braucht er für diesen Beschleunigungsvorgang?
Aufgabe 4.2.18
Ein Körper beschleunigt aus der Ruhe heraus mit einer konstanten Beschleunigung. Nach einer Strecke erreicht er eine Geschwindigkeit von . Wie groß ist die Beschleunigung ?
Ein Körper beschleunigt aus der Ruhe heraus mit einer konstanten Beschleunigung. Nach einer Strecke erreicht er eine Geschwindigkeit von . Wie groß ist die Beschleunigung ?
Massenpunkte (!)
Video 1: Massenpunkte (C)
.
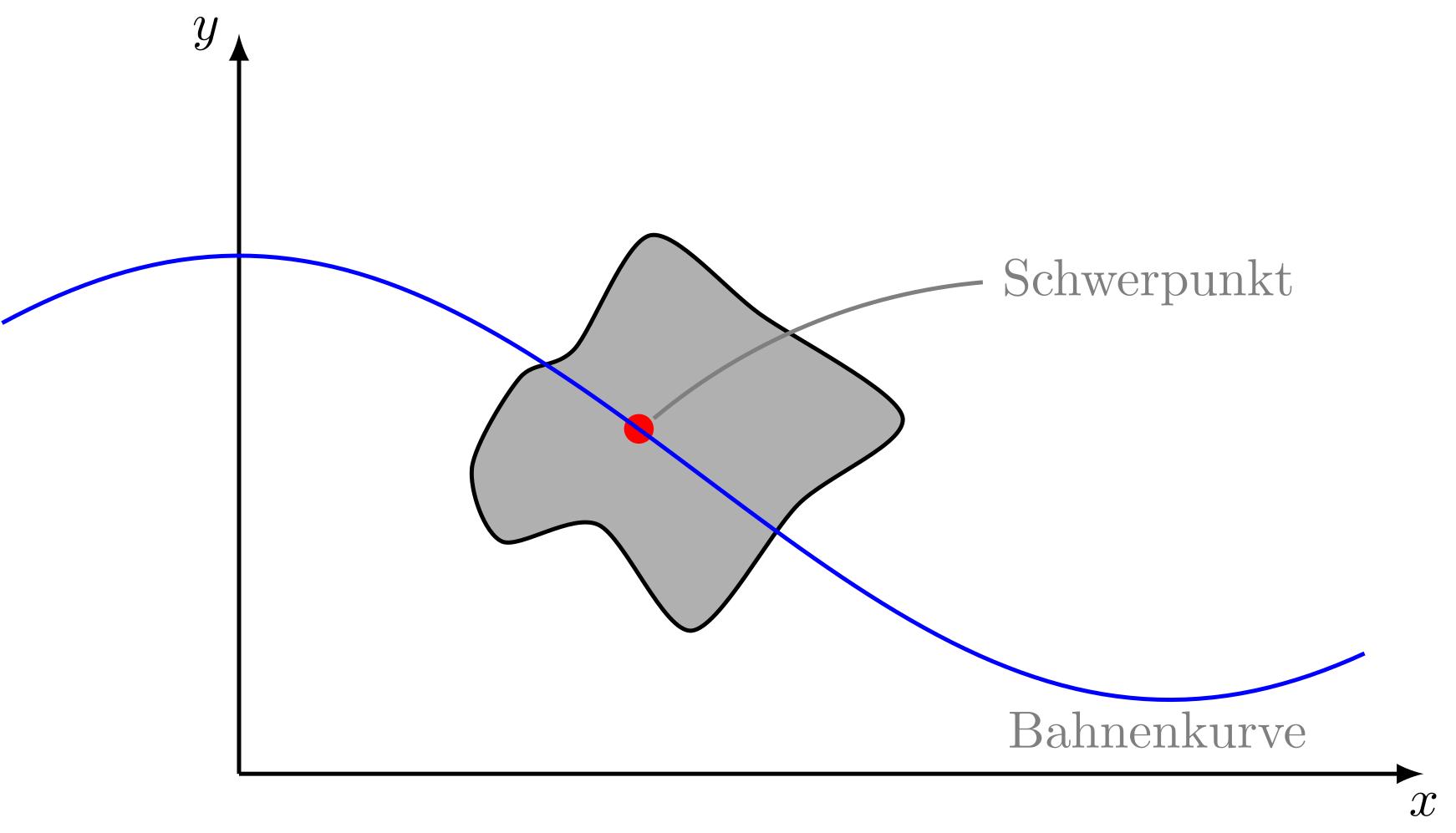
Abbildung 4.2.8: Beschreibung der Bewegung eines ausgedehnten Körpers anhand des Schwerpunkts (C)
In diesem Abschnitt werden die Bewegungen mit Hilfe sogenannter Massenpunkte beschrieben. Man versteht darunter eine Masse ohne Ausdehnung. Die gesamte Masse ist also in einem unendlich kleinen Massenpunkt konzentriert. In der Natur kennen wir nur ausgedehnte Körper (mit Ausnahme der Elementarteilchen, der kleinsten Bausteine der Materie). Man kann aber zeigen, dass die Bewegung eines ausgedehnten Körpers immer in die Bewegung seines Schwerpunkts und eine Drehung um diesen Schwerpunkt aufgeteilt werden kann. Die Definition des Schwerpunkts und die Beschreibung der Drehungen finden Sie in späteren Abschnitten. Es werden also zunächst die Bewegungsgesetze für die idealisierten Massenpunkte betrachtet. Später können wir sie dann direkt auf die Bewegung des Schwerpunkts ausgedehnter Objekte übertragen.
Geschwindigkeit (!)
Video 2: Geschwindigkeit: Durchschnittsgeschwindigkeit (C)
.

Abbildung 4.2.9: Zurückgelegter Weg eines Punktes (C)
Video 3: Geschwindigkeit: Beispiel (C)
.
Video 4: Geschwindigkeit: Beispiel (C)
.
Video 5: Geschwindigkeit: Weg-Zeit-Diagramm (C)
.
Oben wurde eine Durchschnittsgeschwindigkeit definiert.
Dabei wird eine mittlere Geschwindigkeit für eine ausgewählte Zeitdauer und die in dieser Zeit zurückgelegte Strecke bestimmt.
Dies wird in der folgenden Skizze illustriert.
Zwischen den beiden Punkten und wird der obige Quotient gebildet und als Steigungsdreieck dargestellt.
Die berechnete Geschwindigkeit ist aber nicht die Geschwindigkeit an den Orten oder ,
sondern die mittlere Geschwindigkeit.
Da die Streckenzunahme nicht proportional zur Zeit ist, ist die Geschwindigkeit am Anfang () höher und am Ende ()
niedriger als die Durchschnittsgeschwindigkeit.
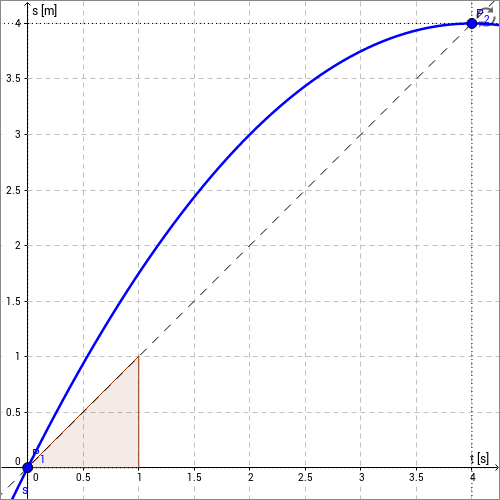 Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)

Video 6: Geschwindigkeit: Momentangeschwindigkeit (C)
.
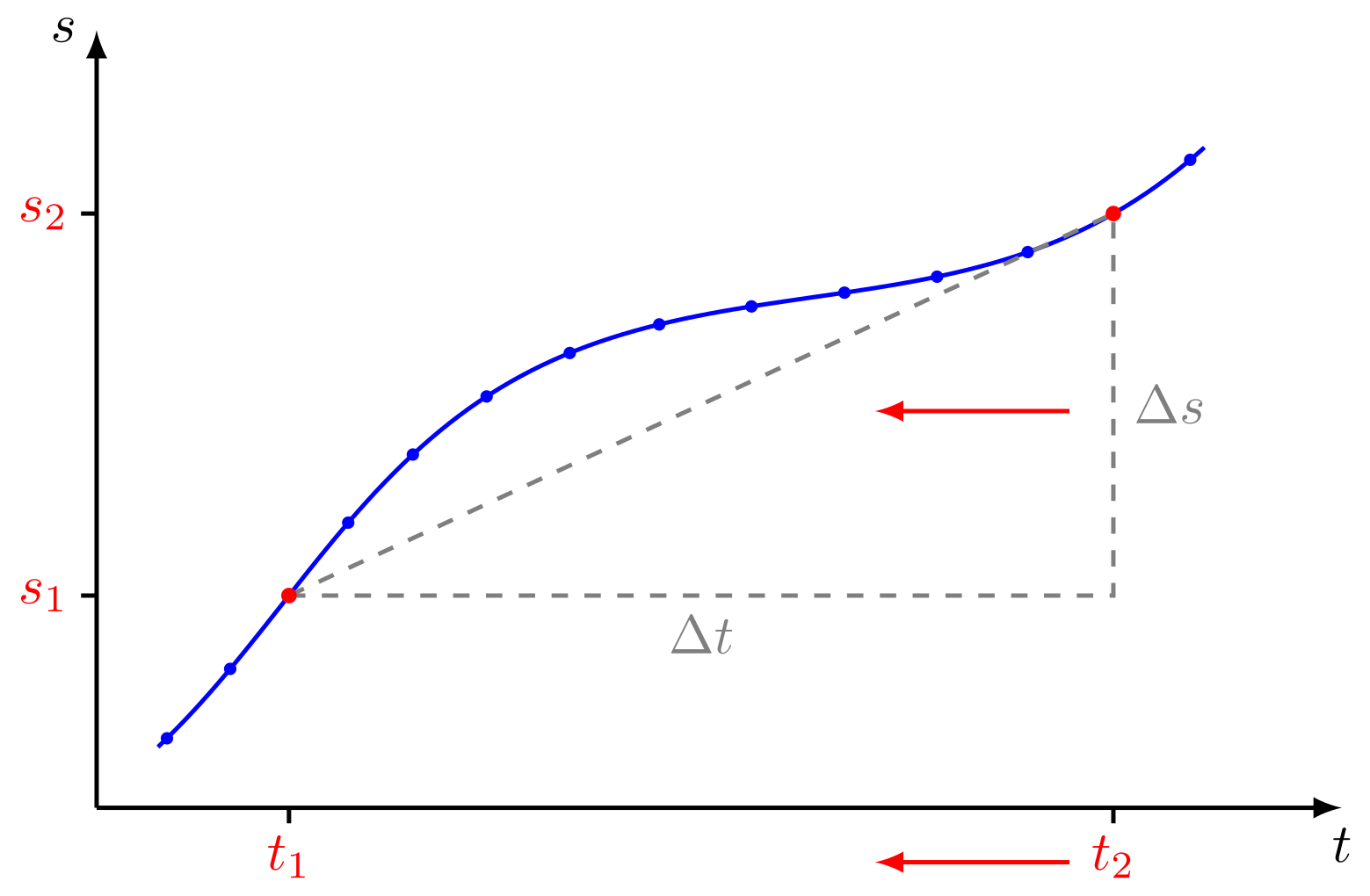
Abbildung 4.2.11: Zeitdifferenz läuft gegen Null, um Momentangeschwindigkeit anzunähern (C)
Da die Geschwindigkeit in der Regel nicht konstant ist, ersetzt man den oben definierten Quotienten aus Orts- und
Zeitdifferenzen durch die Ableitung der Ortsfunktion nach der Zeit.
Dies nennt man die Momentangeschwindigkeit zum Zeitpunkt :
Diese Definition der Momentangeschwindigkeit ist in der folgenden Skizze illustriert. An einem beliebigen Punkt der Ortsfunktion (blaue Kurve) kann die Ableitung gebildet werden. Diese entspricht der Steigung der Ortsfunktion in diesem Punkt und ist als Steigungsdreieck eingezeichnet. Die Steigung ist die Momentangeschwindigkeit an diesem Punkt und gesondert als Wert aufgetragen (grünes Kreuz auf grüner Kurve). Bewegen Sie den Punkt (blau) und machen Sie sich so die Bedeutung der Momentangeschwindigkeit klar. Die Geschwindigkeitsfunktion ist die Ableitung der Ortsfunktion nach der Zeit. Der Wert der Geschwindigkeit kann auch negativ werden. In diesem Falle bewegt sich der Körper in umgekehrter Richtung.
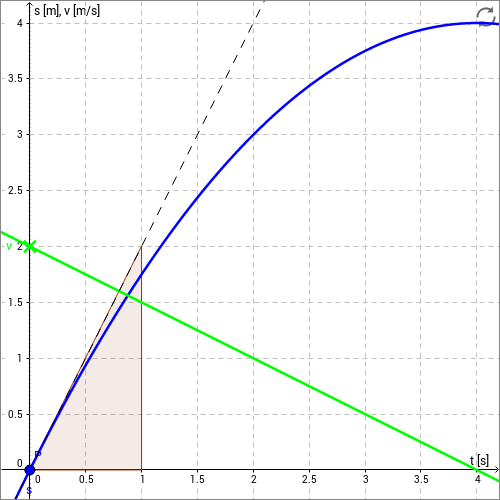
Wenn nicht anders angegeben, versteht man unter dem Begriff Geschwindigkeit üblicherweise die Momentangeschwindigkeit eines Körpers.
Video 7: Geschwindigkeit: Beispiel (C)
.
Video 8: Geschwindigkeit: Beispiel (C)
.
Video 9: Geschwindigkeit: Beispiel (C)
.
Video 10: Geschwindigkeit: Beispiel (C)
.
Video 11: Geschwindigkeit: Beispiel (C)
.
Beschleunigung (!)
Video 12: Beschleunigung: Definition Momentanbeschleunigung (C)
.
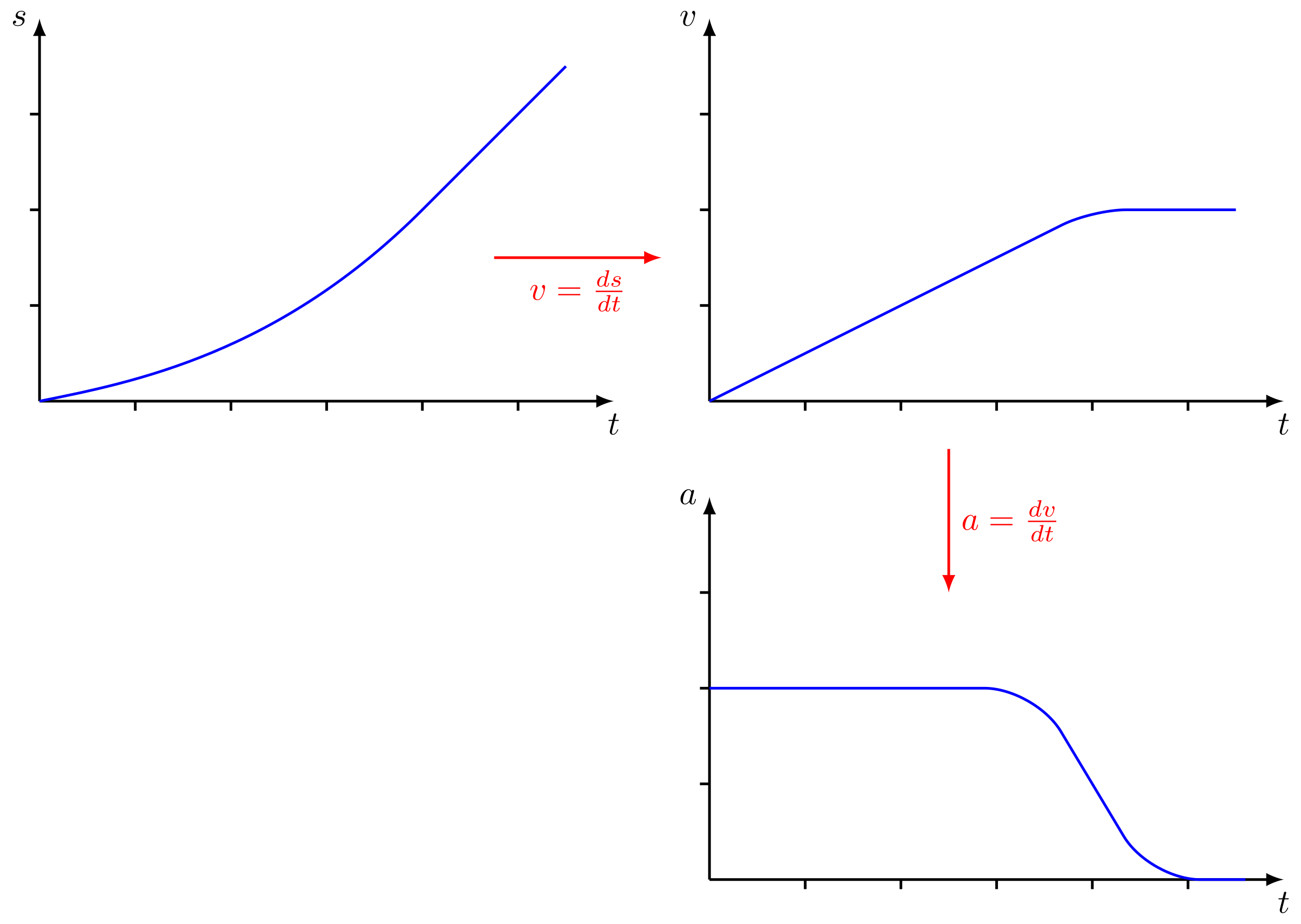
Abbildung 4.2.13: Weg, Geschwindigkeit und Beschleunigung als Funktion der Zeit (C)
Ein Körper wird beschleunigt, wenn sich die Geschwindigkeit als Funktion der Zeit ändert.
Daher wird die Beschleunigung als Ableitung der Geschwindigkeitsfunktion nach der Zeit definiert:
Die Beschleunigung ist also die erste Ableitung der Geschwindigkeit nach der Zeit. Damit ist sie aber auch die zweite Ableitung des Ortes nach der Zeit:
Die Beschleunigung ist also die erste Ableitung der Geschwindigkeit nach der Zeit. Damit ist sie aber auch die zweite Ableitung des Ortes nach der Zeit:
Video 13: Beschleunigung: Definition Durchschnittsbeschleunigung (C)
.
Auch bei der Beschleunigung kann man eine Durchschnittsbeschleunigung berechnen.
Beispielsweise wird bei den technischen Daten von Autos häufig angegeben, wie lange sie benötigen,
um aus der Ruhe auf eine Geschwindigkeit von 100 km/h zu beschleunigen.
Hieraus ergibt sich eine mittlere Beschleunigung, obwohl das Auto zum Ende der Beschleunigungsphase weniger und
während des Schaltens gar nicht beschleunigt wird.
In vielen Fällen beschränken wir uns aber auf konstante Beschleunigungen.
Damit sind Durchschnittsbeschleunigung und Momentanbeschleunigung gleich.
Video 14: Beschleunigung: Beispiel (C)
.
In der folgenden Skizze kann man den Zusammenhang zwischen Weg (blau), Geschwindigkeit (grün) und Beschleunigung (rot) sehen. Die Geschwindigkeit ist die erste, die Beschleunigung die zweite Ableitung des Weges nach der Zeit. Ziehen Sie den blauen Punkt über das Diagramm. Der Massenpunkt bewegt sich zunächst mit großer Geschwindigkeit in positive -Richtung. Diese Bewegung wird stetig abgebremst. Hierfür verantwortlich ist die konstant negative Beschleunigung .
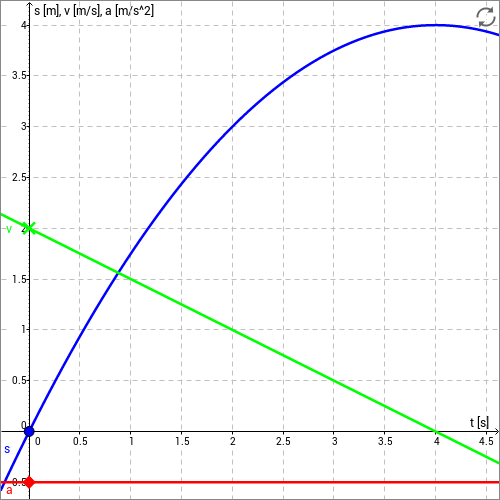
Video 15: Beschleunigung: Beispiel (C)
.
Geschwindigkeit und Beschleunigung im Raum (+)
Video 16: Geschwindigkeit und Beschleunigung im Raum (C)
.
Bislang wurden nur eindimensionale Bewegungen betrachtet. In diesem Fall entspricht eine Beschleunigung der Zu- oder Abnahme der Geschwindigkeit (bei geeigneter Fallunterscheidung evtl. nur des Betrags) entlang einer vorgegebenen Richtung oder Kurve. In zwei oder drei Dimensionen kann jedoch auch die Richtung der Geschwindigkeit geändert werden, denn die Geschwindigkeit ist ja eine vektorielle Größe. Auch wenn die Bewegung eines Körpers seine Richtung ändert, spricht man daher von einer Beschleunigung, selbst wenn der Betrag der Geschwindigkeit konstant bleibt. Letzteres ist z.B. Bei Kreisbewegungen der Fall (siehe Abschnitt 4.5.1 über Kreisbewegungen).
Video 17: Geschwindigkeit und Beschleunigung im Raum: Durchschnittsgeschwindigkeit und -beschleunigung (C)
.
Video 18: Geschwindigkeit und Beschleunigung im Raum: Momentangeschwindigkeit und -beschleunigung (C)
.
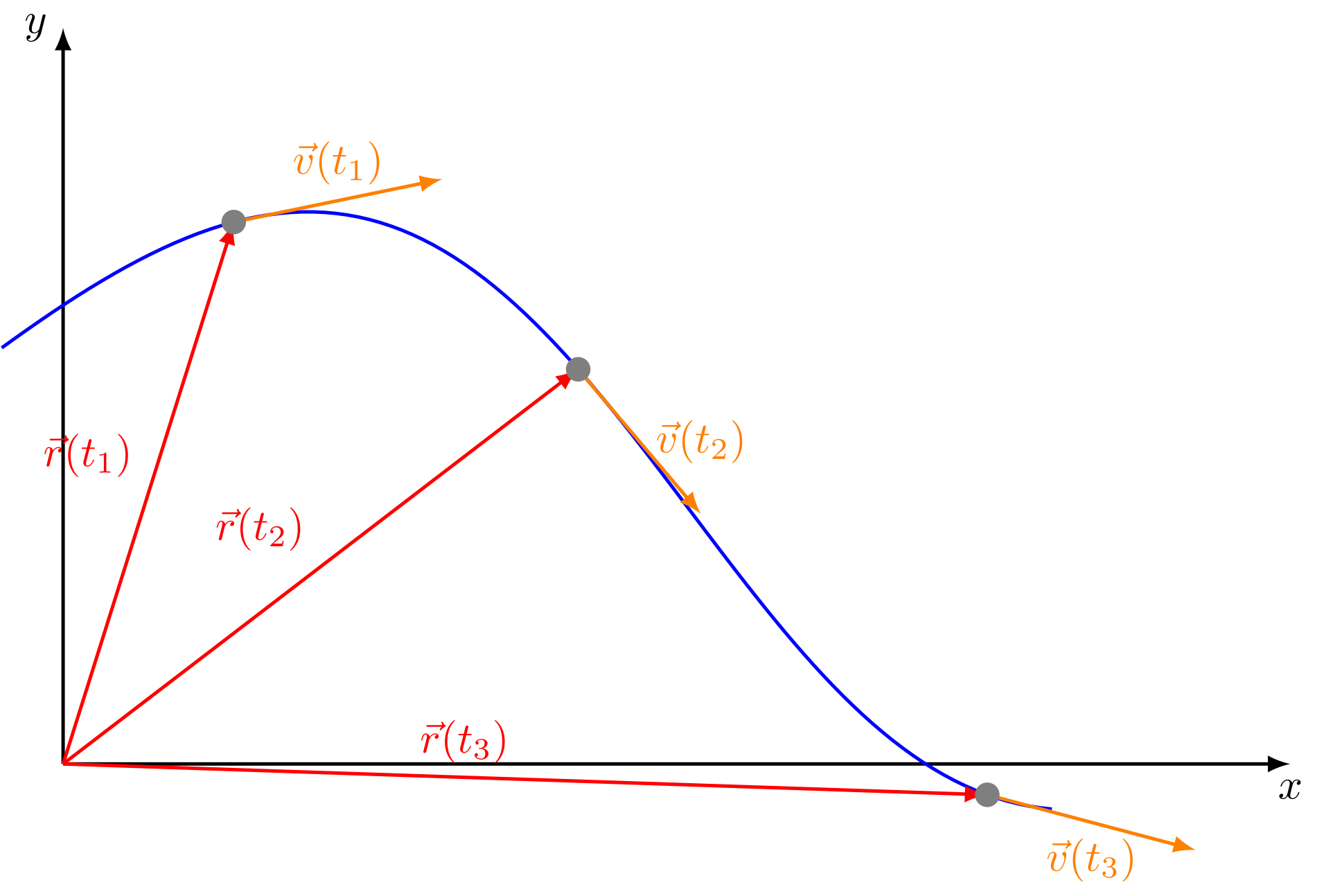
Abbildung 4.2.15: Bewegung in zwei Dimensionen (C)
Um Bewegungen auch im dreidimensionalen Raum zu beschreiben, werden in den obigen Beziehungen die bekannten Variablen Ort, Geschwindigkeit und Beschleunigung als Vektorgrößen dargestellt. Dabei wird aus der Ortsvariablen die Variable , die den sogenannten Ortsvektor darstellt. Man erhält also:
Unter der zeitlichen Ableitung eines Vektors versteht man:
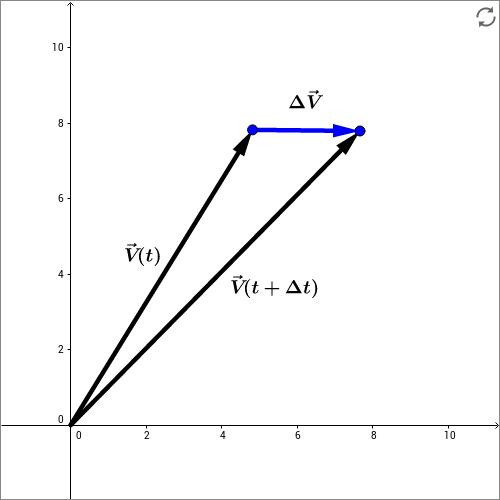
In der folgenden Skizze wird verdeutlicht, dass der Vektor , und damit auch das Differential , nicht nur davon abhängt, wie sich der Betrag von ändert. Entscheidend ist ebenso die Richtungsänderung von im Zeitintervall . Man beachte, dass und damit auch im Allgemeinen nicht in dieselbe Richtung wie zeigen.
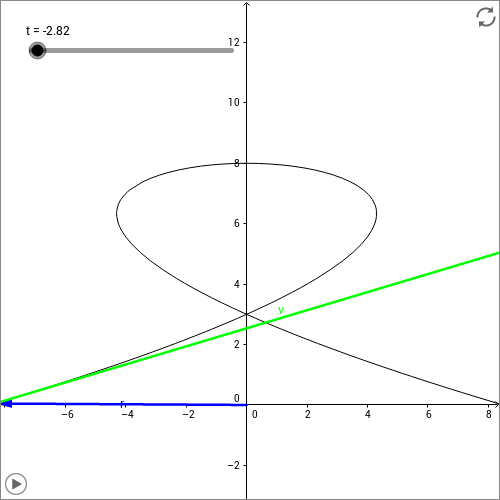
Im folgenden Beispiel ist eine beliebige Bewegung eines Massenpunktes in der zweidimensionalen Ebene dargestellt. Stellen Sie sich z.B. die Bewegung eines Achterbahn-Wagens in einem Looping vor. Der Massenpunkt kommt von links mit einer hohen Geschwindigkeit. Auf der Loopingbahn wird der Massenpunkt zunächst langsamer (abgebremst), anschließend wieder schneller (beschleunigt) und ändert zudem permanent seine Bewegungsrichtung. Alle drei genannten Bewegungsänderungen stellen im physikalischen Sinne eine Beschleunigung des Massenpunktes dar. Das Abbremsen wird hierbei als negative Beschleunigung betrachtet.
In dieser recht komplexen Bewegungskurve ändern sich der Ortsvektor , der Geschwindigkeitsvektor und der Beschleunigungsvektor kontinuierlich. Wie genau diese Änderungen erfolgen, soll hier nicht betrachtet werden. Das Beispiel soll aber illustrieren, dass die drei Vektoren durch die zeitliche Ableitung zwar zusammen hängen, aber dennoch sehr unterschiedliche funktionale Abhängigkeiten von der Zeit besitzen können, sowohl was den Betrag als auch was die Richtung der Größe betrifft. Spielen Sie die Animation ab und beobachten Sie, wie sich die Vektoren , und zeitlich ändern.
Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie .
Falls nicht anders angegeben, verwenden Sie