8.2.4 Doppler-Effekt
Video 3: Akustischer Dopplereffekt: Quelle oder Empfänger bewegt (C)
.
Video 4: Akustischer Dopplereffekt: Quelle UND Empfänger bewegt (C)
.
Video 5: Akustischer Dopplereffekt: Überschall (C)
.
Doppler-Effekt (*)
Herleitung
Annahme: Eine Quelle sendet eine Welle aus, die sich in der Zeit um die Entfernung nach rechts bewegt. In der gleichen Zeit haben sich Quelle und Empfänger um die Entfernungen bzw. bewegt. Jetzt sendet die Quelle eine neue Welle aus.
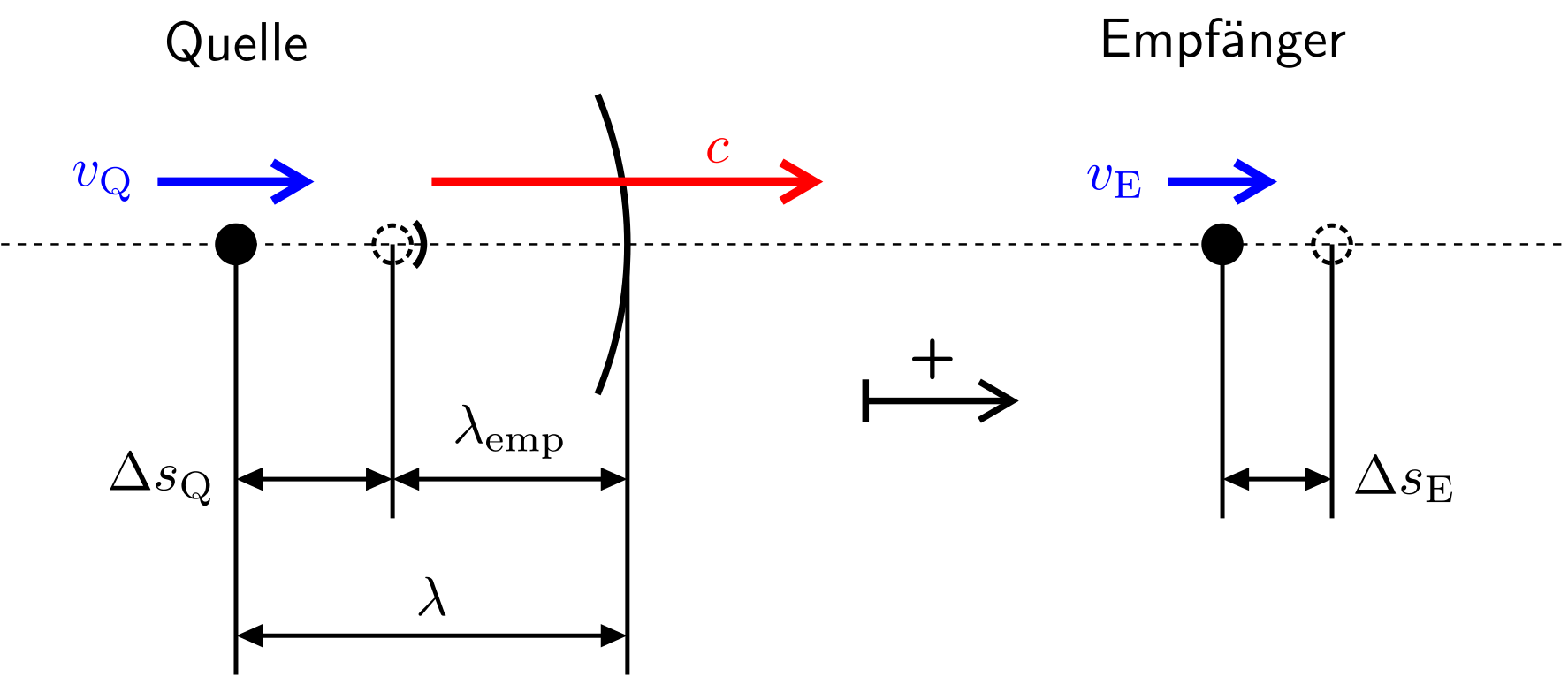
Abbildung 8.2.132: Bewegte Quelle und bewegter Empfänger (C)
Abstand zwischen den Wellenfronten (= empfundene Wellenlänge)
Die Wellenlängen ergeben sich zu
Zu (3): Wenn der Empfänger sich bewegt, empfindet er eine um den Betrag seiner eigenen Geschwindigkeit verringerte Ausbreitungsgeschwindigkeit.
Von der Quelle zurückgelegter Weg
Einsetzen von (2–4) in (1):
Umformen liefert
Doppler-Effekt
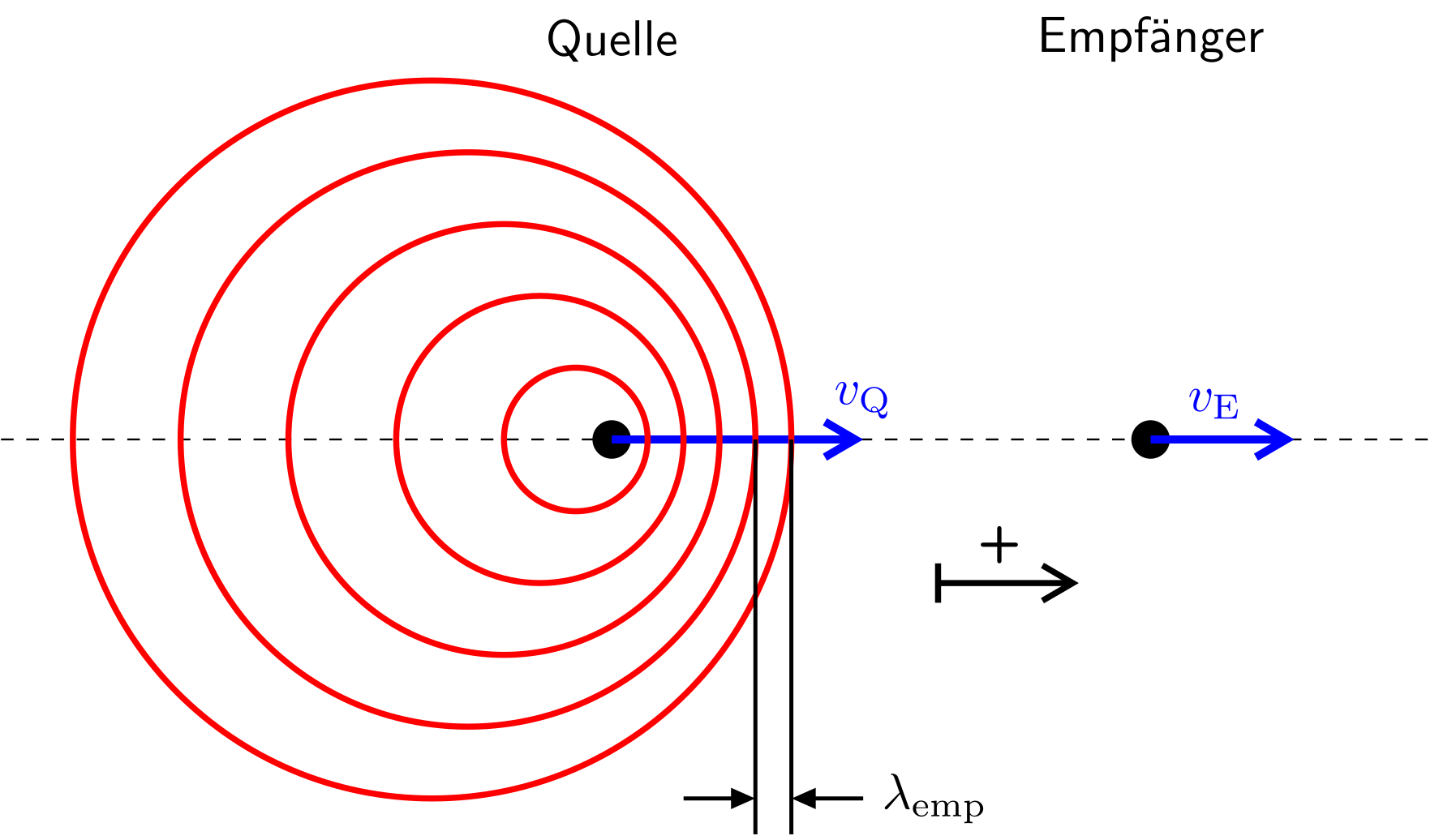
Wenn sich eine Quelle relativ zu einem Empfänger bewegt, nimmt dieser eine höhere oder tiefere Frequenz wahr, als von der Quelle ausgesendet wird.
Auf Grund der Relativbewegung ändert sich die Wellenlänge des Signals. Diese Erscheinung nennt man Doppler-Effekt.
Vom Empfänger wahrgenommene Frequenz
Hinweise
Wenn die Geschwindigkeiten von Quelle und Empfänger aber sehr klein im Vergleich zur Lichtgeschwindigkeit sind, kann eine Näherung verwendet werden, die hier hergeleitet wird:
Mathematischer Hintergrund:
Der mittlere Term ist eine nicht-lineare Funktion (Hyperbel). Es ist eine gängige Praxis, nicht-lineare Funktionen zu linearisieren (durch eine Gerade ersetzen), indem man sie zunächst durch eine „Taylorreihe“ (oder auch Potenzreihe) ausdrückt, die unendlich viele Terme enthält und (für ) gegen die nicht-lineare Funktion konvergiert. Für kleine Werte von können die höheren Potenzen vernachlässigt werden. Man ersetzt also die nicht-lineare Funktion in einem engen Bereich (hier ) durch ihre Tangente. Physikalisch gesehen muss die Geschwindigkeit in diesem Fall also deutlich kleiner als die Lichtgeschwindigkeit sein.
(Hier nimmt man an, dass beide Geschwindigkeiten sehr klein gegenüber sind.)
Bei der Näherung gelten die gleichen Vorzeichenregelungen wie in den Hinweisen weiter oben beschrieben, d.h. wenn sich der Empfänger z.B. auf die Quelle zubewegt, muss „“ für „“ eingesetzt werden (und dann ist ). Gleiches gilt für die Quelle, wenn sie sich vom Empfänger wegbewegt.
Technische Anwendungen
Laser-Doppler-Anemometer (Geschwindigkeitsmessung), Ultraschalldiagnostik, uvm.
Wenn sich eine Quelle relativ zu einem Empfänger bewegt, nimmt dieser eine höhere oder tiefere Frequenz wahr, als von der Quelle ausgesendet wird.
Auf Grund der Relativbewegung ändert sich die Wellenlänge des Signals. Diese Erscheinung nennt man Doppler-Effekt.

Abbildung 8.2.133: Doppler-Effekt (C)
Vom Empfänger wahrgenommene Frequenz
Hinweise
- Vorzeichenregelung: Pos. Vorzeichen immer in Ausbreitungsrichtung der Wellen zum Empfänger. Die Vorzeichen von werden dann relativ dazu definiert.
- Wenn sich das Medium nicht in Ruhe befindet (z.B. bei Wind im Medium Luft), ist die Ausbreitungsgeschwindigkeit durch zu ersetzen.
- Gl. (8.2.1) gilt nur für . Würde sich z.B. eine Schallquelle mit Schallgeschwindigkeit bewegen, wäre die empfundene Wellenlänge Null (vgl. „Schallmauer“).
Wenn die Geschwindigkeiten von Quelle und Empfänger aber sehr klein im Vergleich zur Lichtgeschwindigkeit sind, kann eine Näherung verwendet werden, die hier hergeleitet wird:
| Umformung von Gl. (8.2.1) | |
| Annäherung des mittleren Terms durch eine Taylorreihe (mit ): |
Der mittlere Term ist eine nicht-lineare Funktion (Hyperbel). Es ist eine gängige Praxis, nicht-lineare Funktionen zu linearisieren (durch eine Gerade ersetzen), indem man sie zunächst durch eine „Taylorreihe“ (oder auch Potenzreihe) ausdrückt, die unendlich viele Terme enthält und (für ) gegen die nicht-lineare Funktion konvergiert. Für kleine Werte von können die höheren Potenzen vernachlässigt werden. Man ersetzt also die nicht-lineare Funktion in einem engen Bereich (hier ) durch ihre Tangente. Physikalisch gesehen muss die Geschwindigkeit in diesem Fall also deutlich kleiner als die Lichtgeschwindigkeit sein.
| mit | |
| Ausmultiplizieren der Klammer: | |
| mit und |
| Umformen liefert die Näherung |
Näherung für elektromagnetische Wellen
Vom Empfänger wahrgenommene Frequenz
Vom Empfänger wahrgenommene Frequenz
| mit | Relativgeschwindigkeit zw. Quelle und Empfänger | |
| Vom Empfänger wahrgenommene Frequenzerhöhung |
Technische Anwendungen
Laser-Doppler-Anemometer (Geschwindigkeitsmessung), Ultraschalldiagnostik, uvm.
Beispiel
8.2.7
Sie werden in einer 30er Zone bei einer Polizeikontrolle geblitzt. Das Radargerät sendet bei der Bestimmung der Geschwindigkeit elektromagnetische Wellen mit der Frequenz aus. Die Radarwellen laufen zum Auto, werden dort reflektiert, und das Radargerät misst einen Frequenzunterschied zwischen gesendeter und empfangener Frequenz von . Sie wissen, dass ab einer Geschwindigkeitsüberschreitung von ein Fahrverbot ausgesprochen wird. Müssen Sie bald Fahrrad fahren?
Sie werden in einer 30er Zone bei einer Polizeikontrolle geblitzt. Das Radargerät sendet bei der Bestimmung der Geschwindigkeit elektromagnetische Wellen mit der Frequenz aus. Die Radarwellen laufen zum Auto, werden dort reflektiert, und das Radargerät misst einen Frequenzunterschied zwischen gesendeter und empfangener Frequenz von . Sie wissen, dass ab einer Geschwindigkeitsüberschreitung von ein Fahrverbot ausgesprochen wird. Müssen Sie bald Fahrrad fahren?



