2. Mechanik
  3. Drehbewegungen
  4. Bewegungsgesetz (*),(+)

4.5.2 Bewegungsgesetz der Rotation und Drehimpulserhaltung





 

Noch kein Basiswissen vorhanden ...
Zu diesem Abschnitt gibt es leider noch kein Basiswissen.

Dieses Thema wird in der Schule meist nicht behandelt. Die folgende kurze Zusammenfassung kann aber dennoch eine nützliche Vorbereitung auf die Behandlung des Themas im Studium darstellen. 
 


Video 22: Das Bewegungsgesetz der Rotation (C) .



 

Das Bewegungsgesetz der Rotation (*)
Das Bewegungsgesetz der Rotation kann man herleiten, indem man auf das Bewegungsgesetz des 2. newtonschen Axioms von links das Kreuzprodukt mit r → anwendet:

F → = d p → dt ⇒  r → × F → = r → × d p → dt  .

Andererseits gilt: Bei der Ableitung eines Vektorprodukts wendet man wie bei einem normalen Produkt zweier Funktionen die Produktregel an:
 
d dt ( r → × p → )  ​ = d r → dt × p → + r → × d p → dt   ​ = v → ×m v → + r → × d p → dt   ​ = r → × d p → dt  ,
 
weil v → × v → =0. D.h. obiges Bewegungsgesetz kann auch geschrieben werden als

r → × F → = d dt ( r → × p → ) .

 

Nun führt man zwei neue physikalische Größen ein: 
Das Drehmoment M → haben wir beim Hebelgesetz bereits definiert.  
Drehmoment = Kraft mal Hebelarm oder M=| F → |·| r → |·sinφ, φ=​ Winkel zwischen F → und r → .  
Vektoriell wird dieser Zusammenhang ausgedrückt durch das Kreuzprodukt

M → = r → × F →  .

Des Weiteren definiert man den Drehimpuls L → gemäß

L → = r → × p →  .

Daraus erhält man das Bewegungsgesetz der Rotation:

M → = d L → dt  .

Video 23: Drehmoment und Drehimpuls (C) .

 

Das Drehmoment (+)
Der Vektor des Drehmoments M → steht senkrecht auf den beiden Vektoren r → und F → . Für die Orientierung gilt die Rechte-Hand-Regel:  

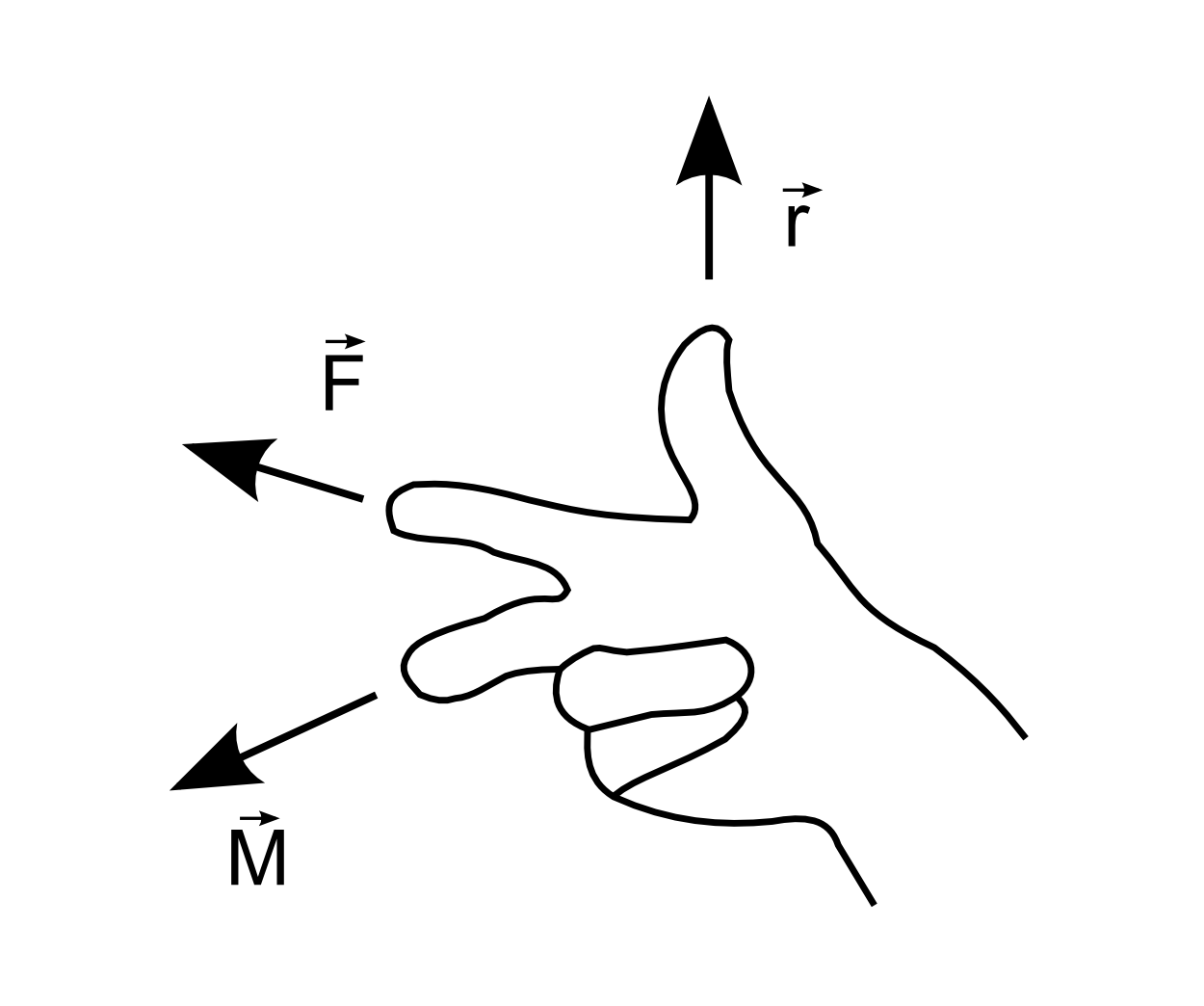
././Physikkurs/drehbewegung_gesetzedrehimpuls/images/MFILE3xRechte-Hand-Regel-2.png
Abbildung 4.5.59: Rechte-Hand-Regel (C)




Wie oben erläutert, erhält man den Betrag des Drehmoments wie folgt:

M=rF sinφ ,

wobei φ der Winkel zwischen den beiden Vektoren r → und F → ist. 
Die Einheit des Drehmoments ist das Newtonmeter:

1 N m=1  kg  m2 s2    (≠1 J  ! ) .

Das Newtonmeter ist zwar das gleiche Produkt aus SI-Basiseinheiten wie das Joule. Es handelt sich bei dem Drehmoment und der Energie jedoch um völlig unterschiedliche physikalische Größen. Daher darf man das Drehmoment nicht in Einheiten von Joule angeben.

In der folgenden Skizze wird die Bildung des Drehmoments veranschaulicht. Die beiden Vektoren r → und F → liegen in der (x,y)-Ebene. Diese Ebene ist in der oberen Hälfte der Skizze gezeigt. Darunter dargestellt ist die (z,y)-Ebene, wobei man in Richtung der x-Achse schaut. Das erzeugte Drehmoment M → steht senkrecht auf r → und F → und damit parallel zur z-Achse. 
Verändern Sie den Kraftvektor F → bzw. den Ortsvektor r → und beobachten Sie, wie sich das Drehmoment M → ändert. Wann zeigt M → in, wann entgegen der z-Richtung? Wann verschwindet das Drehmoment?  

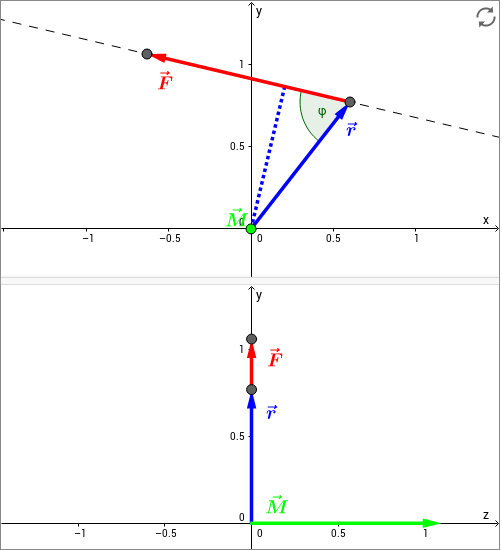
././Physikkurs/drehbewegung_gesetzedrehimpuls/images/geogebra_drehbewegung_standbild3.png
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)

In der obigen Skizze ist zusätzlich noch die Komponente r⊥ des Ortsvektors r → senkrecht zur angreifenden Kraft F → gestrichelt eingezeichnet. Da diese Komponente die Gegenkathete zu φ in einem rechtwinkligen Dreieck ist, beträgt ihre Länge:

r⊥ =rsinφ .

Damit kann der Betrag des Drehmoments auch berechnet werden zu

M= r⊥ F .

Die Strecke r⊥ ist der kleinste Abstand zwischen der Drehachse und einer Geraden, die durch den Angriffspunkt der Kraft in Kraftrichtung verläuft. Dieser Abstand wird auch als effektiver Hebelarm bezeichnet.  

Der Drehimpuls (*)
Ganz allgemein ist für Massenpunkte m, die sich am Ort r → mit der Geschwindigkeit v → bewegen, der Drehimpuls definiert als:

L → = r → × p → =m  r → × v →  .

Eine häufige Anwendung ist jedoch der Fall, dass der Massenpunkt eine Kreisbewegung ausführt und man den Drehimpuls bezüglich des Kreismittelpunktes berechnen will. Hier stehen Geschwindigkeitsvektor v → und Ortsvektor r → senkrecht aufeinander. Die Formel für den Betrag des Drehimpulses vereinfacht sich dadurch zu

L=mrv .

Nach dem Bewegungsgesetz der Rotation gilt:

M → = d L → dt  .

Daraus folgt, dass sich der Drehimpuls nur dann ändert, wenn ein Drehmoment wirkt. Dies ist eine Erweiterung des 1. newtonschen Axioms. Ebenso wie der Impuls bleibt auch der Drehimpuls L → in abgeschlossenen Systemen erhalten. Es gilt der Drehimpulserhaltungssatz:

M → = 0 →  ↔  L → = const  .

Man sagt dann auch, der Drehimpuls sei eine Konstante der Bewegung.  



Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie g=9,81  m s2  .