5.3.4 Spulen
Video 9: Parallel- und Reihenschaltung von Spulen (C)
.
Auch die Spule haben wir schon kennengelernt (Seiten 5.2.4 und 5.2.5).
Sie ist ein Leiter mit Selbstinduktion. Der Änderung einer sie durchfließenden Stromstärke setzt sie eine Induktionsspannung entgegen. Dieses Vermögen der Erzeugung einer Gegenspannung nennt man ihre Induktivität . Es ist:
Hiermit ist die Spule relevant, wenn sich der Strom ändert, zum Beispiel bei Ein- und Ausschaltvorgängen sowie bei Wechselspannungen. Im Fall einer Gleichspannung hat die ideale Spule (verschwindender ohmscher Widerstand) keinen Einfluss auf den Stromkreis. Die Einheit der Induktivität ist das Henry (). Das Schaltzeichen der Spule ist:

Reihenschaltung (+)
In der folgenden Skizze ist die Reihenschaltung von mehreren Spulen dargestellt.
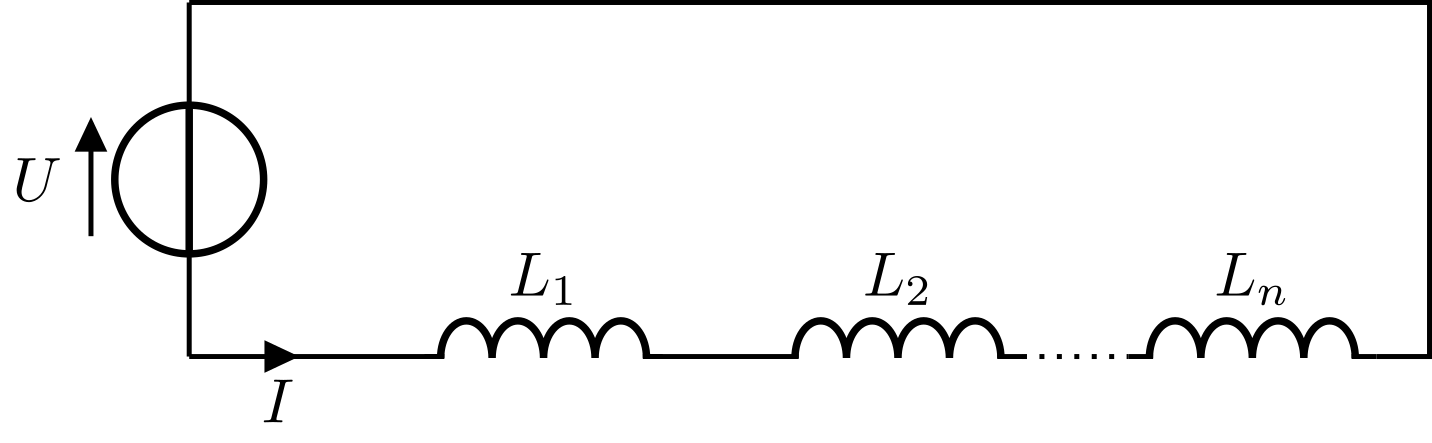
Bei der Reihenschaltung befinden sich alle Spulen in einer gemeinsamen Masche. Darüber hinaus werden sie alle von der gleichen Stromstärke durchflossen. Wird zu einem Zeitpunkt schlagartig eine konstante Spannung an die Schaltung angelegt, erzeugt dies eine zeitliche Änderung des Gesamtstroms , und in jeder Einzelspule wird gemäß dem Induktionsgesetz die Spannung erzeugt. Die Maschenregel besagt, dass die Summe der Induktionsspannungen an den Einzelspulen gerade gleich der Spannung der Spannungsquelle sein muss:
Damit ergibt sich als Gesamtinduktivität :
Parallelschaltung (+)
Die folgende Skizze zeigt die Parallelschaltung von Spulen.
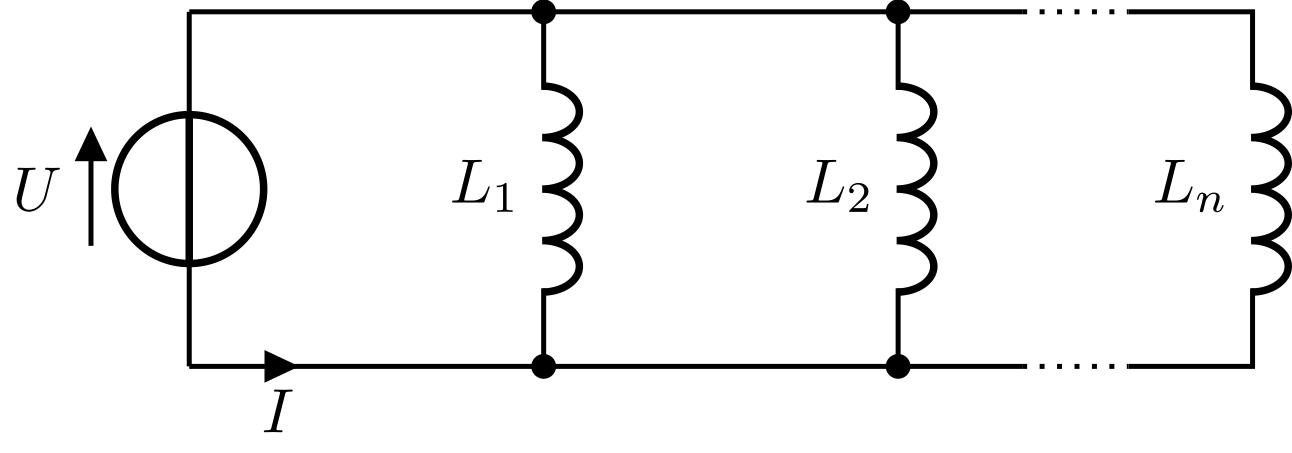
Bei der Parallelschaltung liegt an allen Spulen die gleiche Spannung an. Wird zu einem Zeitpunkt schlagartig eine konstante Spannung an die Schaltung angelegt, so wird in jeder Einzelspule abhängig von der Induktivität eine Stromänderung verursacht:
Damit ergibt sich für die Gesamtinduktivität :
Hiermit ist die Spule relevant, wenn sich der Strom ändert, zum Beispiel bei Ein- und Ausschaltvorgängen sowie bei Wechselspannungen. Im Fall einer Gleichspannung hat die ideale Spule (verschwindender ohmscher Widerstand) keinen Einfluss auf den Stromkreis. Die Einheit der Induktivität ist das Henry (). Das Schaltzeichen der Spule ist:

Abbildung 5.3.116: Schaltzeichen einer Spule (C)
Reihenschaltung (+)
In der folgenden Skizze ist die Reihenschaltung von mehreren Spulen dargestellt.

Abbildung 5.3.117: Reihenschaltung von Spulen (C)
Bei der Reihenschaltung befinden sich alle Spulen in einer gemeinsamen Masche. Darüber hinaus werden sie alle von der gleichen Stromstärke durchflossen. Wird zu einem Zeitpunkt schlagartig eine konstante Spannung an die Schaltung angelegt, erzeugt dies eine zeitliche Änderung des Gesamtstroms , und in jeder Einzelspule wird gemäß dem Induktionsgesetz die Spannung erzeugt. Die Maschenregel besagt, dass die Summe der Induktionsspannungen an den Einzelspulen gerade gleich der Spannung der Spannungsquelle sein muss:
Damit ergibt sich als Gesamtinduktivität :
Die Gesamtinduktivität einer Reihenschaltung von Spulen ist gleich der Summe der Einzelinduktivitäten:
Beispiel
5.3.20
Drei -Spulen werden in Reihe geschaltet.
Bei der Reihenschaltung von Spulen ergibt sich die Gesamtinduktivität als Summe der Einzelinduktivitäten. Damit gilt für :
Die Gesamtinduktivität der Schaltung beträgt also .
Drei -Spulen werden in Reihe geschaltet.
Bei der Reihenschaltung von Spulen ergibt sich die Gesamtinduktivität als Summe der Einzelinduktivitäten. Damit gilt für :
Die Gesamtinduktivität der Schaltung beträgt also .
Parallelschaltung (+)
Die folgende Skizze zeigt die Parallelschaltung von Spulen.

Abbildung 5.3.118: Parallelschaltung von Spulen (C)
Bei der Parallelschaltung liegt an allen Spulen die gleiche Spannung an. Wird zu einem Zeitpunkt schlagartig eine konstante Spannung an die Schaltung angelegt, so wird in jeder Einzelspule abhängig von der Induktivität eine Stromänderung verursacht:
Damit ergibt sich für die Gesamtinduktivität :
Der Kehrwert der Gesamtinduktivität einer Parallelschaltung von Spulen ist gleich der Summe der Kehrwerte der Einzelinduktivitäten:
Beispiel
5.3.21
Zwei -Spulen werden parallel geschaltet.
Bei der Parallelschaltung von Spulen ist der Kehrwert der Gesamtinduktivität gegeben als Summe der Kehrwerte der Einzelinduktivitäten. Mit gilt hier
Schließlich muss davon noch der Kehrwert gebildet werden und mal erhält
Der Gesamtinduktivität der Schaltung beträgt .
Zwei -Spulen werden parallel geschaltet.
Bei der Parallelschaltung von Spulen ist der Kehrwert der Gesamtinduktivität gegeben als Summe der Kehrwerte der Einzelinduktivitäten. Mit gilt hier
Schließlich muss davon noch der Kehrwert gebildet werden und mal erhält
Der Gesamtinduktivität der Schaltung beträgt .
Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.

