2. Elektromagnetismus
  3. Strom und Magnetismus
  4. Elektromagnetische Induktion (+)

5.2.4 Elektromagnetische Induktion





 

Noch kein Basiswissen vorhanden ...
Zu diesem Abschnitt gibt es leider noch kein Basiswissen.

Video 14: Elektromagnetische Induktion (C) .



Video 15: Elektromagnetische Induktion: Theorie (C) .



 

Der magnetische Fluss (+)


Unter dem magnetischen Fluss versteht man das über eine gegebene Fläche integrierte B-Feld. Im Prinzip „zählt“ man die Feldlinien, die die Fläche durchdringen. Durchdringen die Magnetfeldlinien die Fläche senkrecht, so erhält man für den magnetischen Fluss Φ:

Φ=B·A .

Betrachtet man eine Fläche A=b·l, die unter einem Winkel φ im Magnetfeld liegt (genauer: deren Normalenvektor den Winkel φ mit dem magnetischen Feld B → einschließt), so wird effektiv nur die auf die Waagrechte projizierte Fläche A' =bcosφ·l von den Feldlinien durchdrungen. Man kann auch sagen: Es trägt nur die auf der Fläche A senkrechte Komponente des B-Felds zum magnetischen Fluss bei:
Magnetischer Fluss  


Φ=B A cosφ .

Vektoriell ausgedrückt wird es durch das Skalarprodukt:

Φ= B → · A →  .



Dies wird für die Fläche einer rechteckigen Leiterschleife in einem homogenen Magnetfeld in der folgenden Abbildung illustriert:

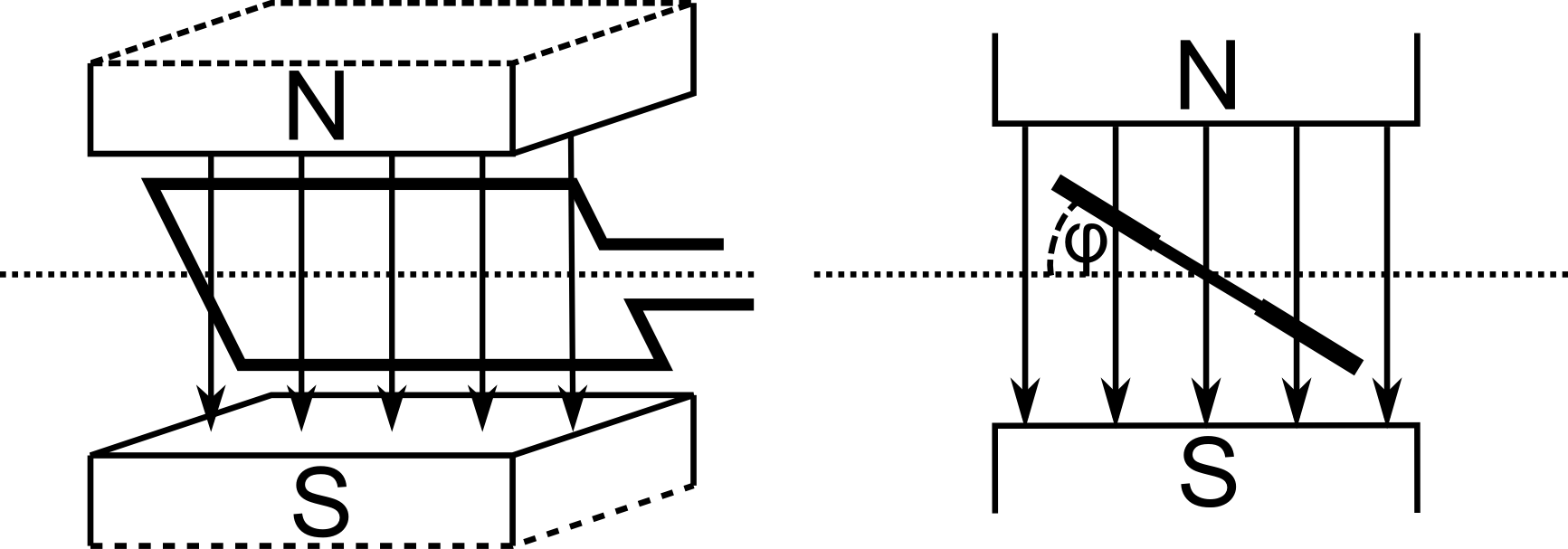
././Physikkurs/strommagnetisch_induktion/images/MFILE4xWechselstromgenerator.png
Abbildung 5.2.95: Leiterschleife in homogenem Magnetfeld (C)



 

Das Induktionsgesetz (+)


Ändert sich zeitlich der magnetische Fluss Φ durch eine Leiterschleife mit der Fläche A, so kann man zwischen den beiden Enden der Leiterschleife eine Spannung messen: es wird eine Spannung induziert. Dabei kann die Veränderung des magnetischen Flusses auf drei Arten erfolgen:  

  • eine Änderung der Stärke des Magnetfelds B;

  • eine Änderung der Fläche A;

  • eine geänderte Orientierung der Fläche A relativ zum Magnetfeld B → .



Dieses Phänomen hat Faraday in seinem Induktionsgesetz beschrieben:
Induktionsgesetz  


U ind =- dΦ dt =- d( B → · A → ) dt =- d(A B cosφ) dt  .



Handelt es sich nicht um eine Leiterschleife, sondern um eine Spule mit N hintereinander liegenden Schleifen der gleichen Fläche, so ist die induzierte Spannung auch N-mal so groß:

U=-N dΦ dt  .

Schließt man die Leiterschleife kurz, fließt aufgrund der induzierten Spannung ein Strom. Dieser Strom erzeugt wiederum ein Magnetfeld, das das äußere Magnetfeld schwächt, also seiner Ursache entgegenwirkt. Würde das Magnetfeld das äußeren Magnetfeld verstärken, gäbe es eine ständig wachsende Induktionsspannung. Dies widerspricht der Energieerhaltung.
Die Lenzsche Regel  
Die Induktionsspannung ist so gerichtet, dass die dadurch entstehenden Induktionsströme der Ursache der Induktion entgegenstehen.


Die Lenzsche Regel drückt man durch das Minuszeichen bei der Induktionsspannung aus.

Beispiel 5.2.26  
Bewegt man einen leitfähigen Draht senkrecht zu einem homogenen Magnetfeld, sind das bewegte Elektronen in einem Magnetfeld: die Elektronen erfahren eine Lorentz-Kraft senkrecht zur Bewegungsrichtung und senkrecht zum Magnetfeld:

F L =e·B·v .

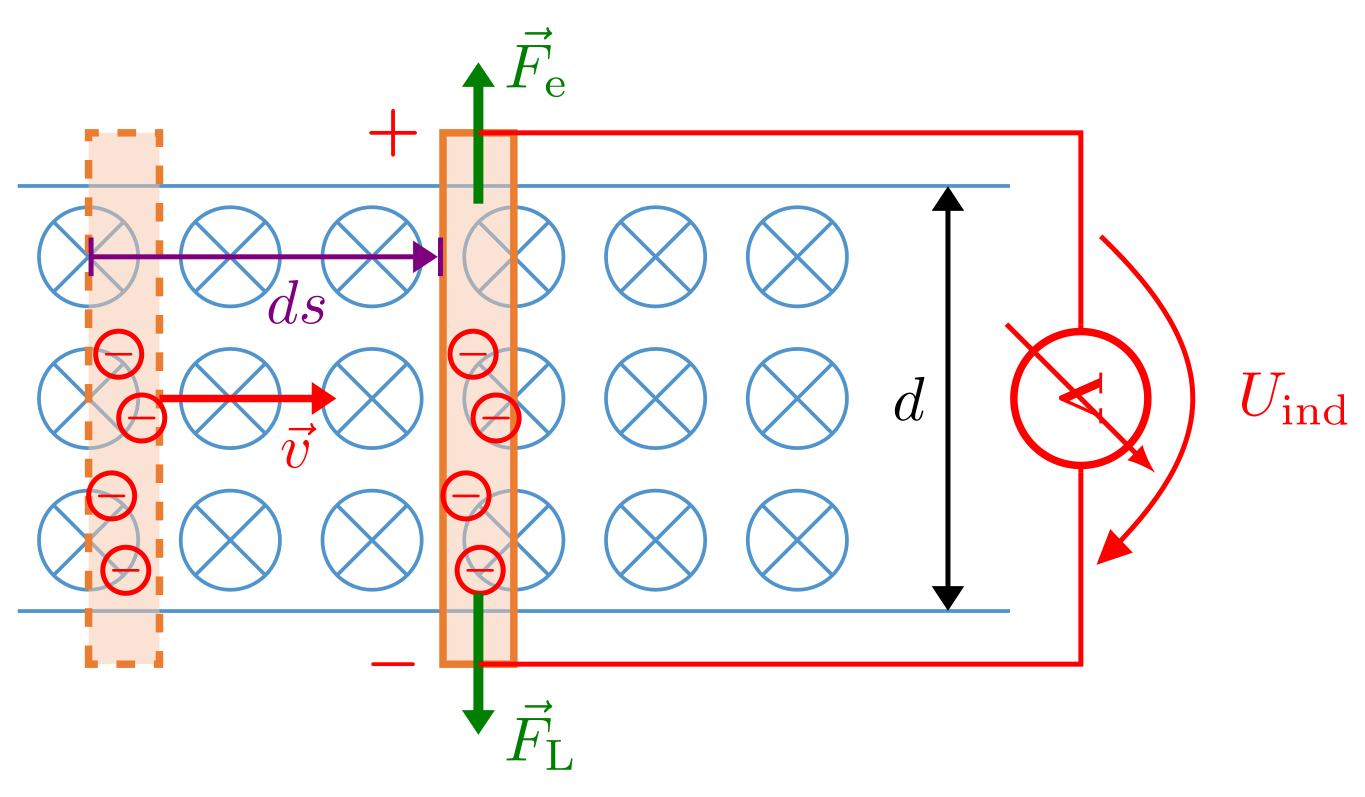
./_C2CB4674_4x.png
Abbildung 5.2.96: Bewegung eines Drahtes im Magnetfeld  (C)



Dadurch entsteht an dem einen Ende des Leiters ein Elektronenüberschuss, am anderen Ende ein Elektronenmangel. Es bildet sich zwischen den beiden Enden ein elektrisches Feld aus und man misst eine Spannung, die Induktionsspannung

U ind =E·d .

Durch das elektrische Feld E wirkt wiederum eine Kraft auf die Elektronen, die der Lorentz-Kraft entgegengesetzt ist:

F C =e·E=e· U ind d  .

Zwischen beiden Kräften bildet sich ein Gleichgewicht aus:

e·B·v=e· U ind d  .

Lösen wir diese Gleichung nach U ind auf und setzen an dieser Stelle die Definition der Geschwindigkeit ein, erhalten wir

U ind =B·v·d=B· ds dt ·d .

Im Bild sehen wir, dass sich bei der Bewegung des Leiters um die Länge ds die vom Magnetfeld durchdrungene Fläche um dA=d·ds geändert hat. Damit wird die induzierte Spannung

U ind =B· dA dt  .

Dieses Ergebnis hätten wir auch erhalten, wenn wir das Induktionsgesetz direkt verwendet hätten und dabei berücksichtigen, dass das Magnetfeld konstant ist und die Bewegung des Leiters senkrecht zum Magnetfeld erfolgt ( φ=0, cosφ=1):

U ind = dΦ dt =B· dA dt  .



Beispiel 5.2.27  
Nun betrachten wir anstelle des endlichen Leiters eine Leiterschleife und bewegen diese durch das Magnetfeld.

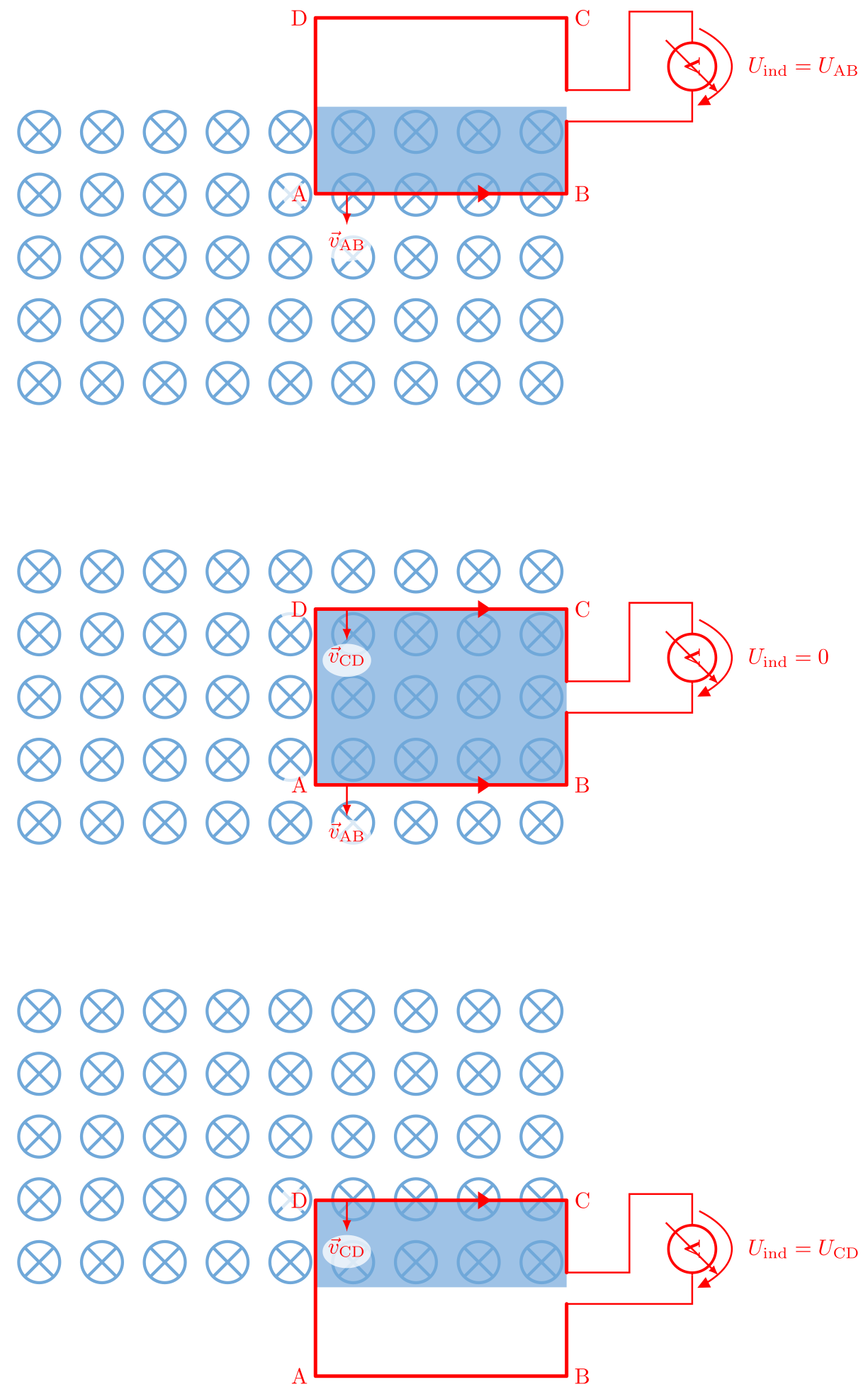
./_42D5557A_4x.png
Abbildung 5.2.97: Bewegung einer Leiterschleife durch ein Magnetfeld  (C)



  • Beim Eintauchen der Fläche in das Magnetfeld wird die vom Magnetfeld durchsetzte Fläche immer größer, die zeitliche Änderung der durchsetzten Fläche ist positiv. Es wird eine Induktionsspannung gemessen.

  • Befindet sich die gesamte Fläche im Magnetfeld, bleibt die vom Magnetfeld durchsetzte Fläche konstant, es gibt keine zeitliche Änderung und damit keine Induktionsspannung.

  • Erst wenn die Leiterschleife aus dem Magnetfeld austritt, wird die durchsetzte Fläche kleiner, die zeitliche Änderung der durchsetzten Fläche ist negativ. Es kann wieder eine Spannung nachgewiesen werden, die jetzt das umgekehrte Vorzeichen hat.





Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Verwenden Sie e=1,602 · 10-19   C und μ0 =4π · 10-7   T m A  .