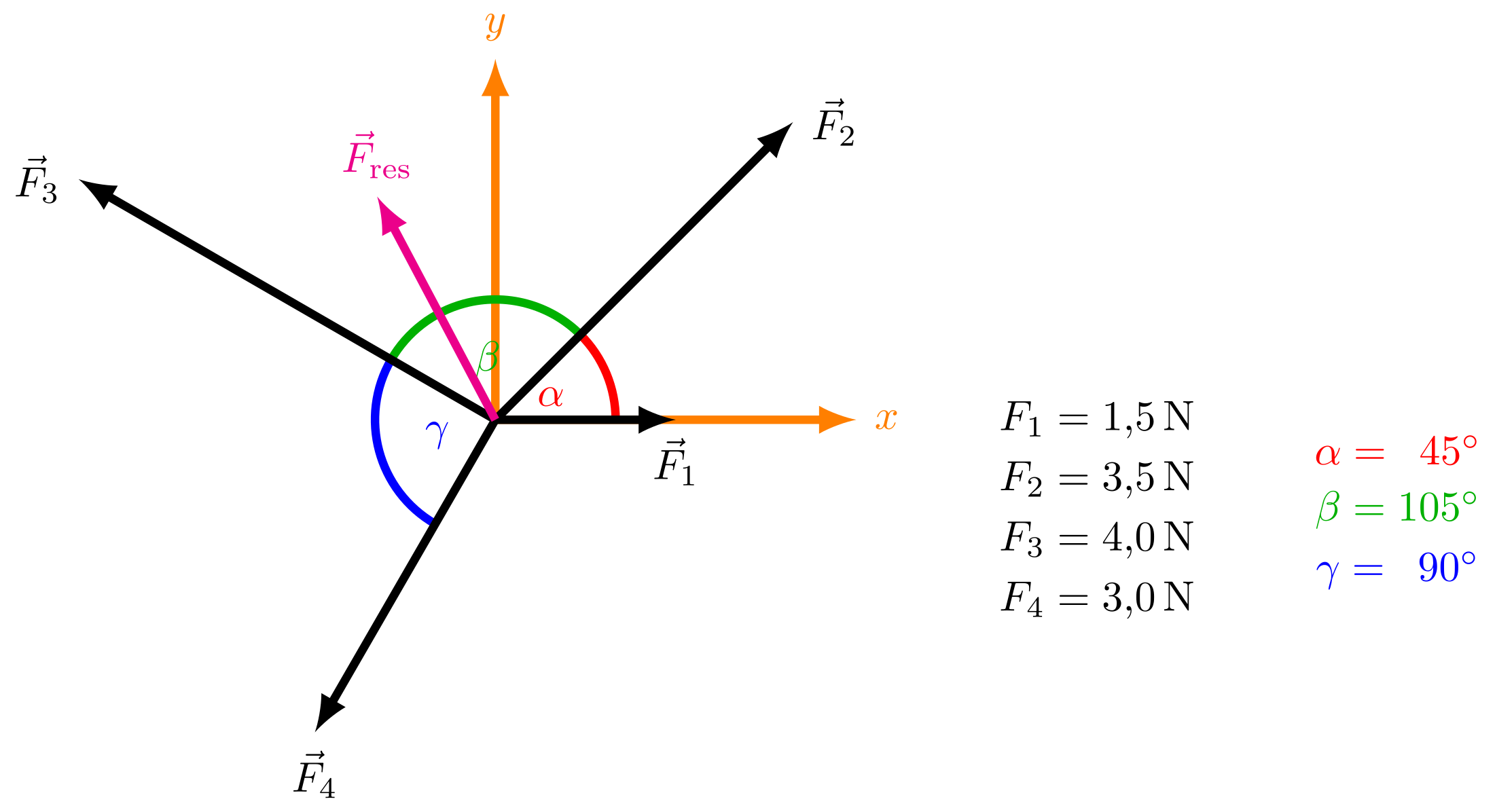4.1.3 Kräftezerlegung
Auf dieser Seite werden die trigonometrischen Funktionen Sinus, Kosinus und Tangens verwendet. Diese werden z.B. im Onlinekurs Mathematik, Kapitel 6.5 behandelt.
Basiswissen „Koordinatensysteme“
Die Position eines Punktes oder Körpers im Raum ist unabhängig vom Betrachter. Allerdings ist die Ortsangabe eines Körper davon abhängig, wo sich der Betrachter befindet. Um die Position eines Körpers im Raum beschreiben zu können, werden deshalb sogenannte Koordinatensysteme eingeführt. Damit können Positionen von Körpern aller Art beschrieben werden. Bekannte Systeme stellen zum Beispiel die Himmelsrichtungen oder auch die Längen- und Breitengrade dar.
Die Lage der Hochschule Reutlingen kann dann auf verschiedene Weise beschrieben werden:
- südlich von Stuttgart
- in Dezimalgrad N und O
- in Grad, Minuten und Sekunden N und O
Was kennzeichnet ein Koordinatensystem? In der Abbildung sind zwei Koordinatensysteme gezeigt. Dabei wird ein Punkt im Raum als Ursprung gewählt und als Nullpunkt gesetzt. Zusätzlich werden drei Raumrichtungen , und definiert und durch Achsen gekennzeichnet, die sich im Ursprung schneiden. Sie heißen Koordinatenachsen. Versieht man sie mit einem Maßstab, kann jeder beliebige Punkt im Raum mit Hilfe dieses Systems beschrieben werden. Bei den in der Abbildung gezeigten Systemen handelt es sich um kartesische Koordinatensysteme. Das bedeutet, dass die Koordinatenachsen jeweils senkrecht aufeinander stehen.
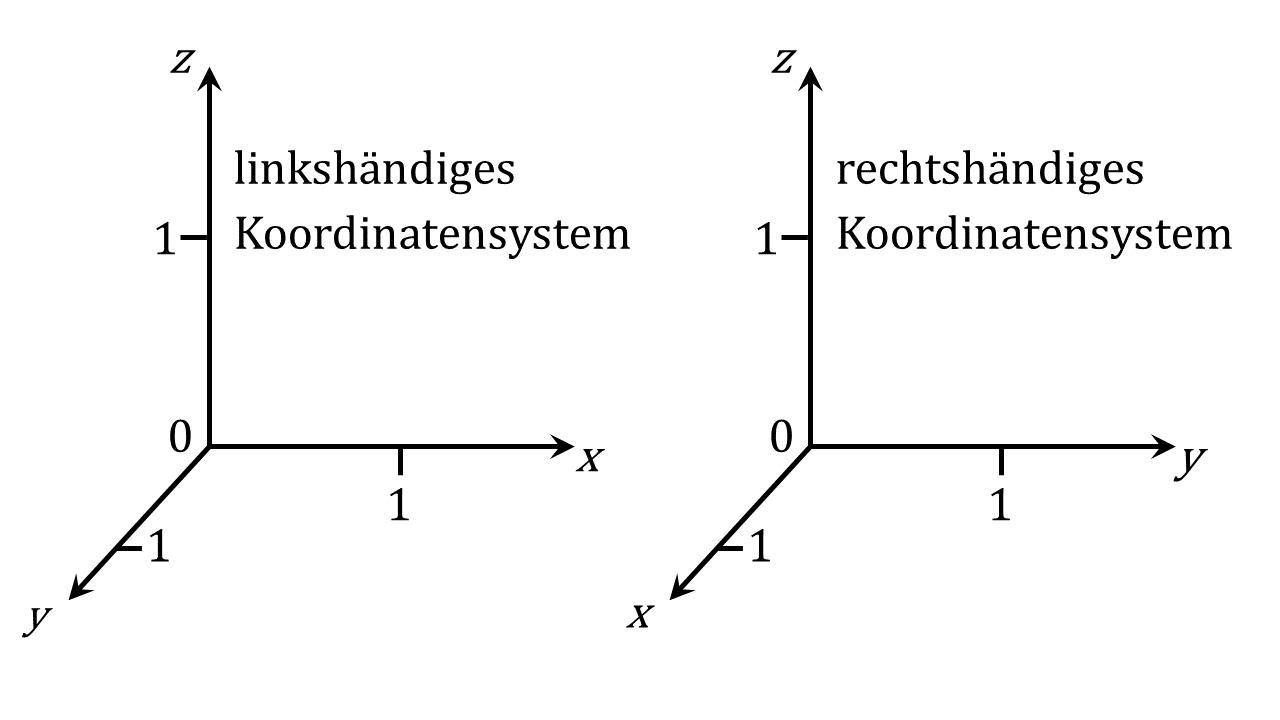
Abbildung 4.1.107: Darstellung eines kartesischen Koordinatensystems (C)
Der Unterschied zwischen den beiden gezeigten Koordinatensystemen ist ihre sogenannte Händigkeit. Versucht man, seine rechte Hand so zu drehen, dass der Daumen in -Richtung, der Zeigefinger in -Richtung und der Mittelfinger in -Richtung zeigt, ist das beim rechten Koordinatensystem möglich. Man spricht von einem rechtshändigen Koordinatensystem. Für das linke Koordinatensystem klappt obiges Vorgehen nur mit der linken Hand, man spricht von einem linkshändigen System. Üblicherweise wird in Naturwissenschaft und Technik überwiegend mit rechtshändigen Koordinatensystemen gearbeitet.
Beispiel
4.1.25
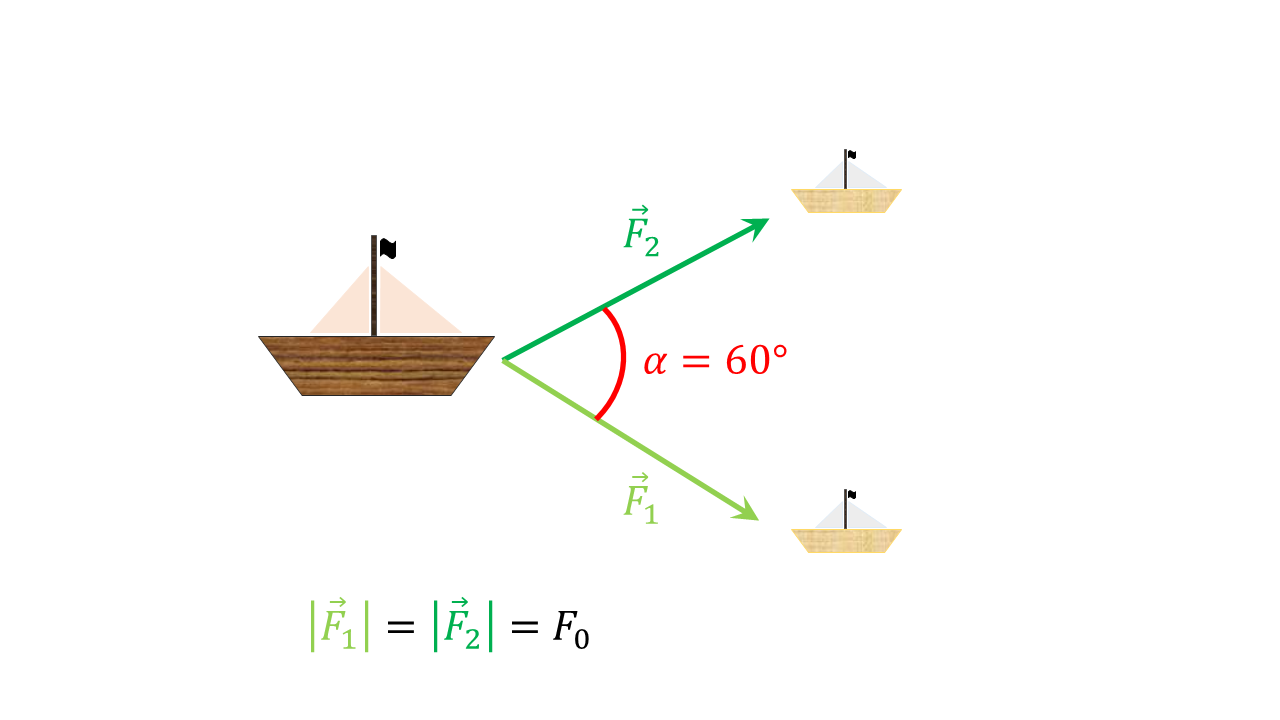
Ein großes Schiff wird von zwei Schleppern mit Hilfe von Trossen in den Hafen gezogen. Der Winkel zwischen den beiden gleich langen Drahtseilen beträgt . Die Kräfte in den Trossen haben den gleichen Betrag. In der Abbildung ist die Situation skizziert.
Welches Koordinatensystem ist geeignet zur Beschreibung der Situation und damit zur Lösung eines Problems? Es sollen im Folgenden zwei mögliche Koordinatensysteme betrachtet und die resultierende Kraft und ihr Betrag allgemein berechnet werden.
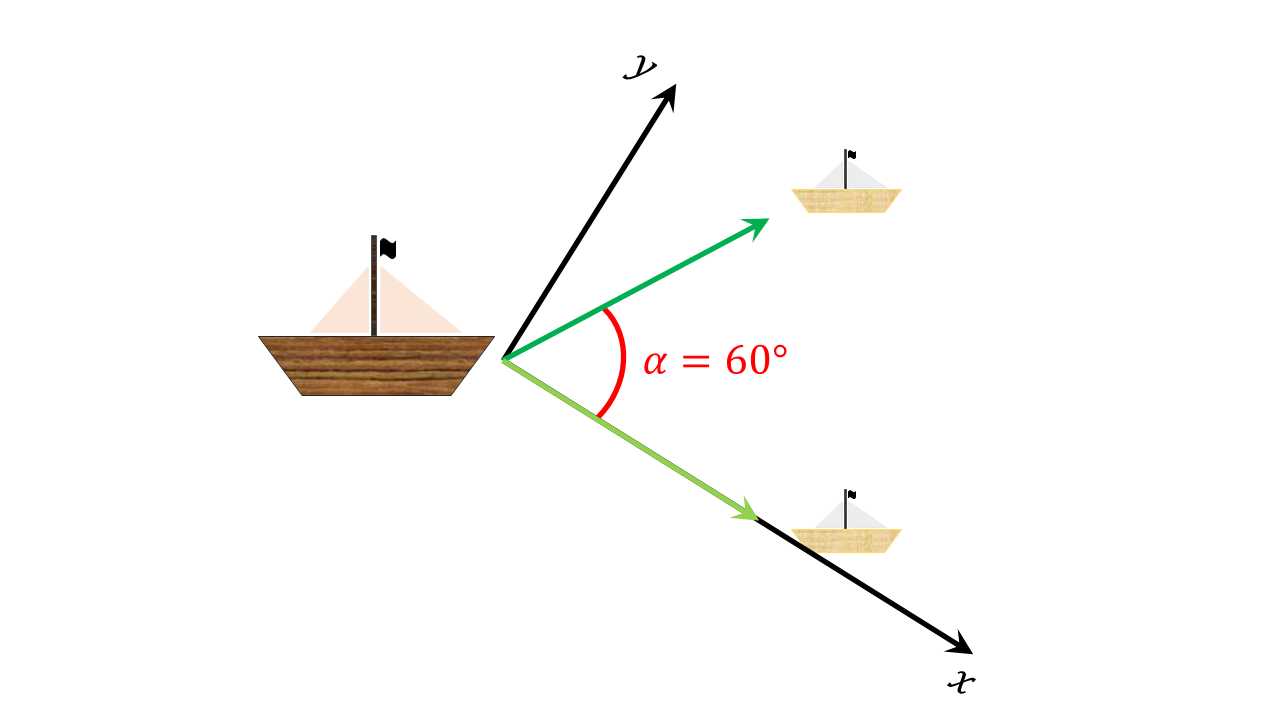
Zum einen kann man eine Achse auf die Verbindungslinie zwischen einem Schlepper und dem abgeschleppten Boot legen und die zweite Achse orthogonal dazu. Der Ursprung soll im abgeschleppten Schiff liegen. In diesem System hat die Kraft , mit der das Schiff in Richtung des ersten Abschleppbootes gezogen wird, nur eine Komponente in -Richtung, während die Kraft , die das Schiff durch das zweite Abschleppboot erfährt, sowohl eine Komponente in - als auch in -Richtung hat:
Für die resultierende Kraft , mit der das Schiff abgeschleppt wird, müssen nun die beiden Kräfte addiert werden. Man erhält den Vektor der resultierenden Kraft, und ihr Betrag kann berechnet werden:
Eine zweite Möglichkeit besteht darin, eine Koordinatenachse symmetrisch zwischen den beiden Schleppern durchzulegen. Die zweite Achse wird wieder im rechten Winkel zur ersten Achse gewählt. Hier muss darauf geachtet werden, dass der Winkel zwischen Koordinatenachse und Trosse richtig berücksichtigt wird.
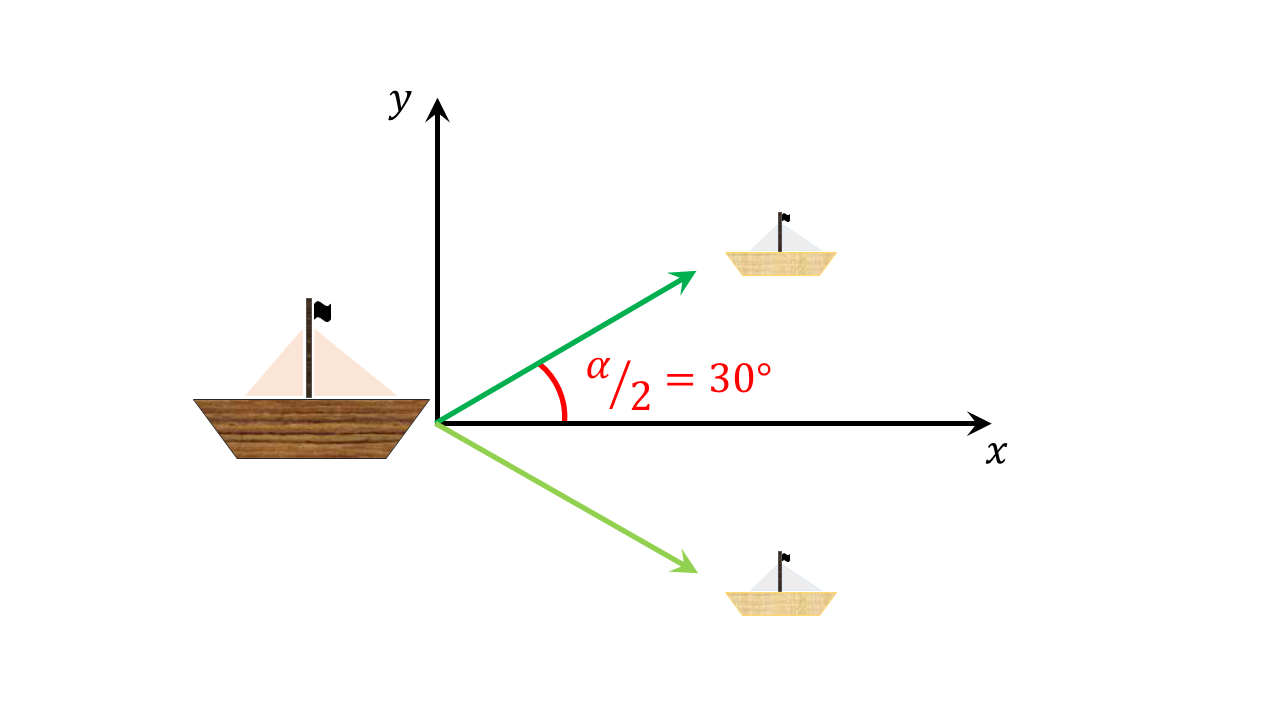
Die Kräfte, mit denen das Schiff gezogen wird, werden in dem zweiten Koordinatensystem beschrieben durch:
In diesem Koordinatensystem ergibt sich folgender Vektor für die resultierende Kraft:
Die Beschreibung des resultierenden Vektors unterscheidet sich in diesem System. Wenn das verwendete Koordinatensystem keinen Einfluss auf das Ergebnis hat, muss sich aber für den Betrag der resultierenden Kraft dasselbe wie oben ergeben:
Mit Hilfe von trigonometrischen Winkelbeziehungen kann die Gleichheit der beiden Ergebnisse gezeigt werden. Die Kraft, mit der das Schiff gezogen wird, ist also unabhängig vom gewählten Koordinatensystem.
Ein großes Schiff wird von zwei Schleppern mit Hilfe von Trossen in den Hafen gezogen. Der Winkel zwischen den beiden gleich langen Drahtseilen beträgt . Die Kräfte in den Trossen haben den gleichen Betrag. In der Abbildung ist die Situation skizziert.

Abbildung 4.1.108: Skizze des abgeschleppten Bootes (C)
Welches Koordinatensystem ist geeignet zur Beschreibung der Situation und damit zur Lösung eines Problems? Es sollen im Folgenden zwei mögliche Koordinatensysteme betrachtet und die resultierende Kraft und ihr Betrag allgemein berechnet werden.

Abbildung 4.1.109: Eine Koordinatenachse in Richtung eines Schleppers (C)
Zum einen kann man eine Achse auf die Verbindungslinie zwischen einem Schlepper und dem abgeschleppten Boot legen und die zweite Achse orthogonal dazu. Der Ursprung soll im abgeschleppten Schiff liegen. In diesem System hat die Kraft , mit der das Schiff in Richtung des ersten Abschleppbootes gezogen wird, nur eine Komponente in -Richtung, während die Kraft , die das Schiff durch das zweite Abschleppboot erfährt, sowohl eine Komponente in - als auch in -Richtung hat:
Für die resultierende Kraft , mit der das Schiff abgeschleppt wird, müssen nun die beiden Kräfte addiert werden. Man erhält den Vektor der resultierenden Kraft, und ihr Betrag kann berechnet werden:
Eine zweite Möglichkeit besteht darin, eine Koordinatenachse symmetrisch zwischen den beiden Schleppern durchzulegen. Die zweite Achse wird wieder im rechten Winkel zur ersten Achse gewählt. Hier muss darauf geachtet werden, dass der Winkel zwischen Koordinatenachse und Trosse richtig berücksichtigt wird.

Abbildung 4.1.110: Eine Koordinatenachse symmetrisch zwischen den Schleppern (C)
Die Kräfte, mit denen das Schiff gezogen wird, werden in dem zweiten Koordinatensystem beschrieben durch:
In diesem Koordinatensystem ergibt sich folgender Vektor für die resultierende Kraft:
Die Beschreibung des resultierenden Vektors unterscheidet sich in diesem System. Wenn das verwendete Koordinatensystem keinen Einfluss auf das Ergebnis hat, muss sich aber für den Betrag der resultierenden Kraft dasselbe wie oben ergeben:
Mit Hilfe von trigonometrischen Winkelbeziehungen kann die Gleichheit der beiden Ergebnisse gezeigt werden. Die Kraft, mit der das Schiff gezogen wird, ist also unabhängig vom gewählten Koordinatensystem.
Die Wahl des Koordinatensystems ist beliebig und beeinflusst das Ergebnis nicht. Jedoch kann die Bearbeitung eines Problems durch eine günstige Wahl des Koordinatensystems vereinfacht werden.
Basiswissen „Gebundene und freie Vektoren“
Wie schon besprochen, sind Vektoren durch einen Zahlenwert, eine zugehörige Einheit und eine Richtung gekennzeichnet. Bei der Behandlung von Problemen mittels Vektoren wird in der Praxis zwischen freien, linientreuen und gebundenen Vektoren unterschieden.
- Ein freier Vektor kann beliebig im Raum verschoben werden, dabei darf seine Richtung nicht verändert werden.
- Unter einem linienflüchtigen Vektor versteht man einen Vektor, der entlang seiner Wirkungslinie verschoben werden kann. Ein Beispiel dafür ist ein Kraftvektor, der an einem starren Körper angreift.
- Unter einem gebundenen Vektor versteht man einen Vektor, der an einen bestimmtem Punkt gebunden ist. Ein Richtungsvektor vom Ursprung aus, also ein Ortsvektor, ist ein gebundener Vektor. Ein weiteres Beispiel ist das Gravitationsfeld der Erde. Hier wird jedem Punkt im Raum ein Ortsfaktor und eine Richtung der Beschleunigung zugeordnet. Dieser Vektor ist an den Punkt gebunden und kann nicht im Raum verschoben werden.
Wenn in den folgenden Aufgabentexten nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie
Aufgabe 4.1.26
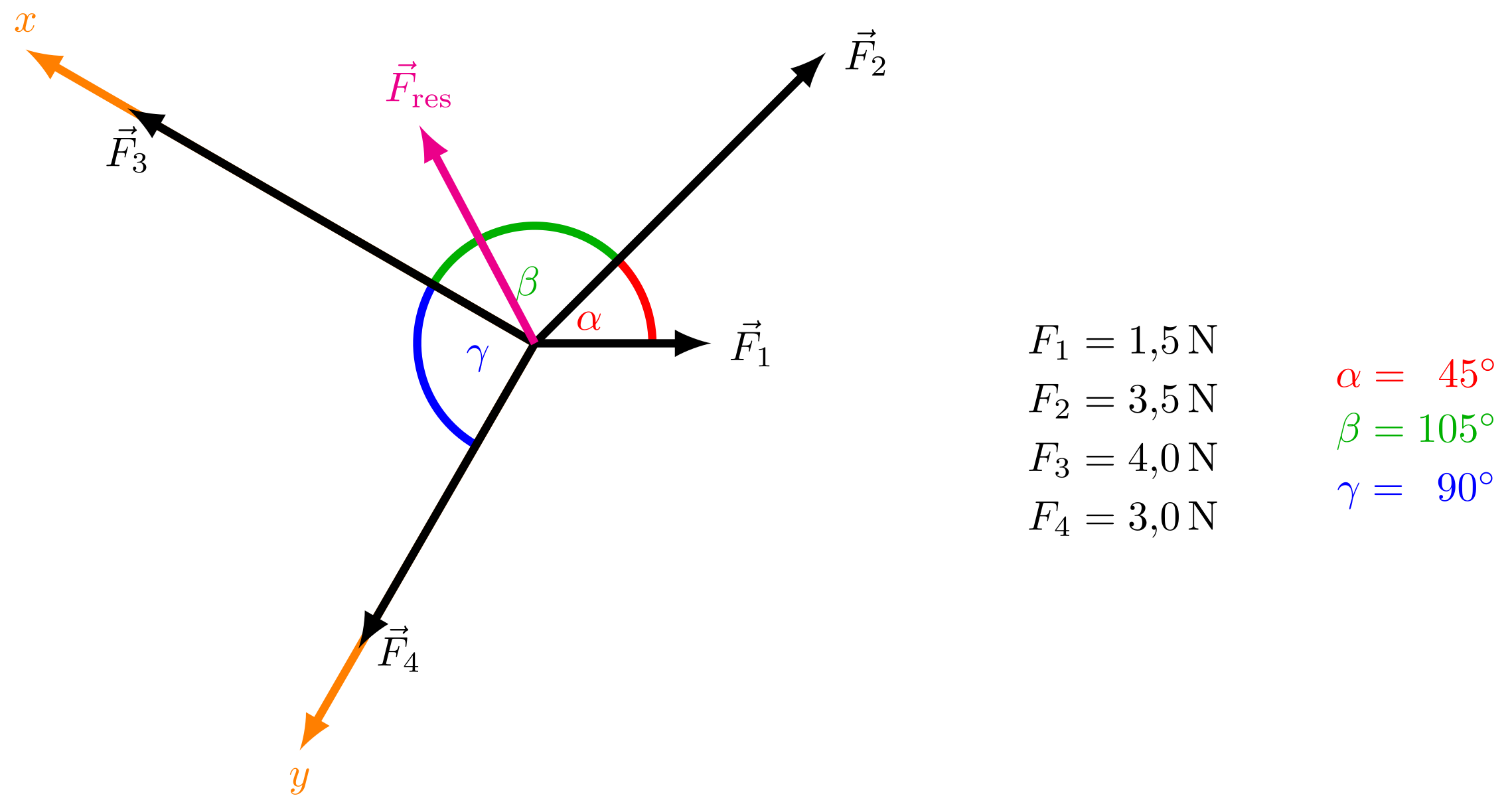
Vier Kräfte greifen an einem Punkt an. Die Beträge der Kräfte und ihre Richtungen relativ zueinander sind in der Abbildung skizziert.
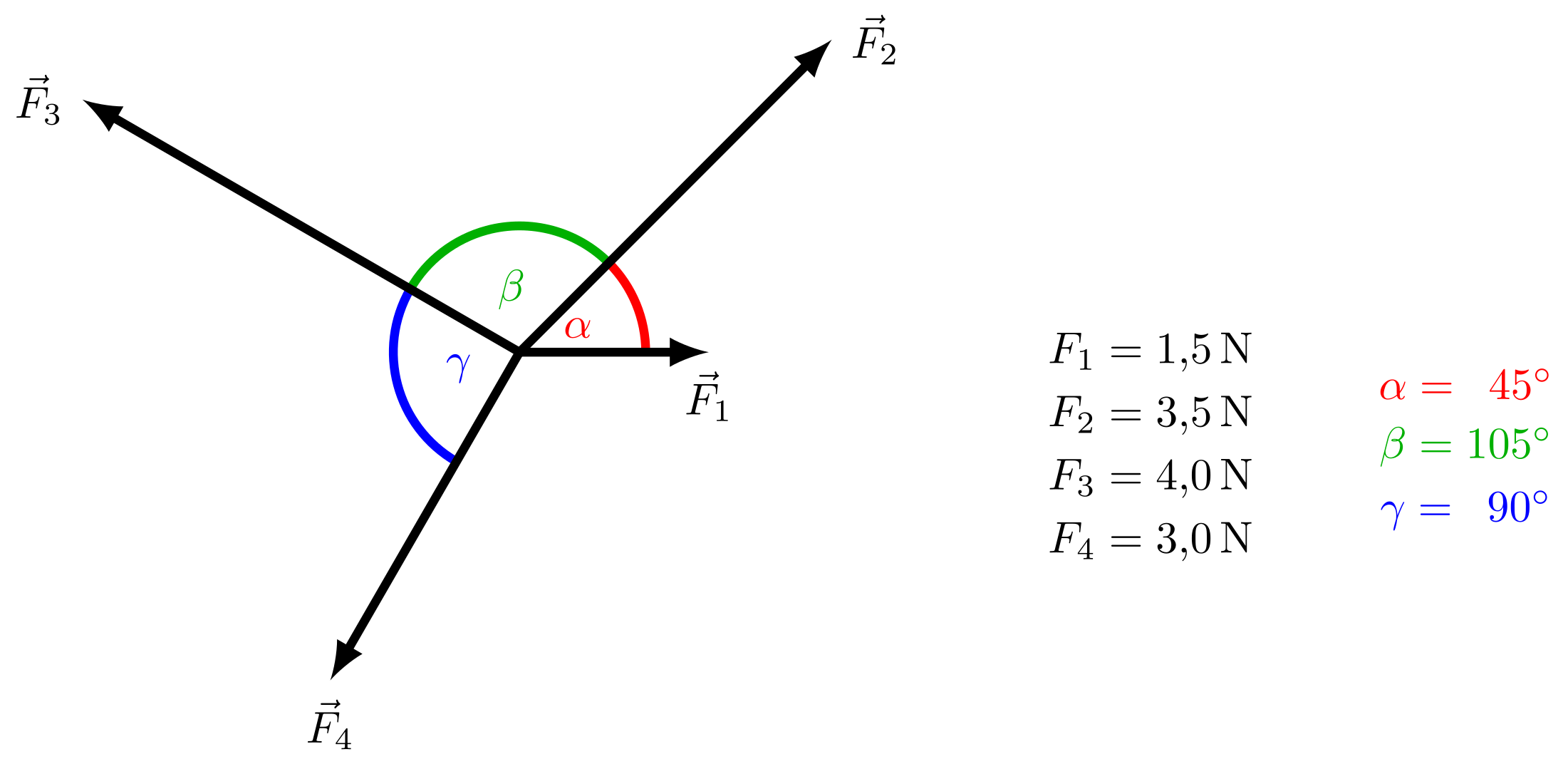
Stellen Sie die Kräfte als Vektoren in einem von Ihnen gewählten zweidimensionalen Koordinatensystem dar. Geben Sie den Betrag des resultierenden Kraftvektors in an.

Vier Kräfte greifen an einem Punkt an. Die Beträge der Kräfte und ihre Richtungen relativ zueinander sind in der Abbildung skizziert.

Abbildung 4.1.111: Zur Kräftedarstellung (C)
Komponenten einer Kraft (!)
Video 9: Komponenten einer Kraft (C)
.
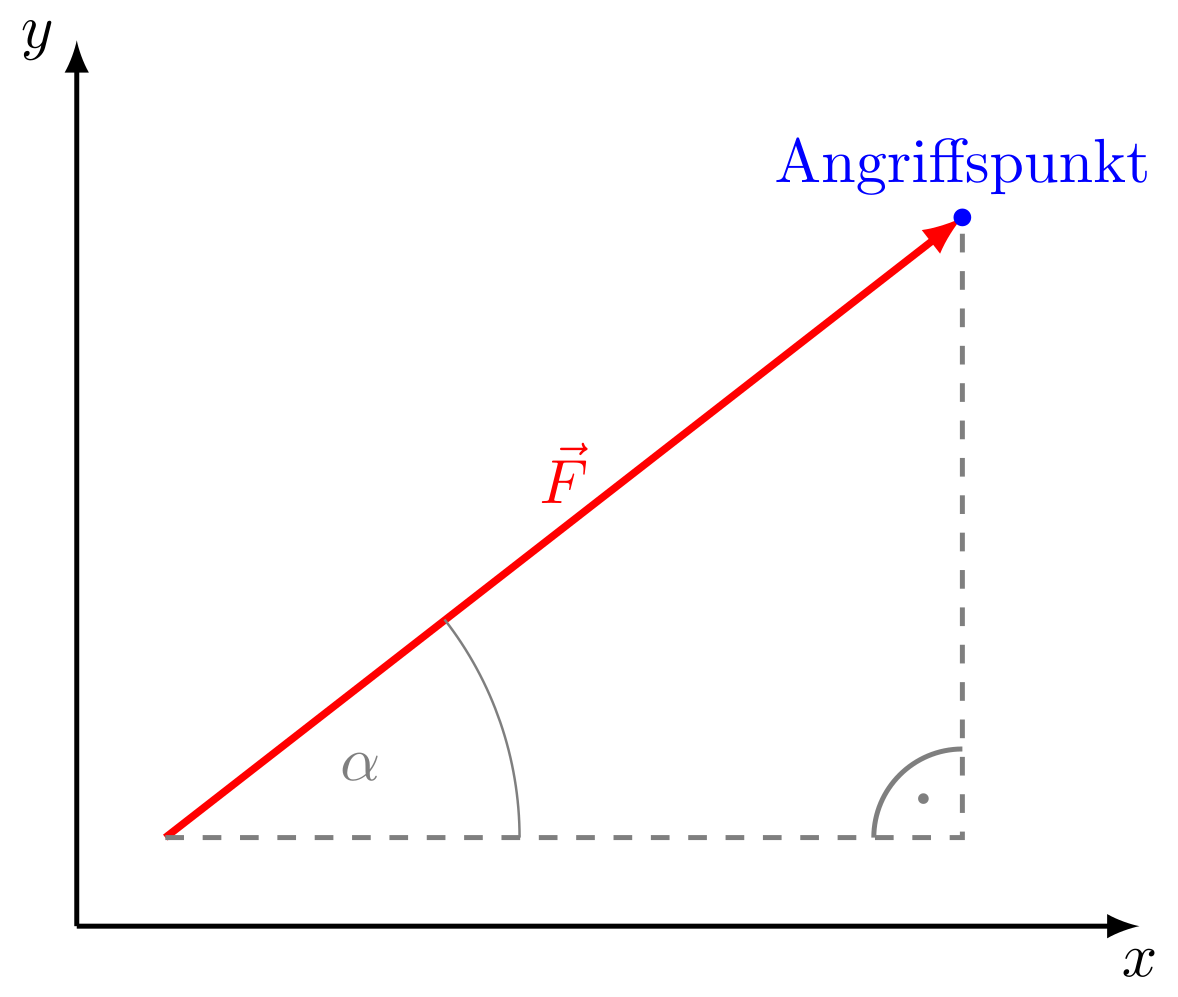
Abbildung 4.1.114: Komponenten einer Kraft (C)
Die Kraft ist eine vektorielle Größe (vgl. 4.1.1). In einem kartesischen Koordinatensystem wird der Kraftvektor durch seine Komponenten parallel zu den Koordinatenachsen festgelegt.
Ein Kraftvektor , der in der --Ebene liegt, besitzt folgende Komponenten:
wobei der von der positiven -Achse aus gegen den Uhrzeigersinn gemessene Winkel ist.
wobei der von der positiven -Achse aus gegen den Uhrzeigersinn gemessene Winkel ist.
Skizze: In der folgenden interaktiven Skizze wird die Zerlegung einer Kraft in ihre kartesischen Komponenten erläutert. Bewegen Sie durch Ziehen an dem Punkt den Kraftvektor und veranschaulichen Sie sich so die Aufspaltung in die beiden Komponenten.
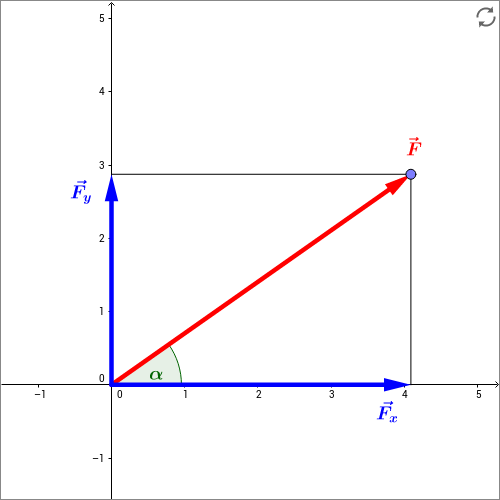
Kräftezerlegung (!)
Das Video zu Zerlegung in nicht-kartesische Komponenten wird überarbeitet.
Video 10: Zerlegung mit Trigonometrie (C)
.
Video 11: Symmetrische Zerlegung (C)
.
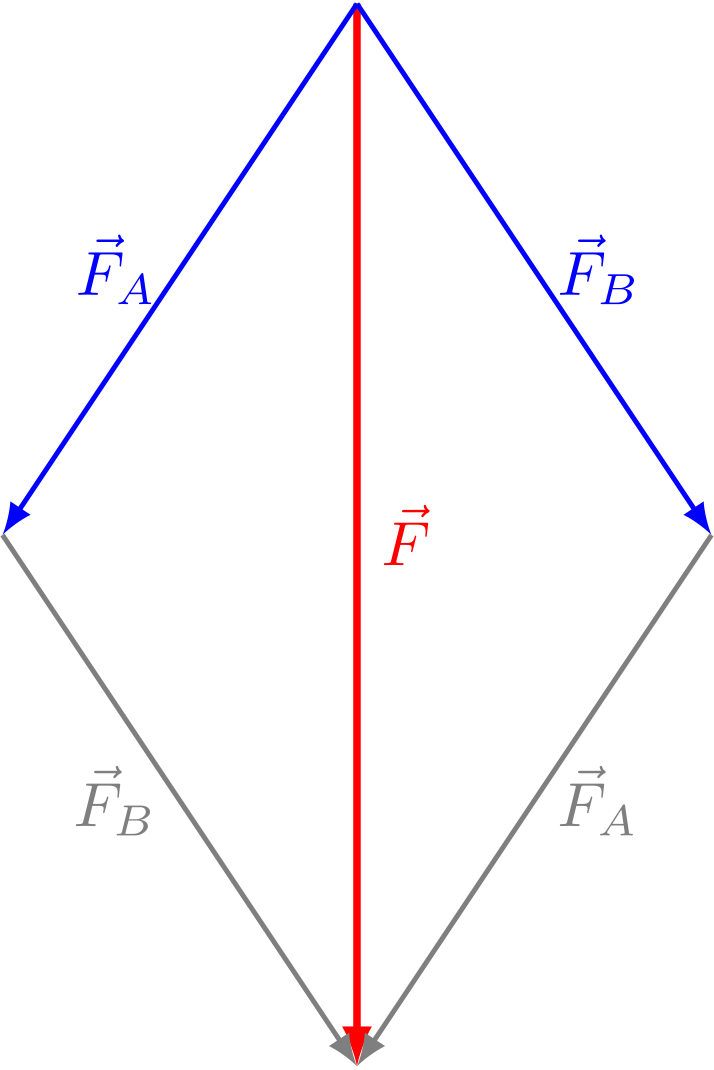
Abbildung 4.1.116: Zerlegung einer Kraft (C)
Bei der Zerlegung eines Kraftvektors in seine kartesischen Komponenten stehen die zwei Teilkräfte senkrecht aufeinander. Man kann Kraftvektoren jedoch auch in zwei Teilkräfte aufspalten, die nicht senkrecht zueinander stehen. Ein Beispiel aus der Praxis wäre ein Gewicht, das mit Hilfe von zwei Seilen gehalten wird, die nicht parallel liegen, sondern in verschiedene Richtungen verlaufen. Weil ein Seil eine Kraft nur längs seines Verlaufs aufnehmen kann, muss die Gewichtskraft des Körpers vektoriell in die beiden Seilrichtungen zerlegt werden.
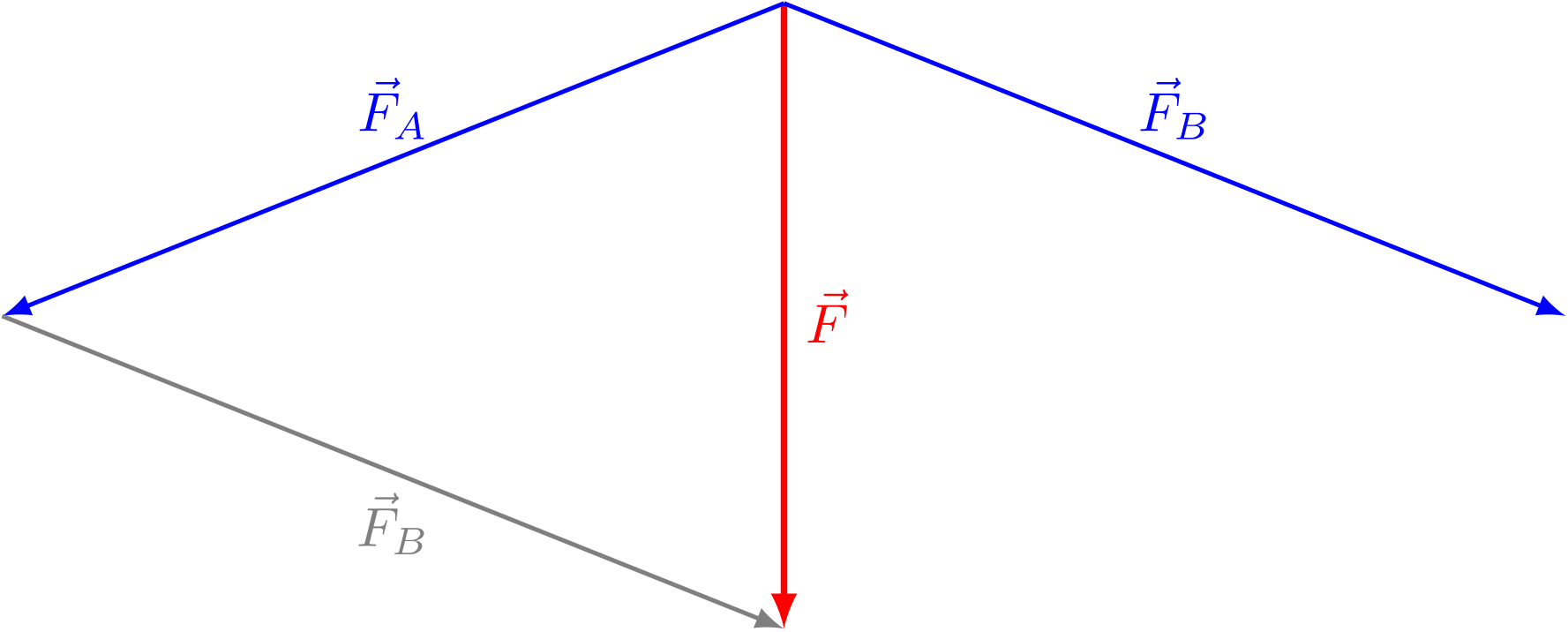
Abbildung 4.1.117: Zerlegung einer Kraft (C)
Wie kann nun für jedes der beiden Seile die Teilkraft berechnet werden, die von ihm aufgenommen werden muss? Die beiden Seilkräfte und die Gewichtskraft müssen einander kompensieren. Aneinandergelegt bilden die Vektoren daher ein Dreieck. Eine Länge des Dreiecks ist durch die Gewichtskraft vorgegeben, die Winkel des Dreiecks erhält man aus der Geometrie des vorliegenden Beispiels. So ist das Dreieck festgelegt und damit auch die zwei Seilkräfte.
Wie können nun die Kräfte ermittelt werden, die die beiden Seile jeweils aufnehmen? Da die Vektoren der beiden Seilkräfte sich zur Gesamtkraft addieren, bilden die beiden Teilkräfte und die Gesamtkraft ein geschlossenes Dreieck. Von diesem Dreieck ist die Länge einer Seite bekannt, nämlich die Gesamtkraft. Die Längen der beiden anderen Seiten (und damit die Größen der beiden Teilkräfte) liegen fest, wenn die Winkel bekannt sind, unter denen die Seile relativ zur Richtung der Gesamtkraft liegen.
Alternativ kann man sich überlegen, dass sich die horizontalen Komponenten der Seilkräfte, also senkrecht zur Gewichtskraft, gerade gegenseitig aufheben müssen. Ihre senkrechten Komponenten, also parallel zur Gewichtskraft, müssen sich gerade zur Gewichtskraft addieren. Damit sind die beiden Teilkräfte ebenfalls eindeutig festgelegt.
Skizze: Die folgende interaktive Skizze zeigt die Zerlegung einer Gesamtkraft in zwei Teilkräfte. Die Gesamtkraft wurde ohne Beschränkung der Allgemeinheit in Richtung der positiven -Achse gelegt. Nun soll diese Kraft in zwei Teilkräfte entlang zweier vorgegebener Richtungen zerlegt werden, die durch die gestrichelten Linien gekennzeichnet sind. Sie sehen die beiden resultierenden Teilkräfte sowie das von ihnen gebildete Kräfte-Parallelogramm, das Sie schon aus der Vektoraddition kennen. Ebenfalls eingezeichnet sind in Schwarz die Komponenten der Teilkräfte, die senkrecht zur Richtung der Gesamtkraft stehen und sich gegenseitig aufheben, sowie in Rot die Komponenten, die sich zur Gesamtkraft summieren.
Durch Ziehen an den blauen Punkten können Sie die Richtungen der gestrichelten Linien verschieben. Ziehen Sie zunächst die rechte Linie nach unten. Die Teilkraft auf der linken Seite muss größer werden, um den dadurch reduzierten Beitrag der rechten Teilkraft zur Gesamtkraft auszugleichen. Ziehen Sie die rechte Linie nun noch weiter bis unter die -Achse. Es entsteht eine Konfiguration, in der die Komponente der rechten Teilkraft, die zur Gesamtkraft beiträgt (rot), sogar entgegen der Gesamtkraft gerichtet ist! Bei der Aufteilung einer Kraft in zwei Teilkräfte kann also eine der beiden Kräfte sogar der ursprünglichen Kraft entgegen wirken. Ziehen Sie noch weiter und beobachten Sie das Anwachsen der beiden Teilkräfte. Bei Winkeln zwischen den beiden Teilkräften von oder größer ist die Aufteilung aber nicht mehr möglich.
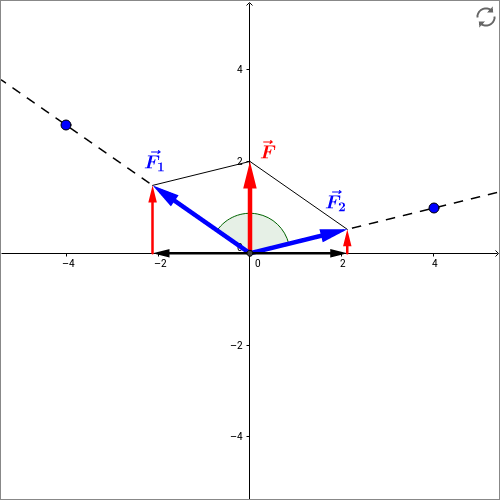
Gewicht am Seil
Video 12: Gewicht am Seil (C)
.
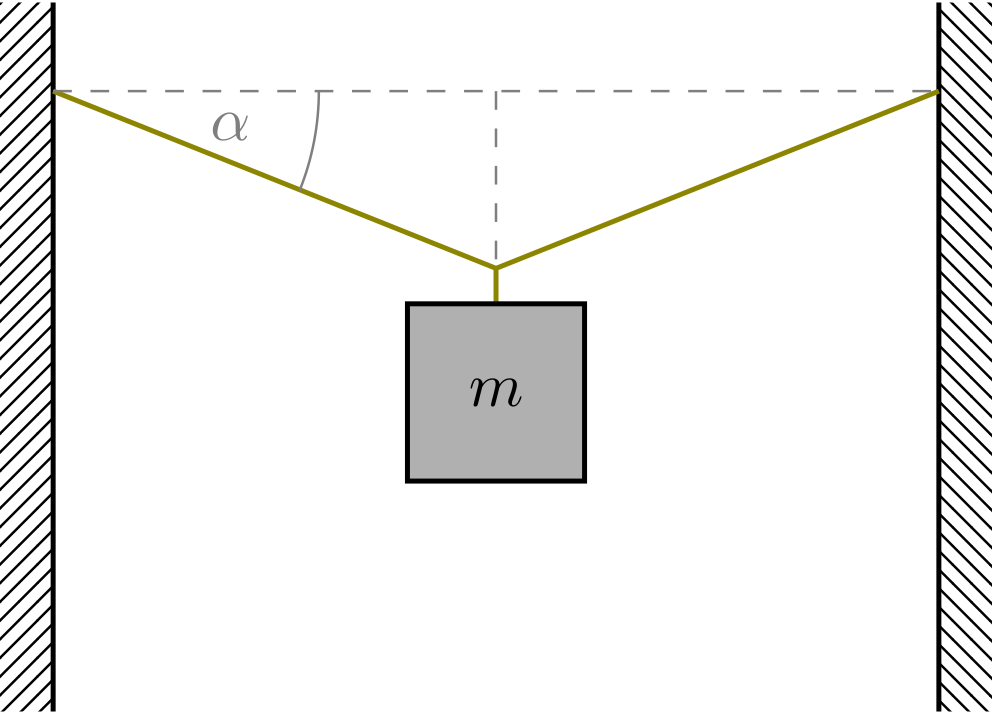
Abbildung 4.1.119: Gewicht an durchhängendem Seil (C)
Ein schönes Beispiel für die Zerlegung einer Kraft ist die Frage, wie bei einem Körper, der an einem durchhängenden Seil hängt, die Gewichtskraft auf die beiden Seilenden aufgeteilt wird. Wir haben oben schon gesehen, dass die Teilkräfte um so größer werden, je näher der Winkel zwischen den beiden sich nähert, je flacher also die Aufhängung ist. Denken Sie an eine Wäscheleine, an der ein schweres Wäschestück hängt und die Sie durch Ziehen an einer Seite spannen möchten. Je gerader die Wäscheleine wird, d.h. je kleiner der Knick zwischen den Leinen auf beiden Seiten des Wäschestücks wird, um so stärker müssen Sie die Leine spannen.
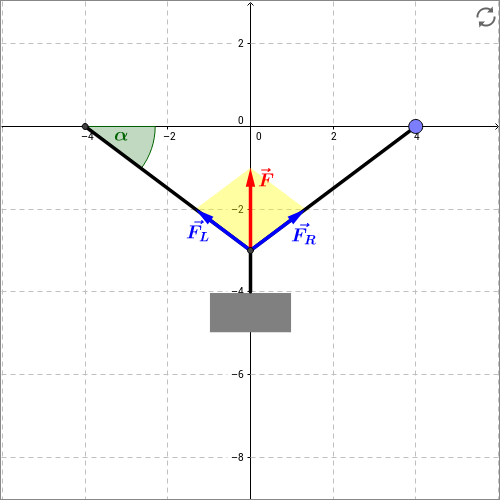
Skizze: In der folgenden interaktiven Skizze können Sie dies nachvollziehen. Eingezeichnet ist die Kraft , die benötigt wird, um die Gewichtskraft des angehängten Körpers zu halten. Die Kraft wird auf die beiden Seile übertragen und bewirkt dort die Seilkräfte und . Durch Ziehen am blauen Punkt können Sie die Aufhängung flacher und steiler machen. Wenn Sie den blauen Punkt nach links ziehen, nähern sich die Aufhängepunkte einander an. Bei senkrechten Seilen übernimmt jedes der beiden Seile die Hälfte der Gesamtkraft . Umgekehrt nähern sich beim Auseinanderziehen der Aufhängepunkte die Seile zunehmend der Horizontalen an. Die Teilkräfte werden immer größer.
Video 13: Beispiel hängendes Wäschestück (C)
.
Beispiel
4.1.27
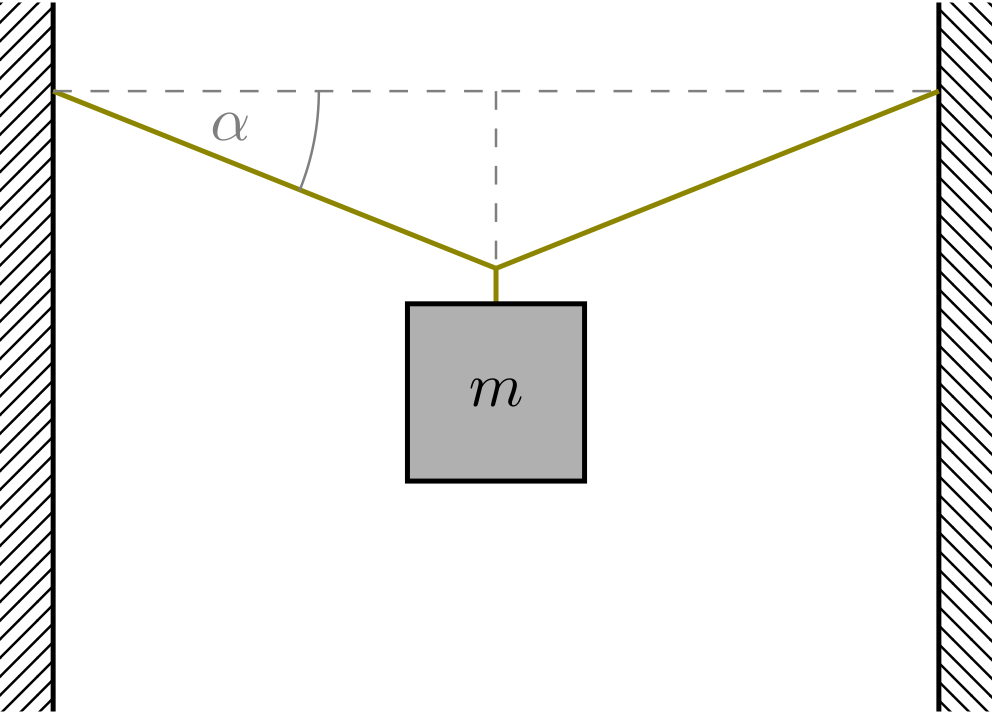
Ein Wäschestück der Masse wird mittig an eine Wäscheleine gehängt, wobei die beiden Seilstücke rechts und links des Wäschestücks jeweils einen Winkel von relativ zur Horizontalen einnehmen. Wie groß ist die Kraft in den beiden Seilstücken?
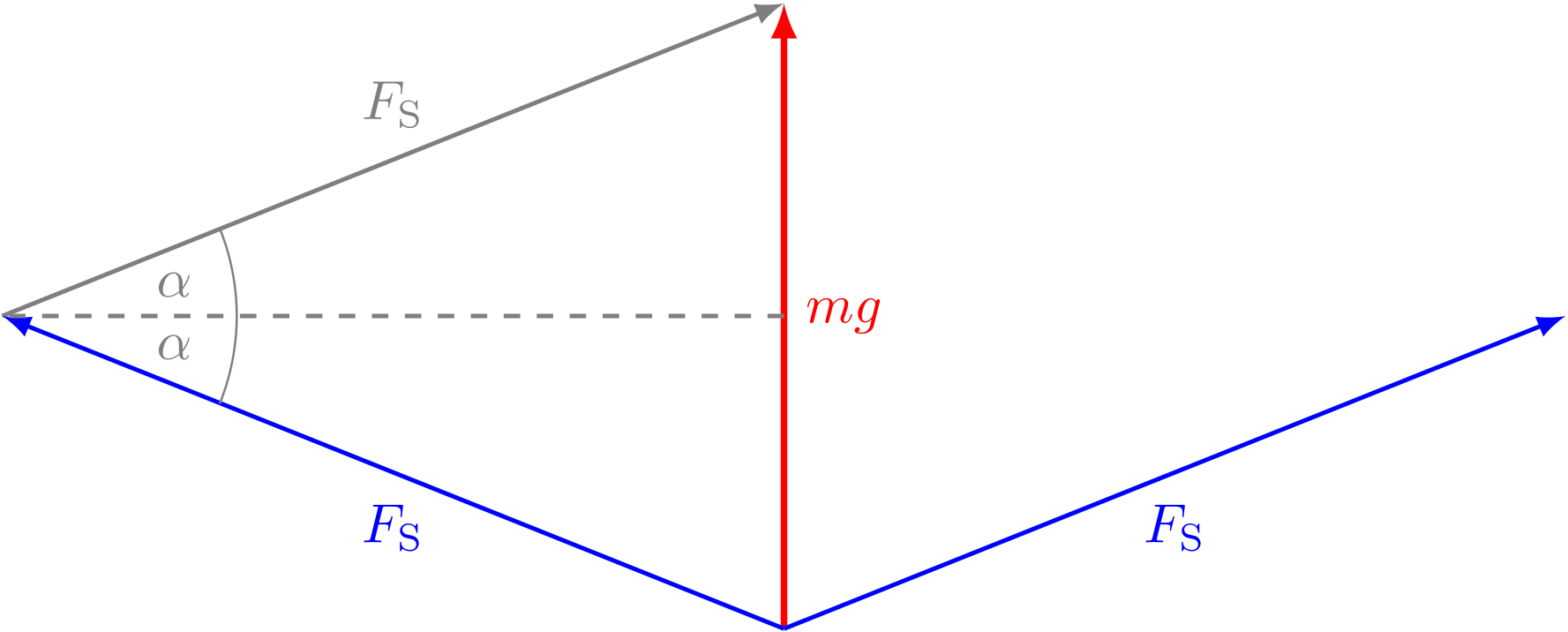
Da die Aufhängung symmetrisch ist, übernimmt jedes der beiden Seilstücke die Hälfte der vertikalen Kraftkomponente.

Abbildung 4.1.121: Wäschestück wird am Seil aufgehängt (C)
Ein Wäschestück der Masse wird mittig an eine Wäscheleine gehängt, wobei die beiden Seilstücke rechts und links des Wäschestücks jeweils einen Winkel von relativ zur Horizontalen einnehmen. Wie groß ist die Kraft in den beiden Seilstücken?

Abbildung 4.1.122: Kraftkomponenten auf die Seilstücke (C)
Da die Aufhängung symmetrisch ist, übernimmt jedes der beiden Seilstücke die Hälfte der vertikalen Kraftkomponente.
Schiefe Ebene (!)
Ein typisches Beispiel für die Zerlegung einer Kraft in ihre Komponenten ist die Betrachtung der schiefen Ebene. Eine kurze, auf die hier betrachtete Problemstellung zugeschnittene Behandlung von Kräften in der Technischen Mechanik finden Sie auf Seite 4.1.10.
Das Video zu Schiefe Ebene wird überarbeitet.
In Beispiel 4.1.20 wurde ein Holzklotz auf einer geraden Ebene betrachtet. Wir wollen nun die Ebene etwas um den Winkel neigen:
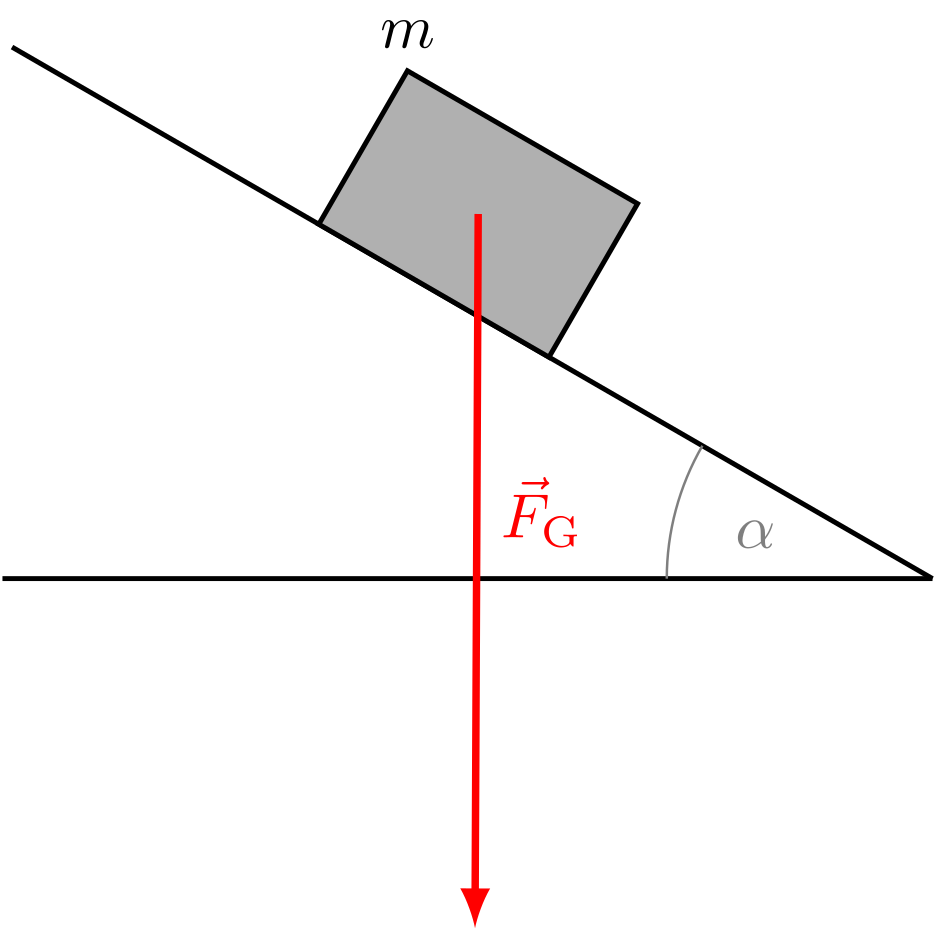
Die Gewichtskraft zeigt weiterhin nach unten. Wir fragen uns aber, welche Kraft die Ebene nun aufbringen muss. Zunächst ist uns klar: Die Kraft wird wohl kleiner werden je größer die Neigung wird. Wenn wir die Ebene schließlich um kippen, verschwindet sie ganz.
Zu Hilfe kommt uns die Kräftezerlegung. Wir zerlegen die Gewichtskraft in eine Komponente senkrecht zur Oberfläche und eine Komponente parallel zur Oberfläche.
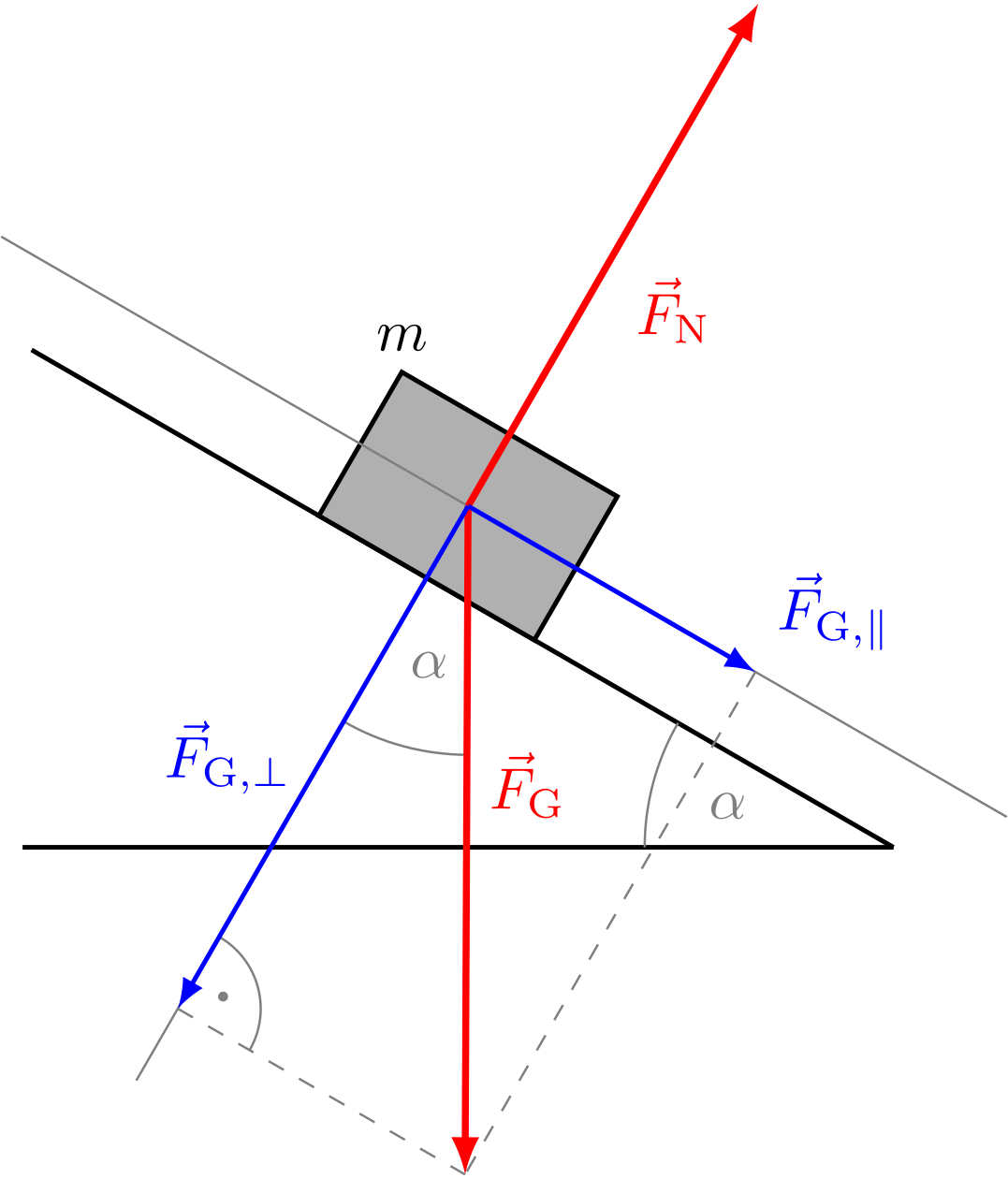
Abbildung 4.1.124: Zerlegung der Gewichtskraft auf der schiefen Ebene (C)
Mit der Trigonometrie im rechtwinkligen Dreieck gilt für die Beträge der Komponenten von
Die Gewichtskraft zeigt zum Erdmittelpunkt, also senkrecht nach unten zur Erdoberfläche (siehe untere Skizze). Wir sehen, dass die Kraft gerade die Komponente ausgleichen muss, d.h. die senkrecht zur Auflagefläche stehende Komponente der Gewichtskraft wird durch die Normalkraft kompensiert. So wird verhindert, dass der Körper in die Ebene eindringt. Man nennt eine solche Art von Kraft auch eine Zwangskraft (), da sie sicherstellt, dass sich der Körper nur parallel zur vorgegebenen Ebene bewegen kann.
Aus der Erfahrung wissen wir, dass die Kiste auf einer glatten Oberfläche herunterrutscht, wenn diese geneigt ist. Verantwortlich hierfür ist die Komponente parallel zur Oberfläche. Damit der Körper im Gleichgewicht ist und nicht durch beschleunigt wird, müssen wir diese Komponente noch kompensieren.
Ist die Masse der Kiste nicht allzu groß, können wir diese z.B. mit unseren Händen festhalten in dem wir zum Beispiel am Körper ziehen. Die Kraft die wir dabei mit unseren Händen aufwenden, muss entgegengesetzt zu und gleich groß sein.
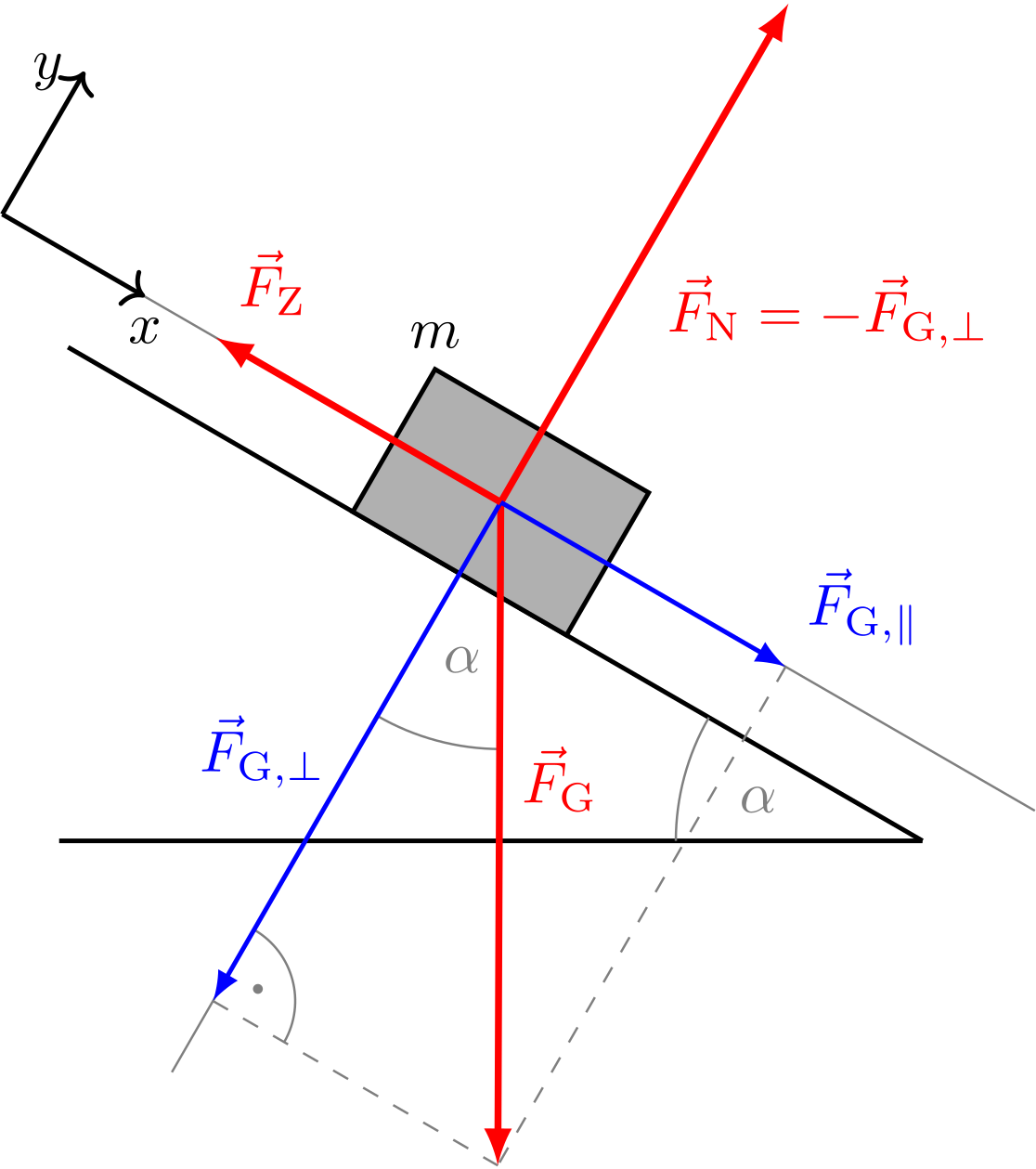
Abbildung 4.1.125: Kompensation der Hangabtriebskraft (C)
Wenn wir berücksichtigen, wie die Kräfte im Bezug auf das oben eingezeichnete Koordinatensystem liegen (insbesondere in positive oder negative Koordinatenrichtung), ergibt sich für das Kräftegleichgewicht
Damit können die Beträge von und bestimmt werden zu
Wird der parallele Anteil nicht kompensiert könnte dies zum Beispiel zu einer Verschiebung des Körpers führen. Dieser parallele Anteil wird als Hangabtriebskraft bezeichnet, es gilt also
- Normalkraft :
Dies ist das Negative der Kraft, mit der der Körper auf der Ebene aufliegt.
Die Normalkraft ist immer senkrecht, d.h. normal zur Ebene gerichtet.
-
Hangabtriebskraft :
Dies ist die Kraft, die den Körper die Ebene entlang bewegt.
Die Hangabtriebskraft ist immer parallel zur Ebene gerichtet, und zwar abwärts.
Normalkraft und Hangabtriebskraft stehen senkrecht aufeinander.
Aus der Skizze kann man ablesen, dass der Winkel zwischen der schiefen Ebene und der Horizontalen auch der Winkel ist, den die Gewichtskraft relativ zum gedrehten Koordinatensystem einnimmt. Man kann dies aus der Geometrie verstehen, da Gewichtskraft und Horizontale bzw. Normalkraft und Hangebene jeweils paarweise aufeinander senkrecht stehen.
Für die Hangabtriebskraft und die Normalkraft erhält man somit:
Für (kein Hang) ergibt sich , d.h. die Hangabtriebskraft verschwindet.
Für (senkrechter Hang) ergibt sich , d.h. die Hangabtriebskraft ist gleich der Gewichtskraft.
Die Ergebnisse für die beiden Grenzfälle erscheinen sinnvoll.
Skizze: In der folgenden interaktiven Skizze wird für einen Körper auf der schiefen Ebene die Aufspaltung der Gewichtskraft in die beiden Komponenten Normalkraft und Hangabtriebskraft erläutert. Ändern Sie durch Ziehen des blauen Punkts auf der -Achse die Steigung des Hangs und beobachten Sie, wie sich dabei die Aufteilung der Gewichtskraft in die beiden Komponenten ändert.
Das Video zu Beispiel schiefe Ebene wird überarbeitet.
Beispiel
4.1.28
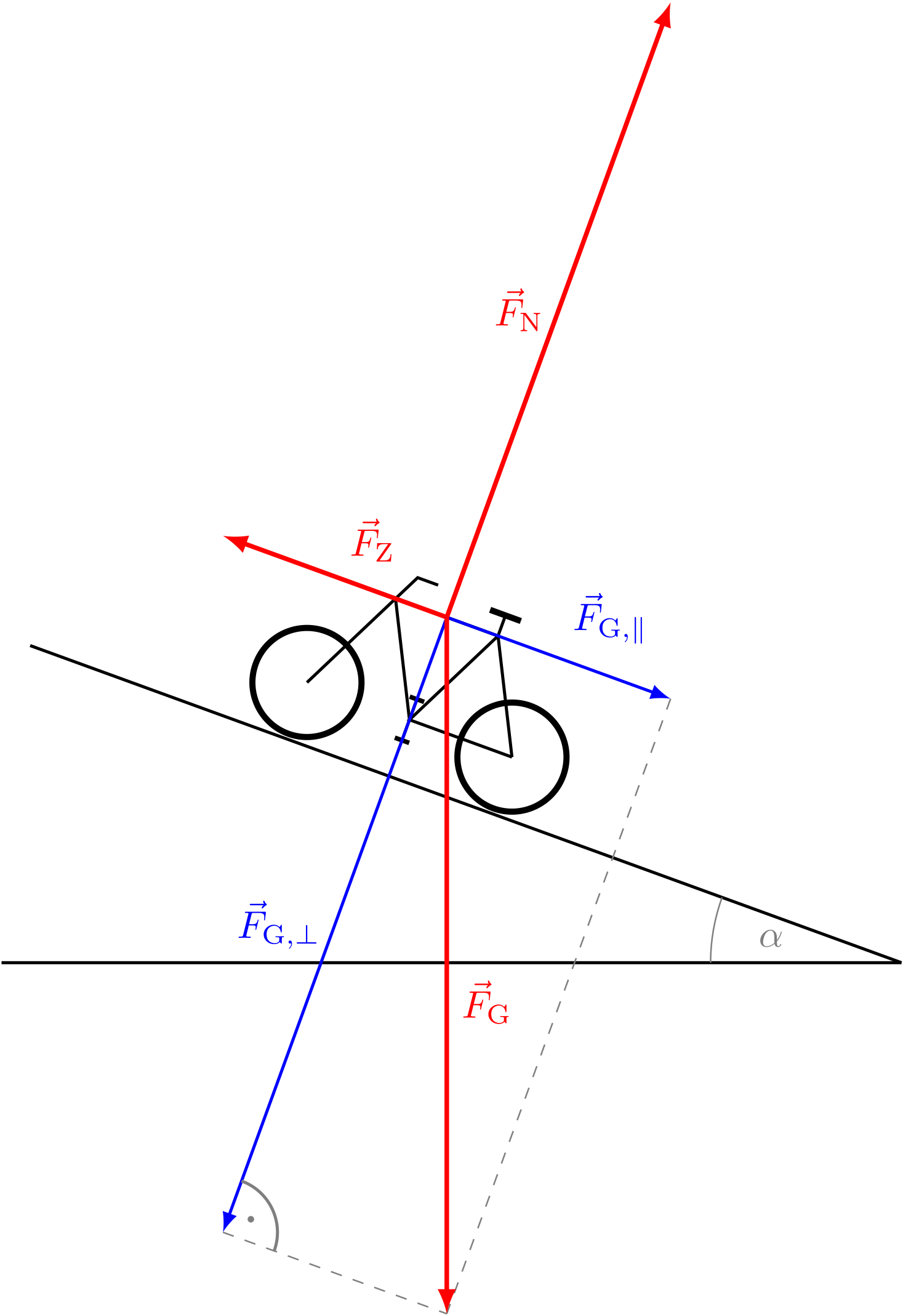
Welche Kraft muss man aufwenden, um ein Fahrrad mit der Masse eine Straße mit der Steigung hinaufzuziehen?

Die Steigung ist gegeben durch den Tangens des Winkels relativ zur Horizontalen:

Abbildung 4.1.126: Fahrrad wird Steigung hochgezogen (C)
Welche Kraft muss man aufwenden, um ein Fahrrad mit der Masse eine Straße mit der Steigung hinaufzuziehen?

Abbildung 4.1.127: Zur Bestimmung des Steigungswinkels (C)
Die Steigung ist gegeben durch den Tangens des Winkels relativ zur Horizontalen:
Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie .
Falls nicht anders angegeben, verwenden Sie