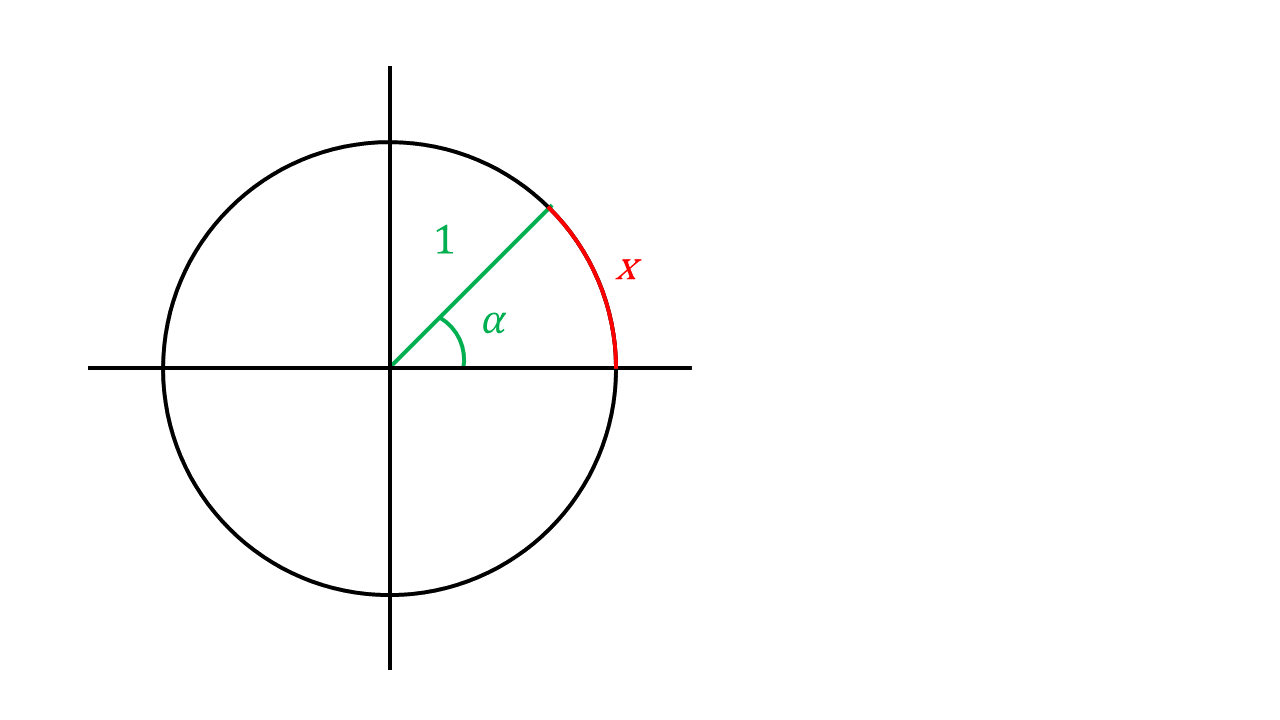2. Mechanik
  3. Drehbewegungen
  4. Kreisbewegungen (+)

4.5.1 Kreisbewegungen





 

Basiswissen „Kreisbewegung“


Für die Beschreibung von Bewegungen ist die Kenntnis der Bahn wichtig. Bei einer geradlinigen gleichförmigen Bewegung legt ein Körper in eine Richtung eine Strecke Δs in einer Zeit Δt zurück. Entlang der Strecke ist seine Geschwindigkeit v= Δs Δt konstant. Diese Überlegungen sollen nun auf die Bewegung auf einer Kreisbahn übertragen werden.

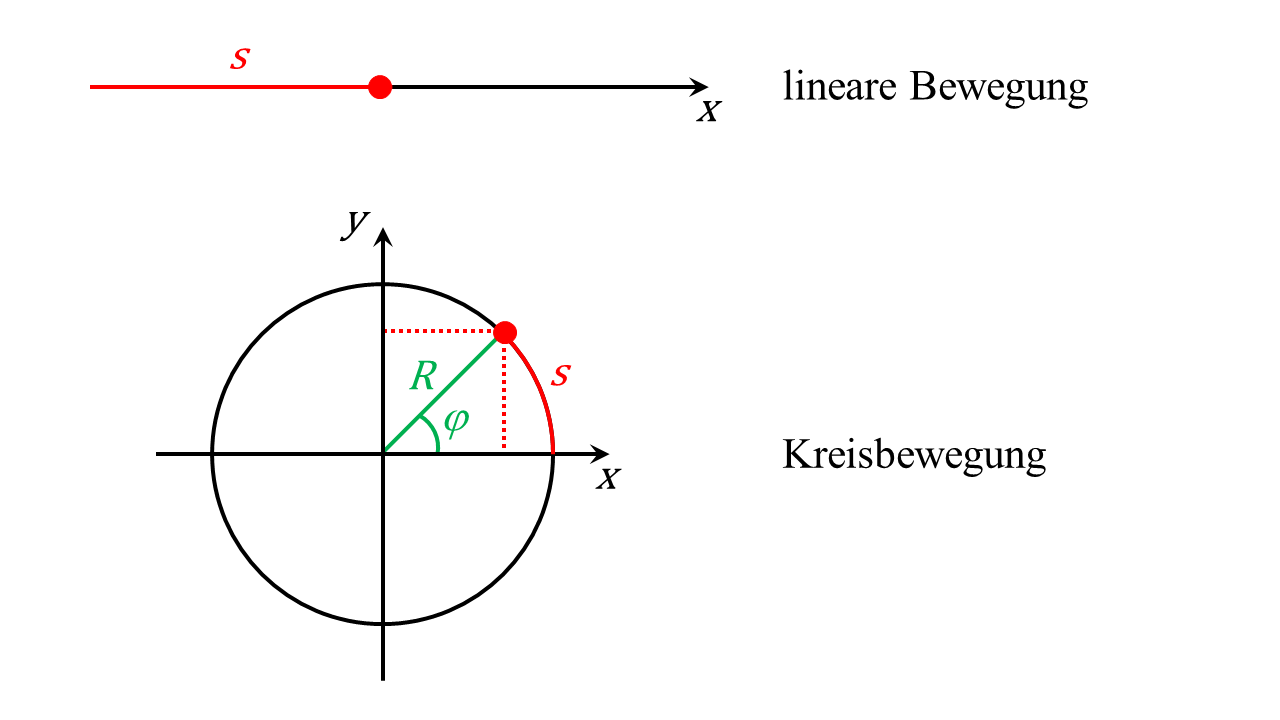
././Physikkurs/drehbewegung_kreisbewegungen/images/Drehbewegungen.png
Abbildung 4.5.1: Skizze zu Drehbewegungen (C)



Der auf einer Kreisbahn mit dem Radius R zurückgelegte Weg s beträgt abhängig vom überstrichenen Winkel φ:

s=R·φ .

Die Einheit des Winkels ist [φ]=rad=1.
Der zurückgelegte Weg s ist also der Winkel φ multipliziert mit dem Radius. Dabei wird der Winkel im Bogenmaß angegeben und bei einer vollen Kreisbahn ergibt sich gerade der Umfang eines Kreises s Kreis =2·π·R. Der Radius R ist bei einem Kreis eine konstante Größe, während sich der Winkel φ entlang der Bahn permanent ändert. Deshalb wird bei einer Kreisbahn anstelle des Kreisbogens s der überstrichene Winkel φ als Variable verwendet. Allgemein werden Radius R und Winkel φ als Polarkoordinaten bezeichnet.



Analog zur gleichförmigen Bewegung kann eine Bewegung entlang einer Kreisbahn mit einer konstanten Bahngeschwindigkeit |v| stattfinden. In gleichen Zeiten Δt werden also gleiche Wegstrecken Δs=R·Δφ zurückgelegt. Da der Radius konstant ist, müssen in gleichen Zeiten gleiche Winkel überstrichen werden.
Bei einer gleichförmigen Kreisbewegung ist der Betrag der Bahngeschwindigkeit |v| konstant und es ist:

|v|= Δs Δt =R· Δφ Δt  .

Der Quotient aus überstrichenem Winkel Δφ und verstrichener Zeit Δt wird als Winkelgeschwindigkeit ω bezeichnet:

ω= Δφ Δt  .

Die Einheit der Winkelgeschwindigkeit ist [ω]= rad s = 1 s .


Beispiel 4.5.1  
Die Erde dreht sich an einem Tag einmal um sich selbst. Der Radius der Erde beträgt etwa R=6370 km. Welchen Betrag hat ihre Bahngeschwindigkeit |v| und mit welcher Winkelgeschwindigkeit ω bewegen Sie sich, wenn Sie am Äquator in der Hängematte liegen?
Für die Bahngeschwindigkeit muss lediglich der zurückgelegte Weg Δs durch die dafür benötigte Zeit Δt geteilt werden. Während einer vollen Drehung der Erde um sich selbst vergehen etwa

Δt=24 h=24·60·60 s .

Ein Punkt an der Oberfläche am Äquator bewegt sich während dieser Drehung auf einer Kreisbahn mit dem Radius R. Die zurückgelegte Wegstrecke beträgt also
 
Δs=2·π·R=​ 2·π·6370·1000 m .
 
Damit liegt der Betrag der Bahngeschwindigkeit bei:
 
|v|= Δs Δt ​ = 2·π·6370·1000 m 24·60·60 s ​≈463  m s  .
 
Ein Umlauf entspricht einem Winkel von 360 ∘ . Im Bogenmaß sind das 2·π rad. Es ergibt sich für die Winkelgeschwindigkeit also:
 
ω= Δφ Δt ​ = 2·π rad 24·60·60 s ​≈7,27· 10-5   rad s  .
 
Auch bei einer Bewegung auf einer Kreisbahn ist es möglich, das sich der Körper während eines Zeitintervalls immer schneller bewegt. Als Beispiel kann hier das Rotorblatt eines Helikopters dienen. Vor dem Start ist der Rotor in Ruhe. Dann beginnt der Rotor sich zu drehen und dreht sich immer schneller, bis der Helikopter starten kann.
Beschleunigt der Körper entlang seiner Kreisbahn, wird die Änderung der Winkelgeschwindigkeit pro Zeitintervall als Winkelbeschleunigung α definiert:

α= Δω Δt  .

Die Einheit der Winkelbeschleunigung ist [α]= rad s2 = 1 s2 .


Beispiel 4.5.2  
Sie fahren mit Ihrem Fahrrad mit einer Geschwindigkeit von v1 =24 km/h. Während Δt=6,5 s beschleunigen Sie mit einer konstanten Beschleunigung, bis Sie eine Geschwindigkeit von v2 =43 km/h erreicht haben. Die Räder an Ihrem Fahrrad haben einen Radius von R=0,30 m.
Welchen Weg s legen Sie zurück, welchen Wert hat Ihre Beschleunigung a und welchen Winkel φ überstreicht ein Punkt am Rand des Rades während der Zeit Δt?
Mit den Gesetzen, die bei einer gleichförmig beschleunigten Bewegung gelten, wird der zurückgelegte Weg berechnet:
 
s= v1 ·Δt+ 1 2 ·a·(Δt )2    und    v2 = v1 +a·Δt .
 
Umformen der zweiten Beziehung ergibt die Beschleunigung a:

a = v2 - v1 Δt = 43  km h -24  km h 6,5 s = 19· 1 3,6   m s 6,5 s ≈ 0,81  m s2  .

Durch Einsetzen der Beschleunigung in die erste Gleichung kann der zurückgelegte Weg bestimmt werden:

s = v1 ·Δt+ 1 2 · v2 - v1 Δt ·(Δt )2 = v1 ·Δt+ 1 2 ·( v2 - v1 )·Δt = 1 2 ·( v2 + v1 )·Δt = 1 2 ·(43+24)  km h ·6,5 s = 1 2 ·67· 1 3,6   m s ·6,5 s ≈ 60,5 m .

Der während der Beschleunigung überstrichene Winkel kann aus dem zurückgelegten Weg bestimmt werden:

s = R·φ   ⟺   φ= s R  , φ ≈ 60,5 m 0,3 m ≈200 rad .



Die bei der gleichförmigen und gleichmäßig beschleunigten Bewegung und die bei einer Kreisbewegung entsprechenden Größen sind in der folgenden Tabelle einander gegenübergestellt. Die Richtung der Geschwindigkeit v T und der Beschleunigung a T ist immer tangential zur Bahnkurve.
lineare Bewegung Kreisbewegung Zusammenhang
zurückgelegte Strecke s überstrichener Winkel φ s=R·φ
Geschwindigkeit v T Winkelgeschwindigkeit ω v T =|v|=R·ω
Beschleunigung a T Winkelbeschleunigung α a T =R·α


Eine weitere wichtige Größe bei Drehbewegungen ist die Frequenz. Sie gibt an, wie oft sich ein Körper in einem Zeitintervall um das Drehzentrum bewegt.
Unter der Drehfrequenz f wird der Quotient zwischen Anzahl der Umdrehungen und der dazu benötigten Zeit Δt verstanden:

f= Umdrehungen Δt  .

In der Technik wird oftmals der Begriff Drehzahl n verwendet. Darunter versteht man die Anzahl der Umdrehungen pro Minute:

n= Umdrehungen Minute  .


Für die Einheiten der Drehfrequenz und der Drehzahl gilt: [f]= 1 s =Hz und [n]= 1 min .
Die Zeit T, die für einen Umlauf benötigt wird, ergibt sich zu:

T= 1 f = 1 n  .

Die Umlaufzeit T ist also der Kehrwert der Drehfrequenz f.


Beispiel 4.5.3  
Sie fahren mit Ihrem Fahrrad. Die Räder drehen sich dabei mit einer Drehzahl von n1 =210· 1/min. Dann werden Sie mit einer konstanten Beschleunigung immer schneller, bis Sie eine Drehzahl von n2 =380· 1/min erreicht haben. Dazu brauchen Sie eine Zeit von t=6,5 s. Die Räder an Ihrem Fahrrad haben einen Radius von R=0,30 m.
Welche Winkelbeschleunigung α erfährt ein Punkt auf dem Rand eines Rades während dieser Zeit und welchen Weg s legt er zurück?
Zur Lösung der Aufgabe betrachtet man zuerst die Winkelgeschwindigkeit. Zu Beginn der Beschleunigung bewegt sich der Punkt mit der Winkelgeschwindigkeit ω1 =2·π· n1 . Das folgt aus den Definitionen der Winkelgeschwindigkeit und der Drehzahl. Nach der Beschleunigung erreicht der Punkt eine Winkelgeschwindigkeit von ω2 =2·π· n2 .
Wie bei der beschleunigten Bewegung werden nun die Bewegungsgesetze aufgestellt. Aus der Gleichung für die Winkelgeschwindigkeit

ω2 = ω1 +α·t

kann dann die Winkelbeschleunigung α bestimmt werden:

α = ω2 - ω1 t = 2·π·( n2 - n1 ) t = 2·π·(380· 1 60 s -210· 1 60 s ) 6,5 s ≈ 2,7  1 s2  .

Für den in der Zeit t überstrichenen Winkel gilt dann:

φ = ω1 ·t+ 1 2 ·α· t2 = ω1 ·t+ 1 2 · ω2 - ω1 t · t2 = 1 2 ·( ω1 + ω2 )·t = 1 2 ·2·π·( n1 + n2 )·t = π·(210· 1 min +380· 1 min )·6,5 s ≈ 200 rad .

Der zurückgelegte Weg s ergibt sich dann durch Multiplikation des Winkels φ mit dem Radius R:

s=φ·R≈60 m .

Zum Vergleich mit der vorhergehenden Aufgabe kann die tangentiale Beschleunigung a T des Fahrrads noch bestimmt werden mit:

a T =R·α≈0,3·2,7  1 s2 =0,81  m s2  .

Es ergibt sich derselbe Wert für die tangentiale Beschleunigung.


Wenn in den folgenden Aufgabentexten nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie g=9,81  m s2  .
Aufgabe 4.5.4  
 
Geben Sie den Winkel α=30 ∘ in Bogenmaß und x= 5 4 π in Grad an.
 
30 ∘  = 
 rad
5 4 π  = 
  ∘
 


Aufgabe 4.5.5  
 
Mit welcher Winkelgeschwindigkeit bewegt sich der Sekundenzeiger einer Uhr, die Erde um die Sonne und der Mond um die Erde?
Nehmen Sie an, dass es sich bei allen Bahnen um Kreisbahnen handelt. Geben Sie das Ergebnis mit drei Stellen an.
 
ω Sekundenzeiger  = 
ω Erde/Sonne  =  E 
ω Mond/Erde  =  E 
 


Aufgabe 4.5.6  
 
Auf einer Kreisscheibe sind zwei Punkte markiert. Die Punkte sollen am Rand der Scheibe und beim halben Radius sitzen. Welche Aussagen treffen zu?
 
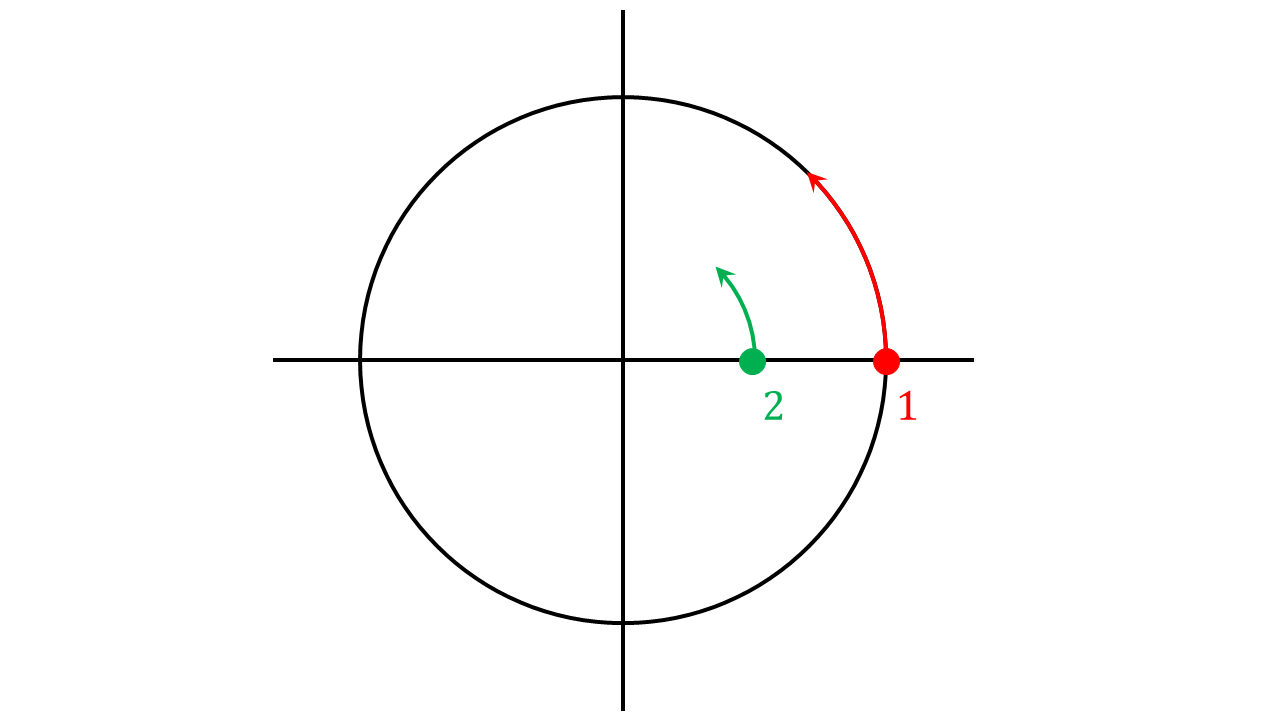
././Physikkurs/drehbewegung_kreisbewegungen/images/Kreisscheibe.png
Abbildung 4.5.3: Skizze (C)


Für die Winkelgeschwindigkeiten der Punkte 1 und 2 gilt:  
Für die Bahngeschwindigkeiten der Punkte 1 und 2 gilt:
 


Aufgabe 4.5.7  
 
Zwei Kinder rollen sich gegenseitig einen Ball zu. Sie sitzen im Abstand von L=5,0 m. Wie groß ist der Radius R des Balls, wenn er auf seinem Weg 8 Umdrehungen macht?
 
Der Radius R des Balles beträgt: R  = 

 


 

Polarkoordinaten (+)


Video 1: Einführung in Polarkoordinaten (C) .

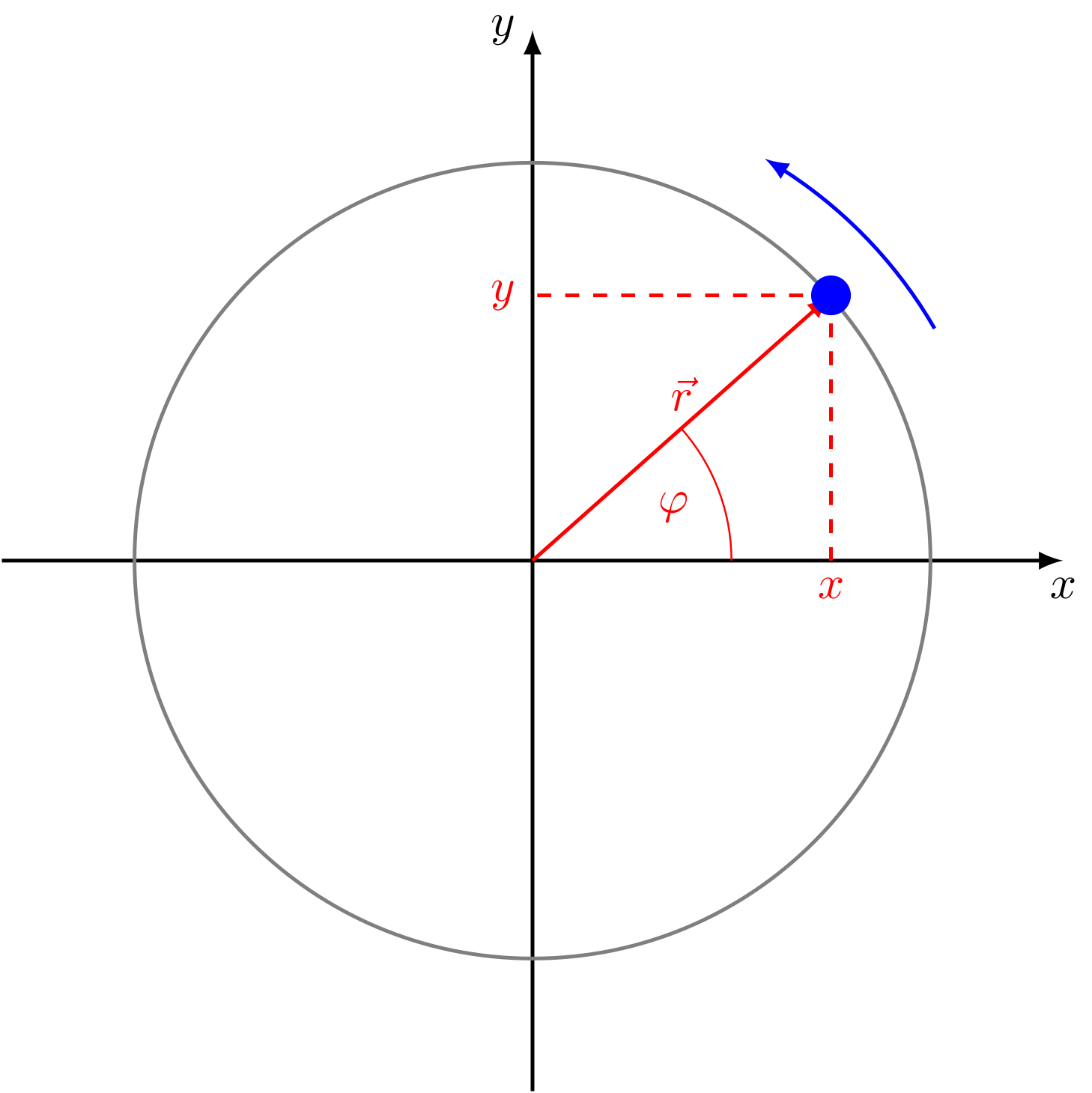
./_EE9C4FD8_4x.png
Abbildung 4.5.4: Polarkoordinaten  (C)

Um später die Kreisbewegungen sinnvoll beschreiben zu können, führen wir zunächst die sogenannten Polarkoordinaten ein. Dies sind Koordinaten in der zweidimensionalen Ebene. Statt der Koordinaten x und y beschreiben dann die beiden Koordinaten r und φ die Lage eines Punktes. Dabei ist r der Radius, also der Abstand des Punktes vom Ursprung des Koordinatensystems. Der Winkel φ ist der sogenannte Azimutalwinkel, der den Winkel zwischen dem Radiusvektor und der x-Achse angibt. Zur Umrechnung von kartesischen Koordinaten in Polarkoordinaten benutzt man folgende Gleichungen:

r = x2 + y2  , φ = arctan y x     für    x>0 .

Falls x<0 ist, muss φ so gewählt werden, dass der richtige Quadrant erreicht wird.

Umgekehrt erhält man für die Umrechnung von Polarkoordinaten in kartesische Koordinaten:

x = rcosφ , y = rsinφ .



Die Polarkoordinaten kann man sich nochmal an folgender Skizze verständlich machen:

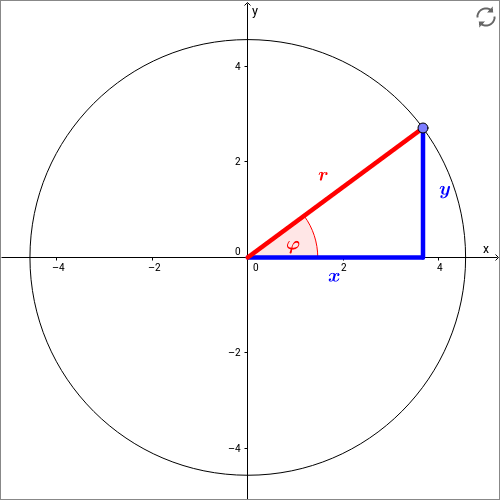
././Physikkurs/drehbewegung_kreisbewegungen/images/geogebra_drehbewegung_standbild1.png
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)

Zur Beschreibung von Kreisbewegungen ist es meistens günstig, wenn man den Ursprung des Koordinatensystems in den Mittelpunkt des Kreises legt.

Video 2: Polarkoordinaten: Beispiel (C) .

Video 3: Polarkoordinaten: Beispiel (C) .



 

Winkelgeschwindigkeit, Umlaufdauer und Frequenz (+)


Video 4: Definition der Winkelgeschwindigkeit (C) .



Die Winkelgeschwindigkeit ω ist die Ableitung des Azimutalwinkels φ nach der Zeit:

ω= dφ dt = φ ·  .



Video 5: Definition von Umlaufdauer und Frequenz (C) .



In gleichförmigen Kreisbewegungen ist die Winkelgeschwindigkeit konstant. Dann gelten folgende Beziehungen zwischen ω, der Umlaufdauer T und der Drehfrequenz f:

ω= 2π T =2πf .



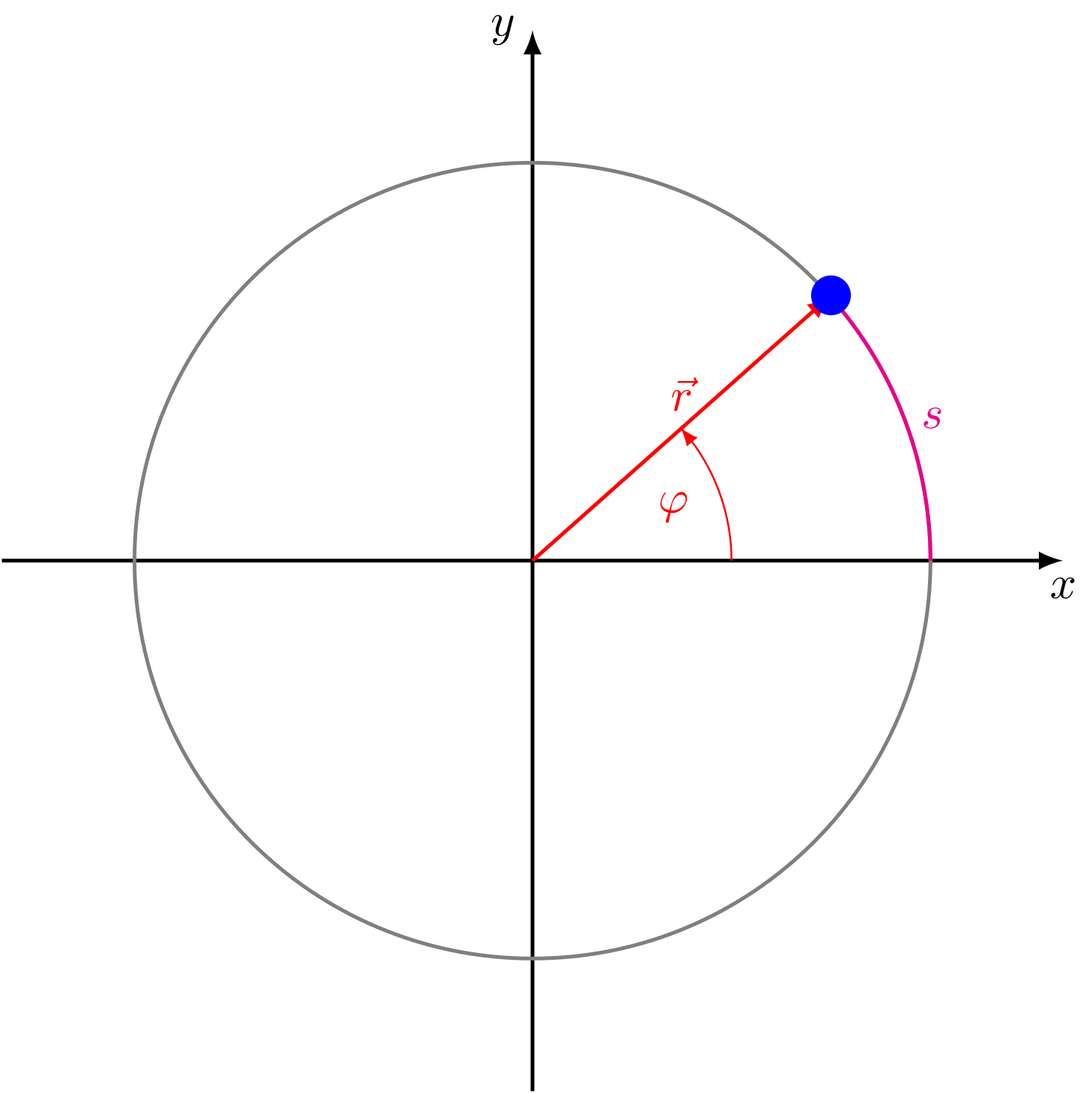
./_5E284850_4x.png
Abbildung 4.5.6: Zusammenhang Azimutalwinkel und Kreisbogen  (C)

Der Azimutalwinkel φ eines Kreissektors kann als Quotient aus dem dazugehörigen Kreisbogen s und dem Radius r der Kreisbahn berechnet werden:

φ= s r  .

Analog erhält man einen Ausdruck für die Winkelgeschwindigkeit ω, indem man beide Seiten der obigen Gleichung nach der Zeit ableitet. Da der Radius r konstant ist, ergibt sich auf der rechten Seite der Quotient zwischen der Geschwindigkeit v auf der Kreisbahn (Bahngeschwindigkeit) und dem Radius r:


ω= v r  .



Video 6: Winkelgeschwindigkeit, Umlaufdauer und Frequenz: Beispiel (C) .



 

Geschwindigkeit und Beschleunigung (+)


Video 7: Definition der Bahngeschwindigkeit (C) .



Bei einer gleichförmigen Kreisbewegung ist die die Bahngeschwindigkeit v konstant, da der Körper in gleichen Zeitintervallen gleiche Strecken auf der Kreisbahn zurücklegt:
 
v= Δs Δt = r Δφ Δt ​ = rω Δt Δt =rω .
 


Video 8: Bahngeschwindigkeit: Beispiel (C) .



Video 9: Vektoreigenschaften der Bahngeschwindigkeit: Ortsvektor (C) .



./_C9BDD0A9_4x.png
Abbildung 4.5.7: Bahngeschwindigkeitsvektor  (C)

Obwohl die Bahngeschwindigkeit v konstant ist, sprechen wir bei der gleichförmigen Kreisbewegung trotzdem von einer beschleunigten Bewegung. Während der Bewegung ändert sich nämlich ständig die Richtung des Geschwindigkeitsvektors. Für den Ortsvektor r → (t) als Funktion der Zeit ergibt sich:

r → (t)=( x(t) y(t) )=( r cos(ωt) r sin(ωt) ) .



Video 10: Vektoreigenschaften der Bahngeschwindigkeit: Geschwindigkeitsvektor (C) .



Um den Geschwindigkeitsvektor v → (t) zu berechnen, bildet man die zeitliche Ableitung von r → (t). Da der Radius r, also der Betrag des Vektors r → , während der Kreisbewegung konstant bleibt, erhält man als Geschwindigkeitsvektor:
 
v → (t)= r → · (t)=( x · (t) y · (t) )​ ​ =( -rω sin(ωt) rω cos(ωt) ) .
 
Der Geschwindigkeitsvektor ändert offenbar mit der Winkelgeschwindigkeit ω der Kreisbewegung seine Richtung. Geschwindigkeitsvektor v → (t) und Ortsvektor r → (t) stehen bei dieser Drehung stets senkrecht aufeinander.

Video 11: Betrag und Richtung des Geschwindigkeitsvektors (C) .

Video 12: Berechnung des Beschleunigungsvektors (Zentripetalbeschleunigung) (C) .



./_DFC15905_4x.png
Abbildung 4.5.8: Orts-, Geschwindigkeits- und Beschleunigungsvektor  (C)

Den Beschleunigungsvektor a → (t) erhält man aus der Ableitung des Geschwindigkeitsvektors v → (t) nach der Zeit:
 
a → (t)= v → · (t)=( v · x (t) v · y (t) )​ ​ =( -r ω2  cos(ωt) -r ω2  sin(ωt) )​ ​ =- ω2 r → (t) .
 


Auch der Beschleunigungsvektor a → (t) dreht sich mit der Winkelgeschwindigkeit ω der Kreisbewegung. Er zeigt immer entgegengesetzt zum Ortsvektor.

Video 13: Betrag und Richtung der Zentripetalbeschleunigung (C) .



Das Verhalten der Vektoren r → (t), v → (t) und a → (t) ist nochmal in der folgenden Skizze illustriert. Sie stellt eine Kreisbewegung mit dem Radius r=1 m und einer Umlaufdauer von T=10 s dar. Starten Sie die Animation und beobachten Sie, wie sich die Vektoren bewegen. Sie ändern mit der Winkelgeschwindigkeit ω ständig ihre Richtung. Ihre Beträge bleiben dabei konstant.

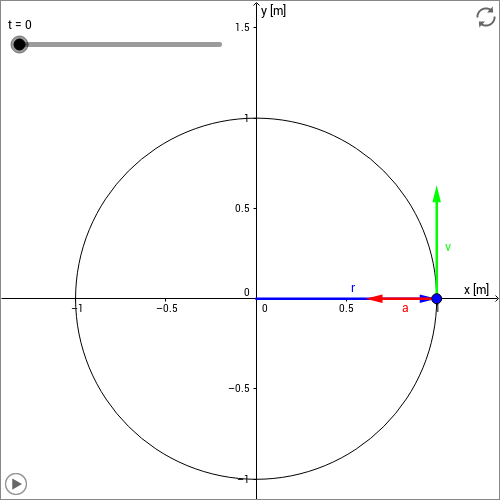
././Physikkurs/drehbewegung_kreisbewegungen/images/geogebra_drehbewegung_standbild2.png
Diese Interaktion wurde mit GeoGebra erstellt (www.geogebra.org)

Die soeben berechnete Beschleunigung a → nennt man die Zentripetalbeschleunigung. Ihr Betrag ar ist gegeben durch:

ar = ω2 ·r= v2 r  .



 

Zentripetal- und Zentrifugalkraft (+)


Video 14: Zentripetalkraft (C) .



./_1D8C78D0_4x.png
Abbildung 4.5.10: Zentripetalbeschleunigung  (C)

Die Zentripetalbeschleunigung ar bewirkt, dass ein Körper auf einer Kreisbewegung zum Mittelpunkt des Kreises hin beschleunigt wird. Um diese Beschleunigung zu erreichen, benötigt man die Zentripetalkraft Fr , mit der man an einem Körper der Masse m ziehen muss, um ihn auf der Kreisbahn zu halten:

 
Fr =m· ar ​ =m· ω2 ·r ​ =m· v2 r  .
 
Wir setzen uns nun in das System des Körpers, vollziehen also die Kreisbewegung mit. In diesem System ruht der Körper, er wird also auch nicht beschleunigt. Daher muss in diesem System eine weitere Kraft auf den Körper wirken, die der Zentripetalkraft F → r entgegen wirkt. Dies ist die Zentrifugalkraft F → Z :

F → Z =- F → r  .



Da diese Kraft nur im mitbewegten System auftritt, spricht man von einer sogenannten Scheinkraft.

Beispiel 4.5.8  


Video 15: Zentripetalkraft: Beispiel (C) .



Mit welcher Kraft muss ein Körper der Masse m=0,1 kg gehalten werden, der zweimal pro Sekunde eine Kreisbahn mit dem Radius r=0,5 m durchläuft? 
Die Zentripetalkraft ist
 
Fr =m ω2 r ​ =m·(2πf )2 ·r ​ =4 π2 ·m f2 r ​ =4 π2 ·0,1 kg· (2  1 s )2 ·0,5 m ​≈7,9 N .
 


Video 16: Zentripetalkraft: Beispiel (C) .




Wenn im Aufgabentext nicht anders angegeben, geben Sie die Ergebnisse auf ganze Zahlen gerundet an. Bei Angaben in wissenschaftlicher Schreibweise (Exponentialschreibweise) runden Sie auf zwei Nachkommastellen.
Falls nicht anders angegeben, verwenden Sie g=9,81  m s2  .